Research Article
Begründung einer strengen Implikation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-128
-
- Article
- Export citation
Recursive functions in basic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 337-346
-
- Article
- Export citation
Identity, variables, and impredicative definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 225-245
-
- Article
- Export citation
A new approach to semantics – Part I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-27
-
- Article
- Export citation
On the definition of ‘formal deduction’1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 129-136
-
- Article
- Export citation
On ω-consistency and related properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 246-252
-
- Article
- Export citation
Two concepts from the theory of models1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 28-32
-
- Article
- Export citation
Alternative postulate sets for Lewis's S5
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 347-349
-
- Article
- Export citation
The independence of a weak axiom of choice1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 350-366
-
- Article
- Export citation
On simplifying truth-functional formulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 253-254
-
- Article
- Export citation
On the interpretation of Aristotelian syllogistic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 137-147
-
- Article
- Export citation
Note on a problem of L. Henkin
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-35
-
- Article
- Export citation
On formulas with valid cases
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 148
-
- Article
- Export citation
Independent axiom schemata for S5
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 255-256
-
- Article
- Export citation
Reviews
A. Heyting. Intuitionism. An introduction. Studies in logic and the foundations of mathematics. North-Holland Publishing Company, Amsterdam1956, VIII + 133 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 367-371
-
- Article
- Export citation
Research Article
On the axiom of extensionality – Part I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 36-48
-
- Article
- Export citation
Solution of a problem of Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-51
-
- Article
- Export citation
Reviews
B. Ú. Pil'čak. Ob isčislénii zadač (On the calculus of problems). Ukrainskij matématičéskij žurnal, vol. 4 (1952), pp. 174–194.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 372
-
- Article
- Export citation
Research Article
The representations of S5
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 257-260
-
- Article
- Export citation
A new approach to semantics – Part II1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 149-161
-
- Article
- Export citation



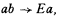
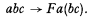
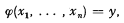
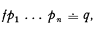
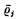 of
of 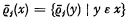 .
.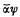 as in [5], but allowing
as in [5], but allowing 

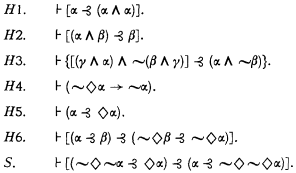
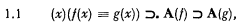
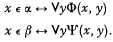
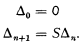
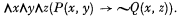

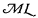 the system of VI 112 without axioms C4 and
the system of VI 112 without axioms C4 and 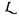 as having Zermelo set theory, without the axiom of infinity, as its logical basis – but it must be kept in mind that this is not an essential feature of the forthcoming definitions.
as having Zermelo set theory, without the axiom of infinity, as its logical basis – but it must be kept in mind that this is not an essential feature of the forthcoming definitions.