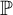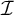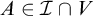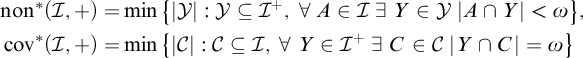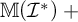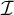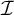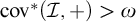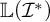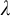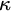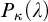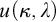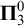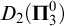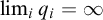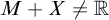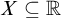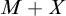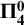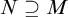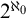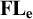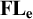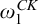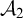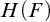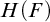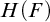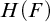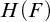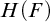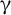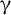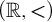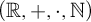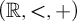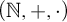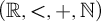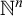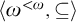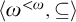Article
FORCING CONSTRUCTIONS AND COUNTABLE BOREL EQUIVALENCE RELATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2022, pp. 873-893
-
- Article
- Export citation
COMPLEXITY OF INDEX SETS OF DESCRIPTIVE SET-THEORETIC NOTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2022, pp. 894-911
-
- Article
- Export citation
NEW RELATIONS AND SEPARATIONS OF CONJECTURES ABOUT INCOMPLETENESS IN THE FINITE DOMAIN
- Part of:
-
- Published online by Cambridge University Press:
- 22 November 2021, pp. 912-937
-
- Article
- Export citation
WAYS OF DESTRUCTION
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2021, pp. 938-966
-
- Article
- Export citation
APPLICATIONS OF PCF THEORY TO THE STUDY OF IDEALS ON
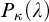
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2022, pp. 967-994
-
- Article
- Export citation
COMPLETE INTUITIONISTIC TEMPORAL LOGICS FOR TOPOLOGICAL DYNAMICS
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2022, pp. 995-1022
-
- Article
- Export citation
DESCRIPTIVE COMPLEXITY IN CANTOR SERIES
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1023-1045
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MEAGER-ADDITIVE SETS IN TOPOLOGICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1046-1064
-
- Article
- Export citation
YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1065-1092
-
- Article
- Export citation
ALMOST DISJOINT AND MAD FAMILIES IN VECTOR SPACES AND CHOICE PRINCIPLES
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1093-1110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUBCOMPACT CARDINALS, TYPE OMISSION, AND LADDER SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1111-1129
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING SIBLINGS IN UNIVERSAL THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1130-1155
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MOST SIMPLE EXTENSIONS OF
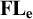 $\textbf{FL}_{\textbf{e}}$
ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$
ARE UNDECIDABLE
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
-
- Article
- Export citation
COPYING ONE OF A PAIR OF STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1201-1214
-
- Article
- Export citation
INTERPRETING A FIELD IN ITS HEISENBERG GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2021, pp. 1215-1230
-
- Article
- Export citation
NULL SETS AND COMBINATORIAL COVERING PROPERTIES
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1231-1242
-
- Article
- Export citation
CONNECTEDNESS IN STRUCTURES ON THE REAL NUMBERS: O-MINIMALITY AND UNDECIDABILITY
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1243-1259
-
- Article
- Export citation
INITIAL SEGMENTS OF THE DEGREES OF CEERS
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1260-1282
-
- Article
- Export citation
FIRST-ORDER AXIOMATISATIONS OF REPRESENTABLE RELATION ALGEBRAS NEED FORMULAS OF UNBOUNDED QUANTIFIER DEPTH
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2021, pp. 1283-1300
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 87 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. f1-f3
-
- Article
-
- You have access
- Export citation