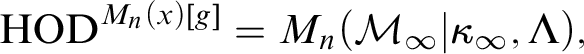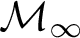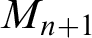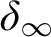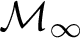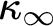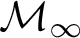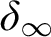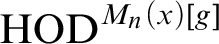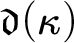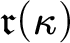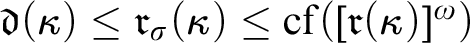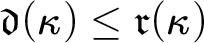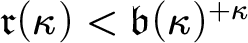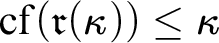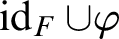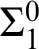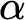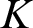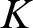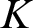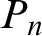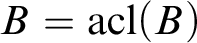Article
 $\operatorname {HOD}$
IN INNER MODELS WITH WOODIN CARDINALS
$\operatorname {HOD}$
IN INNER MODELS WITH WOODIN CARDINALS
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2021, pp. 871-896
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ZFC INEQUALITIES BETWEEN CARDINAL INVARIANTS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2021, pp. 897-912
-
- Article
- Export citation
FRAÏSSÉ LIMITS FOR RELATIONAL METRIC STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2021, pp. 913-934
-
- Article
- Export citation
THE POSET OF ALL LOGICS I: INTERPRETATIONS AND LATTICE STRUCTURE
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2021, pp. 935-964
-
- Article
- Export citation
SYMÉTRIES ET TRANSVEXIONS, PRINCIPALEMENT DANS LES GROUPES DE RANG DE MORLEY FINI SANS INVOLUTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2021, pp. 965-990
-
- Article
- Export citation
VAUGHT’S CONJECTURE FOR ALMOST CHAINABLE THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2021, pp. 991-1005
-
- Article
- Export citation
MÜNCHHAUSEN PROVABILITY
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1006-1034
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
-
- Article
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
-
- Article
- Export citation
NOTES ON SOME ERDŐS–HAJNAL PROBLEMS
- Part of:
-
- Published online by Cambridge University Press:
- 12 August 2021, pp. 1116-1123
-
- Article
- Export citation
PRENEX NORMAL FORM THEOREMS IN SEMI-CLASSICAL ARITHMETIC
- Part of:
-
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1124-1153
-
- Article
-
- You have access
- HTML
- Export citation
ORDINAL ANALYSIS OF PARTIAL COMBINATORY ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1154-1188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FIBRED ALGEBRAIC SEMANTICS FOR A VARIETY OF NON-CLASSICAL FIRST-ORDER LOGICS AND TOPOLOGICAL LOGICAL TRANSLATION
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1189-1213
-
- Article
- Export citation
COUNTABLY PERFECTLY MEAGER SETS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2021, pp. 1214-1227
-
- Article
- Export citation
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
-
- Article
- Export citation
WEAK CANONICAL BASES IN NSOP
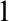 $_1$
THEORIES
$_1$
THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 11 June 2021, pp. 1259-1281
-
- Article
- Export citation
ON SUPERSETS OF NON-LOW
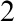 $_2$
SETS
$_2$
SETS
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1282-1292
-
- Article
- Export citation
ASSOCIATIVITY OF THE MORLEY PRODUCT OF INVARIANT MEASURES IN NIP THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 12 August 2021, pp. 1293-1300
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 86 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 December 2021, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JSL volume 86 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 December 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation