Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T09:50:57.267Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAKLY REMARKABLE CARDINALS, ERDŐS CARDINALS, AND THE GENERIC VOPĚNKA PRINCIPLE

Published online by Cambridge University Press:  13 September 2019

TREVOR M. WILSON
TREVOR M. WILSON*
Affiliation:
DEPARTMENT OF MATHEMATICS MIAMI UNIVERSITY OXFORD, OHIO45056, USA E-mail: twilson@miamioh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a weak version of Schindler’s remarkable cardinals that may fail to be 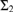${{\rm{\Sigma }}_2}$-reflecting. We show that the 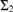${{\rm{\Sigma }}_2}$-reflecting weakly remarkable cardinals are exactly the remarkable cardinals, and that the existence of a non-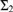${{\rm{\Sigma }}_2}$-reflecting weakly remarkable cardinal has higher consistency strength: it is equiconsistent with the existence of an ω-Erdős cardinal. We give an application involving gVP, the generic Vopěnka principle defined by Bagaria, Gitman, and Schindler. 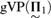Namely, we show that gVP + “Ord is not ${{\rm{\Delta }}_2}$-Mahlo” and ${\text{gVP}}(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{\Pi } _1 )$ + “there is no proper class of remarkable cardinals” are both equiconsistent with the existence of a proper class of ω-Erdős cardinals, extending results of Bagaria, Gitman, Hamkins, and Schindler.

Keywords

03E55virtual large cardinalsremarkable cardinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1711 - 1721
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., $C^{\left( n \right)} $-cardinals. Archive for Mathematical Logic, vol. 51 (2012), no. 3–4, pp. 213–240.CrossRefGoogle Scholar
Bagaria, J., Gitman, V., and Schindler, R., Generic Vopěnka’s Principle, remarkable cardinals, and the weak Proper Forcing Axiom. Archive for Mathematical Logic, vol. 56 (2017), no. 1–2, pp. 1–20.CrossRefGoogle Scholar
Baumgartner, J. E., Ineffability properties of cardinals II, Logic, Foundations of Mathematics, and Computability Theory (Butts, R. E. and Hintikka, J., editors), D. Reidel Publishing Company, Dordrecht, 1977, pp. 87–106.CrossRefGoogle Scholar
Gitman, V., Ramsey-like cardinals, this Journal, vol. 76 (2011), no. 2, pp. 519–540.Google Scholar
Gitman, V. and Hamkins, J. D., A model of the generic Vopěnka principle in which the ordinals are not Mahlo. Archive for Mathematical Logic, vol. 58 (2019), no. 1–2, pp. 245–265.CrossRefGoogle Scholar
Gitman, V. and Schindler, R., Virtual large cardinals. Annals of Pure and Applied Logic, vol. 169 (2018), no. 12, pp. 1317–1334.CrossRefGoogle Scholar
Gitman, V. and Welch, P. D., Ramsey-like cardinals II, this Journal, vol. 76 (2011), no. 2, pp. 541–560.Google Scholar
Magidor, M., On the role of supercompact and extendible cardinals in logic. Israel Journal of Mathematics, vol. 10 (1971), no. 2, pp. 147–157.CrossRefGoogle Scholar
Schindler, R.-D., Proper forcing and remarkable cardinals. The Bulletin of Symbolic Logic, vol. 6 (2000), no. 02, pp. 176–184.CrossRefGoogle Scholar
Schindler, R.-D., Proper forcing and remarkable cardinals II, this Journal, vol. 66 (2001), no. 3, pp. 1481–1492.Google Scholar
Schmerl, J. H., On κ-like structures which embed stationary and closed unbounded subsets. Annals of Mathematical Logic, vol. 10 (1976), no. 3, pp. 289–314.CrossRefGoogle Scholar
Silver, J. H., A large cardinal in the constructible universe. Fundamenta Mathematicae, vol. 69 (1970), pp. 93–100.CrossRefGoogle Scholar
Solovay, R. M., Reinhardt, W. N., and Kanamori, A., Strong axioms of infinity and elementary embeddings. Annals of Mathematical Logic, vol. 13 (1978), no. 1, pp. 73–116.CrossRefGoogle Scholar