Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-20T12:47:04.355Z Has data issue: false hasContentIssue false
  • English
  • Français

A VALUATION THEORETIC CHARACTERIZATION OF RECURSIVELY SATURATED REAL CLOSED FIELDS

Published online by Cambridge University Press:  13 March 2015

PAOLA D’AQUINO ,
SALMA KUHLMANN  and
KAREN LANGE
PAOLA D’AQUINO
Affiliation:
DIPARTIMENTO DI MATEMATICA, SECONDA UNIVERSITÀ DI NAPOLI, ITALYE-mail: paola.daquino@unina2.it
SALMA KUHLMANN
Affiliation:
FB MATHEMATIK & STATISTIK, UNIVERSITÄT KONSTANZ, GERMANYE-mail: salma.kuhlmann@uni-konstanz.de
KAREN LANGE
Affiliation:
DEPARTMENT OF MATHEMATICS, WELLESLEY COLLEGE, UNITED STATESE-mail:karen.lange@wellesley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a valuation theoretic characterization for a real closed field to be recursively saturated. This builds on work in [9], where the authors gave such a characterization for κ-saturation, for a cardinal 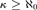$\kappa \ge \aleph _0 $. Our result extends the characterization of Harnik and Ressayre [7] for a divisible ordered abelian group to be recursively saturated.

Keywords

Recursive saturationScott setsnatural valuationvalue groupresidue fieldvaluation rankpseudo-Cauchy sequences
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 194 - 206
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alling, N. L. and Kuhlmann, S., On $\eta _\alpha $-groups and fields. Order, vol. 11 (1994), pp. 85–92.CrossRefGoogle Scholar
Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
Brown, R., Valued vector spaces of countable dimension. Publicationes Mathematicae Debrecen. vol. 18 (1971), pp. 149–151.Google Scholar
D’Aquino, P., Knight, J.F., and Starchenko, S., Real closed fields and models of Peano arithmetic, this Journal, vol. 75 (2010), no. 1, pp. 1–11.Google Scholar
Engler, A. J. and Prestel, A., Valued Fields, Springer, Berlin, 2005.Google Scholar
Harnik, V.,ω 1-Like recursively saturated models of Presburger’s Arithmetic, this Journal, vol. 51 (1986), no. 2, pp. 421–429.Google Scholar
Harnik, V. and Ressayre, J.P., Draft of a paper, 1992.Google Scholar
Kuhlmann, F.-V., Value groups, residue fields and bad places of rational function fields.Transactions of the American Mathematical Society, vol. 356 (2004), pp. 4559–4600.CrossRefGoogle Scholar
Kuhlmann, F.-V., Kuhlmann, S., Marshall, M., and Zekavat, M., Embedding ordered fields in formal power series fields. Journal of Pure and Applied Algebra, vol. 169 (2002), pp. 71–90.Google Scholar
Kuhlmann, S., Groupes abéliens divisibles ordonnés Séminaire sur les Structures Algébriques Ordonnées, Sélection d’exposés 1984-1987, vol. 1 (1990), pp. 3–14.Google Scholar
Kuhlmann, S., Ordered Exponential Fields, The Fields Institute Monograph Series, vol. 12, American Mathematical Society, Providence, R.I., 2000.Google Scholar
Knight, J. and Nadel, M., Models of Peano Arithemetic and closed ideals, this Journal, vol. 47 (1982), no. 4, pp. 833–840.Google Scholar
Macintyre, A. and Marker, D., Degrees of recursively saturated models. Transactions of the American Mathematical Society, vol. 282 (1984), pp. 539–554.Google Scholar
Marker, D., Personal communication, 2013.Google Scholar
Rosenstein, J.G., Linear Orderings, Academic Press, New York, NY, 1982.Google Scholar
Samuel, P. and Zariski, O., Commutative Algebra, Graduate Texts in Mathematics, vol. 2, Springer, Berlin, 1960.Google Scholar
Scott, D., Algebra of sets binumerable in complete extensions of arithmetic, Recursive Functions Theory (Dekker, J., editor), American Mathematical Society, Providence, R.I., 1962, pp. 117–121.Google Scholar