Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-02T23:46:16.762Z Has data issue: false hasContentIssue false
  • English
  • Français

THREE SURPRISING INSTANCES OF DIVIDING

Part of: Model theory

Published online by Cambridge University Press:  21 March 2024

GABRIEL CONANT  and
ALEX KRUCKMAN
GABRIEL CONANT
Affiliation:
DEPARTMENT OF MATHEMATICS THE OHIO STATE UNIVERSITY COLUMBUS, OH 43210 USA E-mail: conant.38@osu.edu
ALEX KRUCKMAN*
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE WESLEYAN UNIVERSITY MIDDLETOWN, CT 06459 USA
*
E-mail: akruckman@wesleyan.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give three counterexamples to the folklore claim that in an arbitrary theory, if a complete type p over a set B does not divide over 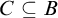$C\subseteq B$, then no extension of p to a complete type over 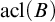$\operatorname {acl}(B)$ divides over C. Two of our examples are also the first known theories where all sets are extension bases for nonforking, but forking and dividing differ for complete types (answering a question of Adler). One example is an 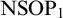$\mathrm {NSOP}_1$ theory with a complete type that forks, but does not divide, over a model (answering a question of d’Elbée). Moreover, dividing independence fails to imply M-independence in this example (which refutes another folklore claim). In addition to these counterexamples, we summarize various related properties of dividing that are still true. We also address consequences for previous literature, including an earlier unpublished result about forking and dividing in free amalgamation theories, and some claims about dividing in the theory of generic 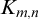$K_{m,n}$-free incidence structures.

Keywords

forking and dividingindependence relationsalgebraic closurefree amalgamation theories

MSC classification

Primary: 03C45: Classification theory, stability and related concepts
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., Explanation of independence, Ph.D. thesis, Albert-Ludwigs-Universität Freiburg, 2005.Google Scholar
Adler, H., Around pregeometric theories, unpublished notes, 2007.Google Scholar
Adler, H., A geometric introduction to forking and thorn-forking . Journal of Mathematical Logic, vol. 9 (2009), no. 1, pp. 1–20.CrossRefGoogle Scholar
Casanovas, E., Simple Theories and Hyperimaginaries, Lecture Notes in Logic, 39, Association for Symbolic Logic, Chicago, 2011.CrossRefGoogle Scholar
Cherlin, G., Shelah, S., and Shi, N., Universal graphs with forbidden subgraphs and algebraic closure , Advances in Applied Mathematics, vol. 22 (1999), no. 4, pp. 454–491.CrossRefGoogle Scholar
Chernikov, A. and Kaplan, I., Forking and dividing in $\mathrm{NTP}_2$ theories, this Journal, vol. 77 (2012), no. 1, pp. 1–20.2012 Google Scholar
Conant, G., An axiomatic approach to free amalgamation, this Journal, vol. 82 (2017), no. 2, pp. 648–671.2017 Google Scholar
Conant, G., Forking and dividing in Henson graphs . Notre Dame Journal of Formal Logic, vol. 58 (2017), no. 4, pp. 555–566.CrossRefGoogle Scholar
Conant, G. and Hanson, J., Separation for isometric group actions and hyperimaginary independence . Fundamenta Mathematicae, vol. 259 (2022), no. 1, pp. 97–109.CrossRefGoogle Scholar
Conant, G. and Kruckman, A., Independence in generic incidence structures, this Journal, vol. 84 (2019), no. 2, pp. 750–780.2019 Google Scholar
d’Elbée, C., Generic expansions by a reduct . Journal of Mathematical Logic, vol. 21 (2021), no. 3, Article no. 2150016, 44 pp.CrossRefGoogle Scholar
d’Elbée, C., Forking, imaginaries, and other features of $\mathrm{ACFG}$ , this Journal, vol. 86 (2021), no. 2, pp. 669–700.2021 Google Scholar
d’Elbée, C., Axiomatic theory of independence relations in model theory, preprint, 2023, arXiv:2308.07064.Google Scholar
d’Elbée, C., Note on a bomb dropped by Mr Conant and Mr Kruckman, and its consequences for the theory ACFG, preprint, 2023, arXiv:2311.02208.Google Scholar
Dobrowolski, J., Kim, B., and Ramsey, N., Independence over arbitrary sets in $NSO{P}_1$ theories . Annals of Pure and Applied Logic, vol. 173 (2022), no. 2, Article no. 103058, 20 pp.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Kaplan, I. and Ramsey, N., On Kim-independence . Journal of the European Mathematical Society (JEMS), vol. 22 (2020), no. 5, pp. 1423–1474.CrossRefGoogle Scholar
Kruckman, A., How to show that an algebraic formula divides?, Mathematics Stack Exchange, 2019, https://math.stackexchange.com/q/3349094 (version: 2019-09-10).Google Scholar
Kruckman, A., Independence and algebraic closure for stable theories, Mathematics Stack Exchange, 2021, https://math.stackexchange.com/q/4120234 (version: 2021-08-02).Google Scholar
Kruckman, A. and Ramsey, N., Generic expansion and Skolemization in $\mathrm{NSOP}_1$ theories . Annals of Pure and Applied Logic, vol. 169 (2018), no. 8, pp. 755–774.CrossRefGoogle Scholar
Mutchnik, S., Conant-independence and generalized free amalgamation, preprint, 2022, arXiv:2210.07527.Google Scholar
Patel, R., A family of countably universal graphs without SOP ${}_4$ , preprint, 2006.Google Scholar
Shelah, S., Toward classifying unstable theories . Annals of Pure and Applied Logic, vol. 80 (1996), no. 3, pp. 229–255.CrossRefGoogle Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, 40, Association for Symbolic Logic, La Jolla, 2012.CrossRefGoogle Scholar