Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T09:57:22.977Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONG COMPACTNESS, SQUARE, GCH, AND WOODIN CARDINALS

Part of: Set theory

Published online by Cambridge University Press:  26 August 2022

ARTHUR W. APTER
ARTHUR W. APTER*
Affiliation:
DEPARTMENT OF MATHEMATICS BARUCH COLLEGE OF CUNY NEW YORK, NY 10010, USA and DEPARTMENT OF MATHEMATICS THE CUNY GRADUATE CENTER, 365 FIFTH AVENUE NEW YORK, NY 10016, USA URL: http://faculty.baruch.cuny.edu/aapter
*
E-mail: awapter@alum.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show the consistency, relative to the appropriate supercompactness or strong compactness assumptions, of the existence of a non-supercompact strongly compact cardinal 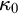$\kappa _0$ (the least measurable cardinal) exhibiting properties which are impossible when 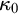$\kappa _0$ is supercompact. 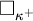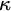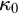In particular, we construct models in which $\square _{\kappa ^+}$ holds for every inaccessible cardinal $\kappa $ except $\kappa _0$ , GCH fails at every inaccessible cardinal except 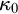$\kappa _0$ , and 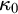$\kappa _0$ is less than the least Woodin cardinal.

Keywords

supercompact cardinalstrongly compact cardinalWoodin cardinalsquare

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E55: Large cardinals
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apter, A., Diamond, square, and level by level equivalence . Archive for Mathematical Logic , vol. 44 (2005), pp. 387–395.CrossRefGoogle Scholar
Apter, A., Inaccessible cardinals, failures of GCH, and level by level equivalence . Notre Dame Journal of Formal Logic , vol. 55 (2014), pp. 431–444.CrossRefGoogle Scholar
Apter, A. and Cummings, J., Identity crises and strong compactness, this Journal, vol. 65 (2000), pp. 1895–1910.Google Scholar
Cummings, J., Foreman, M., and Magidor, M., Squares, scales, and stationary reflection . Journal of Mathematical Logic , vol. 1 (2001), pp. 35–98.CrossRefGoogle Scholar
Hamkins, J. D., Gap forcing: Generalizing the Lévy–Solovay theorem . The Bulletin of Symbolic Logic , vol. 5 (1999), pp. 264–272.CrossRefGoogle Scholar
Hamkins, J. D., Gap forcing . Israel Journal of Mathematics , vol. 125 (2001), pp. 237–252.CrossRefGoogle Scholar
Hamkins, J. D. and Woodin, W. H., Small forcing creates neither strong nor Woodin cardinals . Proceedings of the American Mathematical Society , vol. 128 (2000), pp. 3025–3029.CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite , Springer, Berlin and New York, 1994, 2003, and 2009.Google Scholar
Lévy, A. and Solovay, R., Measurable cardinals and the continuum hypothesis . Israel Journal of Mathematics , vol. 5 (1967), pp. 234–248.CrossRefGoogle Scholar
Magidor, M., How large is the first strongly compact cardinal? Or a study on identity crises . Annals of Mathematical Logic , vol. 10 (1976), pp. 33–57.CrossRefGoogle Scholar
Schimmerling, E., A core model toolbox and guide , Handbook of Set Theory (M. Foreman and A. Kanamori, editors), Springer, Berlin and New York, 2010, pp. 1685–1751.CrossRefGoogle Scholar
Schimmerling, E. and Zeman, M., Square in core models. The Bulletin of Symbolic Logic , vol. 7 (2001), pp. 305–314.CrossRefGoogle Scholar
Solovay, R., Strongly compact cardinals and the GCH , Proceedings of the Tarski Symposium (L. Henkin, J. Addison, C. C. Chang, W. Craig, D. Scott, and R. Vaught, editors), Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, 1974, pp. 365–372.CrossRefGoogle Scholar
Solovay, R., Reinhardt, W., and Kanamori, A., Strong axioms of infinity and elementary Embeddings . Annals of Mathematical Logic , vol. 13 (1978), pp. 73–116.CrossRefGoogle Scholar