Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T19:55:53.076Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRENGTH OF RAMSEY’S THEOREM FOR COLORING RELATIVELY LARGE SETS

Published online by Cambridge University Press:  17 April 2014

LORENZO CARLUCCI  and
KONRAD ZDANOWSKI
LORENZO CARLUCCI
Affiliation:
DIPARTIMENTO DI INFORMATICA, UNIVERSITY OF ROME I “LA SAPIENZA” ROME, ITALYE-mail:carlucci@di.uniroma1.it
KONRAD ZDANOWSKI
Affiliation:
UNIVERSITY OF CARDINAL STEFAN WYSZYŃSKI, WARSAW, POLANDE-mail:k.zdanowski@uksw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize the effective content and the proof-theoretic strength of a Ramsey-type theorem for bi-colorings of so-called exactly large sets. An exactly large set is a set 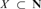$X \subset {\bf{N}}$ such that 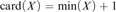${\rm{card}}\left( X \right) = {\rm{min}}\left( X \right) + 1$. The theorem we analyze is as follows. For every infinite subset M of N, for every coloring C of the exactly large subsets of M in two colors, there exists and infinite subset L of M such that C is constant on all exactly large subsets of L. This theorem is essentially due to Pudlák and Rödl and independently to Farmaki. We prove that—over RCA0 —this theorem is equivalent to closure under the ωth Turing jump (i.e., under arithmetical truth). Natural combinatorial theorems at this level of complexity are rare. In terms of Reverse Mathematics we give the first Ramsey-theoretic characterization of 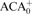${\rm{ACA}}_0^ +$. Our results give a complete characterization of the theorem from the point of view of Computability Theory and of the Proof Theory of Arithmetic. This nicely extends the current knowledge about the strength of Ramsey’s Theorem. We also show that analogous results hold for a related principle based on the Regressive Ramsey’s Theorem. We conjecture that analogous results hold for larger ordinals.

Keywords

Ramsey’s Theoremrelatively large setstrue arithmetic
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 1 , March 2014 , pp. 89 - 102
Copyright
Copyright © Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alspach, D. and Argyros, S., Complexity of weakly null sequences. Dissertationes Mathematicae, vol. 321 (1992), pp. 1–44.Google Scholar
Alspach, D. and Odell, E., Averaging weakly null sequences, Lecture Notes in Mathematics, vol. 1332, Springer, Berlin, 1988, pp. 126–144.Google Scholar
Carlucci, L., Lee, G., and Weiermann, A., Sharp thresholds for hypergraph regressive Ramsey numbers. Journal of Combinatorial Theory, Series A, vol. 118 (2011), no. 2, pp. 558–585.CrossRefGoogle Scholar
Carlucci, L. and Zdanowski, K., A note on Ramsey Theorems and Turing Jumps, How the World Computes - Turing Centenary Conference and 8th Conference on Computability in Europe (Cooper, S. Barry, Dawar, Anuj, and Löwe, Benedikt, editors), CiE 2012, Cambridge, UK, June 18–23, 2012. Proceedings, Lecture Notes in Computer Science 7318, pp. 89–95.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
De Smet, M., Unprovability and phase transitions in Ramsey theory, Ph.D. thesis, University of Ghent, 2011.Google Scholar
Dzhafarov, D. D. and Hirst, J. L., The polarized Ramsey’s theorem. Archive for Mathematical Logic, vol. 48 (2011), no. 2, pp. 141–157.CrossRefGoogle Scholar
Enderton, H. B. and Putnam, H., A note on the hyperarithmetical hierarchy, this Journal, vol. 35 (1970), no. 3, pp. 429–430.Google Scholar
Farmaki, V. and Negrepontis, S., Schreier sets in Ramsey theory. Transactions of the American Mathematical Society, vol. 360 (2008), no. 2, pp. 849–880.Google Scholar
Graham, R. L., Rothschild, B. L., and Spencer, J. H., Ramsey theory. Wiley, New York, 1990.Google Scholar
Jockusch, C. G., Ramsey’s theorem and recursion theory, this Journal, vol. 37 (1972),pp. 268–280.Google Scholar
Kanamori, A. and McAloon, K., On Gödel incompleteness and finite combinatorics. Annals of Pure and Applied Logic, vol. 33 (1987), no. 1, pp. 23–41.CrossRefGoogle Scholar
Ketonen, J. and Solovay, R., Rapidly growing Ramsey functions. Annals of Mathematics, Series 2, vol. 113 (1981), pp. 267–314.Google Scholar
Kojman, M. and Shelah, S., Regressive Ramsey numbers are Ackermannian. Journal of Combinatorial Theory, Series A, vol. 86 (1999), no. 1, pp. 177–181.CrossRefGoogle Scholar
Kojman, M., Lee, G., Omri, E., and Weiermann, A., Sharp thresholds for the phase transition between primitive recursive and Ackermannian Ramsey numbers. Journal of Combinatorial Theory, Series A, vol. 115 (2008), no. 6, pp. 1036–1055.Google Scholar
Marcone, A. and Montalbàn, A., The Veblen function for computability theorists, this Journal, vol. 76 (2011), no. 2, pp. 575–602.Google Scholar
McAloon, K., Paris-Harrington incompleteness and transfinite progressions of theories. Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, 1985, pp. 447–460.Google Scholar
Mileti, J., The canonical Ramsey’s theorem and computability theory. Transactions of the American Mathematical Society, vol. 160 (2008), pp. 1309–1340.Google Scholar
Paris, J. and Harrington, L., A mathematical incompleteness in Peano Arithmetic, Handbook of mathematical logic, (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 1133–1142.Google Scholar
Pudlák, P. and Rödl, V., Partition theorems for systems of finite subsets of integers. Discrete Mathematics, vol. 39 (1982), no. 1, pp. 67–73.Google Scholar
Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967. Reprinted by MIT Press, Cambridge, MA, 1987.Google Scholar
Shoenfield, J. T., On degrees of unsolvability. The Annals of Mathematics, Second Series, vol. 69 (1959), no. 3, pp. 644–653.CrossRefGoogle Scholar
Schreier, J., Ein Gegenbeispiel zur Theorie der schwachen Konvergenz. Studia Mathematica, vol. 2 (1930), pp. 58–62.Google Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem. Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582.Google Scholar
Simpson, S. G., Subsystems of second order arithmetic, Springer-Verlag, Berlin, 1999.CrossRefGoogle Scholar
Soare, R., Computably enumerable sets and degrees, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
Tomczak-Jaegermann, N., Banach spaces of type p have arbitrarily distortable subspaces. Geometric and Functional Analysis, vol. 6 (1996), no. 6, pp. 1074–1082.Google Scholar