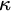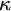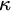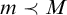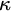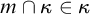1 Set theory with urelements
Set theory was traditionally often conceived as a theory of abstract collection taking place over a class of already-existing primitive objects, the urelements or atoms—we use the terms interchangeably—the irreducible mathematical objects, which are not sets but out of which the sets are to be formed. Perhaps we have numbers as these primitive urelements, or perhaps geometric points or some other kind of atomic, irreducible mathematical object. With these urelement atoms in hand, we proceed to form the sets of atoms, sets of sets of atoms, and so on. The cumulative set-theoretic universe thus grows out of the atoms.

So let us consider this urelement set theory. If A is the class of all urelement atoms, we denote the corresponding set-theoretic universe by
![]() $V(A)$
, reserving the symbol V to denote the class of pure sets, which have no urelements amongst their hereditary members; we do not intend to suggest with this notation that
$V(A)$
, reserving the symbol V to denote the class of pure sets, which have no urelements amongst their hereditary members; we do not intend to suggest with this notation that
![]() $V(A)$
was somehow constructed from V by adding urelements A, although we shall explain (page 3) senses in which
$V(A)$
was somehow constructed from V by adding urelements A, although we shall explain (page 3) senses in which
![]() $V(A)$
does admit a cumulative hierarchical structure. Rather, the central structure in focus is
$V(A)$
does admit a cumulative hierarchical structure. Rather, the central structure in focus is
![]() ${\left \langle V(A),\in ,{\mathbb A}\right \rangle }$
, a model of the theory we shall presently describe, where
${\left \langle V(A),\in ,{\mathbb A}\right \rangle }$
, a model of the theory we shall presently describe, where
![]() $V(A)$
denotes the class of all sets and atoms and
$V(A)$
denotes the class of all sets and atoms and
![]() ${\mathbb A}$
is a predicate picking out the atoms, so that
${\mathbb A}$
is a predicate picking out the atoms, so that
![]() ${\mathbb A}(a)$
holds exactly when a is an urelement atom. This predicate distinguishes the urelements from the empty set
${\mathbb A}(a)$
holds exactly when a is an urelement atom. This predicate distinguishes the urelements from the empty set
![]() $\varnothing $
, which would otherwise appear like an urelement in having no elements, but amongst these
$\varnothing $
, which would otherwise appear like an urelement in having no elements, but amongst these
![]() $\in $
-minimal objects, only
$\in $
-minimal objects, only
![]() $\varnothing $
is a set. The predicate
$\varnothing $
is a set. The predicate
![]() ${\mathbb A}$
is thus definable in
${\mathbb A}$
is thus definable in
![]() ${\left \langle V(A),\in \right \rangle }$
from the parameter
${\left \langle V(A),\in \right \rangle }$
from the parameter
![]() $\varnothing $
, and we could dispense with the predicate
$\varnothing $
, and we could dispense with the predicate
![]() ${\mathbb A}$
by instead specifying
${\mathbb A}$
by instead specifying
![]() $\varnothing $
as a constant.
$\varnothing $
as a constant.
1.1 Axioms
In the urelement context, the axiom of extensionality should be taken as the assertion that whenever two sets—two non-urelement objects—have all the same elements, then they are identical. The urelements, of course, have all the same elements as each other, none, but they are not sets and so do not constitute a counterexample to this formulation of extensionality. The other axioms we include in the theory ZFCU of set theory with urelements are the axioms of foundation, pairing, union, power set, infinity, the separation scheme, the collection scheme, and the axiom of choice, all stated in the language of urelement set theory
![]() $\{{\in ,{\mathbb A}}\}$
. Without the axiom of choice, we denote the theory by ZFU.
$\{{\in ,{\mathbb A}}\}$
. Without the axiom of choice, we denote the theory by ZFU.
Note that we include collection as an axiom of ZFCU, but be careful, since not all authors do so. The replacement axiom, of course, is a consequence of collection and separation, but the converse is not true, and we shall prove (page 4) that it is a strictly weaker theory to omit the collection axiom. The reader should take note in urelement set theory that many familiar set-theoretic arguments and results, which work as expected in ZF or ZFC set theory, break down in the urelement context unless one has adopted just the right principles to support them. One example is the failure we just mentioned of the implication from replacement to collection over the other axioms. Another easy example might be the fact that the rank hierarchy
![]() $V_{\alpha }(A)$
, defined below, is not set-like when there are a proper class of urelements—the levels of the cumulative hierarchy are each a proper class, if A is. A third example is that, while in ZFC one can prove the first-order
$V_{\alpha }(A)$
, defined below, is not set-like when there are a proper class of urelements—the levels of the cumulative hierarchy are each a proper class, if A is. A third example is that, while in ZFC one can prove the first-order
![]() $\alpha $
-dependent choice scheme
$\alpha $
-dependent choice scheme
![]() $\alpha $
-DC for every ordinal
$\alpha $
-DC for every ordinal
![]() $\alpha $
, that is, for definable class relations, this is not true in ZFCU, even though this theory has the axiom of choice, collection, replacement, reflection, and other principles that might be deemed relevant (see page 5). The general lesson is that in urelement set theory, one should ensure that one has the right theory for whatever argument is at hand.
$\alpha $
, that is, for definable class relations, this is not true in ZFCU, even though this theory has the axiom of choice, collection, replacement, reflection, and other principles that might be deemed relevant (see page 5). The general lesson is that in urelement set theory, one should ensure that one has the right theory for whatever argument is at hand.
In the language of pure set theory
![]() $\in $
, there is a sense in which one can regard ZFCU as a subtheory of ZFC, since ultimately we have simply weakened the extensionality axiom to accommodate urelements (making sure also to retain the collection axiom). But in this language, one cannot distinguish
$\in $
, there is a sense in which one can regard ZFCU as a subtheory of ZFC, since ultimately we have simply weakened the extensionality axiom to accommodate urelements (making sure also to retain the collection axiom). But in this language, one cannot distinguish
![]() $\varnothing $
from the urelements, and so one needs
$\varnothing $
from the urelements, and so one needs
![]() $\varnothing $
as a parameter or constant in this formulation of the theory, if one intends to distinguish it from the atoms.
$\varnothing $
as a parameter or constant in this formulation of the theory, if one intends to distinguish it from the atoms.
1.2 The urelement support of a set
For any set u consider the urelements of which it is formed, the atoms appearing in the transitive closure
![]() $\mathop {\mathrm {TC}}(u)$
of the set, the smallest transitive set containing u. The urelement support of a set u, also known as the kernel of u, is the set of urelements appearing in the transitive closure of u. For any set or class of urelements
$\mathop {\mathrm {TC}}(u)$
of the set, the smallest transitive set containing u. The urelement support of a set u, also known as the kernel of u, is the set of urelements appearing in the transitive closure of u. For any set or class of urelements
![]() $B\subseteq A$
, we may form the class
$B\subseteq A$
, we may form the class
![]() $V(B)$
consisting of all sets u whose support is contained in B. The class of pure sets V is therefore the same as
$V(B)$
consisting of all sets u whose support is contained in B. The class of pure sets V is therefore the same as
![]() $V(\varnothing )$
, the sets with no urelements in their transitive closure. Since every set u is supported by some set of urelements, it follows that
$V(\varnothing )$
, the sets with no urelements in their transitive closure. Since every set u is supported by some set of urelements, it follows that
![]() $V(A)=\bigcup _{w\subseteq A}V(w)$
, where w ranges over all possible sets of urelements.
$V(A)=\bigcup _{w\subseteq A}V(w)$
, where w ranges over all possible sets of urelements.
For any class of urelements
![]() $B\subseteq A$
, the model
$B\subseteq A$
, the model
![]() $V(B)$
is a transitive class containing all pure sets and closed under pairing, union, and power set. This is therefore a model of the axioms of extensionality, foundation, pairing, union, power set, infinity, and separation, as well as the axiom of choice, provided these hold in
$V(B)$
is a transitive class containing all pure sets and closed under pairing, union, and power set. This is therefore a model of the axioms of extensionality, foundation, pairing, union, power set, infinity, and separation, as well as the axiom of choice, provided these hold in
![]() $V(A)$
. If the collection axiom holds in
$V(A)$
. If the collection axiom holds in
![]() $V(A)$
, then it will also hold in
$V(A)$
, then it will also hold in
![]() $V(B)$
, since if
$V(B)$
, since if
![]() $u\in V(B)$
and every
$u\in V(B)$
and every
![]() $x\in u$
has a witness
$x\in u$
has a witness
![]() $y\in V(B)$
that
$y\in V(B)$
that
![]() $\varphi (x,y)^{V(B)}$
, then we may collect these in
$\varphi (x,y)^{V(B)}$
, then we may collect these in
![]() $V(A)$
, and the collecting set can be restricted to its instances in
$V(A)$
, and the collecting set can be restricted to its instances in
![]() $V(B)$
, which has support in B—more generally,
$V(B)$
, which has support in B—more generally,
![]() $V(B)$
contains every subset of it that exists in
$V(B)$
contains every subset of it that exists in
![]() $V(A)$
. In short,
$V(A)$
. In short,
![]() $V(B)$
will be a model of ZFCU whenever
$V(B)$
will be a model of ZFCU whenever
![]() $V(A)$
is.
$V(A)$
is.
1.3 The rank hierarchy
In ZFC set theory, the universe V of pure sets is stratified into the familiar cumulative
![]() $V_{\alpha }$
hierarchy of rank, which can be defined by iterating the power set operator, starting with
$V_{\alpha }$
hierarchy of rank, which can be defined by iterating the power set operator, starting with
![]() $V_0=\varnothing $
, taking power set at successors
$V_0=\varnothing $
, taking power set at successors
![]() $V_{\alpha +1}=P(V_{\alpha })$
, and unions at limits
$V_{\alpha +1}=P(V_{\alpha })$
, and unions at limits
![]() $V_{\lambda }=\bigcup _{\alpha <\lambda }V_{\alpha }$
. Alternatively, one can define the rank of a set directly, with the recursive definition
$V_{\lambda }=\bigcup _{\alpha <\lambda }V_{\alpha }$
. Alternatively, one can define the rank of a set directly, with the recursive definition
![]() $\rho (y)=\sup \{{\rho (x)+1\mid x\in y}\}$
. The rank
$\rho (y)=\sup \{{\rho (x)+1\mid x\in y}\}$
. The rank
![]() $\rho (y)$
is the smallest ordinal for which
$\rho (y)$
is the smallest ordinal for which
![]() $y\in V_{\rho (y)+1}$
, and so
$y\in V_{\rho (y)+1}$
, and so
![]() $V_{\alpha }$
is the collection of sets having rank less than
$V_{\alpha }$
is the collection of sets having rank less than
![]() $\alpha $
.
$\alpha $
.
In the urelement context
![]() $V(A)$
, one can attempt to iterate the power set by defining
$V(A)$
, one can attempt to iterate the power set by defining
![]() $V_0(A)=A$
, taking the power set (power class) with
$V_0(A)=A$
, taking the power set (power class) with
![]() $V_{\alpha +1}(A)=P(V_{\alpha }(A))$
and unions at limits
$V_{\alpha +1}(A)=P(V_{\alpha }(A))$
and unions at limits
![]() $V_{\lambda }(A)=\bigcup _{\alpha <\lambda }V_{\alpha }(A)$
. When A is a set, this works completely fine. When A is a proper class, however, this recursion is not set-like, because every
$V_{\lambda }(A)=\bigcup _{\alpha <\lambda }V_{\alpha }(A)$
. When A is a set, this works completely fine. When A is a proper class, however, this recursion is not set-like, because every
![]() $V_{\alpha }(A)$
will be a proper class. Furthermore, in the proper class case this manner of definition is problematic, because one cannot generally undertake class recursions of this form without additional axiomatic power—the principle of elementary transfinite recursion ETR, asserting that all first-order class recursions along class well-ordered relations have solutions, is known to have consistency strength strictly stronger than GBC, even for class recursions of length
$V_{\alpha }(A)$
will be a proper class. Furthermore, in the proper class case this manner of definition is problematic, because one cannot generally undertake class recursions of this form without additional axiomatic power—the principle of elementary transfinite recursion ETR, asserting that all first-order class recursions along class well-ordered relations have solutions, is known to have consistency strength strictly stronger than GBC, even for class recursions of length
![]() $\omega $
(see [Reference Gitman, Hamkins, Caicedo, Cummings, Koellner and Larson6]).
$\omega $
(see [Reference Gitman, Hamkins, Caicedo, Cummings, Koellner and Larson6]).
Nevertheless, the rank recursion can be successfully undertaken in urelement set theory by defining the rank function directly on individual sets with the recursion
![]() $\rho (y)=\sup \{{\rho (x)+1\mid x\in y}\}$
, adding that
$\rho (y)=\sup \{{\rho (x)+1\mid x\in y}\}$
, adding that
![]() for the atoms. Thus, we can define the class
for the atoms. Thus, we can define the class
![]() $V_{\alpha }(A)$
to be the atoms and sets with rank less than
$V_{\alpha }(A)$
to be the atoms and sets with rank less than
![]() $\alpha $
. In this way, we achieve a rank hierarchy on
$\alpha $
. In this way, we achieve a rank hierarchy on
![]() $V(A)$
.
$V(A)$
.
An alternative way to realize this is to define
![]() $V_{\alpha }(A)$
to be the union of
$V_{\alpha }(A)$
to be the union of
![]() $V_{\alpha }(w)$
for any set of atoms
$V_{\alpha }(w)$
for any set of atoms
![]() $w\subseteq A$
, using the fact that the powerset-iteration construction works fine for
$w\subseteq A$
, using the fact that the powerset-iteration construction works fine for
![]() $V_{\alpha }(w)$
, stratifying the class
$V_{\alpha }(w)$
, stratifying the class
![]() $V(w)$
, and every set in
$V(w)$
, and every set in
![]() $V(A)$
is in some
$V(A)$
is in some
![]() $V(w)$
, where w is the set of atoms supporting the given set.
$V(w)$
, where w is the set of atoms supporting the given set.
 $$ \begin{align*}V(A)=\bigcup_{\genfrac{}{}{0pt}{2}{\alpha\in\mathord{\mathrm{Ord}}}{w\subseteq A}}V_{\alpha}(w).\end{align*} $$
$$ \begin{align*}V(A)=\bigcup_{\genfrac{}{}{0pt}{2}{\alpha\in\mathord{\mathrm{Ord}}}{w\subseteq A}}V_{\alpha}(w).\end{align*} $$
Thus, the universe
![]() $V(A)$
is realized as a two-dimensional set-like cumulative hierarchy, a potentialist system that allows both for increasing height as
$V(A)$
is realized as a two-dimensional set-like cumulative hierarchy, a potentialist system that allows both for increasing height as
![]() $\alpha $
increases and increasing width as one increases the set of urelements
$\alpha $
increases and increasing width as one increases the set of urelements
![]() $w\subseteq A$
used for support.
$w\subseteq A$
used for support.
1.4 Rigidity and nonrigidity
In ZFC set theory, every transitive set and class is rigid and two transitive sets are isomorphic with respect to
![]() $\in $
if and only if they are identical. This is because if X and Y are transitive classes of pure sets and
$\in $
if and only if they are identical. This is because if X and Y are transitive classes of pure sets and
![]() $\pi :{\left \langle X,\in \right \rangle } \to {\left \langle Y,\in \right \rangle }$
is an
$\pi :{\left \langle X,\in \right \rangle } \to {\left \langle Y,\in \right \rangle }$
is an
![]() $\in $
-isomorphism, then necessarily
$\in $
-isomorphism, then necessarily
![]() $\pi (y)=\{{\pi (x)\mid x\in y}\}$
, and so by
$\pi (y)=\{{\pi (x)\mid x\in y}\}$
, and so by
![]() $\in $
-induction it follows that
$\in $
-induction it follows that
![]() $\pi (y)=y$
and consequently
$\pi (y)=y$
and consequently
![]() $X=Y$
and
$X=Y$
and
![]() $\pi =\mathop {\mathrm {\small id}}$
. In particular, every transitive set in ZFC is rigid with respect to
$\pi =\mathop {\mathrm {\small id}}$
. In particular, every transitive set in ZFC is rigid with respect to
![]() $\in $
, and the set-theoretic universe
$\in $
, and the set-theoretic universe
![]() ${\left \langle V,\in \right \rangle }$
can have no definable automorphisms (allowing parameters).
${\left \langle V,\in \right \rangle }$
can have no definable automorphisms (allowing parameters).
With urelements, however, this rigidity phenomenon breaks down dramatically, and any two equinumerous classes of atoms B and C give rise to isomorphic corresponding transitive universes
![]() ${\left \langle V(B),\in \right \rangle }$
and
${\left \langle V(B),\in \right \rangle }$
and
![]() ${\left \langle V(C),\in \right \rangle }$
. Specifically, any bijection
${\left \langle V(C),\in \right \rangle }$
. Specifically, any bijection
![]() $\pi :B\to C$
can be recursively extended by defining
$\pi :B\to C$
can be recursively extended by defining
![]() $\pi (y)=\{{\pi (x)\mid x\in y}\}$
, which will ensure the isomorphism property
$\pi (y)=\{{\pi (x)\mid x\in y}\}$
, which will ensure the isomorphism property
![]() $x\in y\mathrel {\leftrightarrow }\pi (x)\in \pi (y)$
. Similarly, any permutation
$x\in y\mathrel {\leftrightarrow }\pi (x)\in \pi (y)$
. Similarly, any permutation
![]() $\pi :A\to A$
extends to an automorphism of the full set-theoretic universe
$\pi :A\to A$
extends to an automorphism of the full set-theoretic universe
![]() $V(A)$
itself. When there are at least two urelements atoms, therefore, the universe
$V(A)$
itself. When there are at least two urelements atoms, therefore, the universe
![]() $V(A)$
is not rigid. Precisely because the atoms are taken to be irreducible mathematical objects with no internal set-theoretic structure, they are set-theoretically indistinguishable, and so it becomes a fundamental part of the urelement perspective that the set-theoretic universe is homogeneous with respect to the urelement atoms. Meanwhile, perhaps one introduces urelements, such as numbers or geometric points, with an intended structure to be built on top of them; the homogeneity automorphisms would carry that structure to an alternative isomorphic copy.
$V(A)$
is not rigid. Precisely because the atoms are taken to be irreducible mathematical objects with no internal set-theoretic structure, they are set-theoretically indistinguishable, and so it becomes a fundamental part of the urelement perspective that the set-theoretic universe is homogeneous with respect to the urelement atoms. Meanwhile, perhaps one introduces urelements, such as numbers or geometric points, with an intended structure to be built on top of them; the homogeneity automorphisms would carry that structure to an alternative isomorphic copy.
1.5 Consequences of nonrigidity for urelement set theory
This abundance of automorphisms has various effects on the set-theoretic foundations, causing sets to work differently than might naively be expected.
One such effect, as we mentioned earlier, is that the axiom of collection does not follow from the axiom of replacement, as it does in ordinary ZFC set theory. To see this, assume
![]() $V(A)$
has infinitely many urelements and let W be the class of finitely supported sets, that is, the class of sets u whose transitive closure has only finitely many atoms. Equivalently,
$V(A)$
has infinitely many urelements and let W be the class of finitely supported sets, that is, the class of sets u whose transitive closure has only finitely many atoms. Equivalently,
![]() $W=\bigcup _{\text {finite }w\subseteq A}V(w)$
, where w ranges over the finite sets of atoms. We observe easily that W is a supertransitive class (a transitive class containing all subsets of its members), and closed under pairing, union, and power set, and so W is easily seen to satisfy extensionality, foundation, pairing, union, power set, separation, as well as the axiom of choice, assuming these hold in
$W=\bigcup _{\text {finite }w\subseteq A}V(w)$
, where w ranges over the finite sets of atoms. We observe easily that W is a supertransitive class (a transitive class containing all subsets of its members), and closed under pairing, union, and power set, and so W is easily seen to satisfy extensionality, foundation, pairing, union, power set, separation, as well as the axiom of choice, assuming these hold in
![]() $V(A)$
.
$V(A)$
.
The class W also satisfies replacement, as observed by Lévy [Reference Lévy, Bulloff, Holyoke and Hahn15]. To see this, suppose that u has finite support
![]() $w=\{{a_0,\ldots ,a_n}\}$
and every
$w=\{{a_0,\ldots ,a_n}\}$
and every
![]() $x\in u$
has some unique
$x\in u$
has some unique
![]() $y\in W$
for which W satisfies
$y\in W$
for which W satisfies
![]() $\varphi (x,y)$
. Note that every
$\varphi (x,y)$
. Note that every
![]() $x\in u$
is also in
$x\in u$
is also in
![]() $V(w)$
. What we claim is that every
$V(w)$
. What we claim is that every
![]() $x\in u$
has the corresponding y also in
$x\in u$
has the corresponding y also in
![]() $V(w)$
, for if y has some other atoms in its transitive closure, not amongst
$V(w)$
, for if y has some other atoms in its transitive closure, not amongst
![]() $a_0,\ldots ,a_n$
, then we could apply an automorphism
$a_0,\ldots ,a_n$
, then we could apply an automorphism
![]() $\pi $
to A that fixes each
$\pi $
to A that fixes each
![]() $a_0,\ldots ,a_n$
but moves these other atoms to further distinct atoms not appearing in the transitive closure of y, causing
$a_0,\ldots ,a_n$
but moves these other atoms to further distinct atoms not appearing in the transitive closure of y, causing
![]() $\pi (y)\neq y$
. But since
$\pi (y)\neq y$
. But since
![]() $\pi $
would be an automorphism of W fixing u, this other set
$\pi $
would be an automorphism of W fixing u, this other set
![]() $\pi (y)$
would also fulfill the condition
$\pi (y)$
would also fulfill the condition
![]() $\varphi (x,\pi (y))$
in W, contrary to uniqueness. So every witness y must be in
$\varphi (x,\pi (y))$
in W, contrary to uniqueness. So every witness y must be in
![]() $V(a_0,\ldots ,a_n)$
. Therefore the image set of all such witnesses
$V(a_0,\ldots ,a_n)$
. Therefore the image set of all such witnesses
![]() $\{{y\mid \exists x\in u\,\varphi ^W(x,y)}\}$
, which is a set by the replacement axiom in
$\{{y\mid \exists x\in u\,\varphi ^W(x,y)}\}$
, which is a set by the replacement axiom in
![]() $V(A)$
, would exist in
$V(A)$
, would exist in
![]() $V(a_0,\ldots ,a_n)$
, fulfilling the replacement axiom of W.
$V(a_0,\ldots ,a_n)$
, fulfilling the replacement axiom of W.
Meanwhile, the bad news is that the class of finitely supported sets W does not fulfill the axiom of collection. Namely, for every natural number n, there is a set consisting of n urelements, but there is no set having such witness sets for every
![]() $n\in \omega $
, since every set in W has only finite support amongst the atoms; this is a violation of the collection axiom.
$n\in \omega $
, since every set in W has only finite support amongst the atoms; this is a violation of the collection axiom.
The situation at bottom is extremely similar to the analogous failures of collection described in [Reference Gitman, Hamkins and Johnstone8] for the naive axiomatizations of set theory without power set, which use merely the replacement axiom rather than collection plus separation. The main fact, first observed by Zarach [Reference Zarach and Hájek27] and extended by Freire and Hamkins [Reference Gitman, Hamkins and Johnstone8], is that all kinds of things go wrong when one uses the naive theory for ZFC without power set—the collection axiom can fail; the cardinal
![]() $\omega _1$
can be singular, even when the axiom of choice holds; there can be sets of reals of every size
$\omega _1$
can be singular, even when the axiom of choice holds; there can be sets of reals of every size
![]() $\aleph _n$
, but no set of reals of size
$\aleph _n$
, but no set of reals of size
![]() $\aleph _{\omega }$
; the Łoś theorem can fail badly, even when choice holds; the Łoś theorem can fail even in the case of a measurable cardinal
$\aleph _{\omega }$
; the Łoś theorem can fail badly, even when choice holds; the Łoś theorem can fail even in the case of a measurable cardinal
![]() $\kappa $
; the class of
$\kappa $
; the class of
![]() $\Sigma _1$
definable sets can fail to be closed under bounded quantifiers. Meanwhile, the research literature unfortunately has numerous instances (identified in [Reference Gitman, Hamkins and Johnstone8]) where researchers provide the naive axiomatization of
$\Sigma _1$
definable sets can fail to be closed under bounded quantifiers. Meanwhile, the research literature unfortunately has numerous instances (identified in [Reference Gitman, Hamkins and Johnstone8]) where researchers provide the naive axiomatization of
![]() $\mathrm {ZFC}^-$
, but then presume that the various problematic features do not occur, even though this is not provable in their theory. In light of these failures, the main conclusion to be drawn is that the naive axiomatization is simply a mistake—the correct axiomatization of ZFC without power set uses collection and separation, rather than mere replacement. This is the theory that holds in the natural instances and applications of this theory, such as the use in
$\mathrm {ZFC}^-$
, but then presume that the various problematic features do not occur, even though this is not provable in their theory. In light of these failures, the main conclusion to be drawn is that the naive axiomatization is simply a mistake—the correct axiomatization of ZFC without power set uses collection and separation, rather than mere replacement. This is the theory that holds in the natural instances and applications of this theory, such as the use in
![]() $H_{\kappa ^+}$
, and to our knowledge all of the erroneous uses and applications of the theory are easily and completely corrected simply by using this stronger version of the theory.
$H_{\kappa ^+}$
, and to our knowledge all of the erroneous uses and applications of the theory are easily and completely corrected simply by using this stronger version of the theory.
The situation in urelement set theory is analogous. One should include the collection and separation axioms in ZFCU, not just replacement, or else face a similar phenomenon of unexpected, undesirable effects.
Unfortunately, the collection/replacement issue is not the end of the story, for there are further unwelcome situations that are possible even when one does include the collection axiom.Footnote
1
To see this, assume we have uncountably many atoms and consider the class
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
of all (atoms and) countably supported sets. That is, let
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
of all (atoms and) countably supported sets. That is, let
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}=\bigcup _{\text {countable }w\subseteq A}V(w)$
. This class
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}=\bigcup _{\text {countable }w\subseteq A}V(w)$
. This class
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
will satisfy extensionality, foundation, pairing, union, power set, separation, choice, infinity, and replacement. Furthermore, this class
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
will satisfy extensionality, foundation, pairing, union, power set, separation, choice, infinity, and replacement. Furthermore, this class
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
satisfies the collection axiom. To see this, suppose that
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
satisfies the collection axiom. To see this, suppose that
![]() $u\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
and for every
$u\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
and for every
![]() $x\in u$
there is
$x\in u$
there is
![]() $y\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
for which
$y\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
for which
![]() $\varphi (x,y)$
holds in
$\varphi (x,y)$
holds in
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
. Let w be the support of u in the atoms, and extend this set of atoms
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
. Let w be the support of u in the atoms, and extend this set of atoms
![]() $w\subseteq \bar w$
by adding countably many additional atoms. Since every individual
$w\subseteq \bar w$
by adding countably many additional atoms. Since every individual
![]() $y\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
has countable support in the atoms, there is an automorphism
$y\in {\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
has countable support in the atoms, there is an automorphism
![]() $\pi :V(A)\to V(A)$
fixing every
$\pi :V(A)\to V(A)$
fixing every
![]() $a\in w$
and for which
$a\in w$
and for which
![]() $\pi (y)\in V(\bar w)$
. That is, whichever new atoms y used outside w, we can map them into
$\pi (y)\in V(\bar w)$
. That is, whichever new atoms y used outside w, we can map them into
![]() $\bar w$
and thereby place
$\bar w$
and thereby place
![]() $\pi (y)$
in
$\pi (y)$
in
![]() $V(\bar w)$
. Thus, the witnesses y can always be found inside
$V(\bar w)$
. Thus, the witnesses y can always be found inside
![]() $V(\bar w)$
, and consequently we can realize the collection axiom inside some sufficiently large
$V(\bar w)$
, and consequently we can realize the collection axiom inside some sufficiently large
![]() $V_{\alpha }(\bar w)$
.
$V_{\alpha }(\bar w)$
.
Meanwhile, the model
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
has a strange property: the class of all urelements A is a proper class, but every set of atoms is countable. It follows that ZFCU does not prove that any set can be mapped injectively to any proper class. Moreover, although every countable sequence of distinct atoms can be extended further, and every chain of such sequences has its union as an upper bound, and
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
has a strange property: the class of all urelements A is a proper class, but every set of atoms is countable. It follows that ZFCU does not prove that any set can be mapped injectively to any proper class. Moreover, although every countable sequence of distinct atoms can be extended further, and every chain of such sequences has its union as an upper bound, and
![]() $\omega _1$
exists, yet there is no
$\omega _1$
exists, yet there is no
![]() $\omega _1$
-sequence of distinct atoms in
$\omega _1$
-sequence of distinct atoms in
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
. This is a violation of the
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
. This is a violation of the
![]() $\omega _1$
-dependent choice scheme
$\omega _1$
-dependent choice scheme
![]() $\omega _1$
-DC, asserting that if
$\omega _1$
-DC, asserting that if
![]() $T\subseteq V(A)^{<\omega _1}$
is a definable class tree of countable sequences, such that every sequence in T has a proper extension in T and every countable chain in T has an upper bound in T, then T admits a branch of length
$T\subseteq V(A)^{<\omega _1}$
is a definable class tree of countable sequences, such that every sequence in T has a proper extension in T and every countable chain in T has an upper bound in T, then T admits a branch of length
![]() $\omega _1$
.
$\omega _1$
.
This situation is counterintuitive because the
![]() $\omega _1$
-dependent choice scheme is provable in ZFC set theory—perhaps we usually think of it as an elementary consequence of the axiom of choice and collection in the ZFC context. And yet, it is not provable in ZFCU, even though this theory has the axiom of choice, collection, replacement, and (we shall show) the reflection principle. One can similarly make models where the failure of
$\omega _1$
-dependent choice scheme is provable in ZFC set theory—perhaps we usually think of it as an elementary consequence of the axiom of choice and collection in the ZFC context. And yet, it is not provable in ZFCU, even though this theory has the axiom of choice, collection, replacement, and (we shall show) the reflection principle. One can similarly make models where the failure of
![]() $\alpha $
-DC occurs first at higher ordinals
$\alpha $
-DC occurs first at higher ordinals
![]() $\alpha $
.
$\alpha $
.
Let us exhibit another instance of strange behavior in urelement set theory. Suppose that we have a model of ZFCU with the urelements forming a set of size
![]() $\omega _1$
. Let us split the
$\omega _1$
. Let us split the
![]() $\omega _1$
many urelements into two disjoint sets
$\omega _1$
many urelements into two disjoint sets
![]() $A\sqcup B$
, both of size
$A\sqcup B$
, both of size
![]() $\omega _1$
. Now define Y as the class of sets u in
$\omega _1$
. Now define Y as the class of sets u in
![]() $V(A\cup B)$
whose support has at most countable intersection with B. So every set of urelements in Y is contained in
$V(A\cup B)$
whose support has at most countable intersection with B. So every set of urelements in Y is contained in
![]() $A\cup w$
for some countable subset
$A\cup w$
for some countable subset
![]() $w\subseteq B$
. Meanwhile, we can prove that Y is a model of ZFCU just as with
$w\subseteq B$
. Meanwhile, we can prove that Y is a model of ZFCU just as with
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
above. The curious thing to notice about this model Y is that the urelements do not form a set—they are a proper class—and A is a set of urelements in Y of size
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
above. The curious thing to notice about this model Y is that the urelements do not form a set—they are a proper class—and A is a set of urelements in Y of size
![]() $\omega _1$
, but all sets of urelements disjoint from A are countable. So we cannot find a duplicate of A in the urelements disjoint from A.
$\omega _1$
, but all sets of urelements disjoint from A are countable. So we cannot find a duplicate of A in the urelements disjoint from A.
One way to reintroduce a measure of rigidity into urelement set theory is to provide a fixed enumeration of the atoms by a class of pure sets. Or simply to well-order the atoms. Consider for example the structure
![]() ${\left \langle V(A),\in ,<\right \rangle }$
, where
${\left \langle V(A),\in ,<\right \rangle }$
, where
![]() $<$
is a well-ordering of the atoms, not necessarily set-like. This universe is definably rigid, because if
$<$
is a well-ordering of the atoms, not necessarily set-like. This universe is definably rigid, because if
![]() $\pi :V(A)\to V(A)$
is a definable automorphism, then in respecting
$\pi :V(A)\to V(A)$
is a definable automorphism, then in respecting
![]() $<$
it must consequently fix every atom, since there can be no least element moved, and since also
$<$
it must consequently fix every atom, since there can be no least element moved, and since also
![]() $\pi (y)=\{{\pi (x)\mid x\in y}\}$
for the sets, it follows by
$\pi (y)=\{{\pi (x)\mid x\in y}\}$
for the sets, it follows by
![]() $\in $
-induction that
$\in $
-induction that
![]() $\pi (y)=y$
and so
$\pi (y)=y$
and so
![]() $\pi $
is the identity. In this expanded signature, the class W of (atoms and) finitely supported sets no longer satisfies replacement, when there are infinitely many atoms, since for each n there is a unique atom
$\pi $
is the identity. In this expanded signature, the class W of (atoms and) finitely supported sets no longer satisfies replacement, when there are infinitely many atoms, since for each n there is a unique atom
![]() $a_n$
that is nth in the order
$a_n$
that is nth in the order
![]() $<$
, but the set of all these atoms is not finitely supported. Similarly, the class
$<$
, but the set of all these atoms is not finitely supported. Similarly, the class
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
of (atoms and) countably supported sets does not satisfy replacement in the expanded language, when there are uncountably many atoms, because for each countable ordinal
${\mkern 3.5mu\overline {\mkern -3.5mu W\mkern -.5mu}\mkern .5mu}$
of (atoms and) countably supported sets does not satisfy replacement in the expanded language, when there are uncountably many atoms, because for each countable ordinal
![]() $\alpha $
there is an
$\alpha $
there is an
![]() $\alpha $
th atom, but the set of these is not countably supported.
$\alpha $
th atom, but the set of these is not countably supported.
An alternative method, which we shall employ in the next section, is to introduce a predicate
![]() $\smash {\vec {{\mathbb A}}}$
for explicitly enumerating the urelements by a class of pure sets. The predicate
$\smash {\vec {{\mathbb A}}}$
for explicitly enumerating the urelements by a class of pure sets. The predicate
![]() $\smash {\vec {{\mathbb A}}}(i,a_i)$
will associate each element
$\smash {\vec {{\mathbb A}}}(i,a_i)$
will associate each element
![]() $i\in I$
in some class I of pure sets with a distinct urelement
$i\in I$
in some class I of pure sets with a distinct urelement
![]() $a_i$
. For example, perhaps we shall have exactly
$a_i$
. For example, perhaps we shall have exactly
![]() $\omega $
many urelements, or
$\omega $
many urelements, or
![]() ${\mathbb R}$
many, or
${\mathbb R}$
many, or
![]() $\mathord {\mathrm {Ord}}$
many, or V many urelements.
$\mathord {\mathrm {Ord}}$
many, or V many urelements.
2 Interpreting urelement set theory in ZFC
Let us describe next how to interpret urelement set theory inside the urelement-free set theories ZF and ZFC. The fact that this is possible, and furthermore the fact that it is possible in a way that achieves strong axioms for the interpreted urelement set theories, such as “there are a proper class of atoms” or even “the atoms can be well-ordered in type
![]() $\mathord {\mathrm {Ord}}$
,” tends to support the view that the foundational roles sought for the urelement theories can also be undertaken ultimately without urelements by interpreting these urelement theories inside ZFC. On this view, one will not identify any new mathematical structure or relation in these urelement set theories that we cannot in principle find already in ZFC.
$\mathord {\mathrm {Ord}}$
,” tends to support the view that the foundational roles sought for the urelement theories can also be undertaken ultimately without urelements by interpreting these urelement theories inside ZFC. On this view, one will not identify any new mathematical structure or relation in these urelement set theories that we cannot in principle find already in ZFC.
Assume V is a set-theoretic universe satisfying ZFC, and suppose A is any class of sets in V. (In the ZFC context, we assume A is a definable class, but we shall later move to the GBC context, where we drop the definability requirement.) Inside V we shall presently define a certain model of urelement set theory
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, a model of
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, a model of
![]() $\mathrm {ZFCU}$
in which the urelements will be indexed by the class A, whose pure sets, furthermore, will be an exact copy of V.
$\mathrm {ZFCU}$
in which the urelements will be indexed by the class A, whose pure sets, furthermore, will be an exact copy of V.
We begin by making a copy of A with
![]() $\bar A=\{{0}\}\times A$
, representing every object
$\bar A=\{{0}\}\times A$
, representing every object
![]() $a\in A$
by its copy
$a\in A$
by its copy
![]() $\bar a={\left \langle 0,a\right \rangle }$
. These will be the urelements of
$\bar a={\left \langle 0,a\right \rangle }$
. These will be the urelements of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, and we accordingly place
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, and we accordingly place
![]() $\bar A\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Next, we simply close
$\bar A\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Next, we simply close
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
under the operation: if
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
under the operation: if
![]() $y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, then
$y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, then
![]() $\bar y={\left \langle 1,y\right \rangle }\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. That is,
$\bar y={\left \langle 1,y\right \rangle }\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. That is,
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is the smallest class of sets containing
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is the smallest class of sets containing
![]() $\bar A$
and closed under that operation. One may undertake this as a set-like transfinite recursion in ZF by forming a hierarchy
$\bar A$
and closed under that operation. One may undertake this as a set-like transfinite recursion in ZF by forming a hierarchy
![]() $V_{\alpha }{\mathopen {\lbrack \!\lbrack }A\cap V_{\alpha }\mathclose {\rbrack \!\rbrack }}$
, gradually adding atoms and closing under the operation as the recursion progresses. The central idea is that
$V_{\alpha }{\mathopen {\lbrack \!\lbrack }A\cap V_{\alpha }\mathclose {\rbrack \!\rbrack }}$
, gradually adding atoms and closing under the operation as the recursion progresses. The central idea is that
![]() $\bar y={\left \langle 1,y\right \rangle }$
will be the set in
$\bar y={\left \langle 1,y\right \rangle }$
will be the set in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
whose elements are the (actual) elements of y. Thus, we define the membership relation as
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
whose elements are the (actual) elements of y. Thus, we define the membership relation as
![]() $x\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu} \bar y$
if and only if
$x\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu} \bar y$
if and only if
![]() $x\in y$
, where
$x\in y$
, where
![]() $\bar y={\left \langle 1,y\right \rangle }$
. The relation
$\bar y={\left \langle 1,y\right \rangle }$
. The relation
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
is therefore set-like and well-founded in V, because
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
is therefore set-like and well-founded in V, because
![]() $x\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu} \bar y$
requires that x has lower rank than
$x\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu} \bar y$
requires that x has lower rank than
![]() $\bar y$
. In short, the definition is that every object in
$\bar y$
. In short, the definition is that every object in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will be an ordered pair, with the urelements having the form
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will be an ordered pair, with the urelements having the form
![]() $\bar a={\left \langle 0,a\right \rangle }$
for
$\bar a={\left \langle 0,a\right \rangle }$
for
![]() $a\in A$
and fulfilling
$a\in A$
and fulfilling
![]() ${\mathbb A}(\bar a)$
and the sets having the form
${\mathbb A}(\bar a)$
and the sets having the form
![]() $\bar y={\left \langle 1,y\right \rangle }$
for some
$\bar y={\left \langle 1,y\right \rangle }$
for some
![]() $y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, with the
$y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, with the
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements of
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements of
![]() $\bar y$
being simply the actual members of y.
$\bar y$
being simply the actual members of y.
The claim is that
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
is a model of ZFCU. Extensionality holds because the urelements have no
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
is a model of ZFCU. Extensionality holds because the urelements have no
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-members and if
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-members and if
![]() $\bar y={\left \langle 1,y\right \rangle }$
and
$\bar y={\left \langle 1,y\right \rangle }$
and
![]() $\bar z={\left \langle 1,z\right \rangle }$
have the same
$\bar z={\left \langle 1,z\right \rangle }$
have the same
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements, then necessarily
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements, then necessarily
![]() $y=z$
and consequently
$y=z$
and consequently
![]() $\bar y=\bar z$
. Foundation holds because
$\bar y=\bar z$
. Foundation holds because
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
is well-founded—the
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
is well-founded—the
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements of a set have lower rank in V. It is easy to show that
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
-elements of a set have lower rank in V. It is easy to show that
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
has the union, pairing, and power set axioms simply by constructing the appropriate representing set in each case. For example, if
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
has the union, pairing, and power set axioms simply by constructing the appropriate representing set in each case. For example, if
![]() $u,v\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, then
$u,v\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, then
![]() ${\left \langle 1,\{{u,v}\}\right \rangle }$
will represent the unordered pair
${\left \langle 1,\{{u,v}\}\right \rangle }$
will represent the unordered pair
![]() $\{{u,v}\}$
in
$\{{u,v}\}$
in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. We get the separation, replacement, and collection axioms because every subset
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. We get the separation, replacement, and collection axioms because every subset
![]() $y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
that is realized in V is represented by the set
$y\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
that is realized in V is represented by the set
![]() $\bar y\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Similarly, the axiom of choice holds in
$\bar y\in V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Similarly, the axiom of choice holds in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, if it holds in V, because we can form a suitable set y of choices in V, and then consider the corresponding set
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, if it holds in V, because we can form a suitable set y of choices in V, and then consider the corresponding set
![]() $\bar y$
in
$\bar y$
in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
Every set u in V will be represented by a corresponding set
![]() $\check u={\left \langle 1,\{{\check v\mid v\in u}\}\right \rangle }$
in
$\check u={\left \langle 1,\{{\check v\mid v\in u}\}\right \rangle }$
in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, for it is easy to see that
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, for it is easy to see that
![]() $v\in u\mathrel {\leftrightarrow } \check v\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\check u$
and consequently
$v\in u\mathrel {\leftrightarrow } \check v\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\check u$
and consequently
![]() ${\left \langle V,\in \right \rangle }$
is isomorphic to
${\left \langle V,\in \right \rangle }$
is isomorphic to
![]() ${\left \langle \smash {\hat V},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
, where
${\left \langle \smash {\hat V},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
, where
![]() $\hat V=\{{\check u\mid u\in V}\}$
, which is a transitive class in
$\hat V=\{{\check u\mid u\in V}\}$
, which is a transitive class in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Furthermore, using the fact that the rank of a set
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Furthermore, using the fact that the rank of a set
![]() $\bar y$
in
$\bar y$
in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is bounded by the rank of
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is bounded by the rank of
![]() $\bar y$
in V, it follows that
$\bar y$
in V, it follows that
![]() $\hat V$
consists precisely of the pure sets of
$\hat V$
consists precisely of the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. In particular, the ordinals of
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. In particular, the ordinals of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
are precisely the
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
are precisely the
![]() $\check \alpha $
for the ordinals
$\check \alpha $
for the ordinals
![]() $\alpha $
of V.
$\alpha $
of V.
Let us expand the urelement language somewhat by introducing the urelement enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
, which holds exactly in the instances
$\smash {\vec {{\mathbb A}}}$
, which holds exactly in the instances
![]() $\smash {\vec {{\mathbb A}}}(\check a,\bar a)$
when
$\smash {\vec {{\mathbb A}}}(\check a,\bar a)$
when
![]() $a\in A$
. That is,
$a\in A$
. That is,
![]() $\smash {\vec {{\mathbb A}}}$
is the graph of the function
$\smash {\vec {{\mathbb A}}}$
is the graph of the function
![]() $\check a\mapsto \bar a$
, for
$\check a\mapsto \bar a$
, for
![]() $a\in A$
. This predicate identifies the urelements—they are exactly the range of the map
$a\in A$
. This predicate identifies the urelements—they are exactly the range of the map
![]() $\smash {\vec {{\mathbb A}}}$
—and so the urelement predicate
$\smash {\vec {{\mathbb A}}}$
—and so the urelement predicate
![]() ${\mathbb A}$
is definable from
${\mathbb A}$
is definable from
![]() $\smash {\vec {{\mathbb A}}}$
. But
$\smash {\vec {{\mathbb A}}}$
. But
![]() $\smash {\vec {{\mathbb A}}}$
also provides the enumeration of the urelements by the elements of A, well, by the copy of A in the pure sets of
$\smash {\vec {{\mathbb A}}}$
also provides the enumeration of the urelements by the elements of A, well, by the copy of A in the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, that is, by the class
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, that is, by the class
![]() $\hat A=\{{\check a\mid a\in A}\}$
. This enumeration
$\hat A=\{{\check a\mid a\in A}\}$
. This enumeration
![]() $\smash {\vec {{\mathbb A}}}$
will not generally be definable from
$\smash {\vec {{\mathbb A}}}$
will not generally be definable from
![]() ${\mathbb A}$
alone, since permutations of the urelements will lead to automorphisms of
${\mathbb A}$
alone, since permutations of the urelements will lead to automorphisms of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
that preserve
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
that preserve
![]() ${\mathbb A}$
but not
${\mathbb A}$
but not
![]() $\smash {\vec {{\mathbb A}}}$
. We interpret the phrase, “there are A many atoms” as the assertion that
$\smash {\vec {{\mathbb A}}}$
. We interpret the phrase, “there are A many atoms” as the assertion that
![]() $\smash {\vec {{\mathbb A}}}$
is a bijection between A and the class of urelements. The theories
$\smash {\vec {{\mathbb A}}}$
is a bijection between A and the class of urelements. The theories
![]() $\mathrm {ZF}\vec {\mathrm {U}}$
and
$\mathrm {ZF}\vec {\mathrm {U}}$
and
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
are the analogues of
$\mathrm {ZFC}\vec {\mathrm {U}}$
are the analogues of
![]() $\mathrm {ZFU}$
and
$\mathrm {ZFU}$
and
![]() $\mathrm {ZFCU}$
in the language with the atom-enumeration predicate
$\mathrm {ZFCU}$
in the language with the atom-enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
.
$\smash {\vec {{\mathbb A}}}$
.
Theorem 2.1. For any definable class A, the ZF set-theoretic universe
![]() ${\left \langle V,\in \right \rangle }$
is bi-interpretable with the urelement set-theoretic universe
${\left \langle V,\in \right \rangle }$
is bi-interpretable with the urelement set-theoretic universe
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
, which is a model of
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
, which is a model of
![]() $\mathrm {ZF}\vec {\mathrm {U}}+$
“there are A many urelements.”
$\mathrm {ZF}\vec {\mathrm {U}}+$
“there are A many urelements.”
Proof We have already explained how
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
is defined in V, and this is half of the interpretation. For the converse interpretation, we can interpret the structure V in
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
is defined in V, and this is half of the interpretation. For the converse interpretation, we can interpret the structure V in
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
as the pure sets, since the map
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
as the pure sets, since the map
![]() $u\mapsto \check u$
is an isomorphism of
$u\mapsto \check u$
is an isomorphism of
![]() ${\left \langle V,\in \right \rangle }$
with the class of pure sets in
${\left \langle V,\in \right \rangle }$
with the class of pure sets in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. So V can see precisely how it is copied into
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. So V can see precisely how it is copied into
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Conversely, using the
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. Conversely, using the
![]() $\smash {\vec {{\mathbb A}}}$
enumeration, the structure
$\smash {\vec {{\mathbb A}}}$
enumeration, the structure
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
can see precisely how it is constructed from the pure sets by the interpretation we have provided. So this is a bi-interpretation.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
can see precisely how it is constructed from the pure sets by the interpretation we have provided. So this is a bi-interpretation.
In light of these various bi-interpretations, we are justified in viewing these interpreted models of urelement set theory from two perspectives. On the one hand,
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is a definable class in the ground model V, defined there as an interpreted class structure. On the other hand, since V is isomorphic to the pure sets of
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is a definable class in the ground model V, defined there as an interpreted class structure. On the other hand, since V is isomorphic to the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, we can view the model instead as an extension
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, we can view the model instead as an extension
![]() $V({\mkern 3.5mu\overline {\mkern -3.5mu A\mkern -.5mu}\mkern .5mu})$
of the original universe V, obtained by adjoining a new class
$V({\mkern 3.5mu\overline {\mkern -3.5mu A\mkern -.5mu}\mkern .5mu})$
of the original universe V, obtained by adjoining a new class
![]() ${\mkern 3.5mu\overline {\mkern -3.5mu A\mkern -.5mu}\mkern .5mu}$
of urelements to V, enumerated by the class A. The bi-interpretation result explains exactly how these two perspectives are equivalent accounts of the same phenomenon.
${\mkern 3.5mu\overline {\mkern -3.5mu A\mkern -.5mu}\mkern .5mu}$
of urelements to V, enumerated by the class A. The bi-interpretation result explains exactly how these two perspectives are equivalent accounts of the same phenomenon.
Let us next record a further observation about the nature of the interpreted urelement structure.
Theorem 2.2. Assume ZF in V and A is a definable class. Then every set in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is equinumerous with a pure set there. In particular, if the axiom of choice holds in V, then it also holds in
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is equinumerous with a pure set there. In particular, if the axiom of choice holds in V, then it also holds in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
Proof Every set
![]() $\bar y={\left \langle 1,y\right \rangle }$
created in
$\bar y={\left \langle 1,y\right \rangle }$
created in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is equinumerous there with the pure set
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is equinumerous there with the pure set
![]() $\check y$
. So if AC holds in V, then since every pure set in
$\check y$
. So if AC holds in V, then since every pure set in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
can be well-ordered there, and these orders can be transferred to the sets
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
can be well-ordered there, and these orders can be transferred to the sets
![]() $\bar y$
in
$\bar y$
in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, establishing AC in
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, establishing AC in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
The hypothesis that every set is equinumerous with a pure set is philosophically significant with regard to structuralism, because it follows that every mathematical structure is isomorphic to a structure in the pure sets. A structuralist in the philosophy of mathematics could therefore take this as evidence that urelements are not needed in such a situation, since one can already realize all possible mathematical structure in the universe of pure sets. Alternatively, since one mathematician’s modus ponens is another’s modus tollens, the observation is evidence that in order for urelements to be helpful to us in the foundations of mathematics, we should want or expect to have sets of urelements that are not equinumerous with any pure set. In particular, this would require a denial of the axiom of choice, since every well-order is isomorphic to an ordinal, which is a pure set. Do we expect that there are collections of irreducible atomic mathematical objects that cannot in principle be placed into bijection with any pure set? That seems strange and wonderful, but the puzzle is that such kinds of urelements would be very different from the traditional urelement proposals, such as numbers and geometric points, both of which find equinumerosity with pure sets. So the philosophical task for the urelement supporters is to explain why we would need a foundational theory to accommodate strange and bizarre set of urelements, if the intended sets of urelements are tame.
Corollary 2.3. The theories ZFC and
![]() $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are A many atoms” are bi-interpretable, where A is any ZF-definable class. Similarly with
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are A many atoms” are bi-interpretable, where A is any ZF-definable class. Similarly with
![]() $\mathrm {ZF}$
and
$\mathrm {ZF}$
and
![]() $\mathrm {ZF}\vec {\mathrm {U}}+$
“there are A many atoms.”
$\mathrm {ZF}\vec {\mathrm {U}}+$
“there are A many atoms.”
What we mean is that the assertion “there are A many atoms” is expressed in the language with the urelement enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
by asserting that this predicate enumerates the urelements using the class A as it is defined in the class of pure sets of the
$\smash {\vec {{\mathbb A}}}$
by asserting that this predicate enumerates the urelements using the class A as it is defined in the class of pure sets of the
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
model. In particular, the following theories are bi-interpretable:
$\mathrm {ZFC}\vec {\mathrm {U}}$
model. In particular, the following theories are bi-interpretable:
-
(1) ZFC,
-
(2)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
 $\omega $
many atoms,”
$\omega $
many atoms,” -
(3)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
 ${\mathbb R}$
many atoms,”
${\mathbb R}$
many atoms,” -
(4)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
 $\aleph _{\omega ^2+5}$
many atoms,”
$\aleph _{\omega ^2+5}$
many atoms,” -
(5)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are
 $\mathord {\mathrm {Ord}}$
many atoms,”
$\mathord {\mathrm {Ord}}$
many atoms,” -
(6)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are V many atoms,”
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“there are V many atoms,”
where we express the theories in the language with the urelement enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
. The corresponding theories with ZFCU in place of
$\smash {\vec {{\mathbb A}}}$
. The corresponding theories with ZFCU in place of
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
also are bi-interpretable with each other and ZFC, and all the above theories, provided one allows a parameter—simply use a set parameter to enumerate the atoms, as explained in Theorem 2.5.
$\mathrm {ZFC}\vec {\mathrm {U}}$
also are bi-interpretable with each other and ZFC, and all the above theories, provided one allows a parameter—simply use a set parameter to enumerate the atoms, as explained in Theorem 2.5.
Proof of Corollary 2.3
The interpretation definitions used in the proof of Theorem 2.1 are uniform across models, and therefore provide bi-interpretations of these theories, not just model-by-model. The theories
![]() $\mathrm {ZFCU}$
and
$\mathrm {ZFCU}$
and
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
, in the case the urelements form a set, are bi-interpretable with parameters, since one need only fix the set-sized enumeration of the urelements.
$\mathrm {ZFC}\vec {\mathrm {U}}$
, in the case the urelements form a set, are bi-interpretable with parameters, since one need only fix the set-sized enumeration of the urelements.
It follows that
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
is not a tight theory in the sense of [Reference Enayat, van Eijck, Iemhoff and Joosten4, Reference Freire and Hamkins5], since it admits these distinct bi-interpretable extensions. A theory is tight when any extensions of it are bi-interpretable if and only if they are identical.
$\mathrm {ZFC}\vec {\mathrm {U}}$
is not a tight theory in the sense of [Reference Enayat, van Eijck, Iemhoff and Joosten4, Reference Freire and Hamkins5], since it admits these distinct bi-interpretable extensions. A theory is tight when any extensions of it are bi-interpretable if and only if they are identical.
Corollary 2.4.
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
is not tight.
$\mathrm {ZFC}\vec {\mathrm {U}}$
is not tight.
If the class of urelements is a set, then we can dispense with the need for the urelement predicates
![]() ${\mathbb A}$
and
${\mathbb A}$
and
![]() $\smash {\vec {{\mathbb A}}}$
in the interpretation, since the enumeration will in effect be one of the sets available in
$\smash {\vec {{\mathbb A}}}$
in the interpretation, since the enumeration will in effect be one of the sets available in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, which we can simply use as a parameter.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, which we can simply use as a parameter.
Theorem 2.5. Working in the ZF set-theoretic universe V, if A is a set, then the following class structures are bi-interpretable, allowing parameters:
-
(1)
 ${\left \langle V,\in \right \rangle }$
.
${\left \langle V,\in \right \rangle }$
. -
(2)
 ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}\right \rangle }$
. -
(3)
 ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
. -
(4)
 ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
.
Proof If A is a set in V, then the predicates
![]() ${\mathbb A}$
and
${\mathbb A}$
and
![]() $\smash {\vec {{\mathbb A}}}$
both amount to sets in
$\smash {\vec {{\mathbb A}}}$
both amount to sets in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, and so the latter three structures are bi-interpretable with those parameters. And we know
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, and so the latter three structures are bi-interpretable with those parameters. And we know
![]() ${\left \langle V,\in \right \rangle }$
is bi-interpretable with
${\left \langle V,\in \right \rangle }$
is bi-interpretable with
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
by Theorem 2.1.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
by Theorem 2.1.
Corollary 2.6. The following theories are parametrically bi-interpretable:
-
(1) ZFC,
-
(2)
 $\mathrm {ZFCU}+$
“the urelements form a set,”
$\mathrm {ZFCU}+$
“the urelements form a set,” -
(3)
 $\mathrm {ZFC}\vec {\mathrm {U}}+$
“the urelements form a set.”
$\mathrm {ZFC}\vec {\mathrm {U}}+$
“the urelements form a set.”
Similarly, the following theories are also parametrically bi-interpretable:
-
(4) ZF,
-
(5)
 $\mathrm {ZFU}+$
“the urelements are bijective with a pure set.”
$\mathrm {ZFU}+$
“the urelements are bijective with a pure set.”
Proof If the urelements form a set, then by the axiom of choice they are bijective with some pure set, and the property of being such a pure-set-enumeration of the urelements is definable. Any such parameter will enable the bi-interpretations of Theorem 2.5. That is, the theory can define a nonempty set of parameters, any one of which will work as a parameter for the bi-interpretation, and this is what it means to be parametrically bi-interpretable.
If A is a proper class, however, then it will turn out that
![]() ${\left \langle V,\in \right \rangle }$
is not bi-interpretable with
${\left \langle V,\in \right \rangle }$
is not bi-interpretable with
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
, even with parameters, although these structures are mutually interpretable and semi-bi-interpretable, meaning that V can identify its copy inside
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},{\mathbb A}\right \rangle }$
, even with parameters, although these structures are mutually interpretable and semi-bi-interpretable, meaning that V can identify its copy inside
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
Theorem 2.7. The following theories are mutually interpretable, but no two of them are bi-interpretable, even allowing parameters:
-
(1) ZFC,
-
(2) ZFCU,
-
(3)
 $\mathrm {ZFCU}+$
“the urelements form a proper class.”
$\mathrm {ZFCU}+$
“the urelements form a proper class.”
Meanwhile, ZFC is semi-bi-interpretable with these latter theories.
Proof The urelement theory in case (3) is expressed using the urelement predicate
![]() ${\mathbb A}$
. We have already provided the mutual interpretations, since from any model
${\mathbb A}$
. We have already provided the mutual interpretations, since from any model
![]() $V\models \mathrm {ZFC}$
we can interpret the model
$V\models \mathrm {ZFC}$
we can interpret the model
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
for any class A, and conversely in any model of ZFCU the class of pure sets is a model of ZFC. This mutual interpretation is actually a semi-bi-interpretation, since in any case, V can see how it is copied into the pure sets of
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
for any class A, and conversely in any model of ZFCU the class of pure sets is a model of ZFC. This mutual interpretation is actually a semi-bi-interpretation, since in any case, V can see how it is copied into the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
by the map
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
by the map
![]() $u\mapsto \check u$
. What is not generally possible for
$u\mapsto \check u$
. What is not generally possible for
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, with only the urelement predicate
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, with only the urelement predicate
![]() ${\mathbb A}$
and not urelement enumeration predicate
${\mathbb A}$
and not urelement enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
, is to define exactly how it arises from its pure sets.
$\smash {\vec {{\mathbb A}}}$
, is to define exactly how it arises from its pure sets.
Let us prove first that no model of theory (3) is bi-interpretable with a model of ZFC, even allowing parameters in the interpretations. Suppose toward contradiction that a model M of ZFCU with a proper class of urelements is bi-interpretable with a model N of ZFC. Thus, N is parametrically definably interpreted in M, and there is a copy
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
of M definably interpreted in N, such that M can parametrically define an isomorphism
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
of M definably interpreted in N, such that M can parametrically define an isomorphism
![]() $\tau :M\cong {\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, and so there is a copy
$\tau :M\cong {\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, and so there is a copy
![]() ${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
of N definably interpreted in
${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
of N definably interpreted in
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, such that N can parametrically define an isomorphism
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, such that N can parametrically define an isomorphism
![]() $\sigma :N\cong {\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
.
$\sigma :N\cong {\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
.
Since M is a model of ZFCU with a proper class of urelements, we can define an automorphism
![]() $\pi :M\cong M$
that fixes all the parameters used in defining the interpretations and the maps
$\pi :M\cong M$
that fixes all the parameters used in defining the interpretations and the maps
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
, but which moves some object u to
$\sigma $
, but which moves some object u to
![]() $\pi (u)\neq u$
. Since
$\pi (u)\neq u$
. Since
![]() $\pi $
fixes the parameters used in the interpretation, it follows that
$\pi $
fixes the parameters used in the interpretation, it follows that
![]() $\pi $
fixes N,
$\pi $
fixes N,
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
,
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
,
![]() ${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
,
${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
,
![]() $\tau $
, and
$\tau $
, and
![]() $\sigma $
as definable classes in M.
$\sigma $
as definable classes in M.
Since
![]() $\pi $
fixes N as a class, and it fixes the interpretations of the relations of N as classes, it follows that
$\pi $
fixes N as a class, and it fixes the interpretations of the relations of N as classes, it follows that
![]() $\pi \upharpoonright N$
is an automorphism of N as a ZFC model. Furthermore, because N can define
$\pi \upharpoonright N$
is an automorphism of N as a ZFC model. Furthermore, because N can define
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, which can define its version of
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, which can define its version of
![]() $\pi $
on
$\pi $
on
![]() ${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
, which N can pull back from
${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
, which N can pull back from
![]() ${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
to N, it follows that
${\mkern 3.5mu\overline {\mkern -3.5muN\mkern -.5mu}\mkern .5mu}$
to N, it follows that
![]() $\pi \upharpoonright N$
would be a definable automorphism of N in N. But ZFC is definably rigid, and so
$\pi \upharpoonright N$
would be a definable automorphism of N in N. But ZFC is definably rigid, and so
![]() $\pi $
must fix the elements of N pointwise. Consequently, it also fixes the elements of
$\pi $
must fix the elements of N pointwise. Consequently, it also fixes the elements of
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
pointwise. But now, since
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
pointwise. But now, since
![]() $\pi $
also fixes
$\pi $
also fixes
![]() $\tau $
as a class, it follows that if
$\tau $
as a class, it follows that if
![]() $\tau $
takes u to
$\tau $
takes u to
![]() $\bar u$
in
$\bar u$
in
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, then it must take
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, then it must take
![]() $\pi (u)$
to
$\pi (u)$
to
![]() $\pi (\bar u)$
, which is the same as
$\pi (\bar u)$
, which is the same as
![]() $\bar u$
, since this is in
$\bar u$
, since this is in
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
. Thus,
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
. Thus,
![]() $\tau $
takes two different objects
$\tau $
takes two different objects
![]() $u\neq \pi (u)$
of M to the same object
$u\neq \pi (u)$
of M to the same object
![]() $\bar u$
in
$\bar u$
in
![]() ${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, contradicting the assumption that it was an isomorphism.
${\mkern 3.5mu\overline {\mkern -3.5muM\mkern -.5mu}\mkern .5mu}$
, contradicting the assumption that it was an isomorphism.
To prove the theorem, now, suppose that ZFC were bi-interpretable with one of the other theories, allowing parameters. Since every model of ZFCU with a proper class of atoms is a model of both theories (2) and (3), it would meant that every model of theory (3) was parametrically bi-interpretable with a model of ZFC, which we just proved is impossible. So ZFC is not parametrically bi-interpretable with either theory (2) or theory (3).
It follows also that theories (2) and (3) are not parametrically bi-interpretable, for every model of ZFC is also a model of ZFCU, and we’ve argued that no such model is parametrically bi-interpretable with a model of theory (3).
The proof relied on the fact that ZFC models are definably rigid, but models of ZFCU with a proper class of urelements have lots of parametrically definable automorphisms, fixing any desired finite list of parameters. In this situation, there can be no bi-interpretation of models. The basic lesson is that there is a fundamental difference for interpretative power between the theories
![]() $\mathrm {ZFCU}$
and
$\mathrm {ZFCU}$
and
![]() $\mathrm {ZFC}\vec {\mathrm {U}}$
, between having the urelements merely as a class
$\mathrm {ZFC}\vec {\mathrm {U}}$
, between having the urelements merely as a class
![]() ${\mathbb A}$
versus having them as an explicit enumeration
${\mathbb A}$
versus having them as an explicit enumeration
![]() $\smash {\vec {{\mathbb A}}}$
by a class of pure sets. One can expect to achieve bi-interpretation of urelement set theory with urelement-free set theory only in the latter case, and otherwise it is the urelement-free theory with the stronger interpretative power, since V sees how it is copied to the pure sets of
$\smash {\vec {{\mathbb A}}}$
by a class of pure sets. One can expect to achieve bi-interpretation of urelement set theory with urelement-free set theory only in the latter case, and otherwise it is the urelement-free theory with the stronger interpretative power, since V sees how it is copied to the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, but
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
, but
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\in ,{\mathbb A}\right \rangle }$
cannot in general see how it arises from its pure sets.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\in ,{\mathbb A}\right \rangle }$
cannot in general see how it arises from its pure sets.
3 Reflection
Let us recall the first-order reflection phenomenon in set theory. The Lévy–Montague reflection theorem of ZF set theory asserts that for any formula
![]() $\varphi (x)$
, there is an ordinal
$\varphi (x)$
, there is an ordinal
![]() $\lambda $
such that
$\lambda $
such that
![]() $\varphi $
is absolute between
$\varphi $
is absolute between
![]() $V_{\lambda }$
and V. A somewhat more refined version asserts of every meta-theoretically finite number n that there is an ordinal
$V_{\lambda }$
and V. A somewhat more refined version asserts of every meta-theoretically finite number n that there is an ordinal
![]() $\lambda $
such that all
$\lambda $
such that all
![]() $\Sigma _n$
formulas are absolute between
$\Sigma _n$
formulas are absolute between
![]() $V_{\lambda }$
and V. Indeed, there is a definable closed unbounded class C of such ordinals
$V_{\lambda }$
and V. Indeed, there is a definable closed unbounded class C of such ordinals
![]() $\lambda $
, the club of
$\lambda $
, the club of
![]() $\Sigma _n$
-correct cardinals. This is a theorem scheme, with a separate statement for each number n. The reflection theorem is equivalent over the rest of ZFC to the collection axiom (hence to replacement over Zermelo set theory), since the existence of sufficiently large reflecting ordinals
$\Sigma _n$
-correct cardinals. This is a theorem scheme, with a separate statement for each number n. The reflection theorem is equivalent over the rest of ZFC to the collection axiom (hence to replacement over Zermelo set theory), since the existence of sufficiently large reflecting ordinals
![]() $\lambda $
provides
$\lambda $
provides
![]() $V_{\lambda }$
as a suitable collecting set for the formula asserting that indeed the witnesses exist.
$V_{\lambda }$
as a suitable collecting set for the formula asserting that indeed the witnesses exist.

In the urelement context, when there are a proper class of urelements, then we should not generally expect to reflect truths from
![]() $V(A)$
specifically to the class
$V(A)$
specifically to the class
![]() $V_{\lambda }(A)$
, since there will be sets of urelements
$V_{\lambda }(A)$
, since there will be sets of urelements
![]() $w\subseteq A$
in
$w\subseteq A$
in
![]() $V(A)$
of cardinality larger than
$V(A)$
of cardinality larger than
![]() $\lambda $
, which having rank
$\lambda $
, which having rank
![]() $1$
will be in
$1$
will be in
![]() $V_{\lambda }(A)$
, but such w are not equinumerous with any ordinal in
$V_{\lambda }(A)$
, but such w are not equinumerous with any ordinal in
![]() $V_{\lambda }(A)$
. This would be a violation of reflection between
$V_{\lambda }(A)$
. This would be a violation of reflection between
![]() $V_{\lambda }(A)$
and
$V_{\lambda }(A)$
and
![]() $V(A)$
for the statement
$V(A)$
for the statement
![]() $\varphi =$
“every set of urelements is bijective with an ordinal.” What we should want to do with reflection, rather than reflecting specifically to some rank-initial-segment class
$\varphi =$
“every set of urelements is bijective with an ordinal.” What we should want to do with reflection, rather than reflecting specifically to some rank-initial-segment class
![]() $V_{\lambda }(A)$
, is to reflect truth to some transitive set.
$V_{\lambda }(A)$
, is to reflect truth to some transitive set.
Definition 3.1. The first-order reflection principle is the scheme of assertions that for every set p and every particular formula
![]() $\varphi $
in the first-order language of urelement set theory there is a transitive set v containing p such that
$\varphi $
in the first-order language of urelement set theory there is a transitive set v containing p such that
![]() $\varphi $
is absolute between v and
$\varphi $
is absolute between v and
![]() $V(A)$
.
$V(A)$
.
If there is merely a set of urelements, then we can stratify the full universe
![]() $V(A)$
by the rank hierarchy
$V(A)$
by the rank hierarchy
![]() $V_{\alpha }(A)$
, and each of these is a set. This provides a set-like continuous transfinite tower
$V_{\alpha }(A)$
, and each of these is a set. This provides a set-like continuous transfinite tower
![]() $V_{\alpha }(A)$
, and this is enough to run the usual ZFC proof of the reflection theorem, where we shall be able to reflect any
$V_{\alpha }(A)$
, and this is enough to run the usual ZFC proof of the reflection theorem, where we shall be able to reflect any
![]() $\varphi $
from
$\varphi $
from
![]() $V(A)$
to some
$V(A)$
to some
![]() $v=V_{\alpha }(A)$
. Similarly, in a model of
$v=V_{\alpha }(A)$
. Similarly, in a model of
![]() $\mathrm {ZFC}\vec {\mathrm {U}}+ \text {“}\mathord {\mathrm {Ord}}$
many atoms,” we can similarly stratify the universe in a set-like hierarchy, using
$\mathrm {ZFC}\vec {\mathrm {U}}+ \text {“}\mathord {\mathrm {Ord}}$
many atoms,” we can similarly stratify the universe in a set-like hierarchy, using
![]() $V_{\alpha +1}(\smash {\vec {{\mathbb A}}}\upharpoonright \alpha )$
, where
$V_{\alpha +1}(\smash {\vec {{\mathbb A}}}\upharpoonright \alpha )$
, where
![]() $\smash {\vec {{\mathbb A}}}\upharpoonright \alpha $
restricts the urelement enumeration to the first
$\smash {\vec {{\mathbb A}}}\upharpoonright \alpha $
restricts the urelement enumeration to the first
![]() $\alpha $
many elements, and taking unions at limit ordinals for continuity. This continuous cumulative hierarchy is again enough to prove the reflection theorem by the usual argument, reflecting any
$\alpha $
many elements, and taking unions at limit ordinals for continuity. This continuous cumulative hierarchy is again enough to prove the reflection theorem by the usual argument, reflecting any
![]() $\varphi $
from
$\varphi $
from
![]() $V(A)$
to some
$V(A)$
to some
![]() $v=\bigcup _{\alpha <\lambda }V_{\alpha +1}(\smash {\vec {{\mathbb A}}}\upharpoonright \alpha )$
.
$v=\bigcup _{\alpha <\lambda }V_{\alpha +1}(\smash {\vec {{\mathbb A}}}\upharpoonright \alpha )$
.

But in fact, we should like to prove that we get the first-order reflection theorem in ZFCU generally, making no assumption on the number or kinds of urelements. Let’s begin by establishing the following duplication and homogeneity lemmas, showing that over some fixed set of urelements, all additional sets of urelements of the same cardinality look exactly alike.
Lemma 3.2 (Urelement duplication)
Assume ZFU plus every set of urelements is well-orderable. Then there is a set u, such that every set of urelements w disjoint from u can be duplicated, that is, w is equinumerous with some set of urelements
![]() $w'$
disjoint from both u and w.
$w'$
disjoint from both u and w.
Proof Assume ZFU plus every set of urelements is well-orderable, and let u be any set of urelements for which the supremum of the sizes of the sets of urelements w disjoint from u is as small as possible. (Perhaps this supremum is unbounded in the cardinals, and that will be fine.) Notice that if every cardinal
![]() $\gamma $
in some set of cardinals is realized by a set of urelements disjoint from u, then we can collect such sets together and thereby realize a cardinal at least as great as each of them. It follows by the choice of u that if w is a set of urelements disjoint from u, then we must be able to realize this cardinal again disjoint from
$\gamma $
in some set of cardinals is realized by a set of urelements disjoint from u, then we can collect such sets together and thereby realize a cardinal at least as great as each of them. It follows by the choice of u that if w is a set of urelements disjoint from u, then we must be able to realize this cardinal again disjoint from
![]() $u\cup w$
, for otherwise
$u\cup w$
, for otherwise
![]() $u\cup w$
would have served as a better choice than u. Thus, we have fulled the duplication property.
$u\cup w$
would have served as a better choice than u. Thus, we have fulled the duplication property.
The urelement duplication property will not necessarily hold over any set u, since in the model Y discussed earlier, the uncountable set A of urelements cannot be duplicated to a disjoint set of urelements of the same size, since all the remaining sets of urelements are countable subsets of B, and so in that model Y, we do not achieve duplication over
![]() $\varnothing $
. In the model Y, however, we do achieve the duplication property over the set
$\varnothing $
. In the model Y, however, we do achieve the duplication property over the set
![]() $u=A$
, since any set w disjoint from this u can be duplicated to another such set
$u=A$
, since any set w disjoint from this u can be duplicated to another such set
![]() $w'$
disjoint from
$w'$
disjoint from
![]() $u\cup w$
. Moreover, the second author [Reference Yao26] proves that it is consistent with ZFU +
$u\cup w$
. Moreover, the second author [Reference Yao26] proves that it is consistent with ZFU +
![]() $\omega $
-DC that the duplication property holds over no set of urelements.
$\omega $
-DC that the duplication property holds over no set of urelements.
Lemma 3.3 (Urelement duplication
 $\to $
homogeneity)
$\to $
homogeneity)
Assume ZFU. If all sets of urelements disjoint from u can be duplicated, then any two equinumerous such sets w and
![]() $w'$
are automorphic over u—there is an automorphism of the universe
$w'$
are automorphic over u—there is an automorphism of the universe
![]() $V(A)$
swapping w with
$V(A)$
swapping w with
![]() $w'$
and fixing every element of u.
$w'$
and fixing every element of u.
Proof Assume ZFU and sets of urelements disjoint from u can be duplicated. Suppose that w and
![]() $w'$
are equinumerous and disjoint from u. If w and
$w'$
are equinumerous and disjoint from u. If w and
![]() $w'$
are disjoint, then the equinumerosity produces a permutation
$w'$
are disjoint, then the equinumerosity produces a permutation
![]() $\pi $
of the union
$\pi $
of the union
![]() $v=w\cup w'$
. This permutation extends to a permutation
$v=w\cup w'$
. This permutation extends to a permutation
![]() $\pi :A\to A$
of the class of all urelements by fixing all other urelements—in particular, fixing every element of u—and this permutation generates an automorphism
$\pi :A\to A$
of the class of all urelements by fixing all other urelements—in particular, fixing every element of u—and this permutation generates an automorphism
![]() $\pi :V(A)\to V(A)$
showing that w and
$\pi :V(A)\to V(A)$
showing that w and
![]() $w'$
are automorphic over u, as desired.
$w'$
are automorphic over u, as desired.
But perhaps w and
![]() $w'$
are not disjoint. By the duplication property, however, there is another set disjoint from
$w'$
are not disjoint. By the duplication property, however, there is another set disjoint from
![]() $u\cup w\cup w'$
that is equinumerous with
$u\cup w\cup w'$
that is equinumerous with
![]() $w\cup w'$
, and in particular, there is a set
$w\cup w'$
, and in particular, there is a set
![]() $w''$
disjoint from
$w''$
disjoint from
![]() $u\cup w\cup w'$
equinumerous with w. So w is automorphic with
$u\cup w\cup w'$
equinumerous with w. So w is automorphic with
![]() $w''$
over u by the previous paragraph, and also
$w''$
over u by the previous paragraph, and also
![]() $w''$
is automorphic to
$w''$
is automorphic to
![]() $w'$
. By composing these automorphisms, we see that w is automorphic to
$w'$
. By composing these automorphisms, we see that w is automorphic to
![]() $w'$
.
$w'$
.
We cannot in general dispense with the fixed set u in the homogeneity claim of Lemma 3.3, for although as we have observed
![]() $V(B)$
is isomorphic to
$V(B)$
is isomorphic to
![]() $V(C)$
whenever B and C are equinumerous classes of urelements, such an isomorphism is not necessarily realizable by an automorphism of
$V(C)$
whenever B and C are equinumerous classes of urelements, such an isomorphism is not necessarily realizable by an automorphism of
![]() $V(A)$
. Indeed, it is not true in general in ZFCU that whenever two sets of urelements are equinumerous, then they are automorphic, since perhaps there are exactly
$V(A)$
. Indeed, it is not true in general in ZFCU that whenever two sets of urelements are equinumerous, then they are automorphic, since perhaps there are exactly
![]() $\omega _1$
many urelements and w is the set of all urelements, but
$\omega _1$
many urelements and w is the set of all urelements, but
![]() $w'$
has all but one of them. These sets are equinumerous by a bijection in
$w'$
has all but one of them. These sets are equinumerous by a bijection in
![]() $V(w)$
and
$V(w)$
and
![]() $V(w)$
is isomorphic to
$V(w)$
is isomorphic to
![]() $V(w')$
, but the sets are not automorphic by any automorphism of
$V(w')$
, but the sets are not automorphic by any automorphism of
![]() $V(w)$
.
$V(w)$
.
-
(1) ZFCU proves the
 $\omega $
-dependent choice scheme
$\omega $
-dependent choice scheme
 $\omega $
-DC.Footnote
2
$\omega $
-DC.Footnote
2
-
(2) ZFCU proves the first-order reflection principle scheme.
Proof Assume ZFCU holds in
![]() $V(A)$
, where V is the class of pure sets and A is the class of atoms. Let us first prove the
$V(A)$
, where V is the class of pure sets and A is the class of atoms. Let us first prove the
![]() $\omega $
-DC scheme. Suppose that R is a definable class relation on a definable class X, such that every
$\omega $
-DC scheme. Suppose that R is a definable class relation on a definable class X, such that every
![]() $x\in X$
has at least one
$x\in X$
has at least one
![]() $y\in X$
such that
$y\in X$
such that
![]() $x\mathrel {R}y$
. We want to prove that there is an
$x\mathrel {R}y$
. We want to prove that there is an
![]() $\omega $
-sequence threading the relation. Fix a parameter p that is sufficient for the definitions of X and R.
$\omega $
-sequence threading the relation. Fix a parameter p that is sufficient for the definitions of X and R.
We define a certain increasing sequence of cardinals
![]() $\lambda _0<\lambda _1<\lambda _2<\cdots $
by recursion. Fix a set u as in Lemmas 3.2 and 3.3, so that every pair of equinumerous sets of urelements outside u are automorphic over u. We may assume that p has support in u. Let
$\lambda _0<\lambda _1<\lambda _2<\cdots $
by recursion. Fix a set u as in Lemmas 3.2 and 3.3, so that every pair of equinumerous sets of urelements outside u are automorphic over u. We may assume that p has support in u. Let
![]() $\lambda _0$
be the least cardinal such that X has an element inside
$\lambda _0$
be the least cardinal such that X has an element inside
![]() $V_{\lambda _0}(w)$
for some set w extending u of size less than
$V_{\lambda _0}(w)$
for some set w extending u of size less than
![]() $\lambda _0$
. If
$\lambda _0$
. If
![]() $\lambda _n$
is defined, let
$\lambda _n$
is defined, let
![]() $\lambda _{n+1}$
be least above
$\lambda _{n+1}$
be least above
![]() $\lambda _n$
such that whenever
$\lambda _n$
such that whenever
![]() $x\in X\cap V_{\lambda _n}(w)$
, where w is a set of urelements extending u of size less than
$x\in X\cap V_{\lambda _n}(w)$
, where w is a set of urelements extending u of size less than
![]() $\lambda _n$
, and there is a y with
$\lambda _n$
, and there is a y with
![]() $x\mathrel {R} y$
, then there is such a y inside
$x\mathrel {R} y$
, then there is such a y inside
![]() $V_{\lambda _{n+1}}(w^+)$
, where
$V_{\lambda _{n+1}}(w^+)$
, where
![]() $w^+$
is an extension of w of size less than
$w^+$
is an extension of w of size less than
![]() $\lambda _{n+1}$
. This cardinal exists since all such
$\lambda _{n+1}$
. This cardinal exists since all such
![]() $V_{\lambda _n}(w)$
are automorphic in
$V_{\lambda _n}(w)$
are automorphic in
![]() $V(A)$
, once the number of urelements beyond u is fixed, and so there are only a set of possible w to consider, and consequently a set of possible x to consider. Now let
$V(A)$
, once the number of urelements beyond u is fixed, and so there are only a set of possible w to consider, and consequently a set of possible x to consider. Now let
![]() $\lambda =\sup _n\lambda _n$
.
$\lambda =\sup _n\lambda _n$
.
By the collection axiom, we can consider the possible cardinalities of sets of urelements and then take the union of a family of such sets realizing all possible cardinalities below
![]() $\lambda $
, and thereby find a set
$\lambda $
, and thereby find a set
![]() $\bar w$
of urelements extending u, which is at least as large as any set of urelements of size less than
$\bar w$
of urelements extending u, which is at least as large as any set of urelements of size less than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $v=\bigcup _{w\subseteq \bar w,\,|w|<\lambda } V_{\lambda }(w)$
, where we range over all
$v=\bigcup _{w\subseteq \bar w,\,|w|<\lambda } V_{\lambda }(w)$
, where we range over all
![]() $w\subseteq \bar w$
of size less than
$w\subseteq \bar w$
of size less than
![]() $\lambda $
. Notice that if
$\lambda $
. Notice that if
![]() $x\in X\cap v$
, then x is in some
$x\in X\cap v$
, then x is in some
![]() $V_{\lambda _n}(w)$
for some
$V_{\lambda _n}(w)$
for some
![]() $w\subseteq \bar w$
of size less than
$w\subseteq \bar w$
of size less than
![]() $\lambda _n$
, and consequently there is
$\lambda _n$
, and consequently there is
![]() $y\in V_{\lambda _{n+1}}(w')$
for some such
$y\in V_{\lambda _{n+1}}(w')$
for some such
![]() $w'$
of size less than
$w'$
of size less than
![]() $\lambda _{n+1}$
, and by homogeneity we may assume
$\lambda _{n+1}$
, and by homogeneity we may assume
![]() $w'\subseteq \bar w$
. In short, v has R-successors for each of its elements in X.
$w'\subseteq \bar w$
. In short, v has R-successors for each of its elements in X.
It now follows easily by the axiom of choice that we may thread R. We simply well-order the set v and then choose the least successor: fix any
![]() $x_0\in X\cap v$
, and let
$x_0\in X\cap v$
, and let
![]() $x_{n+1}$
be least in v such that
$x_{n+1}$
be least in v such that
![]() $x_n\mathrel {R}x_{n+1}$
. So
$x_n\mathrel {R}x_{n+1}$
. So
![]() ${\left \langle x_n\mid n<\omega \right \rangle }$
threads the relation and we have proved the
${\left \langle x_n\mid n<\omega \right \rangle }$
threads the relation and we have proved the
![]() $\omega $
-DC scheme.
$\omega $
-DC scheme.
Next, we observe that the
![]() $\omega $
-DC scheme suffices to establish every instance of the first-order reflection principle. Fix any formula
$\omega $
-DC scheme suffices to establish every instance of the first-order reflection principle. Fix any formula
![]() $\varphi $
in the language of urelement set theory, using
$\varphi $
in the language of urelement set theory, using
![]() $\in $
and the urelement predicate
$\in $
and the urelement predicate
![]() ${\mathbb A}$
, and list the subformulas
${\mathbb A}$
, and list the subformulas
![]() $\varphi _0,\ldots ,\varphi _k$
. Define
$\varphi _0,\ldots ,\varphi _k$
. Define
![]() $u\mathrel {R} v$
for sets
$u\mathrel {R} v$
for sets
![]() $u,v$
if for every
$u,v$
if for every
![]() $\vec x$
from u, if there is a witness y in
$\vec x$
from u, if there is a witness y in
![]() $V(A)$
such that
$V(A)$
such that
![]() $\varphi _i(\vec x,y)$
, then there is such a
$\varphi _i(\vec x,y)$
, then there is such a
![]() $y\in v$
. In other words, the set v contains witnesses for the objects in u, if there are any such objects. By the collection axiom scheme, every set u is related to some set v, and so by the principle
$y\in v$
. In other words, the set v contains witnesses for the objects in u, if there are any such objects. By the collection axiom scheme, every set u is related to some set v, and so by the principle
![]() $\omega $
-DC, there is a threading sequence
$\omega $
-DC, there is a threading sequence
![]() ${\left \langle u_n\mid n<\omega \right \rangle }$
, such that
${\left \langle u_n\mid n<\omega \right \rangle }$
, such that
![]() $u_n\mathrel {R}u_{n+1}$
for every n. It follows that the union set
$u_n\mathrel {R}u_{n+1}$
for every n. It follows that the union set
![]() $u=\bigcup _n u_n$
is closed under witnesses for all the
$u=\bigcup _n u_n$
is closed under witnesses for all the
![]() $\varphi _i$
, and it follows by the Tarski–Vaught criterion that
$\varphi _i$
, and it follows by the Tarski–Vaught criterion that
![]() $\varphi $
and all subformulas are absolute between u and
$\varphi $
and all subformulas are absolute between u and
![]() $V(A)$
, as desired. And we could have accommodated any particular set simply by starting with a sufficient
$V(A)$
, as desired. And we could have accommodated any particular set simply by starting with a sufficient
![]() $u_0$
.
$u_0$
.
3.1 Reflection without choice
Perhaps the reader is surprised that our proof of first-order reflection for urelement set theory made use of the axiom of choice, since in the ZF context, one proves the Lévy–Montague reflection theorem without any appeal to the axiom of choice. Does the reflection principle hold in ZFU? We don’t yet know the full answer, but we can prove reflection in several weaker contexts than full ZFCU. So let us take a small detour in this subsection to do so.
Theorem 3.5. Assume ZFU. If there is a set u such that
-
(1) every set of urelements is equinumerous with some set in
 $V(u)$
and
$V(u)$
and -
(2) homogeneity holds over u—all equinumerous sets of urelements disjoint from u are automorphic,
then the first-order reflection principle holds.
In light of Lemma 3.3, which shows that urelement duplication implies homogeneity, it suffices to have urelement duplication over u in place of homogeneity in this theorem. The first hypothesis can be equivalently stated as:
![]() $V(u)$
realizes all cardinalities—every set is equinumerous with a set in
$V(u)$
realizes all cardinalities—every set is equinumerous with a set in
![]() $V(u)$
. As we mentioned earlier, such a hypothesis is relevant for philosophical issues in urelement set theory as a foundation of mathematics, because
$V(u)$
. As we mentioned earlier, such a hypothesis is relevant for philosophical issues in urelement set theory as a foundation of mathematics, because
![]() $V(u)$
would have isomorphic copies of every possible mathematical structure.
$V(u)$
would have isomorphic copies of every possible mathematical structure.
Notice that the two hypotheses of the theorem hold in the theory
![]() $\mathrm {ZFU}+$
“there are
$\mathrm {ZFU}+$
“there are
![]() $\mathord {\mathrm {Ord}}$
many atoms” and also in “there are V many atoms” and “there is a set u such that there are
$\mathord {\mathrm {Ord}}$
many atoms” and also in “there are V many atoms” and “there is a set u such that there are
![]() $V(u)$
many atoms” and these theories can each arise with the pure sets being an arbitrary model of ZF, with very bad failures of the axiom of choice.
$V(u)$
many atoms” and these theories can each arise with the pure sets being an arbitrary model of ZF, with very bad failures of the axiom of choice.
Proof Assume ZFU and fix the set u for which every set of urelements is equinumerous with a set in
![]() $V(u)$
and the homogeneity principle holds over u. We proceed similarly to the argument of Theorem 3.4, but avoiding the need for the axiom of choice. Fix any set p and formula
$V(u)$
and the homogeneity principle holds over u. We proceed similarly to the argument of Theorem 3.4, but avoiding the need for the axiom of choice. Fix any set p and formula
![]() $\varphi $
and enumerate the subformulas
$\varphi $
and enumerate the subformulas
![]() $\varphi _0,\ldots ,\varphi _k$
as before. We define an increasing sequence of cardinals
$\varphi _0,\ldots ,\varphi _k$
as before. We define an increasing sequence of cardinals
![]() $\lambda _0<\lambda _1<\cdots $
as before. Let
$\lambda _0<\lambda _1<\cdots $
as before. Let
![]() $\lambda _0$
be any cardinal (and enlarge u if necessary) so that any desired parameters appear in
$\lambda _0$
be any cardinal (and enlarge u if necessary) so that any desired parameters appear in
![]() $V_{\lambda _0}(u)$
. If
$V_{\lambda _0}(u)$
. If
![]() $\lambda _n$
is defined, let
$\lambda _n$
is defined, let
![]() $\lambda _{n+1}$
be the least cardinal above
$\lambda _{n+1}$
be the least cardinal above
![]() $\lambda _n$
such that if
$\lambda _n$
such that if
![]() $\vec x$
is a finite tuple from
$\vec x$
is a finite tuple from
![]() $V_{\lambda _n}(w)$
, where w is a set of urelements equinumerous with some set in
$V_{\lambda _n}(w)$
, where w is a set of urelements equinumerous with some set in
![]() $V_{\lambda _n}(u)$
and there is a y for which
$V_{\lambda _n}(u)$
and there is a y for which
![]() $\varphi _i(\vec x,y)$
, then there is such a y in
$\varphi _i(\vec x,y)$
, then there is such a y in
![]() $V_{\lambda _{n+1}}(w^+)$
, where
$V_{\lambda _{n+1}}(w^+)$
, where
![]() $w^+$
is an extension of w that is equinumerous with some set in
$w^+$
is an extension of w that is equinumerous with some set in
![]() $V_{\lambda _{n+1}}(u)$
. Such a cardinal exists, since all such
$V_{\lambda _{n+1}}(u)$
. Such a cardinal exists, since all such
![]() $w^+$
are automorphic over u, once the size beyond u is fixed, and so there are only a set of possible
$w^+$
are automorphic over u, once the size beyond u is fixed, and so there are only a set of possible
![]() $\vec x$
to consider. Let
$\vec x$
to consider. Let
![]() $\lambda =\sup _n\lambda _n$
.
$\lambda =\sup _n\lambda _n$
.
As before, we can consider the sets in
![]() $V_{\lambda }(u)$
that are the cardinalities of a set of urelements and apply collection to collect a family of such sets of urelements. The union of that collecting set will be a set
$V_{\lambda }(u)$
that are the cardinalities of a set of urelements and apply collection to collect a family of such sets of urelements. The union of that collecting set will be a set
![]() $\bar w$
of urelements, whose size is at least as large as any set of urelements equinumerous with an element of
$\bar w$
of urelements, whose size is at least as large as any set of urelements equinumerous with an element of
![]() $V_{\lambda }(u)$
. Notice that the sets of urelements equinumerous with a set in
$V_{\lambda }(u)$
. Notice that the sets of urelements equinumerous with a set in
![]() $V_{\lambda }(u)$
are closed under finite unions, since if w and
$V_{\lambda }(u)$
are closed under finite unions, since if w and
![]() $w'$
are isomorphic respectively with x and
$w'$
are isomorphic respectively with x and
![]() $x'$
in
$x'$
in
![]() $V_{\lambda }(u)$
, then by using pairs we may assume x and
$V_{\lambda }(u)$
, then by using pairs we may assume x and
![]() $x'$
are disjoint, and so
$x'$
are disjoint, and so
![]() $w\cup w'$
will be equinumerous with a subset of
$w\cup w'$
will be equinumerous with a subset of
![]() $x\cup x'$
, which is in
$x\cup x'$
, which is in
![]() $V_{\lambda }(u)$
. Let
$V_{\lambda }(u)$
. Let
![]() $v=\bigcup _{w\subseteq \bar w}V_{\lambda }(w)$
, where we allow
$v=\bigcup _{w\subseteq \bar w}V_{\lambda }(w)$
, where we allow
![]() $w\subseteq \bar w$
that are equinumerous with a set in
$w\subseteq \bar w$
that are equinumerous with a set in
![]() $V_{\lambda }(u)$
. This set v is a transitive set which is closed under witnesses for the formulas
$V_{\lambda }(u)$
. This set v is a transitive set which is closed under witnesses for the formulas
![]() $\varphi _i$
, since if
$\varphi _i$
, since if
![]() $\vec x$
is in v and there is a y with
$\vec x$
is in v and there is a y with
![]() $\varphi _i(\vec x,y)$
, then since
$\varphi _i(\vec x,y)$
, then since
![]() $\vec x\in V_{\lambda _n}(w)$
for some
$\vec x\in V_{\lambda _n}(w)$
for some
![]() $w\subseteq \bar w$
of size equinumerous with a set in
$w\subseteq \bar w$
of size equinumerous with a set in
![]() $V_{\lambda _n}$
, then we will be able to find such a y in
$V_{\lambda _n}$
, then we will be able to find such a y in
![]() $V_{\lambda _{n+1}}(w^+)$
, for a suitable size
$V_{\lambda _{n+1}}(w^+)$
, for a suitable size
![]() $w^+\subseteq \bar w$
, making
$w^+\subseteq \bar w$
, making
![]() $y\in v$
. So by the Tarski–Vaught criterion, it follows that
$y\in v$
. So by the Tarski–Vaught criterion, it follows that
![]() $\varphi $
is absolute between v and
$\varphi $
is absolute between v and
![]() $V(A)$
, as desired.
$V(A)$
, as desired.
The following corollary is an immediate consequence.
Corollary 3.6. Assume ZFU. If every set of urelements is equinumerous with a pure set and all sets of urelements can be duplicated over some set u, then the first-order reflection principle holds.
In particular, the theory
![]() $\mathrm {ZFU}+$
“every set of urelements is well-orderable” implies the first-order reflection principle, because all well-orderable sets are equinumerous with an ordinal, which is a pure set, and Lemma 3.2 provides a set u over which sets of urelements can be duplicated. The assumption that every set of urelements is well-orderable is strictly weaker than AC over ZFU, since if one begins in a ZF set-theoretic universe V without AC, but interprets
$\mathrm {ZFU}+$
“every set of urelements is well-orderable” implies the first-order reflection principle, because all well-orderable sets are equinumerous with an ordinal, which is a pure set, and Lemma 3.2 provides a set u over which sets of urelements can be duplicated. The assumption that every set of urelements is well-orderable is strictly weaker than AC over ZFU, since if one begins in a ZF set-theoretic universe V without AC, but interprets
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
for a well-orderable class A, such as
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
for a well-orderable class A, such as
![]() $A=\mathord {\mathrm {Ord}}$
, then every set of urelements in
$A=\mathord {\mathrm {Ord}}$
, then every set of urelements in
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will be well-orderable there, but AC will still fail amongst the pure sets. For example, it is relatively consistent with ZFU to have a class of urelements enumerated by the ordinals, yet still
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will be well-orderable there, but AC will still fail amongst the pure sets. For example, it is relatively consistent with ZFU to have a class of urelements enumerated by the ordinals, yet still
![]() ${\mathbb R}$
has no well-order. For the same reason, the assertion that every set of urelements is well-orderable is strictly weaker than the assertion that the class of all urelements has a definable well-order, since one cannot define a class well-order of the model
${\mathbb R}$
has no well-order. For the same reason, the assertion that every set of urelements is well-orderable is strictly weaker than the assertion that the class of all urelements has a definable well-order, since one cannot define a class well-order of the model
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\in ,{\mathbb A}\right \rangle }$
, as there will be nontrivial automorphisms of this structure swapping urelements beyond the support of any parameters used in the definition, and these would not fix the well-order. Indeed, the urelements of this model can have no definable linear order.
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\in ,{\mathbb A}\right \rangle }$
, as there will be nontrivial automorphisms of this structure swapping urelements beyond the support of any parameters used in the definition, and these would not fix the well-order. Indeed, the urelements of this model can have no definable linear order.
Let us also prove that we get reflection for free whenever we construct a model of ZFU by interpreting from a given model in which reflection holds. This includes every model of ZF, and so all the interpreted models
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will have reflection.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
will have reflection.
Theorem 3.7. Assume ZFU. If the universe
![]() $V(A)$
is interpretable in the class V of pure sets, then the first-order reflection principle holds. More generally, if
$V(A)$
is interpretable in the class V of pure sets, then the first-order reflection principle holds. More generally, if
![]() $V(A)$
is interpretable in a set-like manner inside a definable transitive class
$V(A)$
is interpretable in a set-like manner inside a definable transitive class
![]() $W\subseteq V(A)$
containing all pure sets and satisfying ZFU plus the reflection principle, then
$W\subseteq V(A)$
containing all pure sets and satisfying ZFU plus the reflection principle, then
![]() $V(A)$
also satisfies the reflection principle.
$V(A)$
also satisfies the reflection principle.
Proof Assume the ZFU universe
![]() $V(A)$
is interpretable inside a definable transitive class
$V(A)$
is interpretable inside a definable transitive class
![]() $W\models \mathrm {ZFU}$
containing the pure sets in which the reflection principle holds, and that the interpreted membership relation
$W\models \mathrm {ZFU}$
containing the pure sets in which the reflection principle holds, and that the interpreted membership relation
![]() $\in ^{V(A)}$
is set-like in W. Fix the definition
$\in ^{V(A)}$
is set-like in W. Fix the definition
![]() $\psi $
for the interpretation of
$\psi $
for the interpretation of
![]() $V(A)$
inside W. For any statement
$V(A)$
inside W. For any statement
![]() $\varphi $
true in
$\varphi $
true in
![]() $V(A)$
, consider the more complex statement, “
$V(A)$
, consider the more complex statement, “
![]() $\varphi $
holds in the interpreted model defined by
$\varphi $
holds in the interpreted model defined by
![]() $\psi $
.” By reflection in W, there is a transitive set v in W for which
$\psi $
.” By reflection in W, there is a transitive set v in W for which
![]() $\varphi $
is absolute between
$\varphi $
is absolute between
![]() $V(A)$
and the corresponding set-sized version of the universe
$V(A)$
and the corresponding set-sized version of the universe
![]() $V(A)$
as interpreted in v, that is, v’s version of
$V(A)$
as interpreted in v, that is, v’s version of
![]() $V(A)$
. We can ensure that this is a transitive set in the interpreted copy of
$V(A)$
. We can ensure that this is a transitive set in the interpreted copy of
![]() $V(A)$
by also asking v to be closed under all the
$V(A)$
by also asking v to be closed under all the
![]() $V(A)$
-members of its elements, using that the interpreted relation is set-like in W. Thus, we found a transitive set in
$V(A)$
-members of its elements, using that the interpreted relation is set-like in W. Thus, we found a transitive set in
![]() $V(A)$
to which
$V(A)$
to which
![]() $\varphi $
reflects.
$\varphi $
reflects.
For example, perhaps V is a model of ZF in which the reals are not well-orderable, say, but we can nevertheless interpret the model
![]() $V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
with an urelement for every pure set, thereby satisfying
$V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
with an urelement for every pure set, thereby satisfying
![]() $\mathrm {ZFU}+$
“there are V many urelements.” Theorem 3.7 shows that the resulting model
$\mathrm {ZFU}+$
“there are V many urelements.” Theorem 3.7 shows that the resulting model
![]() $V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
will fulfill the first-order reflection principle. This conclusion also follows from Theorem 3.6, since every set in
$V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
will fulfill the first-order reflection principle. This conclusion also follows from Theorem 3.6, since every set in
![]() $V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
is equinumerous with a pure set and every set of urelements can be duplicated in this model.
$V{\mathopen {\lbrack \!\lbrack }V\mathclose {\rbrack \!\rbrack }}$
is equinumerous with a pure set and every set of urelements can be duplicated in this model.
4 Class theory
We should like next to undertake the entire analysis in the context of second-order set theory, developing the urelement analogues of Gödel–Bernays set theory and Kelley–Morse set theory. These are conveniently formalized as two-sorted theories, with a first-order domain of individuals, consisting of the atoms and the sets, and a second-order domain of classes, consisting of a family of classes of individuals.
Let us begin with a quick review of the second-order pure theories. A model of Gödel–Bernays set theory GBC has the form
![]() ${\left \langle M,\in ^M,\mathcal {M}\right \rangle }$
, where the first-order part
${\left \langle M,\in ^M,\mathcal {M}\right \rangle }$
, where the first-order part
![]() ${\left \langle M,\in ^M\right \rangle }$
is a model of ZFC, and the second-order part
${\left \langle M,\in ^M\right \rangle }$
is a model of ZFC, and the second-order part
![]() $\mathcal {M}\subseteq P(M)$
is a collection of classes
$\mathcal {M}\subseteq P(M)$
is a collection of classes
![]() $X\subseteq M$
. The classes are allowed as atomic predicates into the first-order language, so that the model can assert
$X\subseteq M$
. The classes are allowed as atomic predicates into the first-order language, so that the model can assert
![]() $a\in X$
for the elements a of X in M, and we allow these class parameters into the ZFC collection and separation axiom schemes. The theory GBC also has the first-order class comprehension axiom, asserting that for any formula
$a\in X$
for the elements a of X in M, and we allow these class parameters into the ZFC collection and separation axiom schemes. The theory GBC also has the first-order class comprehension axiom, asserting that for any formula
![]() $\varphi $
involving only first-order quantifiers (over the sets) and class parameters
$\varphi $
involving only first-order quantifiers (over the sets) and class parameters
![]() $X_i$
, the collection
$X_i$
, the collection
![]() $X=\{{a\mid \varphi (a,X_0,\ldots ,X_n)}\}$
forms a class in
$X=\{{a\mid \varphi (a,X_0,\ldots ,X_n)}\}$
forms a class in
![]() $\mathcal {M}$
. The theory GBC also includes the axiom of global choice, which can be equivalently expressed either as the assertion that there is a global choice function F for which
$\mathcal {M}$
. The theory GBC also includes the axiom of global choice, which can be equivalently expressed either as the assertion that there is a global choice function F for which
![]() $F(u)\in u$
for every nonempty set u, as the assertion that there is a global well-order relation
$F(u)\in u$
for every nonempty set u, as the assertion that there is a global well-order relation
![]() $<$
on the universe of sets, a principle known also as the global well-order principle, or as the
$<$
on the universe of sets, a principle known also as the global well-order principle, or as the
![]() $\mathord {\mathrm {Ord}}$
enumeration principle, asserting specifically that there is such an order of type
$\mathord {\mathrm {Ord}}$
enumeration principle, asserting specifically that there is such an order of type
![]() $\mathord {\mathrm {Ord}}$
. Although these formulations of global choice are equivalent for the pure-set purposes of GBC, we warn the reader that they are no longer equivalent in the urelement class theories.
$\mathord {\mathrm {Ord}}$
. Although these formulations of global choice are equivalent for the pure-set purposes of GBC, we warn the reader that they are no longer equivalent in the urelement class theories.
The theory GBC is conservative over ZFC for assertions about sets, because we can equip any model
![]() $M\models \mathrm {ZFC}$
with all its first-order definable classes (with parameters), and this will satisfy all of GBC except possibly the global choice principle, since in some models there is no definable global well-order. But with the method of forcing we can add a generic global well-order to the universe, a forcing extension adding no sets, and then take the classes that are first-order definable using this new generic class parameter. The result is a model of GBC with the same sets as M, and so the conclusion is that any purely set-theoretic situation that can happen in ZFC can also happen in GBC, and this is an alternative equivalent way to express conservativity. It follows from the conservativity result that GBC is equiconsistent with ZFC. Despite what seems to be a very close semantic connection between GBC and ZFC, however, these theories (if consistent) are not mutually interpretable—the reason is that GBC is finitely axiomatizable and consequently cannot be interpreted in ZFC, for such an interpretation would make use of only finitely many axioms of ZFC, but ZFC proves the consistency of its finite fragments, and so such an interpretation of GBC in ZFC would violate the second incompleteness theorem.
$M\models \mathrm {ZFC}$
with all its first-order definable classes (with parameters), and this will satisfy all of GBC except possibly the global choice principle, since in some models there is no definable global well-order. But with the method of forcing we can add a generic global well-order to the universe, a forcing extension adding no sets, and then take the classes that are first-order definable using this new generic class parameter. The result is a model of GBC with the same sets as M, and so the conclusion is that any purely set-theoretic situation that can happen in ZFC can also happen in GBC, and this is an alternative equivalent way to express conservativity. It follows from the conservativity result that GBC is equiconsistent with ZFC. Despite what seems to be a very close semantic connection between GBC and ZFC, however, these theories (if consistent) are not mutually interpretable—the reason is that GBC is finitely axiomatizable and consequently cannot be interpreted in ZFC, for such an interpretation would make use of only finitely many axioms of ZFC, but ZFC proves the consistency of its finite fragments, and so such an interpretation of GBC in ZFC would violate the second incompleteness theorem.
Kelley–Morse set theory KM strengthens GBC with the second-order class comprehension axiom scheme, allowing one to define classes
![]() $\{{x\mid \varphi (x,Z)}\}$
by formulas
$\{{x\mid \varphi (x,Z)}\}$
by formulas
![]() $\varphi $
having second-order quantifiers ranging over the available classes of the model. This theory is not conservative over ZFC since it implies that there is a satisfaction class for first-order truth, and the existence of such a truth predicate implies
$\varphi $
having second-order quantifiers ranging over the available classes of the model. This theory is not conservative over ZFC since it implies that there is a satisfaction class for first-order truth, and the existence of such a truth predicate implies
![]() $\mathop {\mathrm {Con}}(\mathrm {ZFC})$
and
$\mathop {\mathrm {Con}}(\mathrm {ZFC})$
and
![]() $\mathop {\mathrm {Con}}(\mathrm {ZFC}+\mathop {\mathrm {Con}}(\mathrm {ZFC}))$
and much more (see [Reference Hamkins10] an elementary account). Meanwhile, if
$\mathop {\mathrm {Con}}(\mathrm {ZFC}+\mathop {\mathrm {Con}}(\mathrm {ZFC}))$
and much more (see [Reference Hamkins10] an elementary account). Meanwhile, if
![]() $\kappa $
is an inaccessible cardinal, then
$\kappa $
is an inaccessible cardinal, then
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of Kelley–Morse set theory, and so the consistency strength of KM is strictly between ZFC and ZFC plus an inaccessible cardinal. So KM ultimately is just a small step up in consistency strength from ZFC or GBC.
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of Kelley–Morse set theory, and so the consistency strength of KM is strictly between ZFC and ZFC plus an inaccessible cardinal. So KM ultimately is just a small step up in consistency strength from ZFC or GBC.
Gitman and Hamkins [Reference Gitman and Hamkins7] (see also [Reference Gitman, Hamkins, Caicedo, Cummings, Koellner and Larson6, Reference Gitman, Hamkins, Holy, Schlicht and Williams9]) have observed that even Kelley–Morse set theory KM does not prove the class choice principle CC, which asserts that for every class I, if for every individual
![]() $i\in I$
there is a class X for which
$i\in I$
there is a class X for which
![]() $\varphi (i,X,I)$
, then there is a class
$\varphi (i,X,I)$
, then there is a class
![]() $X\subseteq I\times V$
such that for every
$X\subseteq I\times V$
such that for every
![]() $i\in I$
we have
$i\in I$
we have
![]() $\varphi (i,X_i,I)$
, where
$\varphi (i,X_i,I)$
, where
![]() $X_i=\{{x\mid (i,x)\in X}\}$
is the ith section of the class X. For example, if for every n there is a class X with
$X_i=\{{x\mid (i,x)\in X}\}$
is the ith section of the class X. For example, if for every n there is a class X with
![]() $\varphi (n,X)$
, then CC allows you to put such classes together into a single class
$\varphi (n,X)$
, then CC allows you to put such classes together into a single class
![]() $X\subseteq \omega \times V$
such that
$X\subseteq \omega \times V$
such that
![]() $\varphi (n,X_n)$
for all n. This is essentially a choice principle or collection principle for classes, and even the
$\varphi (n,X_n)$
for all n. This is essentially a choice principle or collection principle for classes, and even the
![]() $\omega $
-indexed version
$\omega $
-indexed version
![]() $\omega $
-CC is not provable in KM.
$\omega $
-CC is not provable in KM.
Nevertheless, every model of KM admits a submodel with the same sets (but possibly fewer classes), which is a model of KM+CC (see [Reference Gitman and Hamkins7]). It follows that KM and KM+CC are mutually interpretable theories and consequently also equiconsistent. But they are not bi-interpretable, in light of [Reference Enayat, van Eijck, Iemhoff and Joosten4, Reference Freire and Hamkins5]. Meanwhile, the class choice principle supports important applications of Kelley–Morse set theory, and KM+CC should be seen as a natural, robust extension of KM.
4.1 Interpretation of Kelley–Morse in a first-order set theory
The class choice principle supports an important bi-interpretation phenomenon of Kelley–Morse set theory, showing that KM+CC is bi-interpretable with first-order strengthenings of
![]() $\mathrm {ZFC}^-$
with an inaccessible cardinal. The observation is due originally to Marek and Mostowski [Reference Marek, Mostowski, Müller, Oberschelp and Potthoff17], with perhaps an earlier form in [Reference Scott22]. But see also the excellently thorough presentation of Williams [Reference Williams24].
$\mathrm {ZFC}^-$
with an inaccessible cardinal. The observation is due originally to Marek and Mostowski [Reference Marek, Mostowski, Müller, Oberschelp and Potthoff17], with perhaps an earlier form in [Reference Scott22]. But see also the excellently thorough presentation of Williams [Reference Williams24].
Theorem 4.1 (Marek, Mostowski)
The following theories are bi-interpretable:
-
(1) Kelley–Morse set theory KM with the class choice principle CC,
-
(2)
 $\mathrm {ZFC}^-+$
there is a largest cardinal, which is inaccessible.
$\mathrm {ZFC}^-+$
there is a largest cardinal, which is inaccessible.
Proof To interpret the first theory in the second, assume a set-theoretic universe
![]() ${\left \langle M,\in ^M\right \rangle }$
satisfies
${\left \langle M,\in ^M\right \rangle }$
satisfies
![]() $\mathrm {ZFC}^-$
and has a largest cardinal
$\mathrm {ZFC}^-$
and has a largest cardinal
![]() $\kappa $
, which is inaccessible there. It follows that
$\kappa $
, which is inaccessible there. It follows that
![]() $M_{\kappa }=(V_{\kappa })^M$
is a model of ZFC. Inside M, we can consider the sets available that would form classes on
$M_{\kappa }=(V_{\kappa })^M$
is a model of ZFC. Inside M, we can consider the sets available that would form classes on
![]() $M_{\kappa }$
, that is, the set
$M_{\kappa }$
, that is, the set
![]() $\mathcal {M}=\{{X\in M\mid M\models X\subseteq M_{\kappa }}\}$
. The point now is that
$\mathcal {M}=\{{X\in M\mid M\models X\subseteq M_{\kappa }}\}$
. The point now is that
![]() ${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
is a model of Kelley–Morse set theory by the same reasoning as in ZFC that
${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
is a model of Kelley–Morse set theory by the same reasoning as in ZFC that
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of KM whenever
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of KM whenever
![]() $\kappa $
is inaccessible—everything works fine just in
$\kappa $
is inaccessible—everything works fine just in
![]() $\mathrm {ZFC}^-$
. Note that the power set axiom holds below
$\mathrm {ZFC}^-$
. Note that the power set axiom holds below
![]() $\kappa $
in M as a consequence of what it means for
$\kappa $
in M as a consequence of what it means for
![]() $\kappa $
to be inaccessible; and we get the class choice principle CC in this KM model, since instances of class choice in
$\kappa $
to be inaccessible; and we get the class choice principle CC in this KM model, since instances of class choice in
![]() ${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
amount to instances of the first-order collection axiom in M, which holds because collection is part of
${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
amount to instances of the first-order collection axiom in M, which holds because collection is part of
![]() $\mathrm {ZFC}^-$
.
$\mathrm {ZFC}^-$
.
For the converse interpretation, we provide the construction and sketch the argument, but refer the reader to [Reference Williams24] for fuller details. We begin with a model
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of KM+CC and shall interpret a corresponding model
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of KM+CC and shall interpret a corresponding model
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
of
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
of
![]() $\mathrm {ZFC}^-$
with a largest cardinal
$\mathrm {ZFC}^-$
with a largest cardinal
![]() $\kappa $
, which is inaccessible there. We employ a standard technique of coding sets with binary relations, perhaps used more commonly when coding hereditarily countable sets with relations on
$\kappa $
, which is inaccessible there. We employ a standard technique of coding sets with binary relations, perhaps used more commonly when coding hereditarily countable sets with relations on
![]() ${\mathbb N}$
, but the same idea works higher up, even with proper class codes as here, resulting in the unrolling of a model of second-order set theory to a model of first-order set theory with sets of higher rank. Specifically, following [Reference Williams24], let us say that a membership code is an extensional class directed graph relation E with a unique maximal node. (Let us agree to consider the empty relation always with
${\mathbb N}$
, but the same idea works higher up, even with proper class codes as here, resulting in the unrolling of a model of second-order set theory to a model of first-order set theory with sets of higher rank. Specifically, following [Reference Williams24], let us say that a membership code is an extensional class directed graph relation E with a unique maximal node. (Let us agree to consider the empty relation always with
![]() $\varnothing $
as the unique maximal node, so the domain of individuals for any relation E will be determined by E.)
$\varnothing $
as the unique maximal node, so the domain of individuals for any relation E will be determined by E.)
As an example, for any set x consider the membership relation
![]() ${\left \langle \mathop {\mathrm {TC}}(\{{x}\}),\in \right \rangle }$
on the transitive closure of the singleton
${\left \langle \mathop {\mathrm {TC}}(\{{x}\}),\in \right \rangle }$
on the transitive closure of the singleton
![]() $\{{x}\}$
. This is an extensional directed graph having a unique maximal node, which is x itself—the lower nodes represent the elements of x and the elements of elements and so forth. Indeed, this is the principal motivating example of membership codes, for we shall think of the membership codes as representing sets completely in analogy with this case. Thus, we say that two codes are equivalent
$\{{x}\}$
. This is an extensional directed graph having a unique maximal node, which is x itself—the lower nodes represent the elements of x and the elements of elements and so forth. Indeed, this is the principal motivating example of membership codes, for we shall think of the membership codes as representing sets completely in analogy with this case. Thus, we say that two codes are equivalent
![]() $E\sim F$
, if they are isomorphic as directed graphs. For any node y in the field of the relation E, let
$E\sim F$
, if they are isomorphic as directed graphs. For any node y in the field of the relation E, let
![]() $E\downarrow y$
be the graph obtained by restricting to y and nodes that are hereditarily below y—this also is a membership code, and we define
$E\downarrow y$
be the graph obtained by restricting to y and nodes that are hereditarily below y—this also is a membership code, and we define
![]() $F\mathrel {\varepsilon } E$
if and only if
$F\mathrel {\varepsilon } E$
if and only if
![]() $F\sim E\downarrow y$
for some y with
$F\sim E\downarrow y$
for some y with
![]() $y\mathrel {E} x$
, where x is the maximal node of E.
$y\mathrel {E} x$
, where x is the maximal node of E.
Williams [Reference Williams24] proves various welcome properties about these codes from weak fragments of KM. For example, in
![]() $\text {GBc}^-$
one can prove that the isomorphisms of membership codes are unique when they exist, and initial partial isomorphisms of codes agree on their common domain. With ETR, one can thus prove that any two codes admit a maximal partial initial isomorphism, and using this, one can prove extensionality for the codes.
$\text {GBc}^-$
one can prove that the isomorphisms of membership codes are unique when they exist, and initial partial isomorphisms of codes agree on their common domain. With ETR, one can thus prove that any two codes admit a maximal partial initial isomorphism, and using this, one can prove extensionality for the codes.
Indeed, let
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
be the structure arising from the corresponding equivalence classes
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
be the structure arising from the corresponding equivalence classes
![]() $[E]_{\sim }$
considered under the
$[E]_{\sim }$
considered under the
![]() $\mathrel {\varepsilon }$
membership relation. This model is interpretable in
$\mathrel {\varepsilon }$
membership relation. This model is interpretable in
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, and the main observation to make is that it satisfies
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, and the main observation to make is that it satisfies
![]() $\mathrm {ZFC}^-$
with a largest cardinal, which is inaccessible there. We refer the reader to [Reference Williams24] for the details. The class choice principle CC is used in order to verify the collection axiom in W, since collecting sets in W amounts to collecting classes together in
$\mathrm {ZFC}^-$
with a largest cardinal, which is inaccessible there. We refer the reader to [Reference Williams24] for the details. The class choice principle CC is used in order to verify the collection axiom in W, since collecting sets in W amounts to collecting classes together in
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, and this is exactly what CC enables. The largest cardinal
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, and this is exactly what CC enables. The largest cardinal
![]() $\kappa $
is simply
$\kappa $
is simply
![]() $\mathord {\mathrm {Ord}}^V$
, which is easily coded in
$\mathord {\mathrm {Ord}}^V$
, which is easily coded in
![]() $\mathcal {V}$
and is inaccessible there because
$\mathcal {V}$
and is inaccessible there because
![]() $\mathord {\mathrm {Ord}}$
is closed under power sets and is regular with respect to classes in
$\mathord {\mathrm {Ord}}$
is closed under power sets and is regular with respect to classes in
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
Finally, we observe that these interpretations provide a bi-interpretation. The original
![]() $\mathrm {ZFC}^-$
model
$\mathrm {ZFC}^-$
model
![]() ${\left \langle M,\in ^M\right \rangle }$
with a largest cardinal
${\left \langle M,\in ^M\right \rangle }$
with a largest cardinal
![]() $\kappa $
, which is inaccessible, can see how it is copied into
$\kappa $
, which is inaccessible, can see how it is copied into
![]() ${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
, since it can form the membership codes
${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
, since it can form the membership codes
![]() ${\left \langle \mathop {\mathrm {TC}}(\{{x}\}),\in ^M\right \rangle }$
for any set x, and these will have size
${\left \langle \mathop {\mathrm {TC}}(\{{x}\}),\in ^M\right \rangle }$
for any set x, and these will have size
![]() $\kappa $
and thus have isomorphic copies appearing in
$\kappa $
and thus have isomorphic copies appearing in
![]() $\mathcal {M}$
. And so the model W interpreted inside
$\mathcal {M}$
. And so the model W interpreted inside
![]() ${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
will be a copy of
${\left \langle M_{\kappa },\in ^M,\mathcal {M}\right \rangle }$
will be a copy of
![]() ${\left \langle M,\in ^M\right \rangle }$
. And the model
${\left \langle M,\in ^M\right \rangle }$
. And the model
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of KM+CC can see how it arises as
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of KM+CC can see how it arises as
![]() $W_{\kappa }$
inside the interpreted model
$W_{\kappa }$
inside the interpreted model
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
. So this is a bi-interpretation.
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
. So this is a bi-interpretation.
Since KM is mutually interpretable (although not bi-interpretable) with
![]() $\mathrm {KM}+\mathrm {CC}$
, it follows that KM is mutually interpretable with
$\mathrm {KM}+\mathrm {CC}$
, it follows that KM is mutually interpretable with
![]() $\mathrm {ZFC}^-$
plus the assertion that there is a largest which is inaccessible.
$\mathrm {ZFC}^-$
plus the assertion that there is a largest which is inaccessible.
5 Class theory with urelements
Let us now introduce the urelement analogues of GBC and KM. Namely, GBCU is the two-sorted theory for models of the form
![]() ${\left \langle M,\in ^M,{\mathbb A},\mathcal {M}\right \rangle }$
, where
${\left \langle M,\in ^M,{\mathbb A},\mathcal {M}\right \rangle }$
, where
![]() ${\left \langle M,\in ^M,{\mathbb A}\right \rangle }$
is a model of ZFCU, allowing class parameters in the collection and separation schemes, and
${\left \langle M,\in ^M,{\mathbb A}\right \rangle }$
is a model of ZFCU, allowing class parameters in the collection and separation schemes, and
![]() $\mathcal {M}$
is a collection of classes in M that fulfills the first-order class comprehension axiom (in the language with
$\mathcal {M}$
is a collection of classes in M that fulfills the first-order class comprehension axiom (in the language with
![]() $\in $
and
$\in $
and
![]() ${\mathbb A}$
, allowing class parameters), plus the assertion that there is a global well-order
${\mathbb A}$
, allowing class parameters), plus the assertion that there is a global well-order
![]() $<$
of the universe. The global well-order
$<$
of the universe. The global well-order
![]() $<$
is simply one of the classes in
$<$
is simply one of the classes in
![]() $\mathcal {M}$
, as is the class of all urelements. The theory KMU extends GBCU with the second-order class comprehension axiom. The theories
$\mathcal {M}$
, as is the class of all urelements. The theory KMU extends GBCU with the second-order class comprehension axiom. The theories
![]() $\mathrm {KMU}$
and
$\mathrm {KMU}$
and
![]() $\mathrm {GBCU}$
are formulated analogously with the enumeration predicate
$\mathrm {GBCU}$
are formulated analogously with the enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
for the atoms rather than merely the predicate
$\smash {\vec {{\mathbb A}}}$
for the atoms rather than merely the predicate
![]() ${\mathbb A}$
. We warn the reader that the various formulations of global choice, although equivalent in pure set theory, come apart in the urelement context (see [Reference Howard, Rubin and Rubin13]). In particular, we won’t generally be able to convert every class well-order of the universe to a well-order of type
${\mathbb A}$
. We warn the reader that the various formulations of global choice, although equivalent in pure set theory, come apart in the urelement context (see [Reference Howard, Rubin and Rubin13]). In particular, we won’t generally be able to convert every class well-order of the universe to a well-order of type
![]() $\mathord {\mathrm {Ord}}$
, since there may simply be too many urelements for this to be possible. We shall discuss this issue in further depth later.
$\mathord {\mathrm {Ord}}$
, since there may simply be too many urelements for this to be possible. We shall discuss this issue in further depth later.
In any model of Gödel–Bernays set theory
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, with any class
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
, with any class
![]() $A\in \mathcal {V}$
, we can define the interpreted urelement model
$A\in \mathcal {V}$
, we can define the interpreted urelement model
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
in analogy with the first-order case, defining
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
in analogy with the first-order case, defining
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
,
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
,
![]() $\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
and
$\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}$
and
![]() $\smash {\vec {{\mathbb A}}}$
just as we did for the ZFC context in Section 2, but now also interpreting the second-order part of the models by placing the classes
$\smash {\vec {{\mathbb A}}}$
just as we did for the ZFC context in Section 2, but now also interpreting the second-order part of the models by placing the classes
![]() $\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}=\{{B\in \mathcal {V}\mid B\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}}\}$
. That is, the new classes are simply the old classes that happen to be subclasses of
$\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}=\{{B\in \mathcal {V}\mid B\subseteq V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}}\}$
. That is, the new classes are simply the old classes that happen to be subclasses of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
.
Theorem 5.1. Every model
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of GBC is bi-interpretable, for every class
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of GBC is bi-interpretable, for every class
![]() $A\in \mathcal {V}$
, with the interpreted model
$A\in \mathcal {V}$
, with the interpreted model
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
, which is a model of
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
, which is a model of
![]() $\mathrm {GBCU} +$
“there are A many urelements.” If the original model satisfies KM, then the interpreted model satisfies
$\mathrm {GBCU} +$
“there are A many urelements.” If the original model satisfies KM, then the interpreted model satisfies
![]() $\mathrm {KMU}$
, and if the original model satisfies the class choice principle CC, then so does the interpreted model.
$\mathrm {KMU}$
, and if the original model satisfies the class choice principle CC, then so does the interpreted model.
Proof We know that
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
satisfies
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
satisfies
![]() $\mathrm {ZFCU}+$
“there are A many urelements,” and we can allow class parameters into the collection and separation schemes. And since
$\mathrm {ZFCU}+$
“there are A many urelements,” and we can allow class parameters into the collection and separation schemes. And since
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is first-order definable in the original model, any first-order definable class in
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
is first-order definable in the original model, any first-order definable class in
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
is also definable in the original model, and so it exists as a class in
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}}\right \rangle }$
is also definable in the original model, and so it exists as a class in
![]() $\mathcal {V}$
and will consequently be added to
$\mathcal {V}$
and will consequently be added to
![]() $\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. If the original model satisfies KM, then this argument works also with second-order definable classes, and if class choice CC holds originally, it will hold in the interpreted model, since instances of class choice there amount to instances of class choice in the original model. Since V can see how it is interpreted into the pure sets of
$\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. If the original model satisfies KM, then this argument works also with second-order definable classes, and if class choice CC holds originally, it will hold in the interpreted model, since instances of class choice there amount to instances of class choice in the original model. Since V can see how it is interpreted into the pure sets of
![]() $V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
via
$V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
via
![]() $u\mapsto \check u$
, it can also transfer all the classes of
$u\mapsto \check u$
, it can also transfer all the classes of
![]() $\mathcal {V}$
into the corresponding classes of pure sets
$\mathcal {V}$
into the corresponding classes of pure sets
![]() $X\mapsto \hat X=\{{\check u\mid u\in X}\}$
, and thus
$X\mapsto \hat X=\{{\check u\mid u\in X}\}$
, and thus
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
can see how it is copied into
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
can see how it is copied into
![]() ${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
. Conversely, the latter model can use the urelement enumeration predicate
${\left \langle V{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }},\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\smash {\vec {{\mathbb A}}},\mathcal {V}{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}\right \rangle }$
. Conversely, the latter model can use the urelement enumeration predicate
![]() $\smash {\vec {{\mathbb A}}}$
to see how it arises from the pure sets by the construction we have specified. So this is a bi-interpretation.
$\smash {\vec {{\mathbb A}}}$
to see how it arises from the pure sets by the construction we have specified. So this is a bi-interpretation.
The following theories are consequently all bi-interpretable with parameters:
-
(1) GBC,
-
(2)
 $\mathrm {GBCU}+$
“there are
$\mathrm {GBCU}+$
“there are
 $\omega $
many atoms,”
$\omega $
many atoms,” -
(3)
 $\mathrm {GBCU}+$
“there are
$\mathrm {GBCU}+$
“there are
 $\mathord {\mathrm {Ord}}$
many atoms,”
$\mathord {\mathrm {Ord}}$
many atoms,” -
(4)
 $\mathrm {GBCU}+$
“there are V many atoms,”
$\mathrm {GBCU}+$
“there are V many atoms,”
as well as the following theories:
-
(1) KM,
-
(2)
 $\mathrm {KMU}+$
“there are
$\mathrm {KMU}+$
“there are
 $\omega $
many atoms,”
$\omega $
many atoms,” -
(3)
 $\mathrm {KMU}+$
“there are
$\mathrm {KMU}+$
“there are
 $\mathord {\mathrm {Ord}}$
many atoms,”
$\mathord {\mathrm {Ord}}$
many atoms,” -
(4)
 $\mathrm {KMU}+$
“there are V many atoms,”
$\mathrm {KMU}+$
“there are V many atoms,”
and the following:
-
(1) KM + CC,
-
(2)
 $\mathrm {KMU}+\mathrm {CC}+$
“there are
$\mathrm {KMU}+\mathrm {CC}+$
“there are
 $\omega $
many atoms,”
$\omega $
many atoms,” -
(3)
 $\mathrm {KMU}+\mathrm {CC}+$
“there are
$\mathrm {KMU}+\mathrm {CC}+$
“there are
 $\mathord {\mathrm {Ord}}$
many atoms,”
$\mathord {\mathrm {Ord}}$
many atoms,” -
(4)
 $\mathrm {KMU}+\mathrm {CC}+$
“there are V many atoms,”
$\mathrm {KMU}+\mathrm {CC}+$
“there are V many atoms,” -
(5)
 $\mathrm {ZFC}^-+$
“there is a largest cardinal
$\mathrm {ZFC}^-+$
“there is a largest cardinal
 $\kappa $
, which is inaccessible,”
$\kappa $
, which is inaccessible,” -
(6)
 $\mathrm {ZFCU}^{-}+$
“there is a largest cardinal
$\mathrm {ZFCU}^{-}+$
“there is a largest cardinal
 $\kappa $
, which is inaccessible, and
$\kappa $
, which is inaccessible, and
 $\kappa $
many atoms.”
$\kappa $
many atoms.”
Note that we can take a class parameter enumerating all the urelements, if desired. In the next section we shall explain how to achieve more than
![]() $\mathord {\mathrm {Ord}}$
many urelements in models of GBCU and KMU.
$\mathord {\mathrm {Ord}}$
many urelements in models of GBCU and KMU.
6 Abundant atoms
In urelement set theory, for any cardinal
![]() $\kappa $
we define the corresponding hereditary class
$\kappa $
we define the corresponding hereditary class
![]() $H_{\kappa }(A)$
to be
$H_{\kappa }(A)$
to be
![]() $(H_{\kappa })^{V(A)}$
, that is, the class of atoms and sets in
$(H_{\kappa })^{V(A)}$
, that is, the class of atoms and sets in
![]() $V(A)$
of hereditary size less than
$V(A)$
of hereditary size less than
![]() $\kappa $
, the sets whose transitive closure has size less than
$\kappa $
, the sets whose transitive closure has size less than
![]() $\kappa $
. If we are working in a second-order urelement theory in the ambient universe
$\kappa $
. If we are working in a second-order urelement theory in the ambient universe
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, then we may equip
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, then we may equip
![]() $H_{\kappa }(A)$
with the family of classes
$H_{\kappa }(A)$
with the family of classes
![]() $\mathcal {H}=\mathcal {V}\upharpoonright H_{\kappa }(A)$
, consisting of all the classes
$\mathcal {H}=\mathcal {V}\upharpoonright H_{\kappa }(A)$
, consisting of all the classes
![]() $X\in \mathcal {V}$
for which
$X\in \mathcal {V}$
for which
![]() $X\subseteq H_{\kappa }(A)$
. Since every atom
$X\subseteq H_{\kappa }(A)$
. Since every atom
![]() $a\in A$
appears in
$a\in A$
appears in
![]() $H_{\kappa }(A)$
, it follows that
$H_{\kappa }(A)$
, it follows that
![]() $A\subseteq H_{\kappa }(A)$
and consequently also every class of urelements
$A\subseteq H_{\kappa }(A)$
and consequently also every class of urelements
![]() $B\subseteq A$
is a class in the hereditary model
$B\subseteq A$
is a class in the hereditary model
![]() $\mathcal {H}$
. Thus, although
$\mathcal {H}$
. Thus, although
![]() $H_{\kappa }(A)$
has many fewer sets than
$H_{\kappa }(A)$
has many fewer sets than
![]() $V(A)$
, we nevertheless retain exactly the same classes of urelements in
$V(A)$
, we nevertheless retain exactly the same classes of urelements in
![]() $\mathcal {H}$
as in
$\mathcal {H}$
as in
![]() $\mathcal {V}$
.
$\mathcal {V}$
.

Theorem 6.1. Assume that GBCU holds in
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
with urelements A, and suppose
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
with urelements A, and suppose
![]() $\kappa $
is an inaccessible cardinal in this model. Then
$\kappa $
is an inaccessible cardinal in this model. Then
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of GBCU. If the ambient universe satisfies KMU, then this hereditary model also satisfies KMU, and similarly if CC holds initially, then it holds in the hereditary model.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of GBCU. If the ambient universe satisfies KMU, then this hereditary model also satisfies KMU, and similarly if CC holds initially, then it holds in the hereditary model.
Proof Consider the structure
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
as a model of second-order urelement set theory. What we claim is that this is a model of GBCU. Using the fact that
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
as a model of second-order urelement set theory. What we claim is that this is a model of GBCU. Using the fact that
![]() $\kappa $
is inaccessible, it is straightforward to verify that
$\kappa $
is inaccessible, it is straightforward to verify that
![]() ${\left \langle H_{\kappa }(A),\in \right \rangle }$
is a model of ZFCU, even with class parameters from
${\left \langle H_{\kappa }(A),\in \right \rangle }$
is a model of ZFCU, even with class parameters from
![]() $\mathcal {H}$
, using that this is a transitive class closed under pairing, union, and power sets, and contains as an element every subset of it of size less than
$\mathcal {H}$
, using that this is a transitive class closed under pairing, union, and power sets, and contains as an element every subset of it of size less than
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $H_{\kappa }(A)$
is a definable class in the ambient universe, it follows that any first-order definable class
$H_{\kappa }(A)$
is a definable class in the ambient universe, it follows that any first-order definable class
![]() $X\subseteq H_{\kappa }(A)$
, allowing class parameters, will exist in
$X\subseteq H_{\kappa }(A)$
, allowing class parameters, will exist in
![]() $\mathcal {V}$
and hence be placed into
$\mathcal {V}$
and hence be placed into
![]() $\mathcal {H}$
. So
$\mathcal {H}$
. So
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will fulfill first-order class comprehension. It will satisfy the global well-order principle, since
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will fulfill first-order class comprehension. It will satisfy the global well-order principle, since
![]() $H_{\kappa }(A)$
admits a well-order in the ambient universe and this class will therefore exist in
$H_{\kappa }(A)$
admits a well-order in the ambient universe and this class will therefore exist in
![]() $\mathcal {H}$
. So
$\mathcal {H}$
. So
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of GBCU.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of GBCU.
Furthermore, if the ambient universe
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
satisfies KMU, then classes defined by second-order definitions also will exist and hence be in
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
satisfies KMU, then classes defined by second-order definitions also will exist and hence be in
![]() $\mathcal {H}$
, and so
$\mathcal {H}$
, and so
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of KMU. And instances of CC in
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of KMU. And instances of CC in
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
similarly reduce to instances of CC in the ambient universe.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
similarly reduce to instances of CC in the ambient universe.
Let us look a little more closely at this model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, for there are some interesting things to notice. The ordinals of
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, for there are some interesting things to notice. The ordinals of
![]() $H_{\kappa }(A)$
are exactly the ordinals below
$H_{\kappa }(A)$
are exactly the ordinals below
![]() $\kappa $
, and so if A is larger than
$\kappa $
, and so if A is larger than
![]() $\kappa $
in the original universe, then because it contains every urelement in A, the class
$\kappa $
in the original universe, then because it contains every urelement in A, the class
![]() $H_{\kappa }(A)$
will not be equinumerous with
$H_{\kappa }(A)$
will not be equinumerous with
![]() $\kappa $
. In other words,
$\kappa $
. In other words,
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of GBCU or KMU in which every class has a well-order, but the universe has no
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
will be a model of GBCU or KMU in which every class has a well-order, but the universe has no
![]() $\mathord {\mathrm {Ord}}$
-enumeration. In particular, the so-called limitation of size principle fails in this model, even though the global choice and global well-order principles hold.
$\mathord {\mathrm {Ord}}$
-enumeration. In particular, the so-called limitation of size principle fails in this model, even though the global choice and global well-order principles hold.
Let us now assume specifically that A is equinumerous with
![]() $\mathord {\mathrm {Ord}}$
in the original model and look a little more closely at what kinds of classes there are in
$\mathord {\mathrm {Ord}}$
in the original model and look a little more closely at what kinds of classes there are in
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
. Since A has size
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
. Since A has size
![]() $\mathord {\mathrm {Ord}}$
in the original universe
$\mathord {\mathrm {Ord}}$
in the original universe
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, it follows that for every cardinal
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, it follows that for every cardinal
![]() $\delta $
, including cardinals
$\delta $
, including cardinals
![]() $\delta \geq \kappa $
, there will be a class
$\delta \geq \kappa $
, there will be a class
![]() $B\subseteq A$
of size
$B\subseteq A$
of size
![]() $\delta $
in
$\delta $
in
![]() $V(A)$
. Such a class will have been a set in
$V(A)$
. Such a class will have been a set in
![]() $V(A)$
, but is a proper class of urelements in
$V(A)$
, but is a proper class of urelements in
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, although it is smaller than A in size, in the sense that these two proper classes are not equinumerous.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, although it is smaller than A in size, in the sense that these two proper classes are not equinumerous.
In this model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, let us say that a class is small, if it is strictly smaller in equinumerosity than the class A of all urelements. There are many small classes in this model, since all the cardinals between
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, let us say that a class is small, if it is strictly smaller in equinumerosity than the class A of all urelements. There are many small classes in this model, since all the cardinals between
![]() $\kappa $
and
$\kappa $
and
![]() $\mathord {\mathrm {Ord}}$
in the original universe
$\mathord {\mathrm {Ord}}$
in the original universe
![]() $V(A)$
are realized by small proper classes
$V(A)$
are realized by small proper classes
![]() $B\subseteq A$
in
$B\subseteq A$
in
![]() $\mathcal {H}$
. Indeed, the small classes
$\mathcal {H}$
. Indeed, the small classes
![]() $B\subseteq A$
are exactly the classes
$B\subseteq A$
are exactly the classes
![]() $B\subseteq A$
that are sets in
$B\subseteq A$
that are sets in
![]() $V(A)$
. It follows from this that if
$V(A)$
. It follows from this that if
![]() $B\subseteq A$
is a small class of urelements, then it has a power set in
$B\subseteq A$
is a small class of urelements, then it has a power set in
![]() $V(A)$
, and so we may find a class
$V(A)$
, and so we may find a class
![]() $D\subseteq I\times B$
, for some small class I, such that the sections
$D\subseteq I\times B$
, for some small class I, such that the sections
![]() $D_i=\{{b\in B\mid (i,b)\in D}\}$
are all different and every class
$D_i=\{{b\in B\mid (i,b)\in D}\}$
are all different and every class
![]() $B'\subseteq B$
is realized as
$B'\subseteq B$
is realized as
![]() $D_i$
for some
$D_i$
for some
![]() $i\in I$
. In other words, the model
$i\in I$
. In other words, the model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
can see that every small class of urelements has a small power class, indexed by a class D upon a small class I in that way. It also follows that for every small class I and every class
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
can see that every small class of urelements has a small power class, indexed by a class D upon a small class I in that way. It also follows that for every small class I and every class
![]() $D\subseteq I\times A$
, such that
$D\subseteq I\times A$
, such that
![]() $D_i$
is small for every
$D_i$
is small for every
![]() $i\in I$
, then D itself is small. This is simply because the union of set many sets in
$i\in I$
, then D itself is small. This is simply because the union of set many sets in
![]() $V(A)$
is a set, by the replacement axiom. This fact also is visible in
$V(A)$
is a set, by the replacement axiom. This fact also is visible in
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
.
Let us give a name to these properties.
Definition 6.2. The abundant atom axiom (AAA) is the assertion in urelement class theory that:
-
(1) The class of urelements is strictly larger than
 $\mathord {\mathrm {Ord}}$
.
$\mathord {\mathrm {Ord}}$
. -
(2) Every small class of urelements admits a small power class, that is, for every small class B there is a small class I and
 $D\subseteq I\times B$
such that every subclass of B is realized as a section
$D\subseteq I\times B$
such that every subclass of B is realized as a section
 $D_i$
.
$D_i$
. -
(3) Every small-indexed class of small classes is small, that is, if I is a small class and every section
 $D_i$
of a class
$D_i$
of a class
 $D\subseteq I\times A$
is small, then D itself is small.
$D\subseteq I\times A$
is small, then D itself is small.
And so we established the following improvement on Theorem 6.1.
Theorem 6.3. Assume that GBCU holds with
![]() $\mathord {\mathrm {Ord}}$
many urelements A and
$\mathord {\mathrm {Ord}}$
many urelements A and
![]() $\kappa $
is an inaccessible cardinal. Then
$\kappa $
is an inaccessible cardinal. Then
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of GBCU plus the abundant atom axiom AAA. If the ambient universe satisfies KMU, then this hereditary model also satisfies KMU. If CC holds originally, then it holds in the hereditary model.
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of GBCU plus the abundant atom axiom AAA. If the ambient universe satisfies KMU, then this hereditary model also satisfies KMU. If CC holds originally, then it holds in the hereditary model.
Let us deepen the analysis by revealing the bi-interpretation phenomenon at the heart of the situation.
Theorem 6.4. The following theories are bi-interpretable, with parameters.
-
(1)
 $\mathrm {KMU}+\mathrm {CC}+{}$
the abundant atom axiom.
$\mathrm {KMU}+\mathrm {CC}+{}$
the abundant atom axiom. -
(2)
 $\mathrm {KM}+\mathrm {CC}+{}$
there is an inaccessible cardinal.
$\mathrm {KM}+\mathrm {CC}+{}$
there is an inaccessible cardinal. -
(3)
 $\mathrm {KMU}+\mathrm {CC}+{}$
there is an inaccessible cardinal and
$\mathrm {KMU}+\mathrm {CC}+{}$
there is an inaccessible cardinal and
 $\mathord {\mathrm {Ord}}$
many atoms.
$\mathord {\mathrm {Ord}}$
many atoms. -
(4)
 $\mathrm {ZFC}^-+{}$
there are two inaccessible cardinals
$\mathrm {ZFC}^-+{}$
there are two inaccessible cardinals
 $\kappa <\lambda $
, and
$\kappa <\lambda $
, and
 $\lambda $
is the largest cardinal.
$\lambda $
is the largest cardinal. -
(5)
 $\mathrm {ZFCU}^{-}+{}$
there are two inaccessible cardinals
$\mathrm {ZFCU}^{-}+{}$
there are two inaccessible cardinals
 $\kappa <\lambda $
, where
$\kappa <\lambda $
, where
 $\lambda $
is the largest cardinal, and there are
$\lambda $
is the largest cardinal, and there are
 $\lambda $
many atoms.
$\lambda $
many atoms.
Proof The relationships of the five bi-interpretable models are illustrated in Figure 1, but note that the model V at lower left is not itself used directly in the interpretations. Let us start by interpreting from the bottom right of the figure to the top left, interpreting from theory (1) to theory (4). Suppose
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
satisfies
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
satisfies
![]() $\mathrm {KMU}+\mathrm {CC}$
with the abundant atom axiom. We may follow the unrolling construction of Theorem 4.1, which actually works equally well in
$\mathrm {KMU}+\mathrm {CC}$
with the abundant atom axiom. We may follow the unrolling construction of Theorem 4.1, which actually works equally well in
![]() $\mathrm {KMU}+\mathrm {CC}$
as in
$\mathrm {KMU}+\mathrm {CC}$
as in
![]() $\mathrm {KM}+\mathrm {CC}$
. That is, we consider the class membership codes E, allowing class relations not just on
$\mathrm {KM}+\mathrm {CC}$
. That is, we consider the class membership codes E, allowing class relations not just on
![]() $\mathord {\mathrm {Ord}}$
or on the pure sets V, but on the class of urelements, and define equivalence
$\mathord {\mathrm {Ord}}$
or on the pure sets V, but on the class of urelements, and define equivalence
![]() $E\sim F$
and membership
$E\sim F$
and membership
![]() $E\mathrel {\varepsilon } F$
. The arguments of Theorem 4.1 show that the resulting universe
$E\mathrel {\varepsilon } F$
. The arguments of Theorem 4.1 show that the resulting universe
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is a model of
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is a model of
![]() $\mathrm {ZFC}^-$
. The ordinals of V become an inaccessible cardinal
$\mathrm {ZFC}^-$
. The ordinals of V become an inaccessible cardinal
![]() $\kappa $
in W. Because of the abundant atom axiom, however, there will be cardinals in W larger than
$\kappa $
in W. Because of the abundant atom axiom, however, there will be cardinals in W larger than
![]() $\kappa $
. The shortest well-ordering of the class of atoms will become an inaccessible cardinal
$\kappa $
. The shortest well-ordering of the class of atoms will become an inaccessible cardinal
![]() $\lambda $
of W strictly above
$\lambda $
of W strictly above
![]() $\kappa $
. The cardinals below
$\kappa $
. The cardinals below
![]() $\lambda $
in W are precisely those with class membership codes that are small in
$\lambda $
in W are precisely those with class membership codes that are small in
![]() $\mathcal {V}$
. The abundant atom axiom ensures
$\mathcal {V}$
. The abundant atom axiom ensures
![]() $\lambda $
is inaccessible in W, namely, a strong limit because any small class membership code will have a small class code for the power set and regular, because any small class code for a set of cardinals less than
$\lambda $
is inaccessible in W, namely, a strong limit because any small class membership code will have a small class code for the power set and regular, because any small class code for a set of cardinals less than
![]() $\lambda $
will also be less than
$\lambda $
will also be less than
![]() $\lambda $
. Thus, W is a model of
$\lambda $
. Thus, W is a model of
![]() $\mathrm {ZFC}^-$
with two
$\mathrm {ZFC}^-$
with two
![]() $\kappa <\lambda $
, where
$\kappa <\lambda $
, where
![]() $\lambda $
is the largest cardinal.
$\lambda $
is the largest cardinal.

Figure 1 The bi-interpretable models.
The model
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is in turn bi-interpretable with the extension
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is in turn bi-interpretable with the extension
![]() ${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
adjoining
${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
adjoining
![]() $\lambda $
many atoms. This bi-interpretation can be realized via the construction of
$\lambda $
many atoms. This bi-interpretation can be realized via the construction of
![]() $W{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
described in Section 2 as with Theorem 2.1, but undertaken in
$W{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
described in Section 2 as with Theorem 2.1, but undertaken in
![]() $\mathrm {ZFC}^-$
, where the construction works fine, producing a model of
$\mathrm {ZFC}^-$
, where the construction works fine, producing a model of
![]() $\mathrm {ZFCU}^{-}$
in which
$\mathrm {ZFCU}^{-}$
in which
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
remain inaccessible, with
$\lambda $
remain inaccessible, with
![]() $\lambda $
remaining as the largest cardinal, and the set of urelements has size
$\lambda $
remaining as the largest cardinal, and the set of urelements has size
![]() $\lambda $
. Thus, theories (4) and (5) are bi-interpretable.
$\lambda $
. Thus, theories (4) and (5) are bi-interpretable.
The model
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is bi-interpretable with
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
is bi-interpretable with
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}, \overline {\mathcal {V}}\right \rangle }$
as in Theorem 4.1, where
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}, \overline {\mathcal {V}}\right \rangle }$
as in Theorem 4.1, where
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}=W_{\lambda }$
and
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}=W_{\lambda }$
and
![]() $\overline {\mathcal {V}}$
consists of the subsets of
$\overline {\mathcal {V}}$
consists of the subsets of
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
available in W. The model
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
available in W. The model
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}, \overline {\mathcal {V}}\right \rangle }$
has
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu}, \overline {\mathcal {V}}\right \rangle }$
has
![]() $\lambda $
as its class of ordinals, and
$\lambda $
as its class of ordinals, and
![]() $\kappa $
will still be inaccessible there. The model
$\kappa $
will still be inaccessible there. The model
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
is in turn bi-interpretable with
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
is in turn bi-interpretable with
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A),\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
, adjoining
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A),\mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
, adjoining
![]() $\lambda $
many atoms, because of Theorem 5.1.
$\lambda $
many atoms, because of Theorem 5.1.
The original model
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
is realized as the
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
is realized as the
![]() ${\left \langle H_{\kappa }(A),\mathrel {\varepsilon },\mathcal {H}\right \rangle }$
as defined in
${\left \langle H_{\kappa }(A),\mathrel {\varepsilon },\mathcal {H}\right \rangle }$
as defined in
![]() ${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
, and it can see how it is realized in that way via the interpretation to W and then to
${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
, and it can see how it is realized in that way via the interpretation to W and then to
![]() $W{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. So all five theories are bi-interpretable, as claimed.
$W{\mathopen {\lbrack \!\lbrack }A\mathclose {\rbrack \!\rbrack }}$
. So all five theories are bi-interpretable, as claimed.
Let us also describe how to achieve a direct bi-interpretation of
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
with
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
with
![]() ${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
and hence also with
${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
and hence also with
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A), \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
. We can simply mount an urelement analogue of the unrolling construction, what might be called the urelement unrolling of the model. Specifically, define that an urelement membership code is a well-founded directed graph class relation E with a unique maximal node, which is extensional on all its non-minimal nodes, and where the E-minimal nodes are either elements of A or
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A), \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
. We can simply mount an urelement analogue of the unrolling construction, what might be called the urelement unrolling of the model. Specifically, define that an urelement membership code is a well-founded directed graph class relation E with a unique maximal node, which is extensional on all its non-minimal nodes, and where the E-minimal nodes are either elements of A or
![]() $\varnothing $
. For any set x in the urelement context, the canonical membership code
$\varnothing $
. For any set x in the urelement context, the canonical membership code
![]() ${\left \langle \mathop {\mathrm { TC}}(\{{x}\}),\in \right \rangle }$
is an example, since the
${\left \langle \mathop {\mathrm { TC}}(\{{x}\}),\in \right \rangle }$
is an example, since the
![]() $\in $
-minimal elements of this set will be atoms or
$\in $
-minimal elements of this set will be atoms or
![]() $\varnothing $
. As before, we define an equivalence relation on the codes
$\varnothing $
. As before, we define an equivalence relation on the codes
![]() $E\sim F$
, which holds when they are isomorphic by a map fixing the atoms used as minimal elements. And we define
$E\sim F$
, which holds when they are isomorphic by a map fixing the atoms used as minimal elements. And we define
![]() $E\mathrel {\varepsilon } F$
if there is some
$E\mathrel {\varepsilon } F$
if there is some
![]() $y\mathrel {F} x$
, where x is the maximal node of F, such that
$y\mathrel {F} x$
, where x is the maximal node of F, such that
![]() $E\sim F\downarrow y$
. In the theory KMU+CC, one can verify that these codes work as expected to code higher sets, just as in Theorem 4.1 with the pure membership codes. One shows that the isomorphisms witnessing equivalence are unique, that any two partial initial isomorphisms of codes agree on their common part, and that every two codes admit a maximal partial initial isomorphism. Using the urelement analogues of the arguments made earlier, one can thus verify that the structure
$E\sim F\downarrow y$
. In the theory KMU+CC, one can verify that these codes work as expected to code higher sets, just as in Theorem 4.1 with the pure membership codes. One shows that the isomorphisms witnessing equivalence are unique, that any two partial initial isomorphisms of codes agree on their common part, and that every two codes admit a maximal partial initial isomorphism. Using the urelement analogues of the arguments made earlier, one can thus verify that the structure
![]() ${\left \langle W(A),\mathrel {\varepsilon },\mathcal {W}\right \rangle }$
, where
${\left \langle W(A),\mathrel {\varepsilon },\mathcal {W}\right \rangle }$
, where
![]() $W(A)$
consists of the equivalence classes
$W(A)$
consists of the equivalence classes
![]() $[E]_{\sim }$
of the urelement membership codes, and
$[E]_{\sim }$
of the urelement membership codes, and
![]() $\mathcal {W}$
consists of the classes
$\mathcal {W}$
consists of the classes
![]() $X\subseteq W(A)$
that are realized by a class of codes in
$X\subseteq W(A)$
that are realized by a class of codes in
![]() $\mathcal {H}$
. One gets the power set axiom in
$\mathcal {H}$
. One gets the power set axiom in
![]() ${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
below
${\left \langle W(A),\mathrel {\varepsilon }\right \rangle }$
below
![]() $\lambda $
using that the small classes are closed under power class by the abundant atom axiom. To verify collection, one uses both CC as before and also the part of the abundant atom axiom asserting that the small classes are closed under small unions. The cardinal
$\lambda $
using that the small classes are closed under power class by the abundant atom axiom. To verify collection, one uses both CC as before and also the part of the abundant atom axiom asserting that the small classes are closed under small unions. The cardinal
![]() $\kappa $
arising from
$\kappa $
arising from
![]() $\mathord {\mathrm {Ord}}^V$
is inaccessible in
$\mathord {\mathrm {Ord}}^V$
is inaccessible in
![]() $W(A)$
, as is the cardinal
$W(A)$
, as is the cardinal
![]() $\lambda $
that comes from the class of atoms.
$\lambda $
that comes from the class of atoms.
If one considers only the urelement membership codes arising from small classes, the result is the model
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A), \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
, and if one considers only the small class membership codes (with no urelements), then one realizes
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A), \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}(A)\right \rangle }$
, and if one considers only the small class membership codes (with no urelements), then one realizes
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
. In this way, we can directly interpret in a natural way between any two of these five models.
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
. In this way, we can directly interpret in a natural way between any two of these five models.
Finally, let us observe that we can take only the pure sets and classes of
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
to get the model
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
to get the model
![]() ${\left \langle V,\in ,\mathcal {V}_{\tiny pure}\right \rangle }$
of
${\left \langle V,\in ,\mathcal {V}_{\tiny pure}\right \rangle }$
of
![]() $\mathrm {KM}+\mathrm {CC}$
indicated in the lower left of Figure 1, but what we should like specifically to observe is that this model is not bi-interpretable with the other five models mentioned in the proof of Theorem 6.4. This model has no classes of size larger than
$\mathrm {KM}+\mathrm {CC}$
indicated in the lower left of Figure 1, but what we should like specifically to observe is that this model is not bi-interpretable with the other five models mentioned in the proof of Theorem 6.4. This model has no classes of size larger than
![]() $\kappa $
and has no way to represent the cardinals of
$\kappa $
and has no way to represent the cardinals of
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
and W above
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
and W above
![]() $\kappa $
. If we were to perform the unrolling construction of this model, we would get a model of
$\kappa $
. If we were to perform the unrolling construction of this model, we would get a model of
![]() $\mathrm {ZFC}^-$
in which
$\mathrm {ZFC}^-$
in which
![]() $\kappa $
was the largest cardinal. In fact, it would be
$\kappa $
was the largest cardinal. In fact, it would be
![]() $H_{\kappa ^+}^W=H_{\kappa ^+}^{{\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}}$
, which is considerably smaller than the other models we are considering here.
$H_{\kappa ^+}^W=H_{\kappa ^+}^{{\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}}$
, which is considerably smaller than the other models we are considering here.
7 Second-order reflection in pure set theory
Let us now consider the topic of reflection in models
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of second-order set theory. Of course, we immediately get first-order reflection as with the Lévy–Montague reflection theorem—every first-order statement
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
of second-order set theory. Of course, we immediately get first-order reflection as with the Lévy–Montague reflection theorem—every first-order statement
![]() $\varphi (X)$
that is true in
$\varphi (X)$
that is true in
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
even with a class parameter
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
even with a class parameter
![]() $X\in \mathcal {V}$
is also true at some rank in the cumulative hierarchy
$X\in \mathcal {V}$
is also true at some rank in the cumulative hierarchy
![]() $V_{\lambda }\models \varphi (X\upharpoonright V_{\lambda })$
.
$V_{\lambda }\models \varphi (X\upharpoonright V_{\lambda })$
.
Generalizing this, the second-order reflection principle (evidently first considered in [Reference Bernays1]) is the scheme of assertions that every second order assertion
![]() $\varphi (X)$
true in
$\varphi (X)$
true in
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
is already true in some rank-initial segment of the universe
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
is already true in some rank-initial segment of the universe
![]() $V_{\lambda }\models \varphi (X\cap V_{\lambda })$
. It would be equivalent to say that every
$V_{\lambda }\models \varphi (X\cap V_{\lambda })$
. It would be equivalent to say that every
![]() $\varphi (X)$
true in
$\varphi (X)$
true in
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
is true in some transitive set v, that is, the statement
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
is true in some transitive set v, that is, the statement
![]() $\varphi (X\cap v)$
holds in the structure
$\varphi (X\cap v)$
holds in the structure
![]() ${\left \langle v,\in ,P(v)\right \rangle }$
, equipped with all its subsets. The reason is that by simply including GBC as part of what
${\left \langle v,\in ,P(v)\right \rangle }$
, equipped with all its subsets. The reason is that by simply including GBC as part of what
![]() $\varphi $
asserts, we can thereby assume
$\varphi $
asserts, we can thereby assume
![]() ${\left \langle v,\in ,P(v)\right \rangle }$
is a model of GBC, and since the model has all subsets of v this will be a model of second-order
${\left \langle v,\in ,P(v)\right \rangle }$
is a model of GBC, and since the model has all subsets of v this will be a model of second-order
![]() $\mathrm {ZFC}_2$
, but by Zermelo’s quasi-categoricity theorem, this implies that v must be
$\mathrm {ZFC}_2$
, but by Zermelo’s quasi-categoricity theorem, this implies that v must be
![]() $V_{\kappa }$
for some inaccessible cardinal
$V_{\kappa }$
for some inaccessible cardinal
![]() $\kappa $
. So in fact, the second-order reflection principle is equivalently stated as: every second-order assertion
$\kappa $
. So in fact, the second-order reflection principle is equivalently stated as: every second-order assertion
![]() $\varphi (X)$
true in the full universe
$\varphi (X)$
true in the full universe
![]() ${\left \langle V,\in ,\mathcal {V}\right \rangle }$
reflects to some inaccessible cardinal
${\left \langle V,\in ,\mathcal {V}\right \rangle }$
reflects to some inaccessible cardinal
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }\models \varphi (X\cap V_{\kappa })$
. Note that we can equivalently state reflection as the principle that every formula
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }\models \varphi (X\cap V_{\kappa })$
. Note that we can equivalently state reflection as the principle that every formula
![]() $\varphi (x,X)$
with a free variable x and class parameter X is absolute to some inaccessible
$\varphi (x,X)$
with a free variable x and class parameter X is absolute to some inaccessible
![]() $V_{\kappa }$
, since we can incorporate as a parameter the class of satisfying instances x, and reflecting that class and the fact that it is defined by
$V_{\kappa }$
, since we can incorporate as a parameter the class of satisfying instances x, and reflecting that class and the fact that it is defined by
![]() $\varphi $
amounts to absoluteness of
$\varphi $
amounts to absoluteness of
![]() $\varphi (x,X)$
between
$\varphi (x,X)$
between
![]() $V_{\kappa }$
and V.
$V_{\kappa }$
and V.
By pushing on this inaccessibility argument a little, we get a stationary proper class of inaccessible cardinals. Namely, for any class club
![]() $C\subseteq \mathord {\mathrm {Ord}}$
, we can reflect the assertion that C is a class club down to some inaccessible
$C\subseteq \mathord {\mathrm {Ord}}$
, we can reflect the assertion that C is a class club down to some inaccessible
![]() $V_{\kappa }$
, and from this it follows that
$V_{\kappa }$
, and from this it follows that
![]() $\kappa $
is a limit point of C and hence in C. In other words, second-order reflection implies that every closed unbounded class of cardinals contains an inaccessible cardinal, and this is what it means to say that
$\kappa $
is a limit point of C and hence in C. In other words, second-order reflection implies that every closed unbounded class of cardinals contains an inaccessible cardinal, and this is what it means to say that
![]() $\mathord {\mathrm {Ord}}$
is Mahlo. Pushing still harder achieves even better lower bounds, as follows.
$\mathord {\mathrm {Ord}}$
is Mahlo. Pushing still harder achieves even better lower bounds, as follows.
Theorem 7.1. Assume KM plus the second-order reflection principle. Then for every n there are a stationary proper class of
![]() $\Pi ^1_n$
-indescribable cardinals.
$\Pi ^1_n$
-indescribable cardinals.
Proof Assume KM plus second-order reflection. Fix any class club
![]() $C\subseteq \mathord {\mathrm {Ord}}$
and any class
$C\subseteq \mathord {\mathrm {Ord}}$
and any class
![]() $X\subseteq \mathord {\mathrm {Ord}}$
. By the reflection property, any
$X\subseteq \mathord {\mathrm {Ord}}$
. By the reflection property, any
![]() $\Pi ^1_n$
assertion
$\Pi ^1_n$
assertion
![]() $\varphi (X)$
reflects to some
$\varphi (X)$
reflects to some
![]() $V_{\kappa }$
with
$V_{\kappa }$
with
![]() $\kappa $
inaccessible and in C. By reflecting that property, using a universal
$\kappa $
inaccessible and in C. By reflecting that property, using a universal
![]() $\Pi ^1_n$
predicate, we find such a
$\Pi ^1_n$
predicate, we find such a
![]() $\kappa $
such that every subset
$\kappa $
such that every subset
![]() $Y\subseteq \kappa $
reflects every
$Y\subseteq \kappa $
reflects every
![]() $\Pi ^1_n$
property from
$\Pi ^1_n$
property from
![]() ${\left \langle V_{\kappa },\in ,Y\right \rangle }$
to some smaller inaccessible
${\left \langle V_{\kappa },\in ,Y\right \rangle }$
to some smaller inaccessible
![]() ${\left \langle V_{\gamma },\in ,Y\cap \gamma \right \rangle }$
, with
${\left \langle V_{\gamma },\in ,Y\cap \gamma \right \rangle }$
, with
![]() $\gamma \in C$
. Thus,
$\gamma \in C$
. Thus,
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi ^1_n$
-indescribable and in C. So the class of them is stationary.
$\Pi ^1_n$
-indescribable and in C. So the class of them is stationary.
For a quick upper bound on the strength of second-order reflection, let us observe the following (see also [Reference Solovay, Reinhardt and Kanamori23]).
Theorem 7.2. If
![]() $\kappa $
is a measurable cardinal, then
$\kappa $
is a measurable cardinal, then
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
is a model of
![]() $\mathrm {KM}+\mathrm {CC}$
plus the second-order reflection principle.
$\mathrm {KM}+\mathrm {CC}$
plus the second-order reflection principle.
Proof Suppose that
![]() $\kappa $
is a measurable cardinal and
$\kappa $
is a measurable cardinal and
![]() $\varphi (X)$
holds in
$\varphi (X)$
holds in
![]() $V_{\kappa }$
for some second-order assertion
$V_{\kappa }$
for some second-order assertion
![]() $\varphi $
, with
$\varphi $
, with
![]() $X\subseteq V_{\kappa }$
. Let
$X\subseteq V_{\kappa }$
. Let
![]() $j:V\to M$
be an elementary embedding with critical point
$j:V\to M$
be an elementary embedding with critical point
![]() $\kappa $
. So
$\kappa $
. So
![]() $\varphi (j(X))$
holds in
$\varphi (j(X))$
holds in
![]() $M_{j(\kappa )}$
, equipped with all its subsets in M. But notice that
$M_{j(\kappa )}$
, equipped with all its subsets in M. But notice that
![]() $V_{\kappa }$
and
$V_{\kappa }$
and
![]() $V_{\kappa +1}$
both exist in M, and so M can see that
$V_{\kappa +1}$
both exist in M, and so M can see that
![]() $\varphi (j(X))$
reflects from
$\varphi (j(X))$
reflects from
![]() $M_{j(\kappa )}$
down to the structure
$M_{j(\kappa )}$
down to the structure
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
, since
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
, since
![]() $j(X)\cap V_{\kappa }=X$
. So M thinks the assertion
$j(X)\cap V_{\kappa }=X$
. So M thinks the assertion
![]() $\varphi (j(X))$
reflects to an inaccessible cardinal below
$\varphi (j(X))$
reflects to an inaccessible cardinal below
![]() $j(\kappa )$
. By elementarity, it follows in V that
$j(\kappa )$
. By elementarity, it follows in V that
![]() $\varphi (X)$
must reflect from
$\varphi (X)$
must reflect from
![]() $V_{\kappa }$
to some inaccessible
$V_{\kappa }$
to some inaccessible
![]() $V_{\delta }$
below
$V_{\delta }$
below
![]() $\kappa $
, as desired.
$\kappa $
, as desired.
Kanamori [Reference Kanamori14, Exercise 9.18] shows that an
![]() $\omega $
-Erdős cardinal suffices for this, and this is interesting because these cardinals are consistent with
$\omega $
-Erdős cardinal suffices for this, and this is interesting because these cardinals are consistent with
![]() $V=L$
and consequently the large cardinal upper bound on the strength of second-order reflection is comparatively low in the large cardinal hierarchy, amongst the large cardinals that can exist in L.
$V=L$
and consequently the large cardinal upper bound on the strength of second-order reflection is comparatively low in the large cardinal hierarchy, amongst the large cardinals that can exist in L.
Let us also observe a curiosity, namely, that the second-order reflection principle erases the difference between GBC and KM. Indeed, one even gets global choice, as a consequence of AC for sets only, as well as the principle of class choice CC, all for free as a consequence of second-order reflection. Let GBc be the theory
![]() $\mathrm {GB}+\mathrm {AC}$
, that is, where we omit global choice and have just AC for sets.
$\mathrm {GB}+\mathrm {AC}$
, that is, where we omit global choice and have just AC for sets.
Theorem 7.3. Over Gödel–Bernays set theory
![]() $\mathrm {GBc}$
, the second-order reflection principle implies global choice, second-order class comprehension, and class choice. In short, GBc plus second-order reflection is equivalent to
$\mathrm {GBc}$
, the second-order reflection principle implies global choice, second-order class comprehension, and class choice. In short, GBc plus second-order reflection is equivalent to
![]() $\mathrm {KM}+\mathrm {CC}$
plus second-order reflection. Similarly, in the urelement context
$\mathrm {KM}+\mathrm {CC}$
plus second-order reflection. Similarly, in the urelement context
![]() $\mathrm {GBcU}$
plus second-order reflection is equivalent to
$\mathrm {GBcU}$
plus second-order reflection is equivalent to
![]() $\mathrm {KMU}+\mathrm {CC}$
plus second-order reflection.
$\mathrm {KMU}+\mathrm {CC}$
plus second-order reflection.
Proof Assume GBc and the second-order reflection principle. If there was no global well-order of the universe, or if any particular axiom of KM failed or any instance of CC failed, then this assertion would reflect to some inaccessible
![]() $V_{\kappa }$
. But every such model
$V_{\kappa }$
. But every such model
![]() ${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
satisfies KM+CC, and global choice holds here by the axiom of choice in V. So those failures couldn’t have occurred up in V in the first place. The same idea works in the urelement context (see Section 9), since the reflection set will have to have the form
${\left \langle V_{\kappa },\in ,V_{\kappa +1}\right \rangle }$
satisfies KM+CC, and global choice holds here by the axiom of choice in V. So those failures couldn’t have occurred up in V in the first place. The same idea works in the urelement context (see Section 9), since the reflection set will have to have the form
![]() $H_{\kappa }(w)$
with an inaccessible cardinal
$H_{\kappa }(w)$
with an inaccessible cardinal
![]() $\kappa $
and a set of urelements w, and all such models similarly fulfill
$\kappa $
and a set of urelements w, and all such models similarly fulfill
![]() $\mathrm {KMU}+\mathrm {CC}$
.
$\mathrm {KMU}+\mathrm {CC}$
.
8 Second-order reflective cardinals and supercompactness
We introduce a notion of second-order reflection from higher structures to smaller substructures, which will turn out to characterize the supercompact cardinals.
-
(1) A cardinal
 $\kappa $
is second-order reflective, if every second-order sentence
$\kappa $
is second-order reflective, if every second-order sentence
 $\varphi $
true in some structure M (of any size) with
$\varphi $
true in some structure M (of any size) with
 $\kappa \subseteq M$
in a language of size less than
$\kappa \subseteq M$
in a language of size less than
 $\kappa $
is also true in a first-order elementary substructure
$\kappa $
is also true in a first-order elementary substructure
 $m\prec M$
of size less than
$m\prec M$
of size less than
 $\kappa $
and with
$\kappa $
and with
 $m\cap \kappa \in \kappa $
.
$m\cap \kappa \in \kappa $
. -
(2) The cardinal
 $\kappa $
is second-order
$\kappa $
is second-order
 $\lambda $
-reflective, for a cardinal
$\lambda $
-reflective, for a cardinal
 $\lambda \geq \kappa $
, if such reflection occurs for all models M of size
$\lambda \geq \kappa $
, if such reflection occurs for all models M of size
 $\lambda $
.
$\lambda $
. -
(3) The cardinal
 $\kappa $
is reflective or
$\kappa $
is reflective or
 $\lambda $
-reflective for
$\lambda $
-reflective for
 $\Pi ^1_n$
assertions, if such reflection occurs for all sentences
$\Pi ^1_n$
assertions, if such reflection occurs for all sentences
 $\varphi $
of complexity
$\varphi $
of complexity
 $\Pi ^1_n$
.
$\Pi ^1_n$
.
One can equivalently drop the requirement that m is elementary in M, requiring only that m is a submodel, by Skolemizing the language to make these notions agree. It is also equivalent to consider only finite languages, rather than languages of size less than
![]() $\kappa $
, since one can index the language elements by ordinals below some
$\kappa $
, since one can index the language elements by ordinals below some
![]() $\gamma <\kappa $
, with
$\gamma <\kappa $
, with
![]() $\gamma $
named as a constant, and then
$\gamma $
named as a constant, and then
![]() $m\cap \kappa \in \kappa $
will ensure that all desired indices are in m. One can accommodate individuals
$m\cap \kappa \in \kappa $
will ensure that all desired indices are in m. One can accommodate individuals
![]() $a\in M$
and class parameters
$a\in M$
and class parameters
![]() $X\subseteq M$
into
$X\subseteq M$
into
![]() $\varphi $
simply by including them in the signature
$\varphi $
simply by including them in the signature
![]() ${\left \langle M,a,X,\dots \right \rangle }$
. And it is equivalent to ask for the absoluteness of a formula
${\left \langle M,a,X,\dots \right \rangle }$
. And it is equivalent to ask for the absoluteness of a formula
![]() $\varphi (x)$
between m and M, rather than merely a sentence, simply by including the class of satisfying instances into the language.
$\varphi (x)$
between m and M, rather than merely a sentence, simply by including the class of satisfying instances into the language.
The
![]() $\lambda $
-reflective cardinals have a natural affinity with Magidor’s [Reference Magidor16] characterization of supercompactness, namely, that
$\lambda $
-reflective cardinals have a natural affinity with Magidor’s [Reference Magidor16] characterization of supercompactness, namely, that
![]() $\kappa $
is supercompact if and only if for every ordinal
$\kappa $
is supercompact if and only if for every ordinal
![]() $\lambda \geq \kappa $
there is
$\lambda \geq \kappa $
there is
![]() $\alpha <\kappa $
and an elementary embedding
$\alpha <\kappa $
and an elementary embedding
![]() $j:V_{\alpha }\to V_{\lambda }$
sending its critical point to
$j:V_{\alpha }\to V_{\lambda }$
sending its critical point to
![]() $\kappa $
, and more to the point, an affinity with Magidor’s proof that the smallest supercompact cardinal is the least cardinal
$\kappa $
, and more to the point, an affinity with Magidor’s proof that the smallest supercompact cardinal is the least cardinal
![]() $\kappa $
such that every
$\kappa $
such that every
![]() $\Pi ^1_1$
sentence true in any structure M (in a finite language) is true in a substructure of size less than
$\Pi ^1_1$
sentence true in any structure M (in a finite language) is true in a substructure of size less than
![]() $\kappa $
. Despite the similarity of this hypothesis with our notion of
$\kappa $
. Despite the similarity of this hypothesis with our notion of
![]() $\lambda $
-reflectivity above—it lacks only the requirement that
$\lambda $
-reflectivity above—it lacks only the requirement that
![]() $m\cap \kappa \in \kappa $
—our notion exactly does not appear in [Reference Magidor16]. Nevertheless, as we prove in Theorem 8.2 and Corollary 8.3, the concept of
$m\cap \kappa \in \kappa $
—our notion exactly does not appear in [Reference Magidor16]. Nevertheless, as we prove in Theorem 8.2 and Corollary 8.3, the concept of
![]() $\lambda $
-reflectivity successfully characterizes supercompactness generally, not just for the least supercompact cardinal. Furthermore, Theorem 8.4 provides a level-by-level characterization of the
$\lambda $
-reflectivity successfully characterizes supercompactness generally, not just for the least supercompact cardinal. Furthermore, Theorem 8.4 provides a level-by-level characterization of the
![]() $\lambda $
-reflective cardinals as exactly the nearly
$\lambda $
-reflective cardinals as exactly the nearly
![]() $\lambda $
-supercompact cardinals. Our results can therefore be taken as a refinement of Magidor’s characterizations.
$\lambda $
-supercompact cardinals. Our results can therefore be taken as a refinement of Magidor’s characterizations.
-
(1) Every
 $\lambda $
-supercompact cardinal
$\lambda $
-supercompact cardinal
 $\kappa $
is second-order
$\kappa $
is second-order
 $\lambda $
-reflective.
$\lambda $
-reflective. -
(2) Every cardinal
 $\kappa $
that is
$\kappa $
that is
 $2^{\lambda ^{<\kappa }}\!\!$
-reflective for
$2^{\lambda ^{<\kappa }}\!\!$
-reflective for
 $\Pi ^1_1$
assertions is
$\Pi ^1_1$
assertions is
 $\lambda $
-supercompact.
$\lambda $
-supercompact.
Proof (1) Suppose that
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact, and consider any structure
$\lambda $
-supercompact, and consider any structure
![]() $M={\left \langle \lambda ,R,f,\dots \right \rangle }$
on domain
$M={\left \langle \lambda ,R,f,\dots \right \rangle }$
on domain
![]() $\lambda $
, with some second-order statement
$\lambda $
, with some second-order statement
![]() $\varphi $
being true in M. Let
$\varphi $
being true in M. Let
![]() $j:V\to N$
be a
$j:V\to N$
be a
![]() $\lambda $
-supercompactness embedding. So
$\lambda $
-supercompactness embedding. So
![]() $j(M)={\left \langle j(\lambda ),j(R),j(f),\dots \right \rangle }$
is a structure in N in the same language, and
$j(M)={\left \langle j(\lambda ),j(R),j(f),\dots \right \rangle }$
is a structure in N in the same language, and
![]() $\varphi $
holds in
$\varphi $
holds in
![]() $j(M)$
. Consider the substructure
$j(M)$
. Consider the substructure
![]() , which is isomorphic to M by the pointwise application map
, which is isomorphic to M by the pointwise application map
![]() $x\mapsto j(x)$
. In particular,
$x\mapsto j(x)$
. In particular,
![]() $\varphi $
is also true in
$\varphi $
is also true in
![]() , and this is visible in N, which has all the same subsets of this structure as V. Since j is elementary, it follows also that
, and this is visible in N, which has all the same subsets of this structure as V. Since j is elementary, it follows also that
![]() is a first-order elementary substructure of
is a first-order elementary substructure of
![]() $j(M)$
. It has size
$j(M)$
. It has size
![]() $\lambda $
, which is less than
$\lambda $
, which is less than
![]() $j(\kappa )$
, and is in N, and furthermore,
$j(\kappa )$
, and is in N, and furthermore,
![]() . So in N, we have found an elementary substructure of
. So in N, we have found an elementary substructure of
![]() $j(M)$
of size less than
$j(M)$
of size less than
![]() $j(\kappa )$
, whose intersection with
$j(\kappa )$
, whose intersection with
![]() $j(\kappa )$
is an ordinal, to which
$j(\kappa )$
is an ordinal, to which
![]() $\varphi $
reflects. By elementarity, it follows in V that there must be such an elementary substructure m of M of size less than which
$\varphi $
reflects. By elementarity, it follows in V that there must be such an elementary substructure m of M of size less than which
![]() $\varphi $
reflects, as desired. So
$\varphi $
reflects, as desired. So
![]() $\kappa $
is second-order
$\kappa $
is second-order
![]() $\lambda $
-reflective.
$\lambda $
-reflective.
(2) Suppose that
![]() $\kappa $
is
$\kappa $
is
![]() $2^{\lambda ^{<\kappa }}$
-reflective for
$2^{\lambda ^{<\kappa }}$
-reflective for
![]() $\Pi ^1_1$
assertions, and let M be the structure
$\Pi ^1_1$
assertions, and let M be the structure
![]() ${\left \langle H_{(\lambda ^{<\kappa })^+},\in ,\kappa ,\lambda \right \rangle }$
, which is a transitive structure of size
${\left \langle H_{(\lambda ^{<\kappa })^+},\in ,\kappa ,\lambda \right \rangle }$
, which is a transitive structure of size
![]() $2^{\lambda ^{<\kappa }}$
, containing
$2^{\lambda ^{<\kappa }}$
, containing
![]() $\lambda $
,
$\lambda $
,
![]() $P_{\kappa }\lambda $
, and every subset of
$P_{\kappa }\lambda $
, and every subset of
![]() $P_{\kappa }\lambda $
, and having
$P_{\kappa }\lambda $
, and having
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
as named constants. The question whether there is a normal fine measure on
$\lambda $
as named constants. The question whether there is a normal fine measure on
![]() $P_{\kappa }\lambda $
is expressible as a second-order assertion
$P_{\kappa }\lambda $
is expressible as a second-order assertion
![]() $\varphi $
in this structure, since any such measure is determined by a subset
$\varphi $
in this structure, since any such measure is determined by a subset
![]() $\mu \subseteq M$
, picking out the measure-one subsets of
$\mu \subseteq M$
, picking out the measure-one subsets of
![]() $P_{\kappa }\lambda $
and asserting that these sets constitute a normal fine measure. Normality and fineness are both first-order properties of
$P_{\kappa }\lambda $
and asserting that these sets constitute a normal fine measure. Normality and fineness are both first-order properties of
![]() $\mu $
over M, and so the assertion that
$\mu $
over M, and so the assertion that
![]() $\kappa $
is not
$\kappa $
is not
![]() $\lambda $
-supercompact is
$\lambda $
-supercompact is
![]() $\Pi ^1_1$
-expressible over M. So if
$\Pi ^1_1$
-expressible over M. So if
![]() $\kappa $
is not
$\kappa $
is not
![]() $\lambda $
-supercompact, then this reflects to some elementary substructure
$\lambda $
-supercompact, then this reflects to some elementary substructure
![]() $m\prec M$
of size less than
$m\prec M$
of size less than
![]() $\kappa $
with
$\kappa $
with
![]() $m\cap \kappa \in \kappa $
—but note that m will not be transitive. Let
$m\cap \kappa \in \kappa $
—but note that m will not be transitive. Let
![]() $s=m\cap \lambda $
, which is an element of
$s=m\cap \lambda $
, which is an element of
![]() $P_{\kappa }\lambda $
, and let
$P_{\kappa }\lambda $
, and let
![]() $\mu _m=\{{X\in m\mid X\subseteq P_{\kappa }\lambda , s\in X}\}$
be the family of sets in m containing s, the principal filter. The model m can see that this measure is
$\mu _m=\{{X\in m\mid X\subseteq P_{\kappa }\lambda , s\in X}\}$
be the family of sets in m containing s, the principal filter. The model m can see that this measure is
![]() $\kappa $
-complete, because if
$\kappa $
-complete, because if
![]() $\vec X={\left \langle X_{\alpha }\mid \alpha <\beta \right \rangle }$
is a
$\vec X={\left \langle X_{\alpha }\mid \alpha <\beta \right \rangle }$
is a
![]() $\beta $
-sequence of subsets
$\beta $
-sequence of subsets
![]() $X_{\alpha }\subseteq P_{\kappa }\lambda $
that m thinks are all in
$X_{\alpha }\subseteq P_{\kappa }\lambda $
that m thinks are all in
![]() $\mu _m$
, then
$\mu _m$
, then
![]() $\beta \in m$
and consequently every
$\beta \in m$
and consequently every
![]() $\alpha <\beta $
is in m, and so every
$\alpha <\beta $
is in m, and so every
![]() $X_{\alpha }$
is in m. Thus,
$X_{\alpha }$
is in m. Thus,
![]() $s\in X_{\alpha }$
for every
$s\in X_{\alpha }$
for every
![]() $\alpha <\beta $
and hence also
$\alpha <\beta $
and hence also
![]() $s\in \bigcap _{\alpha <\beta }X_{\alpha }$
, which is
$s\in \bigcap _{\alpha <\beta }X_{\alpha }$
, which is
![]() $\bigcap \vec X$
as computed in m. Since every ordinal
$\bigcap \vec X$
as computed in m. Since every ordinal
![]() $\alpha <\lambda $
in m is in s, it follows that m will think that
$\alpha <\lambda $
in m is in s, it follows that m will think that
![]() $\mu _m$
is fine. And since every element of s is in m, it follows that m will think that every regressive function is constant on a
$\mu _m$
is fine. And since every element of s is in m, it follows that m will think that every regressive function is constant on a
![]() $\mu _m$
-measure one set. So m thinks that
$\mu _m$
-measure one set. So m thinks that
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact, contrary to the reflection assumption.
$\lambda $
-supercompact, contrary to the reflection assumption.
Corollary 8.3. The following are equivalent:
-
(1)
 $\kappa $
is second-order reflective.
$\kappa $
is second-order reflective. -
(2)
 $\kappa $
is reflective for
$\kappa $
is reflective for
 $\Pi ^1_1$
assertions.
$\Pi ^1_1$
assertions. -
(3)
 $\kappa $
is a supercompact cardinal.
$\kappa $
is a supercompact cardinal.
Proof Theorem 8.2 shows that supercompactness implies reflectivity level-by-level, and we only need reflectivity for
![]() $\Pi ^1_1$
assertions at
$\Pi ^1_1$
assertions at
![]() $2^{\lambda ^{<\kappa }}$
to get
$2^{\lambda ^{<\kappa }}$
to get
![]() $\lambda $
-supercompactness.
$\lambda $
-supercompactness.
The second-order reflectivity hierarchy is therefore simply a different, finer manner of stratifying the supercompactness hierarchy. Indeed, let us mount a somewhat more delicate analysis, which will enable us to provide an exact level-by-level equivalence using the notion of near supercompactness. Specifically, Schanker [Reference Schanker18–Reference Schanker20], in dissertation work undertaken with the first author of this paper, defines that a cardinal
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\lambda $
-supercompact, if for every
$\lambda $
-supercompact, if for every
![]() $A\subseteq \lambda $
there is a transitive model
$A\subseteq \lambda $
there is a transitive model
![]() $M\models \mathrm {ZFC}^-$
, closed under
$M\models \mathrm {ZFC}^-$
, closed under
![]() -sequences, with
-sequences, with
![]() $\lambda ,A\in M$
, and there is an elementary embedding
$\lambda ,A\in M$
, and there is an elementary embedding
![]() $j:M\to N$
with critical point
$j:M\to N$
with critical point
![]() $\kappa $
for which
$\kappa $
for which
![]() $\lambda <j(\kappa )$
and
$\lambda <j(\kappa )$
and
![]() . He proves an abundance of equivalent characterizations in [Reference Schanker19, Theorem 2.1.3], one of which is the normal filter property:
. He proves an abundance of equivalent characterizations in [Reference Schanker19, Theorem 2.1.3], one of which is the normal filter property:
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\lambda $
-supercompact if and only if for every collection M having at most
$\lambda $
-supercompact if and only if for every collection M having at most
![]() $\lambda $
many subsets of
$\lambda $
many subsets of
![]() $P_{\kappa }\lambda $
and at most
$P_{\kappa }\lambda $
and at most
![]() $\lambda $
many functions
$\lambda $
many functions
![]() $f:P_{\kappa }\lambda \to \lambda $
, there is a
$f:P_{\kappa }\lambda \to \lambda $
, there is a
![]() $\kappa $
-complete fine filter on
$\kappa $
-complete fine filter on
![]() $P_{\kappa }\lambda $
measuring every subset in M that is also M-normal, meaning that every regressive function f in M is constant on a measure one set.
$P_{\kappa }\lambda $
measuring every subset in M that is also M-normal, meaning that every regressive function f in M is constant on a measure one set.
Theorem 8.4. Assume
![]() $\lambda =\lambda ^{<\kappa }$
. Then the following are equivalent:
$\lambda =\lambda ^{<\kappa }$
. Then the following are equivalent:
-
(1)
 $\kappa $
is
$\kappa $
is
 $\lambda $
-reflective for
$\lambda $
-reflective for
 $\Pi ^1_1$
assertions.
$\Pi ^1_1$
assertions. -
(2)
 $\kappa $
is nearly
$\kappa $
is nearly
 $\lambda $
-supercompact.
$\lambda $
-supercompact.
Every nearly
![]() $\lambda $
-supercompact cardinal
$\lambda $
-supercompact cardinal
![]() $\kappa $
is also nearly
$\kappa $
is also nearly
![]() $\lambda ^{<\kappa }$
-supercompact, by [Reference Schanker19, Lemma 2.1.5], and so we could have alternatively stated this theorem as the claim: a cardinal
$\lambda ^{<\kappa }$
-supercompact, by [Reference Schanker19, Lemma 2.1.5], and so we could have alternatively stated this theorem as the claim: a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda ^{<\kappa }$
-reflective for
$\lambda ^{<\kappa }$
-reflective for
![]() $\Pi ^1_1$
if and only if it is nearly
$\Pi ^1_1$
if and only if it is nearly
![]() $\lambda $
-supercompact.
$\lambda $
-supercompact.
Proof Suppose that
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\lambda $
-supercompact and
$\lambda $
-supercompact and
![]() $\lambda =\lambda ^{<\kappa }$
. Consider any first-order structure
$\lambda =\lambda ^{<\kappa }$
. Consider any first-order structure
![]() $\Lambda ={\left \langle \lambda ,R,f,\dots \right \rangle }$
with a signature of size less than
$\Lambda ={\left \langle \lambda ,R,f,\dots \right \rangle }$
with a signature of size less than
![]() $\kappa $
, satisfying a
$\kappa $
, satisfying a
![]() $\Pi ^1_1$
sentence
$\Pi ^1_1$
sentence
![]() $\varphi $
. We may place this structure into a transitive model
$\varphi $
. We may place this structure into a transitive model
![]() $M\prec H_{\lambda ^+}$
of size
$M\prec H_{\lambda ^+}$
of size
![]() $\lambda $
, closed under
$\lambda $
, closed under
![]() -sequences. So there is an elementary embedding
-sequences. So there is an elementary embedding
![]() $j:M\to N$
with critical point
$j:M\to N$
with critical point
![]() $\kappa $
and
$\kappa $
and
![]() . It follows that
. It follows that
![]() is in N, isomorphic to
is in N, isomorphic to
![]() $\Lambda $
, and a first-order elementary substructure of
$\Lambda $
, and a first-order elementary substructure of
![]() $j(\Lambda )$
. Since
$j(\Lambda )$
. Since
![]() $\varphi $
is
$\varphi $
is
![]() $\Pi ^1_1$
and is actually true in
$\Pi ^1_1$
and is actually true in
![]() $\Lambda $
, it will also be true of
$\Lambda $
, it will also be true of
![]() in N. (This step of the argument would not necessarily work for more complicated assertions, since N may not have all subsets of
in N. (This step of the argument would not necessarily work for more complicated assertions, since N may not have all subsets of
![]() .) So N thinks that
.) So N thinks that
![]() $\varphi $
reflects from
$\varphi $
reflects from
![]() $j(\Lambda )$
to a small elementary substructure, whose intersection with
$j(\Lambda )$
to a small elementary substructure, whose intersection with
![]() $j(\kappa )$
is an ordinal. By elementarity, M thinks the same of
$j(\kappa )$
is an ordinal. By elementarity, M thinks the same of
![]() $\Lambda $
, and since
$\Lambda $
, and since
![]() $M\prec H_{\lambda ^+}$
, this is also true in V. So
$M\prec H_{\lambda ^+}$
, this is also true in V. So
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-reflective for
$\lambda $
-reflective for
![]() $\Pi ^1_1$
assertions.
$\Pi ^1_1$
assertions.
Conversely, suppose now that
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-reflective for
$\lambda $
-reflective for
![]() $\Pi ^1_1$
assertions, and consider any family of at most
$\Pi ^1_1$
assertions, and consider any family of at most
![]() $\lambda $
many subsets of
$\lambda $
many subsets of
![]() $P_{\kappa }\lambda $
and
$P_{\kappa }\lambda $
and
![]() $\lambda $
many functions
$\lambda $
many functions
![]() $f:P_{\kappa }\lambda \to \lambda $
. Place these into a transitive structure
$f:P_{\kappa }\lambda \to \lambda $
. Place these into a transitive structure
![]() $M\prec H_{\lambda ^+}$
of size
$M\prec H_{\lambda ^+}$
of size
![]() $\lambda $
and closed under
$\lambda $
and closed under
![]() -sequences. The nonexistence of an M-normal fine
-sequences. The nonexistence of an M-normal fine
![]() $\kappa $
-complete filter measuring every set in M is expressed by a
$\kappa $
-complete filter measuring every set in M is expressed by a
![]() $\Pi ^1_1$
sentence over M. So if indeed there were no such filter, this would reflect to some elementary substructure
$\Pi ^1_1$
sentence over M. So if indeed there were no such filter, this would reflect to some elementary substructure
![]() $m\prec M$
of size less than
$m\prec M$
of size less than
![]() $\kappa $
with
$\kappa $
with
![]() $m\cap \kappa \in \kappa $
. As in the proof of Theorem 8.2, we may use the set
$m\cap \kappa \in \kappa $
. As in the proof of Theorem 8.2, we may use the set
![]() $s=m\cap \lambda $
to define a filter
$s=m\cap \lambda $
to define a filter
![]() $\mu _m=\{{X\in m\mid X\subseteq P_{\kappa }\lambda , s\in X}\}$
, and this will be fine, m-normal, and
$\mu _m=\{{X\in m\mid X\subseteq P_{\kappa }\lambda , s\in X}\}$
, and this will be fine, m-normal, and
![]() $\kappa $
-complete. So m thinks that there is an m-normal fine
$\kappa $
-complete. So m thinks that there is an m-normal fine
![]() $\kappa $
-complete filter, contrary to the reflection. So
$\kappa $
-complete filter, contrary to the reflection. So
![]() $\kappa $
must have had the normal fine filter property originally and thus it is nearly
$\kappa $
must have had the normal fine filter property originally and thus it is nearly
![]() $\lambda $
-supercompact.
$\lambda $
-supercompact.
Theorem 8.4 thus provides a more refined analysis than Theorem 8.2 in the characterization of the cardinals that are
![]() $\lambda $
-reflective for
$\lambda $
-reflective for
![]() $\Pi ^1_1$
assertions, which are exactly the nearly
$\Pi ^1_1$
assertions, which are exactly the nearly
![]() $\lambda $
-supercompact cardinals. This theorem is part of a constellation of closely related, similar results in the research literature, including [Reference Carr2, Theorems 3.5 and 4.7], [Reference Cody3, Theorem 1.4], and [Reference Hayut and Magidor12, Lemma 2.8].
$\lambda $
-supercompact cardinals. This theorem is part of a constellation of closely related, similar results in the research literature, including [Reference Carr2, Theorems 3.5 and 4.7], [Reference Cody3, Theorem 1.4], and [Reference Hayut and Magidor12, Lemma 2.8].
In the KM context, we say that
![]() $\kappa $
is second-order X-reflective, for any class
$\kappa $
is second-order X-reflective, for any class
![]() $X\supseteq \kappa $
, if any such assertion
$X\supseteq \kappa $
, if any such assertion
![]() $\varphi $
true in a class structure M on domain X is also true in a set structure
$\varphi $
true in a class structure M on domain X is also true in a set structure
![]() $m\prec M$
of size less than
$m\prec M$
of size less than
![]() $\kappa $
with
$\kappa $
with
![]() $m\cap \kappa \in \kappa $
. And similarly with X-reflective for
$m\cap \kappa \in \kappa $
. And similarly with X-reflective for
![]() $\Pi ^1_1$
assertions, restricting the complexity of
$\Pi ^1_1$
assertions, restricting the complexity of
![]() $\varphi $
. If
$\varphi $
. If
![]() $\kappa $
is
$\kappa $
is
![]() $\mathord {\mathrm { Ord}}$
-reflective for
$\mathord {\mathrm { Ord}}$
-reflective for
![]() $\Pi ^1_1$
, then it is
$\Pi ^1_1$
, then it is
![]() $\lambda $
-reflective for
$\lambda $
-reflective for
![]() $\Pi ^1_1$
for all
$\Pi ^1_1$
for all
![]() $\lambda \geq \kappa $
, and so by Theorem 8.2, it follows that
$\lambda \geq \kappa $
, and so by Theorem 8.2, it follows that
![]() $\kappa $
is supercompact. In this sense,
$\kappa $
is supercompact. In this sense,
![]() $\mathord {\mathrm {Ord}}$
-reflectivity is a strengthening of supercompactness.
$\mathord {\mathrm {Ord}}$
-reflectivity is a strengthening of supercompactness.
9 Second-order reflection with urelements
Let us now analyze the situation of second-order reflection in the urelement context. A model
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
of second-order urelement set theory GBCU satisfies the second-order reflection principle if every second-order statement
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
of second-order urelement set theory GBCU satisfies the second-order reflection principle if every second-order statement
![]() $\varphi (X)$
true in that model of some class parameter
$\varphi (X)$
true in that model of some class parameter
![]() $X\in \mathcal {V}$
reflects to some transitive set
$X\in \mathcal {V}$
reflects to some transitive set
![]() $v\in V(A)$
, meaning that
$v\in V(A)$
, meaning that
![]() ${\left \langle v,\in ,P(v)\right \rangle }\models \varphi (X\cap v)$
. By including
${\left \langle v,\in ,P(v)\right \rangle }\models \varphi (X\cap v)$
. By including
![]() $\mathrm {GBCU}$
as part of
$\mathrm {GBCU}$
as part of
![]() $\varphi $
, we may assume
$\varphi $
, we may assume
![]() ${\left \langle v,\in ,P(v)\right \rangle }\models \mathrm {GBCU}$
, and from this it follows that v must have the form
${\left \langle v,\in ,P(v)\right \rangle }\models \mathrm {GBCU}$
, and from this it follows that v must have the form
![]() $H_{\kappa }(w)$
for some inaccessible cardinal
$H_{\kappa }(w)$
for some inaccessible cardinal
![]() $\kappa $
and set of urelements w, because v will be closed under power sets and will have to contain all the size-less-than-
$\kappa $
and set of urelements w, because v will be closed under power sets and will have to contain all the size-less-than-
![]() $\kappa $
subsets of itself, where
$\kappa $
subsets of itself, where
![]() $\kappa =v\cap \mathord {\mathrm {Ord}}$
, which will consequently be inaccessible. (Note that when w has size
$\kappa =v\cap \mathord {\mathrm {Ord}}$
, which will consequently be inaccessible. (Note that when w has size
![]() $\kappa $
or larger, this is not the same as
$\kappa $
or larger, this is not the same as
![]() $V_{\kappa }(w)$
, since w itself has rank
$V_{\kappa }(w)$
, since w itself has rank
![]() $1$
and would appear as a set, but in
$1$
and would appear as a set, but in
![]() $H_{\kappa }(w)$
it would be a proper class.) The second author proved in [Reference Yao25] that KMU with at most
$H_{\kappa }(w)$
it would be a proper class.) The second author proved in [Reference Yao25] that KMU with at most
![]() $\mathord {\mathrm {Ord}}$
many urelements and second-order reflection is bi-interpretable with KM plus second-order reflection. The main contribution of this article, in contrast, will be to observe the dramatic increase in large-cardinal strength of second-order reflection when there are more than
$\mathord {\mathrm {Ord}}$
many urelements and second-order reflection is bi-interpretable with KM plus second-order reflection. The main contribution of this article, in contrast, will be to observe the dramatic increase in large-cardinal strength of second-order reflection when there are more than
![]() $\mathord {\mathrm {Ord}}$
many urelements.
$\mathord {\mathrm {Ord}}$
many urelements.
Let us begin with the observation that from supercompactness, we can produce models of urelement set theory with more than
![]() $\mathord {\mathrm {Ord}}$
many urelements, yet with second-order reflection. This observation is one of the core ideas and main results proved by the second author in [Reference Yao25, Reference Yao26], showing that if
$\mathord {\mathrm {Ord}}$
many urelements, yet with second-order reflection. This observation is one of the core ideas and main results proved by the second author in [Reference Yao25, Reference Yao26], showing that if
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa ^+$
-supercompact, then there is a model of KMU with strictly more than
$\kappa ^+$
-supercompact, then there is a model of KMU with strictly more than
![]() $\mathord {\mathrm {Ord}}$
many urelements and the second-order reflection principle. Here, we generalize the observation to higher levels of supercompactness.
$\mathord {\mathrm {Ord}}$
many urelements and the second-order reflection principle. Here, we generalize the observation to higher levels of supercompactness.
Theorem 9.1. Assume V satisfies
![]() $\mathrm {ZFC}+\kappa $
is
$\mathrm {ZFC}+\kappa $
is
![]() $\lambda $
-supercompact, where
$\lambda $
-supercompact, where
![]() $\lambda>\kappa $
. In the interpreted model
$\lambda>\kappa $
. In the interpreted model
![]() $V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
of ZFCU with
$V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
of ZFCU with
![]() $\lambda $
many urelements A, the hereditary model
$\lambda $
many urelements A, the hereditary model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of
![]() $\mathrm {KMU}+\mathrm {CC}$
plus second-order reflection with more than
$\mathrm {KMU}+\mathrm {CC}$
plus second-order reflection with more than
![]() $\mathord {\mathrm {Ord}}$
many urelements, indeed,
$\mathord {\mathrm {Ord}}$
many urelements, indeed,
![]() $\lambda $
many.
$\lambda $
many.
Proof Let
![]() $V(A)$
be the extension of V by adding
$V(A)$
be the extension of V by adding
![]() $\lambda $
many urelements, isomorphic to the model
$\lambda $
many urelements, isomorphic to the model
![]() $V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
as interpreted inside V. We consider
$V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
as interpreted inside V. We consider
![]() $H_{\kappa }(A)$
as defined in
$H_{\kappa }(A)$
as defined in
![]() $V(A)$
, with its isomorphic copy
$V(A)$
, with its isomorphic copy
![]() $H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
interpreted in V, taking
$H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
interpreted in V, taking
![]() $\mathcal {H}$
as the power set of
$\mathcal {H}$
as the power set of
![]() $H_{\kappa }(A)$
in
$H_{\kappa }(A)$
in
![]() $V(A)$
. (We can build
$V(A)$
. (We can build
![]() $H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
directly in V by starting with the urelement objects
$H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
directly in V by starting with the urelement objects
![]() ${\left \langle 0,\alpha \right \rangle }$
for
${\left \langle 0,\alpha \right \rangle }$
for
![]() $\alpha <\lambda $
and then closing under the operation
$\alpha <\lambda $
and then closing under the operation
![]() $y\subseteq H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}\implies {\left \langle 1,y\right \rangle }\in H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
for y of size less than
$y\subseteq H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}\implies {\left \langle 1,y\right \rangle }\in H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
for y of size less than
![]() $\kappa $
.) This is a model of
$\kappa $
.) This is a model of
![]() $\mathrm {KMU}+\mathrm {CC}$
by Theorem 6.1, and since
$\mathrm {KMU}+\mathrm {CC}$
by Theorem 6.1, and since
![]() $\lambda>\kappa $
, the model thinks the class of urelements is strictly larger than
$\lambda>\kappa $
, the model thinks the class of urelements is strictly larger than
![]() $\mathord {\mathrm {Ord}}$
. By replacing
$\mathord {\mathrm {Ord}}$
. By replacing
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda ^{<\kappa }$
, we may assume
$\lambda ^{<\kappa }$
, we may assume
![]() $\lambda =\lambda ^{<\kappa }$
. The structure
$\lambda =\lambda ^{<\kappa }$
. The structure
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, has size
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, has size
![]() $\lambda $
, and so by Theorem 8.2, every second-order statement
$\lambda $
, and so by Theorem 8.2, every second-order statement
![]() $\varphi (X)$
true in that structure reflects to some first-order elementary substructure m of size less than
$\varphi (X)$
true in that structure reflects to some first-order elementary substructure m of size less than
![]() $\kappa $
, whose intersection with
$\kappa $
, whose intersection with
![]() $\kappa $
is an ordinal
$\kappa $
is an ordinal
![]() $m\cap \kappa \in m$
. This implies m is transitive, since if
$m\cap \kappa \in m$
. This implies m is transitive, since if
![]() $x\in m$
, then m can enumerate it in some order type
$x\in m$
, then m can enumerate it in some order type
![]() $\gamma $
, which must be less than
$\gamma $
, which must be less than
![]() $\kappa $
, but since
$\kappa $
, but since
![]() $m\cap \kappa \in \kappa $
, it follows that
$m\cap \kappa \in \kappa $
, it follows that
![]() $\gamma \subseteq m$
and so every element of x is also in m. So it is transitive, and so we have verified second-order reflection in this model.
$\gamma \subseteq m$
and so every element of x is also in m. So it is transitive, and so we have verified second-order reflection in this model.
Next, we improve on the hypothesis by observing that the proof can be undertaken with the weaker assumption that
![]() $\kappa $
is merely nearly
$\kappa $
is merely nearly
![]() $\lambda $
-supercompact, instead of
$\lambda $
-supercompact, instead of
![]() $\lambda $
-supercompact. We simply place
$\lambda $
-supercompact. We simply place
![]() $H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
into a transitive
$H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
into a transitive
![]() $M\prec H_{\lambda ^+}$
of size
$M\prec H_{\lambda ^+}$
of size
![]() $\lambda $
, closed under
$\lambda $
, closed under
![]() -sequences, and then apply Theorem 8.4. This provides:
-sequences, and then apply Theorem 8.4. This provides:
Theorem 9.2. Assume V satisfies
![]() $\mathrm {ZFC}+\kappa $
is nearly
$\mathrm {ZFC}+\kappa $
is nearly
![]() $\lambda $
-supercompact, where
$\lambda $
-supercompact, where
![]() $\lambda>\kappa $
. In the interpreted model
$\lambda>\kappa $
. In the interpreted model
![]() $V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
of ZFCU with
$V{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
of ZFCU with
![]() $\lambda $
many urelements A, the hereditary model
$\lambda $
many urelements A, the hereditary model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
is a model of
![]() $\mathrm {KMU}+\mathrm {CC}$
plus
$\mathrm {KMU}+\mathrm {CC}$
plus
![]() $\Pi ^1_1$
reflection with more than
$\Pi ^1_1$
reflection with more than
![]() $\mathord {\mathrm {Ord}}$
many urelements, indeed,
$\mathord {\mathrm {Ord}}$
many urelements, indeed,
![]() $\lambda $
many.
$\lambda $
many.
A consequence of Theorem 9.2 is that to produce a model of
![]() $\mathrm {KMU}+\mathrm {CC}$
with strictly more than
$\mathrm {KMU}+\mathrm {CC}$
with strictly more than
![]() $\mathord {\mathrm {Ord}}$
many atoms and second-order reflection, it to have a nearly
$\mathord {\mathrm {Ord}}$
many atoms and second-order reflection, it to have a nearly
![]() $\kappa ^+$
-supercompact cardinal, which is strictly weaker than
$\kappa ^+$
-supercompact cardinal, which is strictly weaker than
![]() $\kappa ^+$
-supercompact, although this hypothesis remains very strong in large cardinal terms—for example, by [Reference Schanker19] it implies
$\kappa ^+$
-supercompact, although this hypothesis remains very strong in large cardinal terms—for example, by [Reference Schanker19] it implies
![]() $\mathrm {AD}^{L({\mathbb R})}$
.
$\mathrm {AD}^{L({\mathbb R})}$
.
10 Second-order reflection with abundant atoms implies supercompact
We come now finally to the main result of this article, where we aim to prove conversely that supercompactness is required for second-order reflection in the context of urelement set theory when there are abundant atoms, even just for
![]() $\Pi ^1_1$
reflection.
$\Pi ^1_1$
reflection.
Main Theorem 10.1. The following theories are bi-interpretable.
-
(0)
 $\mathrm {GBc}+{}$
abundant atom axiom
$\mathrm {GBc}+{}$
abundant atom axiom
 $+$
second-order reflection.
$+$
second-order reflection. -
(1)
 $\mathrm {KMU}+\mathrm {CC}+{}$
abundant atom axiom
$\mathrm {KMU}+\mathrm {CC}+{}$
abundant atom axiom
 $+$
second-order reflection.
$+$
second-order reflection. -
(2)
 $\mathrm {KM}+\mathrm {CC}+\kappa \text { is supercompact and second-order }\mathord {\mathrm {Ord}}\text {-reflective.}$
$\mathrm {KM}+\mathrm {CC}+\kappa \text { is supercompact and second-order }\mathord {\mathrm {Ord}}\text {-reflective.}$
-
(3)
 $\mathrm {KMU}+\mathrm {CC}+\mathord {\mathrm {Ord}}\text { many atoms}+\kappa $
is supercompact and second-order
$\mathrm {KMU}+\mathrm {CC}+\mathord {\mathrm {Ord}}\text { many atoms}+\kappa $
is supercompact and second-order
 $\mathord {\mathrm {Ord}} \text {-reflective.}$
$\mathord {\mathrm {Ord}} \text {-reflective.}$
-
(4)
 $\mathrm {ZFC}^-+\kappa $
is
$\mathrm {ZFC}^-+\kappa $
is
 -supercompact and (moreover) second-order
-supercompact and (moreover) second-order
 $\lambda $
-reflective, where
$\lambda $
-reflective, where
 $\lambda $
is the largest cardinal and inaccessible.
$\lambda $
is the largest cardinal and inaccessible. -
(5)
 $\mathrm {ZFCU}^{-}+\lambda $
many atoms
$\mathrm {ZFCU}^{-}+\lambda $
many atoms
 ${}+\kappa $
is
${}+\kappa $
is
 -supercompact and (moreover) second-order
-supercompact and (moreover) second-order
 $\lambda $
-reflective, where
$\lambda $
-reflective, where
 $\lambda $
is the largest cardinal and inaccessible.
$\lambda $
is the largest cardinal and inaccessible.
Proof Several of the theories are redundantly stated in order to highlight the presence of supercompactness; namely, as we mentioned earlier every second-order
![]() $\mathord {\mathrm {Ord}}$
-reflective cardinal is automatically supercompact, and similarly every second-order
$\mathord {\mathrm {Ord}}$
-reflective cardinal is automatically supercompact, and similarly every second-order
![]() $\lambda $
-reflective cardinal for an inaccessible cardinal
$\lambda $
-reflective cardinal for an inaccessible cardinal
![]() $\lambda $
is also
$\lambda $
is also
![]() -supercompact by Theorem 8.2. Furthermore, theories (0) and (1) are provably identical in light of Theorem 7.3. For the remaining bi-interpretations, we shall use the same interpretations as in Theorem 6.4, while observing how the stronger reflection properties here manifest in the different models.
-supercompact by Theorem 8.2. Furthermore, theories (0) and (1) are provably identical in light of Theorem 7.3. For the remaining bi-interpretations, we shall use the same interpretations as in Theorem 6.4, while observing how the stronger reflection properties here manifest in the different models.

Figure 2 Supercompactness bi-interpretation.
Let us start at the lower right of Figure 2 with the model
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
of
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
of
![]() $\mathrm {KM}+\mathrm {CC}$
with the abundant atom axiom and second-order reflection. We observe first that the second-order reflection property ensures that
$\mathrm {KM}+\mathrm {CC}$
with the abundant atom axiom and second-order reflection. We observe first that the second-order reflection property ensures that
![]() $\kappa $
is second-order
$\kappa $
is second-order
![]() $\lambda $
-reflective in W. Notice that the concept of
$\lambda $
-reflective in W. Notice that the concept of
![]() $\lambda $
-reflective makes sense as a scheme in a model of
$\lambda $
-reflective makes sense as a scheme in a model of
![]() $\mathrm {ZFC}^-$
, since it refers only to objects of size
$\mathrm {ZFC}^-$
, since it refers only to objects of size
![]() $\lambda $
. But any structure M in W of size
$\lambda $
. But any structure M in W of size
![]() $\lambda $
is coded by a class in
$\lambda $
is coded by a class in
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, which has the same subclasses there as the subsets available in W. We can equip this with a first-order truth predicate, and by the second-order reflection principle every second-order assertion in that expanded structure will reflect to a transitive set in
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
, which has the same subclasses there as the subsets available in W. We can equip this with a first-order truth predicate, and by the second-order reflection principle every second-order assertion in that expanded structure will reflect to a transitive set in
![]() $V(A)$
, which because of the truth predicate will also be a first-order elementary substructure in W of size less than
$V(A)$
, which because of the truth predicate will also be a first-order elementary substructure in W of size less than
![]() $\kappa $
. The transitivity of the substructure in
$\kappa $
. The transitivity of the substructure in
![]() $V(A)$
translates to transitivity-below-
$V(A)$
translates to transitivity-below-
![]() $\kappa $
in W (urelements in substructure in
$\kappa $
in W (urelements in substructure in
![]() $V(A)$
will give rise possibly to nontransitivity above
$V(A)$
will give rise possibly to nontransitivity above
![]() $\kappa $
). So
$\kappa $
). So
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-reflective in W. From this it follows that
$\lambda $
-reflective in W. From this it follows that
![]() $\kappa $
is
$\kappa $
is
![]() -supercompact in W, which implies both that
-supercompact in W, which implies both that
![]() $\kappa $
is fully supercompact in
$\kappa $
is fully supercompact in
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
, which is simply
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
, which is simply
![]() $W_{\lambda }$
, and also that
$W_{\lambda }$
, and also that
![]() $\kappa $
is
$\kappa $
is
![]() $\mathord {\mathrm {Ord}}$
-reflective in
$\mathord {\mathrm {Ord}}$
-reflective in
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
, which itself translates back to
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
, which itself translates back to
![]() $\lambda $
-reflectivity in W. The supercompactness of
$\lambda $
-reflectivity in W. The supercompactness of
![]() $\kappa $
carries over through the bi-interpretations to
$\kappa $
carries over through the bi-interpretations to
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A)$
and to
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A)$
and to
![]() $W(A)$
, and conversely, and so we’ve got all the theories just as we want them.
$W(A)$
, and conversely, and so we’ve got all the theories just as we want them.
The second-order reflection principle, we claim, does not necessarily hold in
![]() ${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
, since
${\left \langle {\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}, \mathrel {\mkern 3mu\overline {\mkern -3mu\in \mkern -1.5mu}\mkern 1.5mu},\overline {\mathcal {V}}\right \rangle }$
, since
![]() $\lambda $
could be the next inaccessible above
$\lambda $
could be the next inaccessible above
![]() $\kappa $
, and this would violate second-order reflection, which implies that the inaccessible cardinals (and the
$\kappa $
, and this would violate second-order reflection, which implies that the inaccessible cardinals (and the
![]() $\Pi ^1_n$
-indescribable cardinals, etc.) form a stationary proper class. This situation arises if
$\Pi ^1_n$
-indescribable cardinals, etc.) form a stationary proper class. This situation arises if
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact for the next inaccessible cardinal
$\lambda $
-supercompact for the next inaccessible cardinal
![]() $\lambda $
and we form
$\lambda $
and we form
![]() $H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
as in Theorem 9.1. This would be a model of theory (1), but the corresponding
$H_{\kappa }{\mathopen {\lbrack \!\lbrack } \lambda \mathclose {\rbrack \!\rbrack }}$
as in Theorem 9.1. This would be a model of theory (1), but the corresponding
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
would have no inaccessible cardinals above
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
would have no inaccessible cardinals above
![]() $\kappa $
and hence not fulfill second-order reflection.
$\kappa $
and hence not fulfill second-order reflection.
We get an analogous version of the theorem for
![]() $\Pi ^1_1$
-reflectivity as follows.
$\Pi ^1_1$
-reflectivity as follows.
Main Theorem 10.2 (
 $\Pi ^1_1$
variation)
$\Pi ^1_1$
variation)
The following theories are bi-interpretable.
-
(1)
 $\mathrm {KMU}+\mathrm {CC}+{}$
abundant atom axiom
$\mathrm {KMU}+\mathrm {CC}+{}$
abundant atom axiom
 $+\Pi ^1_1$
reflection.
$+\Pi ^1_1$
reflection. -
(2)
 $\mathrm {KM}+\mathrm {CC}+\kappa \text { is supercompact and }\mathord {\mathrm {Ord}}\text {-reflective for }\Pi ^1_1$
.
$\mathrm {KM}+\mathrm {CC}+\kappa \text { is supercompact and }\mathord {\mathrm {Ord}}\text {-reflective for }\Pi ^1_1$
. -
(3)
 $\mathrm {KMU}+\mathrm {CC}+\mathord {\mathrm {Ord}}\text { many atoms}+\kappa \text { supercompact and }\mathord {\mathrm {Ord}}\text {-reflective for }\Pi ^1_1$
.
$\mathrm {KMU}+\mathrm {CC}+\mathord {\mathrm {Ord}}\text { many atoms}+\kappa \text { supercompact and }\mathord {\mathrm {Ord}}\text {-reflective for }\Pi ^1_1$
. -
(4)
 $\mathrm {ZFC}^-+\kappa $
is
$\mathrm {ZFC}^-+\kappa $
is
 -supercompact and (moreover) nearly
-supercompact and (moreover) nearly
 $\lambda $
-supercompact, where
$\lambda $
-supercompact, where
 $\lambda>\kappa $
is the largest cardinal and inaccessible.
$\lambda>\kappa $
is the largest cardinal and inaccessible. -
(5)
 $\mathrm {ZFCU}^{-}+\lambda \text { many atoms}+\kappa $
is
$\mathrm {ZFCU}^{-}+\lambda \text { many atoms}+\kappa $
is
 -supercompact and (moreover) nearly
-supercompact and (moreover) nearly
 $\lambda $
-supercompact, where
$\lambda $
-supercompact, where
 $\lambda>\kappa $
is the largest cardinal and inaccessible.
$\lambda>\kappa $
is the largest cardinal and inaccessible.
The point is that
![]() $\Pi ^1_1$
-reflection in the original model carries over to
$\Pi ^1_1$
-reflection in the original model carries over to
![]() $\Pi ^1_1$
reflection in the other models (and conversely), ensuring in W that
$\Pi ^1_1$
reflection in the other models (and conversely), ensuring in W that
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-reflective for
$\lambda $
-reflective for
![]() $\Pi ^1_1$
assertions, which is equivalent to it being nearly
$\Pi ^1_1$
assertions, which is equivalent to it being nearly
![]() $\lambda $
-supercompact by Theorem 8.4.
$\lambda $
-supercompact by Theorem 8.4.
Let us finally also address the central question left open in [Reference Yao25], concerning the strength of KMU with second-order reflection and “more than
![]() $\mathord {\mathrm {Ord}}$
many atoms.” Yao had used a
$\mathord {\mathrm {Ord}}$
many atoms.” Yao had used a
![]() $\kappa ^+$
-supercompact cardinal
$\kappa ^+$
-supercompact cardinal
![]() $\kappa $
in order to produce a model of this theory, and the question is whether supercompactness is required, and specifically whether the large cardinal requirements will exceed the large cardinal notions consistent with
$\kappa $
in order to produce a model of this theory, and the question is whether supercompactness is required, and specifically whether the large cardinal requirements will exceed the large cardinal notions consistent with
![]() $V=L$
.
$V=L$
.
First, we know by Theorem 9.2 that for
![]() $\Pi ^1_1$
reflection it suffices to have merely a nearly
$\Pi ^1_1$
reflection it suffices to have merely a nearly
![]() $\kappa ^+$
-supercompact cardinal
$\kappa ^+$
-supercompact cardinal
![]() $\kappa $
, and since this is strictly weaker than
$\kappa $
, and since this is strictly weaker than
![]() $\kappa ^+$
-supercompactness, this shows that full
$\kappa ^+$
-supercompactness, this shows that full
![]() $\kappa ^+$
-supercompactness is not required for this amount of reflection.
$\kappa ^+$
-supercompactness is not required for this amount of reflection.
Meanwhile, second, the hypothesis that there is a nearly
![]() $\kappa ^+$
-supercompact cardinal
$\kappa ^+$
-supercompact cardinal
![]() $\kappa $
is still quite strong—by [Reference Schanker19] this hypothesis (with
$\kappa $
is still quite strong—by [Reference Schanker19] this hypothesis (with
![]() $2^{\kappa }=\kappa ^+$
) implies
$2^{\kappa }=\kappa ^+$
) implies
![]() $\mathrm {AD}^{L({\mathbb R})}$
over ZFC, which brings us to a strong realm of the large cardinal hierarchy. We can prove the following equiconsistency:
$\mathrm {AD}^{L({\mathbb R})}$
over ZFC, which brings us to a strong realm of the large cardinal hierarchy. We can prove the following equiconsistency:
Theorem 10.3. The following theories are mutually interpretable, hence also equiconsistent:
-
(1)
 $\mathrm {KMU}+\mathrm {CC}+\mathrm {more\ than\ }\mathord {\mathrm {Ord}}\ \mathrm { many\ atoms}+\Pi ^1_1\mathrm {-reflection.}$
$\mathrm {KMU}+\mathrm {CC}+\mathrm {more\ than\ }\mathord {\mathrm {Ord}}\ \mathrm { many\ atoms}+\Pi ^1_1\mathrm {-reflection.}$
-
(2)
 $\mathrm {ZFC}^-+\kappa $
is nearly
$\mathrm {ZFC}^-+\kappa $
is nearly
 $\kappa ^+$
-supercompact.
$\kappa ^+$
-supercompact.
Proof Suppose that
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
is a model of the first theory. Let
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
is a model of the first theory. Let
![]() ${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
be the model of
${\left \langle W,\mathrel {\varepsilon }\right \rangle }$
be the model of
![]() $\mathrm {ZFC}^-$
obtained by the unrolling construction. Let
$\mathrm {ZFC}^-$
obtained by the unrolling construction. Let
![]() $\kappa $
be the cardinal in W that results from a membership code coding the class
$\kappa $
be the cardinal in W that results from a membership code coding the class
![]() $\mathord {\mathrm {Ord}}^V$
itself. This will be an inaccessible cardinal in W, because
$\mathord {\mathrm {Ord}}^V$
itself. This will be an inaccessible cardinal in W, because
![]() $V(A)$
thinks that
$V(A)$
thinks that
![]() $\mathord {\mathrm {Ord}}$
is closed under power sets and regular with respect to class in
$\mathord {\mathrm {Ord}}$
is closed under power sets and regular with respect to class in
![]() $\mathcal {V}$
. Since A has size larger than
$\mathcal {V}$
. Since A has size larger than
![]() $\mathord {\mathrm {Ord}}$
, however, there will cardinals in W strictly larger than
$\mathord {\mathrm {Ord}}$
, however, there will cardinals in W strictly larger than
![]() $\kappa $
, so
$\kappa $
, so
![]() $\lambda =\kappa ^+$
will exist in W (and perhaps many more depending on how many proper class cardinalities there are in
$\lambda =\kappa ^+$
will exist in W (and perhaps many more depending on how many proper class cardinalities there are in
![]() $\mathcal {V}$
). The argument of Theorem 10.1 shows that
$\mathcal {V}$
). The argument of Theorem 10.1 shows that
![]() $\kappa $
is reflective for
$\kappa $
is reflective for
![]() $\Pi ^1_1$
assertions in W and hence nearly
$\Pi ^1_1$
assertions in W and hence nearly
![]() $\lambda $
-supercompact there, providing an interpreted model of the first theory.
$\lambda $
-supercompact there, providing an interpreted model of the first theory.
Conversely, if
![]() ${\left \langle W,\in \right \rangle }$
is a model of the second theory, where
${\left \langle W,\in \right \rangle }$
is a model of the second theory, where
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\kappa ^+$
-supercompact, then we may form the interpreted model
$\kappa ^+$
-supercompact, then we may form the interpreted model
![]() $W{\mathopen {\lbrack \!\lbrack }\kappa ^+\mathclose {\rbrack \!\rbrack }}$
, view it as adjoining a set of
$W{\mathopen {\lbrack \!\lbrack }\kappa ^+\mathclose {\rbrack \!\rbrack }}$
, view it as adjoining a set of
![]() $\kappa ^+$
many urelements
$\kappa ^+$
many urelements
![]() $W(A)$
, and then interpret the model
$W(A)$
, and then interpret the model
![]() ${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, where
${\left \langle H_{\kappa }(A),\in ,\mathcal {H}\right \rangle }$
, where
![]() $\mathcal {H}$
consists of the subsets
$\mathcal {H}$
consists of the subsets
![]() $X\subseteq H_{\kappa }(A)$
that are available in
$X\subseteq H_{\kappa }(A)$
that are available in
![]() $W(A)$
. This is a model of
$W(A)$
. This is a model of
![]() $\mathrm {KMU}+\mathrm {CC}$
with
$\mathrm {KMU}+\mathrm {CC}$
with
![]() $\mathord {\mathrm {Ord}}=\kappa $
and
$\mathord {\mathrm {Ord}}=\kappa $
and
![]() $\kappa ^+$
many atoms. The fact that
$\kappa ^+$
many atoms. The fact that
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\kappa ^+$
-supercompact in W implies the reflection principle for
$\kappa ^+$
-supercompact in W implies the reflection principle for
![]() $\Pi ^1_1$
assertions in the hereditary model, providing a model of the first theory.
$\Pi ^1_1$
assertions in the hereditary model, providing a model of the first theory.
We could achieve a bi-interpretation if we specifically add to the first theory that there are precisely
![]() $\mathord {\mathrm {Ord}}^+$
many atoms, meaning that the class of atoms is not equinumerous with
$\mathord {\mathrm {Ord}}^+$
many atoms, meaning that the class of atoms is not equinumerous with
![]() $\mathord {\mathrm {Ord}}$
, but every proper class is bijective with
$\mathord {\mathrm {Ord}}$
, but every proper class is bijective with
![]() $\mathord {\mathrm {Ord}}$
or with the class of all atoms.
$\mathord {\mathrm {Ord}}$
or with the class of all atoms.
Although the hypothesis that
![]() $\kappa $
is nearly
$\kappa $
is nearly
![]() $\kappa ^+$
-supercompact is strong in ZFC, we are unsure how much of this large cardinal strength can be established in
$\kappa ^+$
-supercompact is strong in ZFC, we are unsure how much of this large cardinal strength can be established in
![]() $\mathrm {ZFC}^-$
. We conjecture, however, that even in the
$\mathrm {ZFC}^-$
. We conjecture, however, that even in the
![]() $\mathrm {ZFC}^-$
context this hypothesis will imply that there is an inner model of ZFC with a measurable cardinal and probably much more; we leave this problem for another time.
$\mathrm {ZFC}^-$
context this hypothesis will imply that there is an inner model of ZFC with a measurable cardinal and probably much more; we leave this problem for another time.
11 Concluding philosophical remarks
How shall we consider urelements in set theory? Historically, set theory in the main has largely abandoned urelements in its fundamental theories, replacing the early urelement set theories with pure set theories such as ZF and ZFC, a development that one can easily explain on structuralist grounds (a point made also in [Reference Hamkins11, Section 8.4]). Namely, since all the mathematical structures that early set theorists wanted to build with urelements, such as number systems or geometric spaces, have found isomorphic copies within the pure sets, and since structuralists do not care which particular objects will be used to constitute a mathematical structure, considering it only as invariant under isomorphism, the urelements are seen as inessential. Indeed, a mathematician who favors urelements on the grounds that some mathematical objects at bottom are not sets and should not be represented with sets can be seen as preoccupied with a misguided anti-structuralist concern, one that, according to structuralism, is irrelevant for mathematical advance.
Furthermore, the bi-interpretability of many natural formulations of urelement set theory with corresponding pure set theories, as in Theorems 2.1 and 5.1, is itself an explanation of precisely how those particular urelement conceptions can be dispensed with in the foundations of mathematics—any mathematical structure to be found in the urelement set theories can be found via the bi-interpretation also in the corresponding pure set theories. And Theorems 6.4 and 10.1 show that this remains true even when one adds abundant urelements and second-order reflection.
If urelement set theories are to play an indispensable role in the foundations of mathematics, therefore, it must not be with those theories, but rather with urelement set theories that are not bi-interpretable with a pure set theory and perhaps not interpretable at all in any pure set theory. But in this case, it would seem that the urelement set theories must involve much stranger sets of urelements, neither well-orderable nor even equinumerous with any pure set. The mathematical structures built on such domains will not be isomorphic with any structure to be found amongst the pure sets. But what are these strange urelements that give rise to these weird sets? One wants an explanation for why we should need or expect to find such sets in the foundations of mathematics. What mathematical structures will they represent?
In second-order urelement set theory, the abundant classes of urelements are perhaps second-order instances of such strange classes, since they are not equinumerous with any class of pure sets. Indeed, the non-equivalence of the class well-order principle with the
![]() $\mathord {\mathrm {Ord}}$
-enumeration of the universe (equivalently expressed by the so-called limitation of size principle) opens to the door to the possibility of strictly more than
$\mathord {\mathrm {Ord}}$
-enumeration of the universe (equivalently expressed by the so-called limitation of size principle) opens to the door to the possibility of strictly more than
![]() $\mathord {\mathrm {Ord}}$
many atoms, even when they are well-orderable, with the abundant atom axiom simply carrying this to an extreme. Such urelement universes are short and fat—overflowing in width with abundant atoms but limited in height with comparatively fewer ordinals. Precisely because of this, perhaps the main lesson of Theorem 6.4 is that the presence of so many urelements simply indicates that one hasn’t continued the cumulative hierarchy high enough. One should add more ordinals on top of the universe, continuing the rank hierarchy to higher levels, and the abundant atoms available tell you exactly how to do this. Indeed, the unrolling constructions of
$\mathord {\mathrm {Ord}}$
many atoms, even when they are well-orderable, with the abundant atom axiom simply carrying this to an extreme. Such urelement universes are short and fat—overflowing in width with abundant atoms but limited in height with comparatively fewer ordinals. Precisely because of this, perhaps the main lesson of Theorem 6.4 is that the presence of so many urelements simply indicates that one hasn’t continued the cumulative hierarchy high enough. One should add more ordinals on top of the universe, continuing the rank hierarchy to higher levels, and the abundant atoms available tell you exactly how to do this. Indeed, the unrolling constructions of
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
and W from the model
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}$
and W from the model
![]() ${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
are exactly implementing this idea of continuing to build the ordinals and rank levels higher. The result is a model
${\left \langle V(A),\in ,\mathcal {V}\right \rangle }$
are exactly implementing this idea of continuing to build the ordinals and rank levels higher. The result is a model
![]() ${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A)$
in which the same class of atoms now has type
${\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}(A)$
in which the same class of atoms now has type
![]() $\mathord {\mathrm {Ord}}$
, which is to say, the new higher class of ordinals
$\mathord {\mathrm {Ord}}$
, which is to say, the new higher class of ordinals
![]() $\mathord {\mathrm {Ord}}^{{\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}}$
, or even forms a set as in
$\mathord {\mathrm {Ord}}^{{\mkern 3.5mu\overline {\mkern -3.5muV\mkern -.5mu}\mkern .5mu}}$
, or even forms a set as in
![]() $W(A)$
, with more ordinals still. From this perspective, the abundant atom axiom reveals the set-theoretic universe as an unfinished project—it should have been built taller. The weaker hypothesis of having a well-ordered class of strictly more than
$W(A)$
, with more ordinals still. From this perspective, the abundant atom axiom reveals the set-theoretic universe as an unfinished project—it should have been built taller. The weaker hypothesis of having a well-ordered class of strictly more than
![]() $\mathord {\mathrm {Ord}}$
many urelements is similarly unnatural, a sign that one simply has not continued the cumulative hierarchy high enough.
$\mathord {\mathrm {Ord}}$
many urelements is similarly unnatural, a sign that one simply has not continued the cumulative hierarchy high enough.
Where does this leave us? If urelements are to be well-orderable, then we should have at most
![]() $\mathord {\mathrm {Ord}}$
of them, or else it is a sign that we have not properly built the cumulative hierarchy of pure sets; but if we have at most
$\mathord {\mathrm {Ord}}$
of them, or else it is a sign that we have not properly built the cumulative hierarchy of pure sets; but if we have at most
![]() $\mathord {\mathrm {Ord}}$
of them, then we don’t need them at all, since having
$\mathord {\mathrm {Ord}}$
of them, then we don’t need them at all, since having
![]() $\mathord {\mathrm {Ord}}$
many atoms (or fewer) is bi-interpretable with the pure set theories. So if urelements are to play a role in the foundations of mathematics, it must be that they are not well-orderable, and furthermore there must be sets of them that are not equinumerous with any pure set.
$\mathord {\mathrm {Ord}}$
many atoms (or fewer) is bi-interpretable with the pure set theories. So if urelements are to play a role in the foundations of mathematics, it must be that they are not well-orderable, and furthermore there must be sets of them that are not equinumerous with any pure set.
Acknowledgments
The authors are grateful to the anonymous referee for extremely detailed, helpful comments. Commentary about this article can be made on the first author’s blog at http://jdh.hamkins.org/second-order-reflection-with-abundant-urelements.