Article contents
Precipitous towers of normal filters
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we investigate towers of normal filters. These towers were first used by Woodin (see [15]). Woodin proved that if δ is a Woodin cardinal and P is the full stationary tower up to δ (P<δ) or the countable version (Q<δ), then the generic ultrapower is closed under < δ sequences (so the generic ultrapower is well-founded) ([14]). We show that if ℙ is a tower of height δ, δ supercompact, and the filters generating ℙ are the club filter restricted to a stationary set, then the generic ultrapower is well-founded (ℙ is precipitous). We also give some examples of non-precipitous towers. We also show that every normal filter can be extended to a V-ultrafilter with well-founded ultrapower in some generic extension of V (assuming large cardinals). Similarly for any tower of inaccessible height. This is accomplished by showing that there is a stationary set that projects to the filter or the tower and then forcing with P<δ below this stationary set.
An important idea in our proof of precipitousness (Theorem 6.4) has the following form in Woodin's proof. If 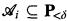 are maximal antichains (i Є ω and δ Woodin) then there is a κ < δ such that each Ai ∩ Vκ is semiproper, i.e.,
are maximal antichains (i Є ω and δ Woodin) then there is a κ < δ such that each Ai ∩ Vκ is semiproper, i.e.,
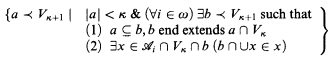
contains a club (relative to ∣ a∣ < κ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 8
- Cited by




