Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T16:05:50.467Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SET-THEORETIC STRENGTH OF ELLIS’ THEOREM AND THE EXISTENCE OF FREE IDEMPOTENT ULTRAFILTERS ON ω

Published online by Cambridge University Press:  01 August 2018

ELEFTHERIOS TACHTSIS
ELEFTHERIOS TACHTSIS*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF THE AEGEAN KARLOVASSI 83200, SAMOS, GREECEE-mail:ltah@aegean.gr
Get access Rights & Permissions [Opens in a new window]

Abstract

Ellis’ Theorem (i.e., “every compact Hausdorff right topological semigroup has an idempotent element”) is known to be proved only under the assumption of the full Axiom of Choice (AC); AC is used in the proof in the disguise of Zorn’s Lemma.

In this article, we prove that in ZF, Ellis’ Theorem follows from the Boolean Prime Ideal Theorem (BPI), and hence is strictly weaker than AC in ZF. In fact, we establish that BPI implies the formally stronger (than Ellis’ Theorem) statement “for every family 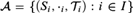${\cal A} = \{ ({S_i},{ \cdot _i},{{\cal T}_i}):i \in I\}$ of nontrivial compact Hausdorff right topological semigroups, there exists a function f with domain I such that 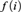$f\left( i \right)$ is an idempotent of 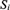${S_i}$, for all 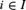$i \in I$”, which in turn implies ACfin (i.e., AC for sets of nonempty finite sets).

Furthermore, we prove that in ZFA, the Axiom of Multiple Choice (MC) implies Ellis’ Theorem for abelian semigroups (i.e., “every compact Hausdorff right topological abelian semigroup has an idempotent element”) and that the strictly weaker than MC (in ZFA) principle LW (i.e., “every linearly ordered set can be well-ordered”) implies Ellis’ Theorem for linearly orderable semigroups (i.e., “every compact Hausdorff right topological linearly orderable semigroup has an idempotent element”); thus the latter formally weaker versions of Ellis’ Theorem are strictly weaker than BPI in ZFA. Yet, it is shown that no choice is required in order to prove Ellis’ Theorem for well-orderable semigroups.

We also show that each one of the (strictly weaker than AC) statements “the Tychonoff product 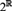$2^{\Cal R} $ is compact and Loeb” and 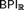$BPI_{\Cal R}$ (BPI for filters on ${\Cal R}$) implies “there exists a free idempotent ultrafilter on ω” (which in turn is not provable in ZF). Moreover, we prove that the latter statement does not imply 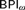$BP{I_\omega }$ (BPI for filters on ω) in ZF, hence it does not imply any of 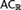$AC_{\Cal R} $ (AC for sets of nonempty sets of reals) and 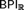$BPI_{\Cal R} $ in ZF, either.

In addition, we prove that the statements “there exists a free ultrafilter on ω”, “there exists a free ultrafilter on ω which is not idempotent”, and “for every IP set 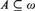$A \subseteq \omega$, there exists a free ultrafilter 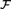${\cal F}$ on ω such that 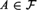$A \in {\cal F}$” are pairwise equivalent in ZF.

Keywords

Primary 03E25Secondary 03E3554D3054D8054H20axiom of choiceweak axioms of choicecompact Hausdorff right topological semigroup (resp. abelian semigroup, linearly orderable semigroup)idempotent elementEllis’ TheoremEllis’ Theorem for abelian semigroups (resp. for linearly orderable semigroups)Stone spacefree idempotent ultrafilter on ωpermutation model of ZFAforcing model of ZF
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 551 - 571
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arhangel’skii, A. and Tkachenko, M., Topological Groups and Related Structures, Atlantis Press/World Scientific, Amsterdam–Paris, 2008.CrossRefGoogle Scholar
Blass, A., Ramsey’s Theorem in the hierarchy of choice principles, this Journal, vol. 42 (1977), no. 3, pp. 387–390.Google Scholar
Blass, A., Ultrafilters: Where topological dynamics = algebra = combinatorics. Topology Proceedings, vol. 18 (1993), pp. 33–56.Google Scholar
Comfort, W. W., Some recent applications of ultrafilters to topology, General Topology and its Relations to Modern Analysis and Algebra IV, Proceedings of the Fourth Prague Topological Symposium, 1976, Part A: Invited Papers (Novák, J., editor), Lecture Notes in Mathematics, vol. 609, Springer, Berlin, 1977, pp. 34–42.Google Scholar
Di Nasso, M. and Tachtsis, E., Idempotent ultrafilters without Zorn’s lemma. Proceedings of the American Mathematical Society, vol. 146 (2018), no. 1, pp. 397–411.CrossRefGoogle Scholar
Fossy, J. and Morillon, M., The Baire category property and some notions of compactness. Journal of the London Mathematical Society, vol. 57 (1998), pp. 1–19.CrossRefGoogle Scholar
Hall, E. J., Keremedis, K., and Tachtsis, E., The existence of free ultrafilters on ω does not imply the extension of filters on ω to ultrafilters. Mathematical Logic Quarterly, vol. 59 (2013), no. 4–5, pp. 258–267.CrossRefGoogle Scholar
Henle, J. M., Mathias, A. R. D., and Woodin, W. H., A barren extension, Methods in Mathematical Logic (Di Prisco, C. A., editor), Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, Berlin, 1985, pp. 195–207.CrossRefGoogle Scholar
Herrlich, H., Axiom of Choice, Lecture Notes in Mathematics, vol. 1876, Springer, Berlin Heidelberg, 2006.Google Scholar
Herrlich, H., Keremedis, K., and Tachtsis, E., Remarks on the Stone spaces of the integers and the reals without AC. Bulletin of the Polish Academy of Sciences Mathematics, vol. 59 (2011), no. 2, pp. 101–114.CrossRefGoogle Scholar
Hindman, N., The existence of certain ultrafilters on N and a conjecture of Graham and Rothschild. Proceedings of the American Mathematical Society, vol. 36 (1972), no. 2, pp. 341–346.Google Scholar
Hindman, N., Finite sums from sequences within cells of a partition of N. Journal of Combinatorial Theory, Series A, vol. 17 (1974), pp. 1–11.CrossRefGoogle Scholar
Hindman, N. and Strauss, D., Algebra in the Stone–Čech Compactification. Theory and Applications, second ed., Walter de Gruyter GmbH & Co. KG, Berlin, 2012.Google Scholar
Howard, P. and Rubin, J. E., Consequences of the Axiom of Choice, Mathematical Surveys and Monographs, vol. 59, American Mathematical Society, Providence, RI, 1998. Consequences of the Axiom of Choice Project Homepage: http://consequences.emich.edu/conseq.htm.CrossRefGoogle Scholar
Jech, T. J., The Axiom of Choice, Studies in Logic and the Foundations of Mathematics, vol. 75, North-Holland, Amsterdam, 1973.Google Scholar
Jech, T. J., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Keremedis, K., Tychonoff products of two-element sets and some weakenings of the Boolean prime ideal theorem. Bulletin of the Polish Academy of Sciences Mathematics, vol. 53 (2005), no. 4, pp. 349–359.CrossRefGoogle Scholar
Keremedis, K. and Tachtsis, E., Some weak forms of the axiom of choice restricted to the real line. Mathematical Logic Quarterly, vol. 47 (2001), no. 3, pp. 413–422.3.0.CO;2-4>CrossRefGoogle Scholar
Keremedis, K. and Tachtsis, E., On Loeb and weakly Loeb Hausdorff spaces. Scientiae Mathematicae Japonicae, vol. 53 (2001), no. 2, pp. 247–251.Google Scholar
Kunen, K., Set Theory. An Introduction to Independence Proofs, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, Amsterdam, 1980.Google Scholar
Loeb, P. A., A new proof of the Tychonoff theorem. American Mathematical Monthly, vol. 72 (1965), pp. 711–717CrossRefGoogle Scholar