Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-07-03T15:27:14.275Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rules of proof in the pure functional calculus of the first order

Published online by Cambridge University Press:  12 March 2014

Andrzej Mostowski
Andrzej Mostowski*
Affiliation:
University of Warsaw
Get access Rights & Permissions [Opens in a new window]

Extract

We consider here the pure functional calculus of first order 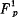as formulated by Church.

Church, l.c., p. 79, gives the definition of the validity of a formula in a given set I of individuals and shows that a formula is provable in 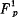if and only if it is valid in every non-empty set I. The definition of validity is preceded by the definition of a value of a formula; the notion of a value is the basic “semantical” notion in terms of which all other semantical notions are definable.

The notion of a value of a formula retains its meaning also in the case when the set I is empty. We have only to remember that if I is empty, then an m-ary propositional function (i.e. a function from the m-th cartesian power Im to the set {f, t}) is the empty set. It then follows easily that the value of each well-formed formula with free individual variables is the empty set. The values of wffs without free variables are on the contrary either f or t. Indeed, if B has the unique free variable c and ϕ is the value of B, then the value of (c)B according to the definition given by Church is the propositional constant f or t according as ϕ(j) is f for at least one j in I or not. Since, however, there is no j in I, the condition ϕ(j) = t for all j in I is vacuously satisfied and hence the value of (c)B is t.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 16 , Issue 2 , June 1951 , pp. 107 - 111
Copyright
Copyright © Association for Symbolic Logic 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Church, Alonzo, Introduction to mathematical logic, Part I. Annals of mathematics studies Number 13, Princeton, 1944Google Scholar.

2 A quantifier is vacuous if it is followed by an expression in which the variable bound by the quantifier is not free. Cf. Quine, Willard Van Orman, Mathematical logic, Cambridge 1947, p. 74Google Scholar.

3 A different set of rules for the functional calculus, such that theorems obtained by these rules are valid in each set I whether empty or not, has been given by Jaśkowski. Cf. Jaśkowski, Stanisław, On the rules of suppositions informal logic, Studia logica. Number 1, Warszawa 1934, §5Google Scholar.

4 In the sense defined by Quine, l.c. p. 79.

5 Quine, l.c., p. 88.

6 I am indebted for this remark to Mr. Grzegorczyk, Dr. H. Hiz, and Mr. Janiczak.