Article contents
Omitting types: application to recursion theory
Published online by Cambridge University Press: 12 March 2014
Extract
Omitting-types theorems have been useful in model theory to construct models with special characteristics. For instance, one method of proving the ω-completeness theorem of Henkin [10] and Orey [20] involves constructing a model that omits the type {x ≠ 0, x ≠ 1, x ≠ 2,···} (i.e., {x ≠ 0, x ≠ 1, x ≠ 2,···} is not satisfiable in the model). Our purpose in this paper is to illustrate uses of omitting-types theorems in recursion theory. The Gandy-Kreisel-Tait Theorem [7] is the most well-known example. This theorem characterizes the class of hyperarithmetical sets as the intersection of all ω-models of analysis (the so-called hard core of analysis). The usual way to prove that a nonhyperarithmetical set does not belong to the hard core is to construct an ω-model of analysis that omits the type representing the set (Application 1). We will find basis results for 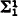 and s —
and s — 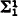 sets that are stronger than results previously known (Applications 2 and 3). The question of how far the natural hierarchy of hyperjumps extends was first settled by a forcing argument (Sacks) and subsequently by a compactness argument (Kripke, Richter). Another problem solved by a forcing argument (Sacks) and then by a compactness argument (Friedman-Jensen) was the characterization of the countable admissible ordinals as the relativized ω1's. Using omitting-types technique, we will supply a third kind of proof of these results (Applications 4 and 5). S. Simpson made a significant contribution in simplifying the proof of the latter result, with the interesting side effect that Friedman's result on ordinals in models of set theory is immediate (Application 6). One approach to abstract recursiveness and hyperarithmeticity on a countable set is to tenuously identify the set with the natural numbers. This approach is equivalent to other approaches to abstract recursion (Application 7). This last result may also be proved by a forcing method.
sets that are stronger than results previously known (Applications 2 and 3). The question of how far the natural hierarchy of hyperjumps extends was first settled by a forcing argument (Sacks) and subsequently by a compactness argument (Kripke, Richter). Another problem solved by a forcing argument (Sacks) and then by a compactness argument (Friedman-Jensen) was the characterization of the countable admissible ordinals as the relativized ω1's. Using omitting-types technique, we will supply a third kind of proof of these results (Applications 4 and 5). S. Simpson made a significant contribution in simplifying the proof of the latter result, with the interesting side effect that Friedman's result on ordinals in models of set theory is immediate (Application 6). One approach to abstract recursiveness and hyperarithmeticity on a countable set is to tenuously identify the set with the natural numbers. This approach is equivalent to other approaches to abstract recursion (Application 7). This last result may also be proved by a forcing method.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 14
- Cited by




