Hostname: page-component-84b7d79bbc-l82ql Total loading time: 0 Render date: 2024-07-25T18:46:38.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Natural models and Ackermann-type set theories1

Published online by Cambridge University Press:  12 March 2014

John Lake
John Lake*
Affiliation:
Polytechnic of the South Bank, London SE1 OAA, England
Get access Rights & Permissions [Opens in a new window]

Extract

Our results concern the natural models of Ackermann-type set theories, but they can also be viewed as results about the definability of ordinals in certain sets.

Ackermann's set theory A was introduced in [1] and it is now formulated in the first order predicate calculus with identity, using ∈ for membership and an individual constant V for the class of all sets. We use the letters ϕ, χ, θ, and χ to stand for formulae which do not contain V and capital Greek letters to stand for any formulae. Then, the axioms of A* are the universal closures of

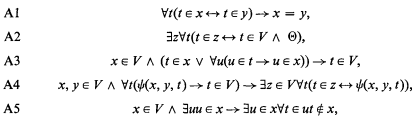
where all the free variables are shown in A4 and z does not occur in the Θ of A2. A is the theory A* − A5.

Most of our notation is standard (for instance, α, β, γ, δ, κ, λ, ξ are variables ranging over ordinals) and, in general, we follow the notation of [7]. When x ⊆ Rα, we use Df(Rα, x) for the set of those elements of Rα which are definable in 〈Rα, ∈〉, using a first order ∈-formula and parameters from x.

We refer the reader to [7] for an outline of the results which are known about A, but we shall summarise those facts which are frequently used in this paper.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 2 , June 1975 , pp. 151 - 158
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Most of the results in this paper were included in part 1 of the author's Ph.D. thesis [4], which was presented to the University of London. Dr. John Bell is thanked for a number of helpful conversations about the topics which we consider and the Science Research Council is thanked for its financial support.

References

REFERENCES

[1]Ackermann, W., Zur Axiomatik der Mengenlehre, Mathematische Annalen, vol. 131 (1956), pp. 336–345.CrossRefGoogle Scholar
[2]Grewe, R., Natural models of Ackermann's set theory, this Journal, vol. 34 (1969), pp. 481–488.Google Scholar
[3]Lake, J., On an Ackermann-type set theory, this Journal, vol. 38 (1973), pp. 410–412.Google Scholar
[4]Lake, J., Some topics in set theory, Ph.D. Thesis, University of London, 1973.Google Scholar
[5]Mostowski, A., Constructible sets with applications, North-Holland, Amsterdam, 1969.Google Scholar
[6]Novak, J., A paradoxical theorem, Fundamenta Mathematicae, vol. 37 (1950), pp. 77–83.CrossRefGoogle Scholar
[7]Reinhardt, W., Ackermann's set theory equals ZF, Annals of Mathematical Logic, vol. 2 (1970), pp. 189–249.CrossRefGoogle Scholar