Hostname: page-component-6d856f89d9-72csx Total loading time: 0 Render date: 2024-07-16T07:17:50.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Implicational complexity in intuitionistic arithmetic

Published online by Cambridge University Press:  12 March 2014

Daniel Leivant
Daniel Leivant*
Affiliation:
Ohio State University, Columbus, Ohio 43210 Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Extract

In classical arithmetic a natural measure for the complexity of relations is provided by the number of quantifier alternations in an equivalent prenex normal form. However, the proof of the Prenex Normal Form Theorem uses the following intuitionistically invalid rules for permuting quantifiers with propositional constants.

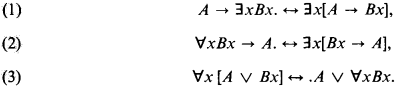
Each one of these schemas, when added to Intuitionistic (Heyting's) Arithmetic IA, generates full Classical (Peano's) Arithmetic. Schema (3) is of little interest here, since one can obtain a formula intuitionistically equivalent to A ∨ ∀xBx, which is prenex if A and B are:

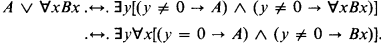
For the two conjuncts on the r.h.s. (1) may be successively applied, since y = 0 is decidable.

We shall readily verify that there is no way of similarly going around (1) or (2). This fact calls for counting implication (though not conjunction or disjunction) in measuring in IA the complexity of arithmetic relations. The natural implicational measure for our purpose is the depth of negative nestings of implication, defined as follows. I(F): = 0 if F is atomic; I(F ∧ G) = I(F ∨ G): = max[I(F), I(G)]; I(∀xF) = I(∃xF): = I(F); I(F → G):= max[I(F) + 1, I(G)].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 2 , June 1981 , pp. 240 - 248
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]de Jongh, D.H.J., Formulas of one propositional variable in intuitionistic arithmetic, Report 73–03, Department of Mathematics, University of Amsterdam, 1973.Google Scholar
[2]Kreisel, G., Schoenfield, J. and Wang, H., Number theoretic concepts and recursive well-orderings, Archiv für Mathematische Logik und Grundlugenforschung, vol. 5 (1960), pp. 42–64.CrossRefGoogle Scholar
[3]Leivant, D., Strong normalization for arithmetic, Proof theory (Diller, and Müller, , Editors), Proceedings of the 1974 European Meeting of the Association for Symbolic Logic, Kiel, Lecture Notes in Mathematics, vol. 500, Springer-Verlag, Berlin and New York, 1975, pp. 182–197.Google Scholar
[4]Leivant, D., Absoluteness of intuitionistic logic, Ph.D. dissertation, University of Amsterdam, 1975. Corrected reprint, Mathematical Centre Tract, no. 73, Amsterdam, 1979.Google Scholar
[5]Leivant, D., Maximality of logical calculi (to appear).Google Scholar
[6]Nishimura, I., On formulas of one variable in intuitionistic propositional calculus, this Journal, vol. 25 (1960), pp. 327–331.Google Scholar
[7]Troelstra, A.S., Metamathematical investigations of intuitionistic arithmetic and analysis, Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin and New York, 1973.Google Scholar
[8]Kreisel, G. and Wang, H., Some applications of formalized consistency proof, Fundamenta Mathematicae, vol. 42 (1955), pp. 101–110.CrossRefGoogle Scholar