Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-05T23:34:08.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Decidable regularly closed fields of algebraic numbers

Published online by Cambridge University Press:  12 March 2014

Lou van den Dries  and
Rick L. Smith
Lou van den Dries
Affiliation:
Department of Mathematics, Stanford UniversityStanford, California 94305
Rick L. Smith
Affiliation:
Department of Mathematics, University of Florida, Gainesville, Florida 32611
Get access Rights & Permissions [Opens in a new window]

Extract

A field K is regularly closed if every absolutely irreducible affine variety defined over K has K-rational points. This notion was first isolated by Ax [A] in his work on the elementary theory of finite fields. Later Jarden [J2] and Jarden and Kiehne [JK] extended this in different directions. One of the primary results in this area is that the elementary properties of a regularly closed field K with a free Galois group (on either finitely or countably many generators) are determined by the set of integer polynomials in one indeterminate with a zero in K. The method of proof employed in [J1], [J2] and [JK] is unusual for algebra since it is a measure-theoretic argument. In this brief summary we have not made any attempt at completeness. We refer the reader to the recent paper of Cherlin, van den Dries, and Macintyre [CDM] and to the forthcoming book by Fried and Jarden [FJ] for a more thorough discussion of the latest results. We would like to thank Moshe Jarden, Angus Macintyre, and Zoe Chatzidakis for their comments on an earlier version of this paper.

A countable field K is ω-free if the absolute Galois group 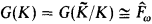, where 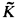is the algebraic closure of K and 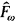is the free profinite group on ℵ0 generators.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 2 , June 1985 , pp. 468 - 475
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A]Ax, J., The elementary theory of finite fields, Annals of Mathematics, ser. 2, vol. 88 (1968), pp. 239–271.CrossRefGoogle Scholar
[CDM]Cherlin, G., van den Dries, L. and Macintyre, A., The elementary theory of regularly closed fields, Journal für die Reine und Angewandte Mathematik (to appear).Google Scholar
[D]VAn den Dries, L., New decidable fields of algebraic numbers, Proceedings of the American Mathematical Society, vol. 77 (1979), pp. 251–256.CrossRefGoogle Scholar
[FJ]Fried, M. and Jarden, M., Field arithmetic (to appear).Google Scholar
[I]Iwasawa, K., On solvable extensions of algebraic number fields, Annals of Mathematics, ser. 2, vol. 58 (1953), pp. 548–572.CrossRefGoogle Scholar
[J1]Jarden, M., Elementary statements over large algebraic fields, Transactions of the American Mathematical Society, vol. 164 (1972), pp. 67–91.CrossRefGoogle Scholar
[J2]Jarden, M., The elementary theory of ω-free Ax fields, Inventiones Mathematicae, vol. 38 (1976), pp. 181–206.CrossRefGoogle Scholar
[J3]Jarden, M., An analogue of the Čebotarev density theorem for fields of finite corank, Journal of Mathematics of Kyoto University, vol. 20 (1980), pp. 141–147.Google Scholar
[J4]Jarden, M., Algebraic extensions of finite corank of Hilbertian fields, Israel Journal of Mathematics, vol. 18 (1974), pp. 279–307.CrossRefGoogle Scholar
[JK]Jarden, M. and Kiehne, U., The elementary theory of algebraic fields of finite corank, Inventiones Mathematicae, vol. 30 (1975), pp. 275–294.CrossRefGoogle Scholar
[K]Kyuk, W., Generic approach to the Galois embedding and extension problem, Journal of Algebra, vol. 9 (1968), pp. 393–407.CrossRefGoogle Scholar
[L]Laroche, P., Effective Galois theory, this Journal, vol. 46 (1981), pp. 385–392.Google Scholar
[R]Rabin, M., Computable algebra: general theory and theory of computable fields, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[Ro]Robinson, A., Metamathematical problems, this Journal, vol. 38 (1973), pp. 500–516.Google Scholar
[W]van der Waerden, B. L., Modern algebra. Vol. 1, Ungar, New York, 1953.Google Scholar