Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-14T21:54:09.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuum cardinals generalized to Boolean algebras

Published online by Cambridge University Press:  12 March 2014

J. Donald Monk
J. Donald Monk*
Affiliation:
Department of Mathematics, 395 UCB, University of Colorado, Boulder, Colorado 80303-0395, USA, E-Mail: Don.Monk@colorado.edu
Get access Rights & Permissions [Opens in a new window]

Extract

A number of specific cardinal numbers have been defined in terms of 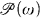/fin or ωω. Some have been generalized to higher cardinals, and some even to arbitrary Boolean algebras. Here we study eight of these cardinals, defining their generalizations to higher cardinals, and then defining them for Boolean algebras. We then attempt to completely describe their relationships within each of several important classes of Boolean algebras.

The generalizations to higher cardinals might involve several cardinals instead of just one as in the case of ω, For example, the number a associated with maximal almost disjoint families of infinite sets of integers can be generalized to talk about maximal subsets of [κ]μ subject to the pairwise intersections having size less than ν. (For this multiple generalization of 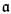. see Monk [2001].) For brevity we do not consider such generalizations, restricting ourselves to just one cardinal. The set-theoretic generalizations then associate with each infinite cardinal κ some other cardinal λ, defined as the minimum of cardinals with a certain property.

The generalizations to Boolean algebras assign to each Boolean algebra some cardinal λ, also defined as the minimum of cardinals with a certain property.

For the theory of the original “continuum” cardinal numbers, see Douwen [1984]. Balcar and Simon [1989]. and Vaughan [1990].

I am grateful to Mati Rubin for some conversations concerning these functions for superatomic algebras, and to Bohuslav Balcar for information concerning the function h.

The notation for set theory is standard. For Boolean algebras we follow Koppelberg [1989], but recall at the appropriate place any somewhat unusual notation.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 4 , December 2001 , pp. 1928 - 1958
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balcar, B. and Simon, P. [1989], Disjoint refinement, Handbook of Boolean algebras, vol. 2, North-Holland, pp. 335–386.Google Scholar
Balcar, B. and Simon, P. [1992], Reaping number and π-character of Boolean algebras, Discrete Mathematics, vol. 108, pp. 5–12.CrossRefGoogle Scholar
Baumgartner, J. [1976], Almost-disjoint sets, the dense set problem and the partition calculus, Annals of Mathematical Logic, vol. 10, pp. 401–439.CrossRefGoogle Scholar
Blass, A. and Shelah, S. [1987], There may be simple - and -points and the Rudin-Keisler ordering may be downward directed, Annals of Pure and Applied Logic, vol. 33, pp. 213–243.CrossRefGoogle Scholar
Bozeman, K. [1991], On the relationship between density and weak density in Boolean algebra, Proceedings of the American Mathematical Society, vol. 112, no. 4, pp. 1137–1141.CrossRefGoogle Scholar
Dordal, P. [1987], A model in which the base-matrix tree cannot have cofinal branches, this Journal, vol. 52, no. 3, pp. 651–664.Google Scholar
Dow, A. [1989]. Tree π-bases for βN – N in various models, Topology and its Applications, vol. 33, pp. 3–19.CrossRefGoogle Scholar
Koppelberg, S. [1989], General theory of Boolean algebras, Handbook of Boolean algebras (Monk, J.D. and Bonnet, R., editors), vol. 1, North-Holland, p. 312.Google Scholar
Kunen, K. [1980], Set theory, North-Holland.Google Scholar
Milner, E. C. and Prikry, K. [1987], Almost disjoint sets, Surveys in combinatorics, London Mathematical Society Lecture Notes Series, vol. 123, pp. 157–172.Google Scholar
Monk, J. D. [1996], Cardinal invariants on Boolean algebras, Birkhäuser Verlag.CrossRefGoogle Scholar
Monk, J. D. [1997], On minimal-sized infinite partitions of Boolean algebras, Mathematical Logic Quarterly, vol. 42, no. 4, pp. 537–550.CrossRefGoogle Scholar
Monk, J. D. [2001], The spectrum of partitions of a Boolean algebra, Archive for Mathematical Logic, to appear.CrossRefGoogle Scholar
Peterson, D. [1998], Reaping numbers and operations on Boolean algebras, Algebra Universalis, vol. 38, no. 3–4, pp. 103–119.CrossRefGoogle Scholar
Price, R. [1982], On a problem of Čech, Topology and its Applications, vol. 14, pp. 319–331.CrossRefGoogle Scholar
Shelah, S. [1984], On cardinal invariants of the continuum, Axiomatic set theory, Contemporary Mathematics, vol. 31, American Mathematical Society, pp. 183–207.CrossRefGoogle Scholar
Shelah, S. [1990], Remarks on some cardinal invariants of the continuum, Open problems in topology, North-Holland, pp. 217–218.Google Scholar
Shelah, S. [1992], CON(u > i).. Archive for Mathematical Logic, pp. 433–443.Google Scholar
Shelah, S. [2001], Are and your cup of tea?, Publication no. 700.Google Scholar
van Douwen, E. K. [1984], The integers and topology, Handbook of set-theoretic topology, North-Holland, pp. 111–167.CrossRefGoogle Scholar
Vaughan, J. E. [1990], Small uncountable cardinals and topology, Open problems in topology, North-Holland, pp. 195–218.Google Scholar
Zapletal, J. [1997], Splitting numbers at uncountable cardinals, this Journal, vol. 62, pp. 35–42.Google Scholar