Throughout this paper 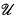denotes a nonprincipal ultrafilter and ℐ denotes the dual ideal. ℙ(ℐ) is the poset of all partial functions p: ω → 2 such that dom(p) ∈ ℐ. In [2], Grigorieff proved that ω1 is preserved in the corresponding generic extension if and only if 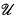is a P-point. Later, when Shelah introduced the notion of a proper poset, many people observed that if 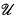is a P-point, then ℙ(ℐ) is proper. One way of proving this is to show that player II has a winning strategy in the game 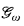for ℙ(ℐ) (see [3, p. 91].)

The notion of an Axiom A poset was introduced by Baumgartner [1]. If a poset satisfies Axiom A, then player II has a winning strategy in the game 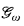for ℙ, and thus, ℙ is proper. Indeed most of the naturally occurring proper posets satisfy Axiom A (e.g., Mathias's poset and Laver's poset). Thus, it is natural to ask whether or not ℙ(ℐ) satisfies Axiom A. The main result of this paper is a negative answer to this question. We will prove this by introducing another game 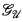and showing that 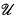is a P-point if and only if the corresponding game 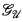is undetermined. We will then show that if ℙ(ℐ) satisfied Axiom A, then player II would have a winning strategy in the corresponding game .

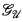We let [X]<ω = {s ⊆ X∣ ∣s∣ < ω}. We let Seq(X) denote the set of finite sequences of elements of X. If s = 〈x0, …, xn〉 ∈ Seq(X) and y ∈ X, then s * 〈y〉 = 〈x0,…,xn,y〉 ∈ Seq(X).