Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-27T21:48:55.758Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed maximality principles: implications, separations and combinations

Published online by Cambridge University Press:  12 March 2014

Gunter Fuchs
Gunter Fuchs*
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, Westfälische Wilhelms-, Universität Münster, Einsteinstr. 62, 48149 Munster, Germany, E-mail: gfuchs@math.uni-muenster.de
Get access Rights & Permissions [Opens in a new window]

Abstract

I investigate versions of the Maximality Principles for the classes of forcings which are <κ-closed, <κ-directed-closed, or of the form Col(κ, <λ). These principles come in many variants, depending on the parameters which are allowed, I shall write MPΓ (A) for the maximality principle for forcings in Γ, with parameters from A. The main results of this paper are:

• The principles have many consequences, such as <κ-closed-generic 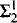(Hκ) absoluteness, and imply, e.g., that ◊κ holds. I give an application to the automorphism tower problem, showing that there are Souslin trees which are able to realize any equivalence relation, and hence that there are groups whose automorphism tower is highly sensitive to forcing.

• The principles can be separated into a hierarchy which is strict, for many κ.

• Some of the principles can be combined, in the sense that they can hold at many different κ simultaneously.

The possibilities of combining the principles are limited, though: While it is consistent that MP<κ-closed(Hκ +) holds at all regular κ below any fixed α, the “global” maximality principle, stating that MP<κ-closed (Hκ ∪ {κ} ) holds at every regular κ, is inconsistent. In contrast to this, it is equiconsistent with ZFC that the maximality principle for directed-closed forcings without any parameters holds at every regular cardinal. It is also consistent that every local statement with parameters from Hκ⊦ that's provably <κ-closed-forceably necessary is true, for all regular κ.

Keywords

Forcing axiomsMaximality Principles
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 276 - 308
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AH01]After, Arthur W. and Hamkins, Joel David, Indestructible weakly compact cardinals and the necessity of supercompactness for certain proof schemata, Mathematical Logic Quarterly, vol. 47 (2001), no. 4, pp. 563–571.Google Scholar
[ChaOO]Chalons, Christophe, Full set theory, electronic preprint, 2000.Google Scholar
[DJ74]Devlin, Keith J. and Johnsbråten, Håvard, The Souslin problem, Lecture Notes in Mathematics, vol. 405, Springer, Berlin, 1974.CrossRefGoogle Scholar
[FK03]Foreman, Matthew and Komjath, Peter, The club guessing ideal (remarks on a paper by Gitik and Shelah), 2003.Google Scholar
[FH06]Fuchs, Gunter and Hamkins, Joel David, Degrees of rigidity for Souslin trees, ArXiv Mathematics eprints, February 2006, 33 pages. Submitted to this Journal.Google Scholar
[FH07]Fuchs, Gunter, Changing the heights of automorphism towers by forcing with Souslin trees over L, ArXiv Mathematics eprints, February 2007, 23 pages. Submitted to this Journal.Google Scholar
[Ham03a]Hamkins, Joel David, Extensions with the approximation and cover properties have no new large cardinals, Fundamenta Mathematical, vol. 180 (2003), no. 3, pp. 257–277.CrossRefGoogle Scholar
[Ham03b]Hamkins, Joel David, A simple maximality principle, this Journal, vol. 68 (2003), no. 2, pp. 527–550.Google Scholar
[HT00]Hamkins, Joel David and Thomas, Simon, Changing the heights of automorphism towers, Annals of Pure and Applied Logic, vol. 102 (2000), no. 1-2, pp. 139–157.CrossRefGoogle Scholar
[HW05]Hamkins, Joel David and Hughwoodin, W., The necessary maximality principle for c.c.c.forcing is equiconsistent with a weakly compact cardinal, Mathematical Logic Quarterly, vol. 51 (2005), no. 5, pp. 493–498.CrossRefGoogle Scholar
[Jec03]Jech, Thomas, Set theory, The Third Millenium ed., Springer, Berlin, 2003.Google Scholar
[JSSS07]Jensen, Ronald B., Schimmerlino, Ernest, Schindler, Ralf, and Steel, John R., Stacking mice, in preparation, 2007.Google Scholar
[KY06]König, Bernhard and Yoshinobu, Yasuo, Kurepa-trees and Namba forcing, ArXiv Mathematics eprints, http://arXiv.org/pdf/math/0605130, 05 2006.Google Scholar
[Kun80]Kunen, Kenneth, Set theory. An introduction to independence proofs, North Holland, 1980.Google Scholar
[Lav78]Laver, Richard, Making the supercompactness of κ indestructible under κ-directed closed forcing, Israel Journal of Mathematics, vol. 29 (1978), no. 4, pp. 385–388.CrossRefGoogle Scholar
[Lei04]Leibman, George, Consistency strengths of modified maximality principles, Ph.D. thesis, The City University of New York, 2004.Google Scholar
[Rei06]Reitz, Jonas, The ground axiom, Ph.D. thesis, CUNY Graduate Center, 2006.Google Scholar
[SS99]Schimmerling, Ernest and Steel, John R., The maximality of the core model, Transactions of the American Mathematical Society, vol. 351 (1999), no. 8, pp. 3119–3141.CrossRefGoogle Scholar
[SVOl]Stavi, Jonathan and Väänanen, Jouko, Reflection principles for the continuum, Logic and algebra, Contemporary Mathematics Series, vol. 302, AMS, 2001, pp. 59–84.CrossRefGoogle Scholar
[Tho]Thomas, Simon, The automorphism tower problem, to appear.Google Scholar