Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-01T01:46:48.706Z Has data issue: false hasContentIssue false
  • English
  • Français

An analogue of Hilbert's tenth problem for p-adic entire functions

Published online by Cambridge University Press:  12 March 2014

Leonard Lipshitz  and
Thanases Pheidas
Leonard Lipshitz
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, Indiana 47907, E-mail: lipshitz@math.purdue.edu
Thanases Pheidas
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801 Department of Mathematics, University of Crete, 71409 Herakleio, Crete, Greece, E-mail: pheidas@talos.cc.uch.gr
Get access Rights & Permissions [Opens in a new window]

Extract

Let p be a fixed prime integer, other than 2, Qp the field of p-adic numbers, and Ωp the completion of the algebraic closure of Qp. Let Rp be the ring of entire functions in one variable t over Ωp; that is, Rp is the ring of functions f: Ωp → Qp such that f(t) is given by a power series around 0, of infinite radius of convergence:

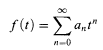
and 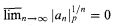where ∣a∣p is the p-adic norm of a in Ωp. We prove:

Theorem A. The positive existential theory of Rp in the language L = {0, 1, t, +, ·} is undecidable.

Theorem A gives a negative answer to the analogue of Hilbert's tenth problem for Rp in the language L. Related results include those of [2] where it is shown that the first-order theory of entire functions on the complex plane is undecidable and the similar result for analytic functions on the open unit disk (this is due to Denef and Gromov, communicated to us by Cherlin and is as of now unpublished).

It would be desirable to have a similar result in the language which, instead of the variable t, has a predicate for the transcendental (that is, nonconstant) elements of Rp. A related problem is the similar problem for meromorphic functions on the real or p-adic plane or on the unit open or closed disk. These problems seem for the moment rather hard in view of the fact that the analogue of Hilbert's Tenth Problem for the field of rational functions over the complex numbers (or any algebraically closed field of characteristic zero) is an open problem.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 4 , December 1995 , pp. 1301 - 1309
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Bosch, S., Güntzer, U., and Remmert, R., Non-Archimedean analysis, Comprehensive Studies in Mathematics, vol. 261, Springer-Verlag, 1984.CrossRefGoogle Scholar
[2]Denef, J., The Diophantine problem for polynomial rings and fields of rational functions, Transactions of the American Mathematical Society, vol. 242 (1978), pp. 391–399.CrossRefGoogle Scholar
[3]Koblitz, N., p-adic numbers, p-adic analysis and zeta-functions, 2nd ed., Springer-Verlag, 1984.CrossRefGoogle Scholar
[4]Matiyasevich, Y., Enumerable sets are diophantine, Doklady Akademti Nauk SSSR, vol. 191 (1970), pp. 272–282.Google Scholar