Article contents
Truth definitions without exponentiation and the Σ1 collection scheme
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that:
• if there is a model of IΔ0 + ¬exp with cofinal Σ1-definable elements and a Σ1 truth definition for Σ1 sentences, then IΔ0 + ¬exp + ¬BΣ1 is consistent,
• there is a model of IΔ0 + Ω1 + ¬exp with cofinal Σ1-definable elements, both a Σ2 and a Π2 truth definition for Σ1 sentences, and for each n ≥ 2, a Σn truth definition for Σn sentences.
The latter result is obtained by constructing a model with a recursive truth-preserving translation of Σ1 sentences into boolean combinations of 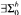 sentences.
sentences.
We also present an old but previously unpublished proof of the consistency of IΔ0 + ¬exp + ¬BΣ1 under the assumption that the size parameter in Lessan's Δ0 universal formula is optimal. We then discuss a possible reason why proving the consistency of IΔ0 + ¬exp + ¬BΣ1 unconditionally has turned out to be so difficult.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012
References
REFERENCES
- 2
- Cited by




