No CrossRef data available.
Article contents
SOME CONSEQUENCES OF  ${\mathrm {TD}}$ AND
${\mathrm {TD}}$ AND 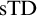 ${\mathrm {sTD}}$
${\mathrm {sTD}}$
Published online by Cambridge University Press: 15 May 2023
Abstract
Strong Turing Determinacy, or  ${\mathrm {sTD}}$, is the statement that for every set A of reals, if
${\mathrm {sTD}}$, is the statement that for every set A of reals, if 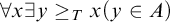 $\forall x\exists y\geq _T x (y\in A)$, then there is a pointed set
$\forall x\exists y\geq _T x (y\in A)$, then there is a pointed set 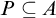 $P\subseteq A$. We prove the following consequences of Turing Determinacy (
$P\subseteq A$. We prove the following consequences of Turing Determinacy ( ${\mathrm {TD}}$) and
${\mathrm {TD}}$) and  ${\mathrm {sTD}}$ over
${\mathrm {sTD}}$ over 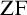 ${\mathrm {ZF}}$—the Zermelo–Fraenkel axiomatic set theory without the Axiom of Choice:
${\mathrm {ZF}}$—the Zermelo–Fraenkel axiomatic set theory without the Axiom of Choice:
(1)
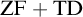 ${\mathrm {ZF}}+{\mathrm {TD}}$ implies
${\mathrm {ZF}}+{\mathrm {TD}}$ implies 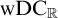 $\mathrm {wDC}_{\mathbb {R}}$—a weaker version of
$\mathrm {wDC}_{\mathbb {R}}$—a weaker version of 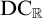 $\mathrm {DC}_{\mathbb {R}}$.
$\mathrm {DC}_{\mathbb {R}}$.(2)
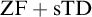 ${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every set of reals is measurable and has Baire property.
${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every set of reals is measurable and has Baire property.(3)
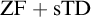 ${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every uncountable set of reals has a perfect subset.
${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that every uncountable set of reals has a perfect subset.(4)
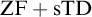 ${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that for every set of reals A and every
${\mathrm {ZF}}+{\mathrm {sTD}}$ implies that for every set of reals A and every 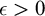 $\epsilon>0$:
$\epsilon>0$:(a) There is a closed set
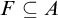 $F\subseteq A$ such that
$F\subseteq A$ such that 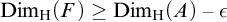 $\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)-\epsilon $, where
$\mathrm {Dim_H}(F)\geq \mathrm {Dim_H}(A)-\epsilon $, where 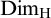 $\mathrm {Dim_H}$ is the Hausdorff dimension.
$\mathrm {Dim_H}$ is the Hausdorff dimension.(b) There is a closed set
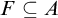 $F\subseteq A$ such that
$F\subseteq A$ such that 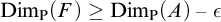 $\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)-\epsilon $, where
$\mathrm {Dim_P}(F)\geq \mathrm {Dim_P}(A)-\epsilon $, where 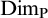 $\mathrm {Dim_P}$ is the packing dimension.
$\mathrm {Dim_P}$ is the packing dimension.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic





