Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-5c569c448b-r8t2r Total loading time: 0.21 Render date: 2022-07-03T10:02:18.612Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true } hasContentIssue true
  • English
The Journal of Symbolic Logic The Journal of Symbolic Logic

Article contents

Random reals and possibly infinite computations Part I: Randomness in ∅′

Published online by Cambridge University Press:  12 March 2014

Verónica Becher  and
Serge Grigorieff
Verónica Becher
Affiliation:
Departamento de Computación, Fceyn Universidad de Buenos Aires, ArgentinaE-mail:, vbecher@dc.uba.ar
Serge Grigorieff
Affiliation:
Liafa, Université Paris7, 2, Pl. Jussieu 75251 Paris Cedex 05, FranceE-mail:, seg@liafa.jussieu.fr
Get access Rights & Permissions[Opens in a new window]

Abstract

Using possibly infinite computations on universal monotone Turing machines, we prove Martin-Löf randomness in ∅′ of the probability that the output be in some set 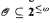under complexity assumptions about .

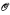Type
Research Article
Information
The Journal of Symbolic Logic , Volume 70 , Issue 3 , September 2005 , pp. 891 - 913
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Becher, V. and Chaitin, G., Another example of higher order randomness, Fundamenta Informaticae, vol. 51 (2002), no. 4, pp. 325–338.Google Scholar
[2]Becher, V., Chaitin, G., and Daicz, S., A highly random number, Proceedings of the third discrete mathematics and theoretical computer science conference (DMTCS '01) (Calude, C. S., Dineen, M. J., and Sburlan, S., editors), Springer-Verlag, 2001, pp. 55–68.Google Scholar
[3]Becher, V. and Grioorieff, S., Recursion and topology on 2≤ω-m for possibly infinite computations, Theoretical Computer Science, vol. 322 (2004), pp. 85–136.CrossRefGoogle Scholar
[4]Becher, V., Random reals and possibly infinite computations, Part II: Higher order randomness, In preparation.Google Scholar
[5]Becher, V., Wadge reducibility and spectral continuous maps into 2≤ω, In preparation.Google Scholar
[6]Boasson, L. and Nivat, M., Adherences of languages, Journal of Computer and System Sciences, vol. 20 (1980), pp. 285–309.CrossRefGoogle Scholar
[7]Calude, C., Information and randomness, Springer, 1994.CrossRefGoogle Scholar
[8]Calude, C. S., Hertling, P. H., and Khoussainov, B.Wang, Y., Recursively enumerable reals and Chaitin Ω numbers, STACS 98 (Paris, 1998), Lecture Notes in Computer Science, no. 1373, Springer-Verlag, 1998, pp. 596–606.CrossRefGoogle Scholar
[9]Chaitin, G., A theory of program size formally identical to information theory, Journal of the ACM, vol. 22 (1975), pp. 329–340, Available on Chaitin's home page.CrossRefGoogle Scholar
[10]Chaitin, G., Algorithmic entropy of sets, Computers & Mathematics with Applications, vol. 2 (1976), pp. 233–245. Available on Chaitin's home page.CrossRefGoogle Scholar
[11]Chaitin, G., Algorithmic information theory, 1st ed., Cambridge University Press, 1987.CrossRefGoogle Scholar
[12]Downey, R., Some computability-theoretical aspects of reals and randomness, Notes from lectures given at the University Notre Dame. Available at MSCS, University of Wellington, NZ, 2000.Google Scholar
[13]Downey, R. and Hirschfeldt, D., Algorithmic randomness and complexity, Springer, 2005, To appear. Preliminary version, November 30th 2004, available on Downey's home page.Google Scholar
[14]Downey, R., Hirschfeldt, D., and Nies, A., Randomness, computability and density, SIAM Journal on Computing, vol. 31 (2002), pp. 1169–1183, Extended abstract in Proceedings of the STACS 2001, LNCS 2010.CrossRefGoogle Scholar
[15]Downey, R. and Laforte, G. L., Presentations of computably enumerable reals, Theoretical Computer Science, vol. 284 (2002), no. 2, pp. 539–555.CrossRefGoogle Scholar
[16]Head, T., The adherences of languages as topological spaces, Automata andinfinite words (Nivat, M. and Perrin, D., editors), Lecture Notes in Computer Science, vol. 192, 1985, pp. 147–163.CrossRefGoogle Scholar
[17]Head, T., The topological structure of adherence of regular languages, RAIRO, Theoretical Informatics and Applications, vol. 20 (1986), pp. 31–41.CrossRefGoogle Scholar
[18]Kechris, A. S., Classical descriptive set theory, Springer, 1995.CrossRefGoogle Scholar
[19]Levin, L., On the notion of random sequence, Soviet Math. Dokl., vol. 14 (1973), no. 5, pp. 1413–1416.Google Scholar
[20]Li, M. and Vitanyi, P., An introduction to Kolmogorov complexity and its applications, 2d ed., Springer, 1997.CrossRefGoogle Scholar
[21]Martin-Löf, P., The definition of random sequences, Information and Control, vol. 9 (1966), pp. 602–619.CrossRefGoogle Scholar
[22]Miller, J., Personal communication.Google Scholar
[23]Moschovakis, Y. N., Descriptive set theory, North Holland, 1980.Google Scholar
[24]Muchnik, An. A., Personal communication.Google Scholar
[25]Odifreddi, P., Classical recursion theory, Studies in Logic, vol. 125, North-Holland, 1989.Google Scholar
[26]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, 1967.Google Scholar
[27]Sacks, G. E., Degrees of unsolvahility, Annals of mathematical studies, Princeton University Press, 1966.Google Scholar
[28]Schnorr, C. P., Process complexity and effective random tests, Journal of Computer and System Sciences, vol. 7 (1973), pp. 376–388.CrossRefGoogle Scholar
[29]Schnorr, C. P., A survey of the theory of random sequences, Basic problems in methodology and linguistics (Butts, R. E. and Hintikka, J., editors), D. Reidel, 1977, pp. 193–210.CrossRefGoogle Scholar
[30]Soare, R., Recursion theory and Dedekind cuts, Transactions of the American Mathematical Society, vol. 140 (1969), pp. 271–294.Google Scholar
[31]Solovay, R. M., Draft of a paper (or a series of papers) on Chaitin's work, Unpublished manuscript, IBM Research Center, NY, 1975.Google Scholar
[32]Solovay, R. M., On random R.E. sets, Non-classical logics, model theory and computability (Arruda, A. I., da Costa, N. C. A., and Chuaqui, R., editors), North-Holland, 1977, pp. 283–307.CrossRefGoogle Scholar
[33]Turing, A., On computable numbers, with an application to the Entscheidungsproblem., Proceedings of the London Mathematical Society, 2nd series, vol. 42 (1936), pp. 230–265. Correction, A. Turing, On computable numbers, with an application to the Entscheidungsproblem., Proceedings of the London Mathematical Society, 2nd series, vol. 43 (1937) pp. 544–546.Google Scholar
[34]Wadge, W. W., Degrees of complexity of subsets of the Baire space, Notices of the American Mathematical Society, (1972), pp. A–714.Google Scholar
[35]Wadge, W. W., Degrees of complexity of subsets of the Baire space, Ph.D. thesis, University of Berkeley, 1984.Google Scholar
12
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Random reals and possibly infinite computations Part I: Randomness in ∅′
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Random reals and possibly infinite computations Part I: Randomness in ∅′
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Random reals and possibly infinite computations Part I: Randomness in ∅′
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *