No CrossRef data available.
Article contents
Partitioning large vector spaces
Published online by Cambridge University Press: 12 March 2014
Extract
The theme of this paper is the generalization of theorems about partitions of the sets of points and lines of finite-dimensional Euclidean spaces ℝd to vector spaces over ℝ of arbitrary dimension and, more generally still, to arbitrary vector spaces over other fields so long as these fields are not too big. These theorems have their origins in the following striking theorem of Sierpiński [12] which appeared a half century ago.
Sierpiński's Theorem. The Continuum Hypothesis is equivalent to: There is a partition {X, Y, Z} of ℝ3such that if ℓ is a line parallel to the x-axis [respectively: y-axis, z-axis] then X ∩ ℓ [respectively: Y ∩ ℓ, Z ∩ ℓ] is finite.
The history of this theorem and some of its subsequent developments are discussed in the very interesting article by Simms [13]. Sierpiński's Theorem was generalized by Kuratowski [9] to partitions of ℝn+2 into n + 2 sets obtaining an equivalence with 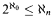 . The geometric character that Sierpiński's Theorem and its generalization by Kuratowski appear to have is bogus, since the lines parallel to coordinate axes are essentially combinatorial, rather than geometric, objects. The following version of Kuratowski's theorem emphasizes its combinatorial character.
. The geometric character that Sierpiński's Theorem and its generalization by Kuratowski appear to have is bogus, since the lines parallel to coordinate axes are essentially combinatorial, rather than geometric, objects. The following version of Kuratowski's theorem emphasizes its combinatorial character.
Kuratowski's Theorem. Let n < ω and A be any set. Then ∣A∣ ≤ ℵnif and only if there is a partition P: An+2 → n + 2 such that if i ≤ n + 1 and ℓ is a line parallel to the i-th coordinate axis, then {x ∈ ℓ: P(x) = i} is finite.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2003




