Article contents
From index sets to randomness in ∅n: random reals and possibly infinite computations part II
Published online by Cambridge University Press: 12 March 2014
Abstract
We obtain a large class of significant examples of n-random reals (i.e., Martin-Löf random in oracle ∅(n−1)) à la Chaitin. Any such real is defined as the probability that a universal monotone Turing machine performing possibly infinite computations on infinite (resp. finite large enough, resp. finite self-delimited) inputs produces an output in a given set 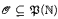 . In particular, we develop methods to transfer
. In particular, we develop methods to transfer 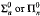 many-one completeness results of index sets to n-randomness of associated probabilities.
many-one completeness results of index sets to n-randomness of associated probabilities.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2009
References
REFERENCES
- 9
- Cited by




