Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Downey, Rod
2004.
Mathematical Foundations of Computer Science 2004.
Vol. 3153,
Issue. ,
p.
42.
Mileti, Joseph R.
2005.
Partition Theorems and Computability Theory.
Bulletin of Symbolic Logic,
Vol. 11,
Issue. 3,
p.
411.
Dzhafarov, Damir D.
and
Hirst, Jeffry L.
2009.
The polarized Ramsey’s theorem.
Archive for Mathematical Logic,
Vol. 48,
Issue. 2,
p.
141.
Shore, Richard A.
2010.
Reverse Mathematics: The Playground of Logic.
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 3,
p.
378.
Dzhafarov, Damir D.
2011.
Stable Ramsey's Theorem and Measure.
Notre Dame Journal of Formal Logic,
Vol. 52,
Issue. 1,
Kreuzer, Alexander P.
2012.
Primitive Recursion and the Chain Antichain Principle.
Notre Dame Journal of Formal Logic,
Vol. 53,
Issue. 2,
Corduan, Jared R.
and
Dorais, François G.
2012.
On the Indecomposability of ωn.
Notre Dame Journal of Formal Logic,
Vol. 53,
Issue. 3,
Kjos-Hanssen, Bjørn
Stephan, Frank
and
Terwijn, Sebastiaan A.
2015.
Evolving Computability.
Vol. 9136,
Issue. ,
p.
44.
Patey, Ludovic
2015.
Degrees bounding principles and universal instances in reverse mathematics.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 11,
p.
1165.
PATEY, LUDOVIC
2016.
OPEN QUESTIONS ABOUT RAMSEY-TYPE STATEMENTS IN REVERSE MATHEMATICS.
The Bulletin of Symbolic Logic,
Vol. 22,
Issue. 2,
p.
151.
Solomon, Reed
2016.
Pursuit of the Universal.
Vol. 9709,
Issue. ,
p.
182.
Hirschfeldt, Denis R.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
22.
Kjos-Hanssen, Bjørn
Stephan, Frank
and
Terwijn, Sebastiaan A.
2017.
Covering the recursive sets.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 4,
p.
804.
Patey, Ludovic
and
Yokoyama, Keita
2018.
The proof-theoretic strength of Ramsey's theorem for pairs and two colors.
Advances in Mathematics,
Vol. 330,
Issue. ,
p.
1034.
Monin, Benoit
and
Patey, Ludovic
2019.
Pigeons do not jump high.
Advances in Mathematics,
Vol. 352,
Issue. ,
p.
1066.
Cholak, Peter A.
Dzhafarov, Damir D.
Hirschfeldt, Denis R.
Patey, Ludovic
Brattka, Vasco
Dzhafarov, Damir D.
Marcone, Alberto
and
Pauly, Arno
2020.
Some results concerning the SRT 2 2 vs. COH problem.
Computability,
Vol. 9,
Issue. 3-4,
p.
193.
Monin, Benoit
and
Patey, Ludovic
2021.
SRT22 does not imply RT22 in ω-models.
Advances in Mathematics,
Vol. 389,
Issue. ,
p.
107903.
Benham, Heidi
DeLapo, Andrew
Dzhafarov, Damir D.
Solomon, Reed
and
Villano, Java Darleen
2024.
The Ginsburg–Sands theorem and computability theory.
Advances in Mathematics,
Vol. 444,
Issue. ,
p.
109618.
MONIN, BENOIT
and
PATEY, LUDOVIC
2024.
PARTITION GENERICITY AND PIGEONHOLE BASIS THEOREMS.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
829.


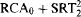 must contain a nonlow set.
must contain a nonlow set.