Research Article
Hybrid logics: characterization, interpolation and complexity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 977-1010
-
- Article
- Export citation
An axiomatization of full Computation Tree Logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1011-1057
-
- Article
- Export citation
A boundedness lemma for iterations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1058-1072
-
- Article
- Export citation
First order theories for nonmonotone inductive definitions: recursively inaccessible and Mahlo
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1073-1089
-
- Article
- Export citation
On elementary embeddings from an inner model to the universe
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1090-1116
-
- Article
- Export citation
A note on the isomorphism problem for SK[G]
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1117-1120
-
- Article
- Export citation
An intuitionistic version of Zermelo's proof that every choice set can be well-ordered
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1121-1126
-
- Article
- Export citation
Stable theories with a new predicate
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1127-1140
-
- Article
- Export citation
Canonicity for Intensional Logics with Even Axioms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1141-1156
-
- Article
- Export citation
Can partial indexings be totalized?
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1157-1185
-
- Article
- Export citation
Unfoldable cardinals and the GCH
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1186-1198
-
- Article
- Export citation
Computational randomness and lowness*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1199-1205
-
- Article
- Export citation
Existence of prime elements in rings of generalized power series
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1206-1216
-
- Article
- Export citation
Number of variables is equivalent to space
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1217-1230
-
- Article
- Export citation
Number systems with simplicity hierarchies: a generalization of Conway's theory of surreal numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1231-1258
-
- Article
- Export citation
Cofinitary groups, almost disjoint and dominating families
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1259-1276
-
- Article
- Export citation
Exact bounds for lengths of reductions in typed λ-calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1277-1285
-
- Article
- Export citation
Main gap for locally saturated elementary submodels of a homogeneous structure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1286-1302
-
- Article
- Export citation
Properties of ideals on the generalized Cantor spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1303-1320
-
- Article
- Export citation
An axiomatics for nonstandard set theory, based on von Neumann–Bernays–Gödel Theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1321-1341
-
- Article
- Export citation



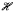 (↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that
(↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that 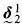 such that for some formula
such that for some formula 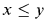
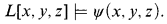
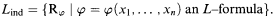
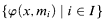
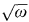 and
and 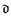 and
and 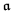 .
.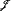 we produce a
we produce a 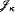 of subsets of the generalized Cantor space 2
of subsets of the generalized Cantor space 2