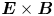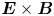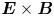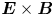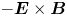1. Introduction
Low-temperature magnetised plasmas can be found in a variety of applications and natural phenomena, including magnetron discharges (Keidar & Beilis Reference Keidar and Beilis2006; Anders Reference Anders2012; Ito, Young & Cappelli Reference Ito, Young and Cappelli2015; Hecimovic & von Keudell Reference Hecimovic and von Keudell2018), Penning discharges (Quraishi, Robertson & Walch Reference Quraishi, Robertson and Walch2002; Abolmasov Reference Abolmasov2012), Hall effect thrusters (HETs) and accelerators (Ellison, Raitses & Fisch Reference Ellison, Raitses and Fisch2012; Sekerak et al. Reference Sekerak, Longmier, Gallimore, Brown, Hofer and Polk2015; Romadanov et al. Reference Romadanov, Smolyakov, Raitses, Kaganovich, Tang and Ryzhkov2016; Mazouffre et al. Reference Mazouffre, Grimaud, Tsikata, Matyash and Schneider2019), high-power microwaves (Lau Reference Lau2001; Benford, Swegle & Schamiloglu Reference Benford, Swegle and Schamiloglu2015), dusty (complex) plasmas (Bal & Bose Reference Bal and Bose2010) and interplanetary and interstellar environments (Breneman et al. Reference Breneman, Cattell, Kersten, Paradise, Schreiner, Kellogg, Goetz and Wilson2013). An applied magnetic field traps the charged particles, thus increasing ionisation efficiency and reducing the diffusivity, serving as a critical path to control flows and chemistry in low-temperature plasmas.
Depending on the magnetic field strength and collision frequency, plasmas can be either partially magnetised (i.e. electrons are magnetised but ions are non-magnetised) or fully magnetised (i.e. both ions and electrons are magnetised). In low-temperature plasmas, the dynamics of the neutral gas also play an important role in the transport properties and time-dependent plasma behaviour. The multiscale nature of the plasma flow in such low-temperature magnetised plasmas leads to various oscillation modes from high frequency (of the order of gigahertz) to low frequency (of the order of kilohertz) (Hara Reference Hara2019). Recent studies suggest that the anomalous electron transport across magnetic fields can be due to plasma–wall interaction (Kaganovich et al. Reference Kaganovich, Raitses, Sydorenko and Smolyakov2007; Sydorenko et al. Reference Sydorenko, Smolyakov, Kaganovich and Raitses2008), the plasma waves initiated by kinetic instabilities (Adam, Héron & Laval Reference Adam, Héron and Laval2004; Héron & Adam Reference Héron and Adam2013; Boeuf Reference Boeuf2017; Janhunen et al. Reference Janhunen, Smolyakov, Sydorenko, Jimenez, Kaganovich and Raitses2018) or a combination of these effects (Héron & Adam Reference Héron and Adam2013; Villafana et al. Reference Villafana, Petronio, Denig, Jimenez, Eremin, Garrigues, Taccogna, Alvarez-Laguna, Boeuf and Bourdon2021). A few examples of the kinetic instabilities in the high-frequency range include the electron cyclotron drift instability (Forslund, Morse & Nielson Reference Forslund, Morse and Nielson1971), modified two-stream instability (McBride et al. Reference McBride, Ott, Boris and Orens1972), and ion–ion two-stream instability (Gary Reference Gary1991; Tsikata et al. Reference Tsikata, Cavalier, Héron, Honoré, Lemoine, Grésillon and Coulette2014). On the other hand, low-frequency plasma oscillations include breathing mode oscillations (Boeuf & Garrigues Reference Boeuf and Garrigues1998; Barral & Ahedo Reference Barral and Ahedo2009; Hara et al. Reference Hara, Sekerak, Boyd and Gallimore2014a, Reference Hara, Sekerak, Boyd and Gallimoreb; Dale & Jorns Reference Dale and Jorns2019) and azimuthally rotating spokes (Ellison et al. Reference Ellison, Raitses and Fisch2012; Sekerak et al. Reference Sekerak, Longmier, Gallimore, Brown, Hofer and Polk2015; Kawashima, Hara & Komurasaki Reference Kawashima, Hara and Komurasaki2018). The coupling between different instabilities in various spatial and temporal scales plays an important role in determining the transport coefficients and turbulent phenomena in such low-temperature magnetised plasmas.
In this paper, we derive the dispersion relation of low-frequency, large-wavelength gradient drift instabilities, which may lead to the self-organising patterns in the low-temperature magnetised plasmas. We consider a Penning-type configuration, where a homogeneous axial magnetic field is applied and an electric field and density gradient exist in the radial direction. Although the spokes are often observed in numerical simulations (Boeuf Reference Boeuf2014; Powis et al. Reference Powis, Carlsson, Kaganovich, Raitses and Smolyakov2018; Boeuf & Takahashi Reference Boeuf and Takahashi2020) and in experiments (Raitses, Kaganovich & Smolyakov Reference Raitses, Kaganovich and Smolyakov2015; Marcovati, Ito & Cappelli Reference Marcovati, Ito and Cappelli2020), the mechanism of the spoke formation is still not well understood. One of the most accepted theories attributes the formation of rotating spokes in a Penning-type discharge to the class of Simon–Hoh instabilities (SHIs) (Simon Reference Simon1963; Hoh Reference Hoh1963). This terminology was first used by Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993), who proposed the modified Simon–Hoh instability (MSHI), which comes from a dispersion relation for partially magnetised plasma, whereas the original work by Simon and Hoh individually focused on fully magnetised plasmas. In work by Simon (Reference Simon1963), the criterion for rotating spoke formation has been proposed to be $\boldsymbol {E}_0\boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$![]() , where $\boldsymbol {E}_0$
, where $\boldsymbol {E}_0$![]() is the applied electric field and $\boldsymbol {\nabla } n_0$
is the applied electric field and $\boldsymbol {\nabla } n_0$![]() is the equilibrium plasma density gradient. Recent experimental studies in low-temperature magnetised plasma sources have shown, however, that the rotation direction and speed can depend on various plasma parameters, such as the current (Anders & Yang Reference Anders and Yang2017), indicating that the instability criterion needs to be revisited.
is the equilibrium plasma density gradient. Recent experimental studies in low-temperature magnetised plasma sources have shown, however, that the rotation direction and speed can depend on various plasma parameters, such as the current (Anders & Yang Reference Anders and Yang2017), indicating that the instability criterion needs to be revisited.
The theory of gradient-drift instabilities in low-temperature magnetised plasmas is introduced in this paper. Section 2 discusses the linearised fluid equations for magnetised plasmas under an applied magnetic field, assuming that the gyroviscosity effects are negligible. Section 3 shows a low-frequency plasma dispersion relation of the partially magnetised plasma considering a slab geometry. The criteria for the large-wavelength, low-frequency, gradient drift instability under a homogeneous magnetic field are discussed. Section 4 illustrates the results of the dispersion relation for partially magnetised plasmas, showing results consistent with the instability criteria derived in § 3. The gradient drift instability theory is applied to various cross-field plasma devices in § 5.
2. Linearised plasma equations for low-temperature magnetised plasmas
Although the rotating spokes are observed in cylindrical (axisymmetric) systems, here we simplify the dispersion relation assuming a slab (Cartesian) geometry. A static, uniform magnetic field in $z$![]() direction $\boldsymbol {B} = B_0 \hat {\boldsymbol {z}}$
direction $\boldsymbol {B} = B_0 \hat {\boldsymbol {z}}$![]() and an equilibrium electric field (applied electric field) are considered: $\boldsymbol {E}_0 = E_0 \hat {\boldsymbol {x}}$
and an equilibrium electric field (applied electric field) are considered: $\boldsymbol {E}_0 = E_0 \hat {\boldsymbol {x}}$![]() . It is assumed that the equilibrium plasma is quasineutral and a plasma density gradient exists locally in the $x$
. It is assumed that the equilibrium plasma is quasineutral and a plasma density gradient exists locally in the $x$![]() direction: $E_{0} \neq 0$
direction: $E_{0} \neq 0$![]() and ${\rm d}n_0 /{{\rm d} x} \neq 0$
and ${\rm d}n_0 /{{\rm d} x} \neq 0$![]() , generating $\boldsymbol {E}\times \boldsymbol {B}$
, generating $\boldsymbol {E}\times \boldsymbol {B}$![]() and diamagnetic drifts in the ${\pm }y$
and diamagnetic drifts in the ${\pm }y$![]() direction, for the equilibrium condition. In addition, the following assumptions are made: (i) although the temperature gradient may affect the instabilities, we assume that the temperature is uniform and constant, for simplicity; (ii) only ions and electrons are assumed for the species; (iii) the plasma is assumed to be partially magnetised (i.e. magnetised electrons and unmagnetised ions); (iv) collisions are assumed negligible; and (v) the plasma is electrostatic, that is, effects of the induced magnetic field are negligible compared with the applied magnetic field.
direction, for the equilibrium condition. In addition, the following assumptions are made: (i) although the temperature gradient may affect the instabilities, we assume that the temperature is uniform and constant, for simplicity; (ii) only ions and electrons are assumed for the species; (iii) the plasma is assumed to be partially magnetised (i.e. magnetised electrons and unmagnetised ions); (iv) collisions are assumed negligible; and (v) the plasma is electrostatic, that is, effects of the induced magnetic field are negligible compared with the applied magnetic field.
2.1. Governing equations
The fluid equations are used for both ions and electrons, i.e. when kinetic effects, such as the Bernstein modes (Bernstein Reference Bernstein1958), can be neglected.
Conservation of mass can be constructed by taking the zeroth moment of the kinetic equation. Here, ionisation and recombination are neglected. Thus, the continuity equation can be written as
where $n_s$![]() is the number density and $\boldsymbol {u}_s$
is the number density and $\boldsymbol {u}_s$![]() is the bulk velocity for species $s$
is the bulk velocity for species $s$![]() .
.
The equation for the fluid momentum can be formulated by taking the first moment of the kinetic equation, which can be written using conservative or primitive variables. Assuming that the plasma is collisionless and the distribution function is close to an isotropic Maxwellian distribution function, the conservation of momentum can be written as
where $m_s$![]() is the mass, $p_s$
is the mass, $p_s$![]() is the pressure, $q_s$
is the pressure, $q_s$![]() is the charge, $\boldsymbol {E}$
is the charge, $\boldsymbol {E}$![]() is the electric field and $\boldsymbol {B}$
is the electric field and $\boldsymbol {B}$![]() is the magnetic field. Using the source-less continuity equation, as shown in (2.1), the momentum equation can also be given, using the primitive variables, by
is the magnetic field. Using the source-less continuity equation, as shown in (2.1), the momentum equation can also be given, using the primitive variables, by
Note that the pressure is a scalar term, which is valid when the velocity distribution function (VDF) is close to an isotropic Maxwellian distribution function, that is, the temperatures in three directions are equal. Under this condition, the pressure can be written using the ideal gas law: $p_s = n_s k_B T_s$![]() , where $k_B$
, where $k_B$![]() is the Boltzmann constant and $T_s$
is the Boltzmann constant and $T_s$![]() is the temperature for species $s$
is the temperature for species $s$![]() .
.
In the present model, the ideal gas law is assumed for the electron fluid model. It is to be noted that standard drift models account for gyroviscosity effects, which arise due to the non-Maxwellian distribution and lead to cancellation of the diamagnetic drift in the inertia term in the momentum equation (Ramos Reference Ramos2005; Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006). Although the gyroviscosity effects may play an important role in low-temperature, partially magnetised plasmas (Smolyakov et al. Reference Smolyakov, Chapurin, Frias, Koshkarov, Romadanov, Tang, Umansky, Raitses, Kaganovich and Lakhin2016), the validity of the drift models and the necessity of including gyroviscosity effects in low-temperature magnetised plasmas needs to be investigated. In the state-of-the-art computational models for low-temperature plasmas, simplified fluid models such as the drift-diffusion model are known to represent the physical processes (Kushner Reference Kushner2009; Hara Reference Hara2019). In this paper, a five-moment model that neglects the gyroviscosity effects is used, based on recent numerical simulations that show low-frequency rotating spokes (Mansour & Hara Reference Mansour and Hara2022). The inclusion of the gyroviscosity effects is reserved for future work.
2.2. Linear perturbation analysis for partially magnetised plasmas
We consider the growth of the instabilities in $y$![]() direction, that is, the direction in which the electrons drift. Under the linear perturbation analysis, a plasma property $Q$
direction, that is, the direction in which the electrons drift. Under the linear perturbation analysis, a plasma property $Q$![]() can be described as a sum of the steady-state quantity and a linear perturbation, such that
can be described as a sum of the steady-state quantity and a linear perturbation, such that
where $Q_0$![]() and $Q_1$
and $Q_1$![]() are the equilibrium (steady-state) and first-order perturbation terms of a plasma property $Q$
are the equilibrium (steady-state) and first-order perturbation terms of a plasma property $Q$![]() , respectively, $\omega$
, respectively, $\omega$![]() is the frequency, $t$
is the frequency, $t$![]() is time and $k_y$
is time and $k_y$![]() is the wave number in the $y$
is the wave number in the $y$![]() direction. Here, $\omega = \omega _r + {\rm i}\gamma$
direction. Here, $\omega = \omega _r + {\rm i}\gamma$![]() , where $\omega _r$
, where $\omega _r$![]() is the real frequency and $\gamma$
is the real frequency and $\gamma$![]() is the imaginary part which corresponds to the growth rate.
is the imaginary part which corresponds to the growth rate.
2.3. Zeroth-order (equilibrium) equations for magnetised electrons
Inserting (2.4) into the governing equations and considering the zeroth-order terms leads to the equilibrium equations. For magnetised electrons, using (2.3) and considering the equilibrium bulk velocity $\boldsymbol {u}_{e0} = (u_{e0x}, u_{e0y}, u_{e0z})^\intercal$![]() , where subscripts $x$
, where subscripts $x$![]() , $y$
, $y$![]() and $z$
and $z$![]() denote the direction, the steady-state momentum equation in $x$
denote the direction, the steady-state momentum equation in $x$![]() and $y$
and $y$![]() directions can be written as
directions can be written as
where $e$![]() is the elementary charge, $T_e$
is the elementary charge, $T_e$![]() is the electron temperature, $m_e$
is the electron temperature, $m_e$![]() is the electron mass and $n_0$
is the electron mass and $n_0$![]() is the equilibrium density, assuming quasineutrality for the equilibrium condition.
is the equilibrium density, assuming quasineutrality for the equilibrium condition.
Recall that the equilibrium density gradient and electric field are considered to exist locally only in $x$![]() direction. Although (2.6) results in $u_{e0x}=0$
direction. Although (2.6) results in $u_{e0x}=0$![]() , (2.5) yields the well-known drifts:
, (2.5) yields the well-known drifts:
where $n_0'={\rm d}n_0/{{\rm d} x}$![]() is the plasma density gradient. The first term in (2.7) is the $\boldsymbol {E} \times \boldsymbol {B}$
is the plasma density gradient. The first term in (2.7) is the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and the second term is the diamagnetic drift, which can be written as $u_E$
drift and the second term is the diamagnetic drift, which can be written as $u_E$![]() and $u_*$
and $u_*$![]() , respectively. The diamagnetic drift does not come from the single-particle trajectory analysis but appears as an equilibrium drift from the fluid theory, whereas the $\boldsymbol {E} \times \boldsymbol {B}$
, respectively. The diamagnetic drift does not come from the single-particle trajectory analysis but appears as an equilibrium drift from the fluid theory, whereas the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift can be derived from single particle trajectories. Nonetheless, the diamagnetic drift is a steady-state bulk velocity that can propagate in the same or opposite direction of the $\boldsymbol {E} \times \boldsymbol {B}$
drift can be derived from single particle trajectories. Nonetheless, the diamagnetic drift is a steady-state bulk velocity that can propagate in the same or opposite direction of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift.
drift.
As the density gradient is only considered in $x$![]() direction and using $u_{e0x} = 0$
direction and using $u_{e0x} = 0$![]() obtained from (2.6), the steady-state conservation of mass can be written as
obtained from (2.6), the steady-state conservation of mass can be written as
This relation shows that $u_{e0y}$![]() is constant in $y$
is constant in $y$![]() direction, i.e. homogeneous, which is consistent with the configuration considered.
direction, i.e. homogeneous, which is consistent with the configuration considered.
2.4. First-order (linear perturbation) equations for magnetised electrons
Let us consider the perturbation terms of the electron bulk velocity to be $\boldsymbol {u}_{e1} = (u_{e1x}, u_{e1y}, 0)^\intercal$![]() for magnetised electrons. Using (2.8), the first-order conservation of mass can be derived from (2.1) as
for magnetised electrons. Using (2.8), the first-order conservation of mass can be derived from (2.1) as
Using the linear perturbation shown in (2.4), the perturbed electron density can be written as
where $\tilde {\omega }= \omega - k_yu_{e0y}$![]() . Note that $u_{e0y}$
. Note that $u_{e0y}$![]() is given in (2.7).
is given in (2.7).
The first-order momentum equation can be derived from (2.2). Note that pressure term leads to
which results in two contributions to the linearised momentum equation. Thus, using (2.11), the first-order momentum equation for magnetised electrons can be given by
where $v_{{\rm th}} = (k_B T_e/m_e)^{1/2}$![]() is the electron thermal speed and $k_n = n_0' / n_0$
is the electron thermal speed and $k_n = n_0' / n_0$![]() is the inverse of the density gradient length scale, which is also defined similarly by Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993) and Smolyakov et al. (Reference Smolyakov, Chapurin, Frias, Koshkarov, Romadanov, Tang, Umansky, Raitses, Kaganovich and Lakhin2016). Taking the perturbation terms in $y$
is the inverse of the density gradient length scale, which is also defined similarly by Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993) and Smolyakov et al. (Reference Smolyakov, Chapurin, Frias, Koshkarov, Romadanov, Tang, Umansky, Raitses, Kaganovich and Lakhin2016). Taking the perturbation terms in $y$![]() direction, e.g. $\phi _1 \exp (-{\rm i}\omega t +{\rm i} k_y y)$
direction, e.g. $\phi _1 \exp (-{\rm i}\omega t +{\rm i} k_y y)$![]() for the electric field using the electrostatic assumption: $\boldsymbol {E}=-\boldsymbol {\nabla } \phi$
for the electric field using the electrostatic assumption: $\boldsymbol {E}=-\boldsymbol {\nabla } \phi$![]() , (2.12) can be written for $x$
, (2.12) can be written for $x$![]() and $y$
and $y$![]() directions as
directions as
where $\omega _{{\rm ce}} = eB_0/m_e$![]() is the electron gyrofrequency. Solving for $u_{e1x}$
is the electron gyrofrequency. Solving for $u_{e1x}$![]() and $u_{e1y}$
and $u_{e1y}$![]() in (2.13) gives
in (2.13) gives
Equations (2.14) and (2.15) are similarly derived in the Rayleigh–Taylor instability analysis (Chen Reference Chen1984). If cold electrons are assumed (i.e. $v_{{\rm th}} = 0$![]() ) and one considers the low-frequency approximation (i.e. $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$
) and one considers the low-frequency approximation (i.e. $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$![]() ), (2.14) and (2.15) reduce to $u_{e1x} = E_{1y}/B_0$
), (2.14) and (2.15) reduce to $u_{e1x} = E_{1y}/B_0$![]() and $u_{e1y}= {\rm i}\tilde {\omega } u_{e1x}/\omega _{{\rm ce}}$
and $u_{e1y}= {\rm i}\tilde {\omega } u_{e1x}/\omega _{{\rm ce}}$![]() , which are equivalent to the perturbed $\boldsymbol {E} \times \boldsymbol {B}$
, which are equivalent to the perturbed $\boldsymbol {E} \times \boldsymbol {B}$![]() and polarisation drifts, respectively. However, it can be seen that the determinant of the matrix in (2.13) becomes negative if $\tilde {\omega }^2 \gg \omega _{{\rm ce}}^2$
and polarisation drifts, respectively. However, it can be seen that the determinant of the matrix in (2.13) becomes negative if $\tilde {\omega }^2 \gg \omega _{{\rm ce}}^2$![]() . In this case, $u_{e1x}$
. In this case, $u_{e1x}$![]() moves in the opposite direction of the perturbed $\boldsymbol {E} \times \boldsymbol {B}$
moves in the opposite direction of the perturbed $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, which seems to be non-physical (see Appendix A for some discussions). Therefore, assuming $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$
drift, which seems to be non-physical (see Appendix A for some discussions). Therefore, assuming $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$![]() and using (2.14) and (2.15), (2.10) can be written as
and using (2.14) and (2.15), (2.10) can be written as

Note that this equation is similar to (10) in Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993), except for the coefficient of the last term in the denominator.
2.5. Dispersion function for unmagnetised ions
Let us derive the zeroth-order equations for unmagnetised ions. If restricting the argument to the cross-field direction ($x$![]() and $y$
and $y$![]() ), that is, neglecting the plasma dynamics in $z$
), that is, neglecting the plasma dynamics in $z$![]() direction (along the magnetic field), the steady-state continuity equation gives, $n_0 u_{i0x} ={\rm const}.$
direction (along the magnetic field), the steady-state continuity equation gives, $n_0 u_{i0x} ={\rm const}.$![]() , where $u_{i0x}$
, where $u_{i0x}$![]() is the equilibrium ion bulk velocity in $x$
is the equilibrium ion bulk velocity in $x$![]() direction. Assuming that the ion bulk velocity is negligible in $y$
direction. Assuming that the ion bulk velocity is negligible in $y$![]() direction (i.e. $u_{i0y} = 0$
direction (i.e. $u_{i0y} = 0$![]() ), the linear perturbation of the ion number density, $n_{i1}$
), the linear perturbation of the ion number density, $n_{i1}$![]() , can be derived from the linearised conservation of mass as
, can be derived from the linearised conservation of mass as
where ${\boldsymbol {u}}_{i1} = (u_{i1x}, u_{i1y},0)^\intercal$![]() is the linear perturbation of the ion bulk velocities.
is the linear perturbation of the ion bulk velocities.
Assuming cold ions ($T_i= 0$![]() , where $T_i$
, where $T_i$![]() is the ion temperature) and only considering perturbation in $y$
is the ion temperature) and only considering perturbation in $y$![]() direction, as shown in (2.4), the linearised momentum equation for unmagnetised ions can be written as
direction, as shown in (2.4), the linearised momentum equation for unmagnetised ions can be written as
where $m_i$![]() is the ion mass. If one further assumes that the effects of $k_n u_{i0x}$
is the ion mass. If one further assumes that the effects of $k_n u_{i0x}$![]() to be small, (2.17) can be reduced to
to be small, (2.17) can be reduced to
This is consistent with the dispersion function used for unmagnetised ions in Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993).
3. Gradient drift instability for partially magnetised plasmas
3.1. Fluid dispersion relation
Assuming quasineutrality and perturbations occur in the azimuthal direction, which are similar assumptions employed for the Rayleigh–Taylor instability theory (Chen Reference Chen1984), and using (2.16) and (2.20), the dispersion relation for partially magnetised plasmas can be derived as
where $\tilde {\omega } = \omega - k_y u_{e0y}$![]() is used throughout the derivation. Here, this drift-shifted frequency can be written as $\tilde {\omega } = \omega - \omega _E - \omega _*,$
is used throughout the derivation. Here, this drift-shifted frequency can be written as $\tilde {\omega } = \omega - \omega _E - \omega _*,$![]() where $\omega _E = k_y u_E$
where $\omega _E = k_y u_E$![]() , $\omega _* = k_y u_*$
, $\omega _* = k_y u_*$![]() , $u_E = - E_0 / B_0$
, $u_E = - E_0 / B_0$![]() and $u_* = - k_n k_B T_e / (e B_0)$
and $u_* = - k_n k_B T_e / (e B_0)$![]() , as can be seen from (2.7). It can be seen that (3.1) yields a third-order equation for $\omega$
, as can be seen from (2.7). It can be seen that (3.1) yields a third-order equation for $\omega$![]() , from which the damping and linear instability growth can be evaluated.
, from which the damping and linear instability growth can be evaluated.
3.2. Instability criteria in the large-wavelength limit
In the limit of a large-wavelength mode, a simplified form of (3.1) can be obtained by neglecting the $k_y \tilde {\omega }$![]() term in the numerator of (3.1) compared with $k_n \omega _{{\rm ce}}$
term in the numerator of (3.1) compared with $k_n \omega _{{\rm ce}}$![]() , that is, $k_y \tilde {\omega } \ll k_n \omega _{{\rm ce}}$
, that is, $k_y \tilde {\omega } \ll k_n \omega _{{\rm ce}}$![]() . In addition, $u_* \omega _{{\rm ce}} = - k_n v_{{\rm th}}^2$
. In addition, $u_* \omega _{{\rm ce}} = - k_n v_{{\rm th}}^2$![]() gives $k_n^2 v_{{\rm th}}^2 = \tilde {u}_*^2 \omega _{{\rm ce}}^2$
gives $k_n^2 v_{{\rm th}}^2 = \tilde {u}_*^2 \omega _{{\rm ce}}^2$![]() , where $\tilde {u}_*=u_*/v_{{\rm th}}$
, where $\tilde {u}_*=u_*/v_{{\rm th}}$![]() . Therefore, in this limit, (3.1) can be written as
. Therefore, in this limit, (3.1) can be written as
For the solution to have an unstable mode, that is, a root with a positive growth rate, the discriminant of (3.2) must be negative. The instability condition can therefore be given by
where $\tilde {u}_E = u_E / v_{{\rm th}}$![]() . By rewriting (3.3) considering $m_e \ll m_i$
. By rewriting (3.3) considering $m_e \ll m_i$![]() , the condition for the partially magnetised plasma to have an unstable mode in the limit of large wavelength can be written as
, the condition for the partially magnetised plasma to have an unstable mode in the limit of large wavelength can be written as
where
As can be seen from (3.4), the two instability criteria can be obtained as (i) $\tilde {u}_*>0$![]() and $F(\tilde {u}_*, \tilde {u}_E) >0$
and $F(\tilde {u}_*, \tilde {u}_E) >0$![]() and (ii) $\tilde {u}_*<0$
and (ii) $\tilde {u}_*<0$![]() and $F(\tilde {u}_*, \tilde {u}_E) <0$
and $F(\tilde {u}_*, \tilde {u}_E) <0$![]() .
.
It can be seen that (3.3), in the limit of $|\tilde {u}_*| \rightarrow 0$![]() and considering $m_e \ll m_i$
and considering $m_e \ll m_i$![]() , reduces to $u_E u_* > 0$
, reduces to $u_E u_* > 0$![]() , which is the instability criterion for the MSHI (Sakawa et al. Reference Sakawa, Joshi, Kaw, Chen and Jain1993). See Appendix B for further discussion about the comparison of the present dispersion relation and MSHI.
, which is the instability criterion for the MSHI (Sakawa et al. Reference Sakawa, Joshi, Kaw, Chen and Jain1993). See Appendix B for further discussion about the comparison of the present dispersion relation and MSHI.
Figure 1 shows the shape of (3.5) for two values of $\tilde {u}_E$![]() , that is, $\tilde {u}_E = -0.1$
, that is, $\tilde {u}_E = -0.1$![]() and $-0.6$
and $-0.6$![]() , to illustrate the range of unstable and stable roots in the limit of large wavelength and low frequency. Here, negative $u_E$
, to illustrate the range of unstable and stable roots in the limit of large wavelength and low frequency. Here, negative $u_E$![]() values are chosen, as the $\boldsymbol {E} \times \boldsymbol {B}$
values are chosen, as the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift occurs in $-y$
drift occurs in $-y$![]() direction when considering $E_0$
direction when considering $E_0$![]() in $x$
in $x$![]() direction and $B_0$
direction and $B_0$![]() in $z$
in $z$![]() direction. Unlike the MSHI that predicts one region for unstable modes, that is, $\tilde {u}_* \tilde {u}_E > 0$
direction. Unlike the MSHI that predicts one region for unstable modes, that is, $\tilde {u}_* \tilde {u}_E > 0$![]() , two unstable regions can be seen in figure 1(a), whereas three unstable regions can be seen in figure 1(b).
, two unstable regions can be seen in figure 1(a), whereas three unstable regions can be seen in figure 1(b).

Figure 1. Cubic function, $F(\tilde {u}_*, \tilde {u}_E)$![]() , shown in (3.5) for (a) $u_E = -0.6 v_{{\rm th}}$
, shown in (3.5) for (a) $u_E = -0.6 v_{{\rm th}}$![]() and (b) $u_E = -0.1 v_{{\rm th}}$
and (b) $u_E = -0.1 v_{{\rm th}}$![]() , resulting in two and three instability regions, respectively. Instabilities occur according to (3.4) in the regions where the product of the $u_*$
, resulting in two and three instability regions, respectively. Instabilities occur according to (3.4) in the regions where the product of the $u_*$![]() and the function $F(\tilde {u}_*, \tilde {u}_E)$
and the function $F(\tilde {u}_*, \tilde {u}_E)$![]() is positive. The red dashed line denotes $F=0$
is positive. The red dashed line denotes $F=0$![]() and the unstable regions are indicated in blue.
and the unstable regions are indicated in blue.
Figure 2 shows the unstable and stable regions of the gradient drift instability in the large-wavelength limit, as a function of the diamagnetic drift and $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. The unstable roots are obtained according to the instability condition shown in (3.4), and the results are consistent with figure 1, showing the two and three unstable regions depending on $u_*$
drift. The unstable roots are obtained according to the instability condition shown in (3.4), and the results are consistent with figure 1, showing the two and three unstable regions depending on $u_*$![]() and $u_E$
and $u_E$![]() . A few observations about the instability criteria can be made as follows.
. A few observations about the instability criteria can be made as follows.
(i) When $|\tilde {u}_E| > 0.3$
 , there are two regions that satisfy the instability condition shown in (3.4). One is $u_E u_*>0$
, there are two regions that satisfy the instability condition shown in (3.4). One is $u_E u_*>0$ , leading to a condition that can be written as $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$
, leading to a condition that can be written as $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$ , which is similar to the MSHI. In this regime, both $\boldsymbol {E} \times \boldsymbol {B}$
, which is similar to the MSHI. In this regime, both $\boldsymbol {E} \times \boldsymbol {B}$ and diamagnetic drifts are in the same direction, leading to instability. The other region that results in instability can be found at $u_* > v_{{\rm th}}$
and diamagnetic drifts are in the same direction, leading to instability. The other region that results in instability can be found at $u_* > v_{{\rm th}}$ while $u_E < 0$
while $u_E < 0$ , as shown in figures 1(a) and 2. It is interesting to note that $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0<0$
, as shown in figures 1(a) and 2. It is interesting to note that $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0<0$ in this second region, which is a different instability criterion compared to the MSHI. This indicates that a strong diamagnetic drift (compared with the magnitude of the $\boldsymbol {E} \times \boldsymbol {B}$
in this second region, which is a different instability criterion compared to the MSHI. This indicates that a strong diamagnetic drift (compared with the magnitude of the $\boldsymbol {E} \times \boldsymbol {B}$ drift and the electron thermal speed) can drive an instability at large wavelength whereas the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$
drift and the electron thermal speed) can drive an instability at large wavelength whereas the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$ drift.
drift.(ii) When $0< |\tilde {u}_E| \lessapprox 0.3$
 , there are three regions that result in linear instability. As can be seen from figure 1(b), $F$
, there are three regions that result in linear instability. As can be seen from figure 1(b), $F$ becomes positive in a certain range within $u_*<0$
becomes positive in a certain range within $u_*<0$ , leading to a stable root because $u_* F < 0$
, leading to a stable root because $u_* F < 0$ . The appearance of a stable mode in the $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$
. The appearance of a stable mode in the $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$ region can also be seen from figure 2. It can be shown from (3.5) that $F\approx (\tilde {u}_*-\tilde {u}_E)(\tilde {u}_*+ \tilde {u}_E - 1 ) (\tilde {u}_*+ \tilde {u}_E + 1 )$
region can also be seen from figure 2. It can be shown from (3.5) that $F\approx (\tilde {u}_*-\tilde {u}_E)(\tilde {u}_*+ \tilde {u}_E - 1 ) (\tilde {u}_*+ \tilde {u}_E + 1 )$ when assuming $|\tilde {u}_E| \ll 1$
when assuming $|\tilde {u}_E| \ll 1$ . Hence, the three instability regions can be observed approximately at (i) $\tilde {u}_* < -1 - \tilde {u}_E$
. Hence, the three instability regions can be observed approximately at (i) $\tilde {u}_* < -1 - \tilde {u}_E$ , (ii) $\tilde {u}_E<\tilde {u}_* < 0$
, (ii) $\tilde {u}_E<\tilde {u}_* < 0$ and (iii) $\tilde {u}_* > 1-\tilde {u}_E$
and (iii) $\tilde {u}_* > 1-\tilde {u}_E$ for $\tilde {u}_E<0$
for $\tilde {u}_E<0$ .
.(iii) When $\tilde {u}_E=0$
 , there are two regions where the unstable roots exist. Equation (3.5) reduces to $F = \tilde {u}_* (\tilde {u}_* - 1 ) (\tilde {u}_* + 1 )$
, there are two regions where the unstable roots exist. Equation (3.5) reduces to $F = \tilde {u}_* (\tilde {u}_* - 1 ) (\tilde {u}_* + 1 )$ when $\tilde {u}_E=0$
when $\tilde {u}_E=0$ . Hence, the instability regions can be observed at (i) $\tilde {u}_* < -1$
. Hence, the instability regions can be observed at (i) $\tilde {u}_* < -1$ , and (ii) $\tilde {u}_* > 1$
, and (ii) $\tilde {u}_* > 1$ , which can be seen from figure 2. The solutions indicate that a low-frequency, large-wavelength instability can occur with a strong diamagnetic drift in the absence of any electric field.
, which can be seen from figure 2. The solutions indicate that a low-frequency, large-wavelength instability can occur with a strong diamagnetic drift in the absence of any electric field.

Figure 2. Unstable and stable regions of the gradient drift instability in the large-wavelength limit, as a function of $u_E$![]() and $u_*$
and $u_*$![]() . The blue region indicates where the unstable modes exist, whereas unstable modes do not exist in the stable region, shown in white.
. The blue region indicates where the unstable modes exist, whereas unstable modes do not exist in the stable region, shown in white.
Figure 3 shows the schematic of the instability criteria for the low-frequency rotating spokes. The first condition $u_E u_*>0$![]() is similar to the MSHI, in which it is predicted that the $\boldsymbol {E} \times \boldsymbol {B}$
is similar to the MSHI, in which it is predicted that the $\boldsymbol {E} \times \boldsymbol {B}$![]() and diamagnetic drifts must be in the same direction. Another instability condition observed from the derivations shown in this section (i.e. (3.4) and (3.5)) illustrates that the partially magnetised plasma can be unstable when the diamagnetic drift is sufficiently larger than the electron thermal speed, even if the electric field and the density gradient exist in the opposite direction.
and diamagnetic drifts must be in the same direction. Another instability condition observed from the derivations shown in this section (i.e. (3.4) and (3.5)) illustrates that the partially magnetised plasma can be unstable when the diamagnetic drift is sufficiently larger than the electron thermal speed, even if the electric field and the density gradient exist in the opposite direction.

Figure 3. Instability criteria for low-frequency rotating spokes. (a) The $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and diamagnetic drift are in the same direction. (b) The $\boldsymbol {E} \times \boldsymbol {B}$
drift and diamagnetic drift are in the same direction. (b) The $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and diamagnetic drift are in the opposite direction and the diamagnetic drift must be larger than the electron thermal speed.
drift and diamagnetic drift are in the opposite direction and the diamagnetic drift must be larger than the electron thermal speed.
3.3. Direction of the wave propagation
When the instability condition is met in (3.3), the real part of the solution in (3.2) can be obtained as
where $c_s=(k_B T_e /m_i)^{1/2}$![]() is the ion acoustic speed. The phase velocity of the wave can be obtained from $v_\phi = \omega _r / k_y$
is the ion acoustic speed. The phase velocity of the wave can be obtained from $v_\phi = \omega _r / k_y$![]() . It can therefore be seen from (3.6) that the wave propagates in the direction of the diamagnetic drift, which may lead to the rotating spokes to propagate in the direction of $\boldsymbol {E} \times \boldsymbol {B}$
. It can therefore be seen from (3.6) that the wave propagates in the direction of the diamagnetic drift, which may lead to the rotating spokes to propagate in the direction of $\boldsymbol {E} \times \boldsymbol {B}$![]() drift or $-\boldsymbol {E} \times \boldsymbol {B}$
drift or $-\boldsymbol {E} \times \boldsymbol {B}$![]() drift, depending on the instability criteria discussed in § 3.2.
drift, depending on the instability criteria discussed in § 3.2.
3.4. Resonance
It can be seen from (2.14) and (2.15) that the linear perturbation of the electron bulk velocities shows resonance when $\tilde {\omega }^2 \approx \omega _{{\rm ce}}^2$![]() . In other words, $\omega \approx \pm \omega _{{\rm ce}} + k_y u_{e0y}$
. In other words, $\omega \approx \pm \omega _{{\rm ce}} + k_y u_{e0y}$![]() , where $u_{e0y}$
, where $u_{e0y}$![]() is the sum of the $\boldsymbol {E} \times \boldsymbol {B}$
is the sum of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and diamagnetic drift, given in (2.7). If the real frequency is of the order of ion plasma frequency, $\omega _r \ll \omega _{{\rm ce}}$
drift and diamagnetic drift, given in (2.7). If the real frequency is of the order of ion plasma frequency, $\omega _r \ll \omega _{{\rm ce}}$![]() , as shown later in § 4, a resonance condition for the dispersion relation can be considered to be
, as shown later in § 4, a resonance condition for the dispersion relation can be considered to be
It can be seen that the smaller (larger) the electron drift, the larger (smaller) $k_y$![]() at which resonance occurs. Equation (3.7) indicates that the electron drift is in resonance with the electron gyromotion, which is akin to the electrostatic two-stream instability where the electron drift is in resonance with the electron plasma frequency.
at which resonance occurs. Equation (3.7) indicates that the electron drift is in resonance with the electron gyromotion, which is akin to the electrostatic two-stream instability where the electron drift is in resonance with the electron plasma frequency.
Equation (3.7) can also be written as $k_y \lambda _D = \tilde {u}_{e0y}^{-1}{\omega _{{\rm ce}}}/{\omega _{{\rm pe}}}$![]() or $k_y r_L = \tilde {u}_{e0y}^{-1}$
or $k_y r_L = \tilde {u}_{e0y}^{-1}$![]() , where $\omega _{{\rm pe}}=(e^2n_0 / m_e \epsilon _0)^{1/2}$
, where $\omega _{{\rm pe}}=(e^2n_0 / m_e \epsilon _0)^{1/2}$![]() is the electron plasma frequency, $\lambda _D = (\epsilon _0 k_B T_e / e^2 n_0)^{1/2}$
is the electron plasma frequency, $\lambda _D = (\epsilon _0 k_B T_e / e^2 n_0)^{1/2}$![]() is the Debye length, $\epsilon _0$
is the Debye length, $\epsilon _0$![]() is the vacuum permittivity, $\tilde {u}_{e0y}=u_{e0y}/v_{{\rm th}}$
is the vacuum permittivity, $\tilde {u}_{e0y}=u_{e0y}/v_{{\rm th}}$![]() and $r_L = v_{{\rm th}}/\omega _{{\rm ce}}$
and $r_L = v_{{\rm th}}/\omega _{{\rm ce}}$![]() is the electron Larmor radius. Although the kinetic effects, such as the electron Bernstein mode leading to electron cyclotron drift instability (Cavalier et al. Reference Cavalier, Lemoine, Bonhomme, Tsikata, Honoré and Grésillon2013; Hara & Tsikata Reference Hara and Tsikata2020), may play an important role when $k_y r_L=O(1)$
is the electron Larmor radius. Although the kinetic effects, such as the electron Bernstein mode leading to electron cyclotron drift instability (Cavalier et al. Reference Cavalier, Lemoine, Bonhomme, Tsikata, Honoré and Grésillon2013; Hara & Tsikata Reference Hara and Tsikata2020), may play an important role when $k_y r_L=O(1)$![]() , the results in the present fluid theory are applicable for the smaller $k_y$
, the results in the present fluid theory are applicable for the smaller $k_y$![]() range, e.g. $k_y r_L<1$
range, e.g. $k_y r_L<1$![]() . Investigation of the coupling of the present fluid theory and the kinetic dispersion relation (Chang & Callen Reference Chang and Callen1992) is reserved for future work.
. Investigation of the coupling of the present fluid theory and the kinetic dispersion relation (Chang & Callen Reference Chang and Callen1992) is reserved for future work.
4. Results
In this section, the results from the linear perturbation theory are discussed. Although the analytic discussions made in § 3.2 are applicable only in the large-wavelength, low-frequency limit, the dispersion relation introduced in (3.1) is valid for a wide range of $k_y$![]() under the assumption of the fluid approach and before the resonance condition as shown in (3.7). It is discussed in this section that the growth rate exhibits a broadband profile and the real frequency is of the order of the ion plasma frequency, which suggests that the wave propagation speed is of the order of the ion acoustic speed.
under the assumption of the fluid approach and before the resonance condition as shown in (3.7). It is discussed in this section that the growth rate exhibits a broadband profile and the real frequency is of the order of the ion plasma frequency, which suggests that the wave propagation speed is of the order of the ion acoustic speed.
The following conditions are considered for two cases: $B_0= 200$![]() G, $n_0=10^{15}\ {\rm m}^{-3}$
G, $n_0=10^{15}\ {\rm m}^{-3}$![]() , the electron temperature is $4$
, the electron temperature is $4$![]() eV and $m_i=40$
eV and $m_i=40$![]() amu (assuming singly charged argon ions). These plasma parameters are representative of low-temperature cross-field plasma sources. Here, the two cases considered are (I) $E_0 = 10\ {\rm kV}\ {\rm m}^{-1}$
amu (assuming singly charged argon ions). These plasma parameters are representative of low-temperature cross-field plasma sources. Here, the two cases considered are (I) $E_0 = 10\ {\rm kV}\ {\rm m}^{-1}$![]() and (II) $E_0 = 4\ {\rm kV}\ {\rm m}^{-1}$
and (II) $E_0 = 4\ {\rm kV}\ {\rm m}^{-1}$![]() . Cases I and II result in $u_E \approx -0.6 v_{{\rm th}}$
. Cases I and II result in $u_E \approx -0.6 v_{{\rm th}}$![]() and $u_E \approx -0.24 v_{{\rm th}}$
and $u_E \approx -0.24 v_{{\rm th}}$![]() , respectively, which correspond to the two and three instability region cases as shown in figure 1. The solution to (3.1) is evaluated for several representative values of $u_*$
, respectively, which correspond to the two and three instability region cases as shown in figure 1. The solution to (3.1) is evaluated for several representative values of $u_*$![]() .
.
4.1. Case I: two instability regions, $u_E \approx -0.6 v_{{\rm th}}$
Figure 4 shows the real and imaginary parts of the solution of (3.1) for different $u_*$![]() values for $u_E \approx -0.6 v_{{\rm th}}$
values for $u_E \approx -0.6 v_{{\rm th}}$![]() . This is consistent with the two instability region case, which occurs when $|u_E| > 0.3$
. This is consistent with the two instability region case, which occurs when $|u_E| > 0.3$![]() , as shown in figure 1(a).
, as shown in figure 1(a).

Figure 4. Case I: two instability regions at large wavelength, for different values of $u_*$![]() with $u_E$
with $u_E$![]() fixed at $u_E = -0.6 v_{{\rm th}}$
fixed at $u_E = -0.6 v_{{\rm th}}$![]() . This value of $u_E = -0.6 v_{{\rm th}}$
. This value of $u_E = -0.6 v_{{\rm th}}$![]() corresponds to the case illustrated in figure 1(a). The real frequency, $\omega _r$
corresponds to the case illustrated in figure 1(a). The real frequency, $\omega _r$![]() , and growth rate, $\gamma$
, and growth rate, $\gamma$![]() , are shown in blue dashed and black solid lines, respectively, for each value of $u_*$
, are shown in blue dashed and black solid lines, respectively, for each value of $u_*$![]() .
.
In the limit of a large positive diamagnetic drift (e.g. $u_* = 1.67 v_{{\rm th}}$![]() as shown in figure 4a), a low-frequency mode is indeed observed in the limit of large wavelength. The real frequency, $\omega _r$
as shown in figure 4a), a low-frequency mode is indeed observed in the limit of large wavelength. The real frequency, $\omega _r$![]() , is positive, indicating that wave propagates in the direction of the diamagnetic drift as opposed to the $\boldsymbol {E} \times \boldsymbol {B}$
, is positive, indicating that wave propagates in the direction of the diamagnetic drift as opposed to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. This observation is consistent with the theoretical observation in § 3.2.
drift. This observation is consistent with the theoretical observation in § 3.2.
Figures 4(b) and 4(c) show that the dispersion relation yields roots with a positive growth rate at a finite $k_y\neq 0$![]() but yields stable solutions in the large-wavelength limit, as the magnitude of the diamagnetic drift decreases. Note that for these cases, $u_E u_*<0$
but yields stable solutions in the large-wavelength limit, as the magnitude of the diamagnetic drift decreases. Note that for these cases, $u_E u_*<0$![]() , that is, the diamagnetic drift is in the direction opposite to the $\boldsymbol {E} \times \boldsymbol {B}$
, that is, the diamagnetic drift is in the direction opposite to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. These results are consistent with the prediction from the analytic theory obtained in § 3.2. It is to be noted that the sign of the real frequency flips, which can be seen from figures 4(b) and 4(c), indicating that the resonance type phenomenon is driven by the diamagnetic drift in figure 4(b). However, the wave propagates in the direction of the $\boldsymbol {E} \times \boldsymbol {B}$
drift. These results are consistent with the prediction from the analytic theory obtained in § 3.2. It is to be noted that the sign of the real frequency flips, which can be seen from figures 4(b) and 4(c), indicating that the resonance type phenomenon is driven by the diamagnetic drift in figure 4(b). However, the wave propagates in the direction of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift in figure 4(c) despite the fact that the magnitude of diamagnetic drift is larger than the $\boldsymbol {E} \times \boldsymbol {B}$
drift in figure 4(c) despite the fact that the magnitude of diamagnetic drift is larger than the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. As the diamagnetic drift approaches zero, the resonance condition shifts towards a larger $k_y \lambda _D$
drift. As the diamagnetic drift approaches zero, the resonance condition shifts towards a larger $k_y \lambda _D$![]() , as shown in (3.7), and the partially magnetised plasma is stable for a wide range of $k_y$
, as shown in (3.7), and the partially magnetised plasma is stable for a wide range of $k_y$![]() .
.
When the diamagnetic drift is in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift (i.e. $u_E u_*>0$
drift (i.e. $u_E u_*>0$![]() ), the results in figure 4(d–f) illustrate that the large-wavelength mode is indeed unstable. This is consistent with § 3.2, in which it is observed that $u_E u_*>0$
), the results in figure 4(d–f) illustrate that the large-wavelength mode is indeed unstable. This is consistent with § 3.2, in which it is observed that $u_E u_*>0$![]() yields a root with a positive growth rate at the large-wavelength, low-frequency limit, if $|u_E|> 0.3 v_{{\rm th}}$
yields a root with a positive growth rate at the large-wavelength, low-frequency limit, if $|u_E|> 0.3 v_{{\rm th}}$![]() . Another observation that can be made is that the real frequency is negative, illustrating that the wave propagates in the direction of both $\boldsymbol {E} \times \boldsymbol {B}$
. Another observation that can be made is that the real frequency is negative, illustrating that the wave propagates in the direction of both $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and diamagnetic drift. The real frequency where the growth rate is maximum is approximately $(5\text {-}6)\omega _{{\rm pi}}$
drift and diamagnetic drift. The real frequency where the growth rate is maximum is approximately $(5\text {-}6)\omega _{{\rm pi}}$![]() , suggesting that the wave propagation speed is of the order of the ion acoustic speed. The cutoff where $\gamma$
, suggesting that the wave propagation speed is of the order of the ion acoustic speed. The cutoff where $\gamma$![]() becomes zero at a finite $k_y$
becomes zero at a finite $k_y$![]() in figure 4(d–f) occurs before the resonance condition discussed in § 3.4.
in figure 4(d–f) occurs before the resonance condition discussed in § 3.4.
4.2. Case II: three instability regions, $u_E \approx -0.24 v_{{\rm th}}$
Figure 5 shows the real and imaginary parts of the solution of (3.1) for several representative $u_*$![]() values for $u_E \approx -0.24 v_{{\rm th}}$
values for $u_E \approx -0.24 v_{{\rm th}}$![]() . As discussed in § 3.2 and shown in figure 1(b), three instability regions can be seen in the large-wavelength limit, when $|u_E| \lessapprox 0.3 v_{{\rm th}}$
. As discussed in § 3.2 and shown in figure 1(b), three instability regions can be seen in the large-wavelength limit, when $|u_E| \lessapprox 0.3 v_{{\rm th}}$![]() .
.

Figure 5. Case II: three instability regions at large wavelength, for different values of $u_*$![]() with $u_E$
with $u_E$![]() fixed at $u_E = -0.24 v_{{\rm th}}$
fixed at $u_E = -0.24 v_{{\rm th}}$![]() . The real frequency, $\omega _r$
. The real frequency, $\omega _r$![]() , and growth rate, $\gamma$
, and growth rate, $\gamma$![]() , are shown in blue dashed and black solid lines, respectively, for each value of $u_*$
, are shown in blue dashed and black solid lines, respectively, for each value of $u_*$![]() . In figure 5(e), the growth rate is zero at $k_y \lambda _D \ll 1$
. In figure 5(e), the growth rate is zero at $k_y \lambda _D \ll 1$![]() , which corresponds to the region where $u_*<0$
, which corresponds to the region where $u_*<0$![]() and $F>0$
and $F>0$![]() , shown in figure 1(b).
, shown in figure 1(b).
Similar to Case I, there is a low-frequency mode at large wavelength when the diamagnetic drift is opposite to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and the magnitude of the diamagnetic drift is sufficiently larger than the electron thermal speed, as shown in figure 5(a). Under this situation, the wave propagation occurs in the direction of the diamagnetic drift. As the magnitude of the diamagnetic drift is decreased, the partially magnetised plasma becomes stable in the large-wavelength limit but a resonance type mode appears, as shown in figures 5(b) and 5(c), similar to Case I. In addition, when the diamagnetic drift is in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$
drift and the magnitude of the diamagnetic drift is sufficiently larger than the electron thermal speed, as shown in figure 5(a). Under this situation, the wave propagation occurs in the direction of the diamagnetic drift. As the magnitude of the diamagnetic drift is decreased, the partially magnetised plasma becomes stable in the large-wavelength limit but a resonance type mode appears, as shown in figures 5(b) and 5(c), similar to Case I. In addition, when the diamagnetic drift is in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, the partially magnetised plasma is unstable in the large-wavelength limit, which can be seen in figures 5(d) and 5( f). However, it is interesting to note that the growth rate becomes zero at $k_y \rightarrow 0$
drift, the partially magnetised plasma is unstable in the large-wavelength limit, which can be seen in figures 5(d) and 5( f). However, it is interesting to note that the growth rate becomes zero at $k_y \rightarrow 0$![]() for the cases with intermediate $u_*$
for the cases with intermediate $u_*$![]() values, as shown in figure 5(e). This is consistent with the theoretical prediction in § 3.2 and figure 1(b): when $|u_E| \lessapprox 0.3 v_{{\rm th}}$
values, as shown in figure 5(e). This is consistent with the theoretical prediction in § 3.2 and figure 1(b): when $|u_E| \lessapprox 0.3 v_{{\rm th}}$![]() , the partially magnetised plasma becomes stable at $k_y \rightarrow 0$
, the partially magnetised plasma becomes stable at $k_y \rightarrow 0$![]() for a range of $u_*$
for a range of $u_*$![]() in which $u_* F<0$
in which $u_* F<0$![]() , as shown in figure 1(b).
, as shown in figure 1(b).
In summary, the partially magnetised plasma dispersion relation using the fluid approach shows that the linear growth rate is positive in the large-wavelength limit not only (i) when $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$![]() but also (ii) when $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 <0$
but also (ii) when $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 <0$![]() and the diamagnetic drift is sufficiently larger than the electron thermal speed. Although the former is similar to the so-called MSHI, the latter suggests that a strong diamagnetic drift may excite large-wavelength, low-frequency plasma oscillations that propagate in the direction of the diamagnetic drift.
and the diamagnetic drift is sufficiently larger than the electron thermal speed. Although the former is similar to the so-called MSHI, the latter suggests that a strong diamagnetic drift may excite large-wavelength, low-frequency plasma oscillations that propagate in the direction of the diamagnetic drift.
5. Application of the gradient drift instability to cross-field plasma sources
Now that we have established the theory of the gradient drift instability, in this section, the theory is applied to various cross-field plasma configurations. Although the theory discussed in the present paper assumes a slab geometry and the real systems are cylindrical, the slab approximation may provide first-order estimates for the local instabilities in cross-field plasma sources. Here, four configurations are considered: (a) Penning discharge, (b) cylindrical magnetron (e.g. for high-power microwave generation), (c) planar magnetron discharge (e.g. for plasma-assisted deposition) and (d) Hall effect thruster (HET), as shown in figure 6.

Figure 6. Application of the gradient drift instability theory to various cross-field plasma devices. Note that the geometries between top and bottom figures are rotated to keep the magnetic field direction consistent, that is, into the page. Blue arrows, that is, $u_{0r}$![]() in (a,b) or $u_{0z}$
in (a,b) or $u_{0z}$![]() in (c,d), indicate the cross-field electron flow, whereas the red arrows indicate the electron drift in the azimuthal direction.
in (c,d), indicate the cross-field electron flow, whereas the red arrows indicate the electron drift in the azimuthal direction.
5.1. Penning discharge
The Penning discharge, as shown in figure 6(a), operates using an outer cylinder as an anode with a cathode placed along the centreline, in addition to an applied axial magnetic field (Hoh Reference Hoh1963; Simon Reference Simon1963). The plasma density is typically largest near the cathode, generating a radially inward plasma density gradient, $\boldsymbol {\nabla }_r n_0<0$![]() . At the same time, the applied electric field is also radially inward, $E_r<0$
. At the same time, the applied electric field is also radially inward, $E_r<0$![]() . Penning discharge typically naturally satisfies the condition $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$
. Penning discharge typically naturally satisfies the condition $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$![]() , that is, the $\boldsymbol {E} \times \boldsymbol {B}$
, that is, the $\boldsymbol {E} \times \boldsymbol {B}$![]() and diamagnetic drifts are in the same direction. Therefore, as shown in figure 3(a), the Penning-type discharge satisfies (3.4), generating a gradient drift instability at low frequency.
and diamagnetic drifts are in the same direction. Therefore, as shown in figure 3(a), the Penning-type discharge satisfies (3.4), generating a gradient drift instability at low frequency.
5.2. Cylindrical magnetron
The cylindrical magnetron, shown in figure 6(b), is used to study critical ionisation velocity (CIV) phenomena (Brenning et al. Reference Brenning, Lundin, Minea, Costin and Vitelaru2013). In addition, such a cross-field configuration is used in high-power microwave sources. For its use as a microwave generator, ion formation is to be avoided because the working principle is that the electrons from the cathode are trapped (i.e. insulated) by the applied or induced magnetic field to generate high-power microwaves (Benford et al. Reference Benford, Swegle and Schamiloglu2015). However, as the devices increase in power and become more compact, plasma generation is unavoidable as the current density in the system increases (Hadas et al. Reference Hadas, Sayapin, Krasik, Bernshtam and Schnitzer2008). Although low-frequency plasma oscillations are not well-studied due to the short pulse operation, it can be seen from figure 6(b) that the partially magnetised plasma is unstable in such configurations, similar to the Penning discharge.
5.3. Planar magnetron discharge
Figure 6(c) shows a schematic of the planar magnetron, used for plasma-assisted sputtering and deposition (Waits Reference Waits1978). An axial electric field and a radial magnetic field are applied close to the cathode surface. The crossed electric and magnetic fields generate electron drifts in the azimuthal direction.
Recent experimental observations in high-power impulse magnetron sputtering (HiPIMS) show that the rotating spoke direction may be a function of the current (Anders & Yang Reference Anders and Yang2017) and can be reversed during a certain operation (Hecimovic et al. Reference Hecimovic, Maszl, von der Gathen, Böke and von Keudell2016). Similar reversal of the rotating spoke propagation is found in a micro-magnetron discharge (Ito et al. Reference Ito, Young and Cappelli2015; Marcovati et al. Reference Marcovati, Ito and Cappelli2020). The global axial plasma profile, such as the location and amplitude of the density and potential gradients, can affect the characteristics of the gradient drift instability, leading to rotating spokes.
In addition, magnetron sputtering devices have a large magnetic field inhomogeneity in the region where the rotating spokes occur, leading to the possibility of gradient drift instabilities due to magnetic field gradients (Esipchuk & Tilinin Reference Esipchuk and Tilinin1976; Tilinin Reference Tilinin1977; Frias et al. Reference Frias, Smolyakov, Kaganovich and Raitses2013) playing an important role in the formation of rotating spokes.
5.4. HET
The HET operates using a radial applied magnetic field and axial electric field, as shown in figure 6(d). In the plume of a HET, the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift is much larger than the diamagnetic drift and the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$
drift is much larger than the diamagnetic drift and the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, which is shown as region 2 in figure 6(d). Consequently, using the instability criteria discussed in (3.4), the partially magnetised plasma in the HET plume is stable against the Penning-type instability. The simulation results by Kawashima et al. (Reference Kawashima, Hara and Komurasaki2018) were compared with a class of gradient drift instabilities in the presence of a magnetic field gradient (Esipchuk & Tilinin Reference Esipchuk and Tilinin1976; Tilinin Reference Tilinin1977; Frias et al. Reference Frias, Smolyakov, Kaganovich and Raitses2013) and showed that the gradient drift instability due to the magnetic field gradient grows in the plume region, which leads to the excitation of rotating spokes.
drift, which is shown as region 2 in figure 6(d). Consequently, using the instability criteria discussed in (3.4), the partially magnetised plasma in the HET plume is stable against the Penning-type instability. The simulation results by Kawashima et al. (Reference Kawashima, Hara and Komurasaki2018) were compared with a class of gradient drift instabilities in the presence of a magnetic field gradient (Esipchuk & Tilinin Reference Esipchuk and Tilinin1976; Tilinin Reference Tilinin1977; Frias et al. Reference Frias, Smolyakov, Kaganovich and Raitses2013) and showed that the gradient drift instability due to the magnetic field gradient grows in the plume region, which leads to the excitation of rotating spokes.
However, if one considers the plasma inside the channel, shown as region 1 in figure 6(d), the cross-field electron transport is primarily driven by the pressure gradient near the anode. It can therefore be considered that the magnitude of the diamagnetic drift is larger than that of the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, while the two drifts may be in the opposite direction. Thus, this condition may lead to the gradient drift instability presented in this paper to be unstable. The spoke rotation will be in the direction of the diamagnetic drift driven by the plasma density gradient inside the channel, which turns out to be in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$
drift, while the two drifts may be in the opposite direction. Thus, this condition may lead to the gradient drift instability presented in this paper to be unstable. The spoke rotation will be in the direction of the diamagnetic drift driven by the plasma density gradient inside the channel, which turns out to be in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift due to the applied electric field (set up by the anode and cathode) in the system.
drift due to the applied electric field (set up by the anode and cathode) in the system.
In summary, there are two scenarios in which azimuthally rotating spokes can occur in HETs and in the planar magnetron discharge. One is due to the instabilities that are caused by the magnetic field gradient. The other possibility is the gradient drift instability, discussed in the present paper, which is caused by the diamagnetic drift in the absence of magnetic field gradients.
6. Conclusion
The present paper has reviewed the fluid dispersion relation of the partially magnetised plasmas. The dispersion relation derived in this paper shows that the partially magnetised plasmas are unstable (i) when $\boldsymbol {E}_0\boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$![]() or (ii) in the presence of a large diamagnetic drift while $\boldsymbol {E}_0\boldsymbol {\cdot }\boldsymbol {\nabla } n_0 <0$
or (ii) in the presence of a large diamagnetic drift while $\boldsymbol {E}_0\boldsymbol {\cdot }\boldsymbol {\nabla } n_0 <0$![]() . The former is consistent with the so-called MSHI where the $\boldsymbol {E} \times \boldsymbol {B}$
. The former is consistent with the so-called MSHI where the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift and the diamagnetic drift are in the same direction. The latter is an instability that occurs when the diamagnetic drift is sufficiently larger than the electron thermal speed while occurring in the direction against the $\boldsymbol {E} \times \boldsymbol {B}$
drift and the diamagnetic drift are in the same direction. The latter is an instability that occurs when the diamagnetic drift is sufficiently larger than the electron thermal speed while occurring in the direction against the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. One similarity between the two instability conditions is that the plasma wave in the large-wavelength limit propagates in the direction of the diamagnetic drift. This indicates that the low-frequency, large-wavelength, partially magnetised plasma oscillations can occur in either $\boldsymbol {E} \times \boldsymbol {B}$
drift. One similarity between the two instability conditions is that the plasma wave in the large-wavelength limit propagates in the direction of the diamagnetic drift. This indicates that the low-frequency, large-wavelength, partially magnetised plasma oscillations can occur in either $\boldsymbol {E} \times \boldsymbol {B}$![]() or $-\boldsymbol {E} \times \boldsymbol {B}$
or $-\boldsymbol {E} \times \boldsymbol {B}$![]() direction, depending on the plasma conditions.
direction, depending on the plasma conditions.
Acknowledgements
This material is based on work supported by the US Department of Energy, Office of Science, Office of Fusion Energy Sciences, under Award No. DE-SC0020623, by the Air Force Office of Scientific Research under Awards No. FA9550-18-1-0090 and No. FA9550-21-1-0433, and by the Office of Naval Research under Award No. N00014-21-1-2698.
Editor Edward Thomas, Jr. thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Authors contributions
K.H. derived the theory and held discussions with A.R.M. and S.T. Results were prepared by K.H. and all authors contributed to analysing data, reaching conclusions and in writing the paper.
Appendix A. Effect of $\tilde {\omega }^2$ in the electron bulk velocity dispersion
in the electron bulk velocity dispersion
In (2.16), it is assumed that $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$![]() . In the limit of large $k_y$
. In the limit of large $k_y$![]() , the fluid dispersion relation, shown in (3.1), can be written as
, the fluid dispersion relation, shown in (3.1), can be written as
The solution to the dispersion relation yields three roots, that is, $\omega = \pm k_y c_s, k_y u_{e0y}$![]() . Thus, there are no growth rates in the limit of $k_y \rightarrow \infty$
. Thus, there are no growth rates in the limit of $k_y \rightarrow \infty$![]() in figures 4 and 5.
in figures 4 and 5.
If one retains the $\tilde {\omega }^2$![]() term in (2.14) and (2.15), the electron density perturbation term can be written as,
term in (2.14) and (2.15), the electron density perturbation term can be written as,

Combining (A2) and (2.20), a third-order equation can be constructed for $\omega$![]() . For this case, the dispersion relation in the limit of $k_y \rightarrow \infty$
. For this case, the dispersion relation in the limit of $k_y \rightarrow \infty$![]() can be given by
can be given by
In (A3), one solution is always real, that is, $\omega =k_y u_{e0y}$![]() . However, the other two solutions must be evaluated separately. Using $m_e \ll m_i$
. However, the other two solutions must be evaluated separately. Using $m_e \ll m_i$![]() , (A3) can be rewritten as
, (A3) can be rewritten as
The discriminant of (A4) can be obtained as
which can be seen to be negative (i.e. $D<0$![]() ), because $m_e \ll m_i$
), because $m_e \ll m_i$![]() . Thus, these two solutions are not real and become imaginary at $k_y \rightarrow \infty$
. Thus, these two solutions are not real and become imaginary at $k_y \rightarrow \infty$![]() .
.
Although the inclusion of the $\tilde {\omega }^3$![]() term affects the results in the larger $k_y$
term affects the results in the larger $k_y$![]() region, the large-wavelength solutions ($k_y \lambda _D < 1$
region, the large-wavelength solutions ($k_y \lambda _D < 1$![]() ) shown in figures 4 and 5 are not affected by the inclusion of the $\tilde {\omega }^3$
) shown in figures 4 and 5 are not affected by the inclusion of the $\tilde {\omega }^3$![]() term. Therefore, in the present paper, the derivations and results neglecting the $\tilde {\omega }^3$
term. Therefore, in the present paper, the derivations and results neglecting the $\tilde {\omega }^3$![]() term in (A2) are shown.
term in (A2) are shown.
Appendix B. Comparison with MSHI theory
The condition for gradient drift instability shown in (3.4) and (3.5) is different from the condition that is originally proposed by Simon (Simon Reference Simon1963), that is, $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$![]() .
.
To derive a dispersion relation similar to the MSHI (Sakawa et al. Reference Sakawa, Joshi, Kaw, Chen and Jain1993), $|\tilde {u}_*|\ll 1$![]() and $k_y\rightarrow 0$
and $k_y\rightarrow 0$![]() can be assumed so that (3.1) reduces to
can be assumed so that (3.1) reduces to
where $c_s = (k_B T_e / m_i)^{1/2}$![]() is the ion acoustic speed. Assuming $m_e \ll m_i$
is the ion acoustic speed. Assuming $m_e \ll m_i$![]() , the instability criterion from (B1) can be derived as $u_*(u_E - u_*)>0,$
, the instability criterion from (B1) can be derived as $u_*(u_E - u_*)>0,$![]() which leads to $|u_E|>|u_*|$
which leads to $|u_E|>|u_*|$![]() and $u_E u_* >0$
and $u_E u_* >0$![]() . This means that, assuming $|\tilde {u}_*|\ll 1$
. This means that, assuming $|\tilde {u}_*|\ll 1$![]() , a positive growth rate can be obtained only when the magnitude of diamagnetic drift is larger than that of $\boldsymbol {E}\times \boldsymbol {B}$
, a positive growth rate can be obtained only when the magnitude of diamagnetic drift is larger than that of $\boldsymbol {E}\times \boldsymbol {B}$![]() drift and $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$
drift and $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$![]() are both satisfied.
are both satisfied.
It should be noted that the dispersion relation proposed by Sakawa et al. (Reference Sakawa, Joshi, Kaw, Chen and Jain1993) omitted a factor of two in the last term of the denominator of the right-hand side in (3.1). This results in a dispersion relation that omits the $\omega _*$![]() term in the denominator in (B1), leading to the instability condition to be unconditionally $u_* u_E >0$
term in the denominator in (B1), leading to the instability condition to be unconditionally $u_* u_E >0$![]() and therefore $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$
and therefore $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$![]() . It is discussed in § 3.2 that the MSHI can be recovered in the limit of $|\tilde {u}_*| \rightarrow 0$
. It is discussed in § 3.2 that the MSHI can be recovered in the limit of $|\tilde {u}_*| \rightarrow 0$![]() , which can be seen from (B1) as well.
, which can be seen from (B1) as well.