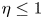Hostname: page-component-77c89778f8-5wvtr Total loading time: 0 Render date: 2024-07-18T02:07:22.237Z Has data issue: false hasContentIssue false
  • English
  • Français

Propagation characteristics of parallel propagating waves in a relativistic magnetized electron plasma

Published online by Cambridge University Press:  14 January 2022

Waseem Khan Open the ORCID record for Waseem Khan [Opens in a new window] ,
M Ali Open the ORCID record for M Ali [Opens in a new window] ,
Ayesha Kanwal ,
Huzaifa Bilal ,
Tajammal H. Khokhar Open the ORCID record for Tajammal H. Khokhar [Opens in a new window]  and
Yousaf Habib
Waseem Khan
Affiliation:
Department of Physical Electronics, Faculty of Science, Masaryk University, Kotlářská 2, Brno611 37, Czech Republic
M Ali
Affiliation:
School of Natural Sciences (SNS), National University of Sciences and Technology (NUST), Islamabad44000, Pakistan
Ayesha Kanwal
Affiliation:
School of Natural Sciences (SNS), National University of Sciences and Technology (NUST), Islamabad44000, Pakistan
Huzaifa Bilal
Affiliation:
School of Natural Sciences (SNS), National University of Sciences and Technology (NUST), Islamabad44000, Pakistan
Tajammal H. Khokhar
Affiliation:
School of Natural Sciences (SNS), National University of Sciences and Technology (NUST), Islamabad44000, Pakistan
Yousaf Habib
Affiliation:
Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, Pakistan
Rights & Permissions [Opens in a new window]

Abstract

Propagation characteristics (propagation regions and cutoffs) of parallel propagating modes (Langmuir, right- and left-handed circularly polarized waves) are studied for relativistic, weakly relativistic and non-relativistic magnetized electron plasma using the kinetic model. The dispersion relation for parallel propagating modes in relativistic electron plasma is investigated by employing the Maxwell–Boltzmann–J üttner distribution function and the final dispersion relation obtained is more general since no approximation is used. As the integrals in the relativistic dispersion relation cannot be done analytically so these integrals have been solved with the numerical quadrature approach. For $\eta \leq 1$ (ratio of rest mass energy to thermal energy), the increase in the effective mass of electrons will result in a change in the mass-dependent quantities (plasma frequency, electron cyclotron frequency, electron sound velocity, etc.) which in turn significantly affect the propagation characteristics of parallel propagating modes. It is observed that the propagation region for these parallel propagating modes decreases and cutoff points are shifted to lower values when we consider a relativistic plasma environment. Moreover, a low-density and high-temperature plasma is more transparent as compared with a high-density and low-temperature plasma for these modes.

Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 905880101
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press.

1. Introduction

Plasma parameters like density, magnetic field and temperature vary over a wide range in various space and laboratory plasma environments. On the basis of these parameters we can classify these environments as being non-relativistic, weakly relativistic, relativistic, degenerate, relativistic degenerate, magnetized, cold and hot plasmas. The characteristics of the waves (propagation, cutoff and resonance) are modified in these plasma environments since the plasma frequency, thermal velocity and cyclotron frequency do not remain the same. In a plasma environment, the relativistic effects become prominent when thermal energy $(k_{B}T)$ of the particles approaches their rest mass energy $(m_{o}c^2)$ (Hazeltine & Waelbroeck Reference Hazeltine and Waelbroeck2018) and in turn the linear and nonlinear behaviour of plasma waves is strongly influenced (Pelletier & Marcowith Reference Pelletier and Marcowith1998; Ghosh et al. Reference Ghosh2012). Magnetized relativistic environments are known to exist in different situations like in active galactic nuclei (jets produced by the rotation of heavy black holes) (Petropoulou et al. Reference Petropoulou2019), other astrophysical objects (such as neutron stars, pulsars, micro-quasars, etc.) (Beskin et al. Reference Beskin1988; Chabrier et al. Reference Chabrier2002; Melrose Reference Melrose2017) and Van Allen radiation belts (Horne et al. Reference Horne2005), and also have primary importance in tokamak plasmas (Bandaru et al. Reference Bandaru2019) and laser–plasma interactions (Banerjee et al. Reference Banerjee2002).

Extensive literature is available which discusses parallel propagating waves in relativistic plasma environments under certain conditions and limitations. Lerche (Reference Lerche1968) discussed these waves in a relativistic environment and found that there will be resonant diffusion only when relativistic particles are present. He used the assumptions of ultra-relativistic plasma and high-phase refractive index. Melrose & Gedalin (Reference Melrose and Gedalin1999) used the relativistic plasma dispersion function to derive the properties of these waves in the extremely relativistic case. Asenjo et al. (Reference Asenjo2009) used magnetofluid unification formalism to derive the dispersion relation of circularly polarized waves along a constant magnetic field. It was concluded that when relativistic effects are larger the electromagnetic wave becomes a non-dispersive light wave. The particle velocities are assumed to be purely transverse with respect to the magnetic field which means that no pressure or density fluctuation is considered. Lazar & Schlickeiser (Reference Lazar and Schlickeiser2006) derived a relativistically correct dispersion relation of parallel propagating waves in magnetized thermal plasma of non-relativistic temperature. Schlickeiser (Reference Schlickeiser1998) solved the dispersion relation of parallel propagating waves analytically for the case of superluminal (waves with phase speed greater than the speed of light) and subluminal (waves with phase speed less than the speed of light) waves. Abbas et al. (Reference Abbas2012) discussed both parallel and perpendicular propagating waves in weakly magnetized relativistic plasma under various limits and observed that the propagation region broadens as the plasma environment gets more relativistic. Khan et al. (Reference Khan2020a) applied the weak magnetic field limit on parallel propagating waves in a relativistic plasma environment and found a shift in cutoff points towards lower values of the frequency. Sazhin (Reference Sazhin1987) presented an approximate analysis of different types of electromagnetic wave propagation in a weakly relativistic electron plasma. He deduced that in the vicinity of certain frequencies, relativistic effects on the refractive index of these waves cannot be disregarded even when the electron energy is quite small. He concluded that the frequencies corresponding to the cutoffs in a weakly relativistic plasma are shifted compared with the frequencies corresponding to the cutoffs in a cold plasma, so that the frequency range of possible wave propagation increases.

We do find research articles where the dispersion relation of parallel propagating modes in a relativistic plasma environment is derived but, unfortunately, in order to solve the integral that contains relativistic momentum (which cannot be solved analytically) certain approximations ($\omega < k v,\ \omega >k v$) are used. However, we have tried to solve these integrals numerically without using any approximation. There has been extensive work done by Kepppens et al. to present a relativistically complete two-fluid analysis for a pair plasma. They discuss the advantages of using the governing 12th-degree polynomial in the wave frequency $\omega$ which represents 12 non-trivial waves and that can be separated into six pairs of forward- and backward-propagating waves, as the polynomial is sixth order in $\omega ^2$ (Keppens & Goedbloed Reference Keppens and Goedbloed2019; Keppens et al. Reference Keppens2019; De Jonghe & Keppens Reference De Jonghe and Keppens2020). But we know that an ideal two-fluid viewpoint fails to describe wave–particle interactions. So, we cannot discuss wave propagation for different particle velocities using this model.

The paper is organized as follows. Section 2 consists of the general formalism and dispersion relation for parallel propagating waves. The numerical approach we use is presented in § 3 and § 4 deals with the graphical analysis and discussion. Lastly, § 5 presents the conclusion of our paper.

2. Parallel propagating waves in magnetized relativistic plasma

The generalized expression for the plasma conductivity tensor (Abbas et al. Reference Abbas2012; Khan et al. Reference Khan2020a) is given as

(2.1)\begin{align} \sigma_{\alpha\beta}& = \sum_s\frac{q^2n_0}{\omega}{\int_{0}^{\infty}}{\int_{0}^{\rm \pi}}{\int_{0}^{2 {\rm \pi}}}p^2\sin{\theta}\,{\textrm{d}\theta}\, \textrm{d} p\,{\textrm{d} \phi'} \frac{v_\alpha}{\varOmega} \nonumber\\ & \quad {\int_{-\infty}^{\phi}}\, \textrm{d} \phi'\exp \left[\frac{1}{\varOmega}({(-\textrm{i}{\omega} +\textrm{i}{k_zv\cos{\theta}})(\phi-\phi')} \right. \nonumber\\ & \left.\vphantom{\frac{1}{\varOmega}}+\textrm{i}{k_x}{v}\sin{\theta}(\sin{\phi- \sin\phi'}))\right] \left[(\omega-\boldsymbol{k}\cdot\boldsymbol{v})\frac{\partial{f_{o}}}{\partial{{p}_\beta}} +{v_\beta}\left(\boldsymbol{k}\cdot\frac{\partial{f_{o}}}{\partial{\boldsymbol{p}}}\right)\right]. \end{align}

Here $q$, $n_0$, $\varOmega$, $\sum _s$ and $f_0$ are the electron charge, equilibrium number density, relativistic cyclotron frequency, sum over species and equilibrium distribution function, respectively. The velocity $\boldsymbol {v}$ in spherical coordinates is given as

(2.2)\begin{equation} \boldsymbol{v}=(v\sin\theta\cos\phi,v\sin\theta\sin\phi,v\cos\theta). \end{equation}

The wave vector $\boldsymbol {k}$ for parallel propagation is taken as

(2.3)\begin{equation} \boldsymbol{k}=k_z\hat{z}. \end{equation}

The relativistic velocity $\boldsymbol {v}$ and the relativistic cyclotron frequency ${\varOmega }$ are defined as

(2.4)\begin{equation} v=\frac{cp}{(m^2c^2+p^2)}^{1/2} \end{equation}

and

(2.5)\begin{equation} \varOmega=\frac{\omega_{ce}}{\gamma}, \end{equation}

where ${\gamma }$ is the relativistic factor given as

(2.6)\begin{equation} \gamma=\left(1+\frac{p^2}{m^2c^2}\right)^{1/2}. \end{equation}

Here we are considering electron–ion plasma but since the waves under our consideration are high-frequency waves so ion dynamics is not included. This is the reason why we drop the summation over the species from now on. To derive the dispersion relation for parallel propagating waves the following dyadic is used (Montgomery & Tidman Reference Montgomery and Tidman1964; Schlickeiser Reference Schlickeiser1998):

(2.7)\begin{equation} R_{\alpha\beta} =(\omega^2-c^2k^2)\delta_{\alpha\beta}+c^2{k_\alpha}k_\beta+ 4{\rm \pi}\iota\omega\sigma_{\alpha\beta};\end{equation}

and we take propagation vector $\boldsymbol {k}$ in the direction of magnetic field $\boldsymbol {B}$ that is in the $z$ direction. So the required components of the dyadic are given as

(2.8)\begin{gather} R_{xx} =\omega^2-c^2k^2+4{\rm \pi}\iota\omega\sigma_{xx}, \end{gather}
(2.9)\begin{gather}R_{xy}={-}R_{yx} =4{\rm \pi}\iota\omega\sigma_{xy}, \end{gather}
(2.10)\begin{gather}R_{zz} =\omega^2+4{\rm \pi}\iota\omega\sigma_{zz}, \end{gather}

where $\sigma _{xx}$, $\sigma _{xy}$ and $\sigma _{zz}$ are components of the conductivity tensor and are written as

(2.11)\begin{align} \sigma_{xx}& ={-q^2n_0}\int_{0}^{\infty}p^2 \frac{\partial{f_0}}{\partial{p}}\, \textrm{d} {p}\int_{0}^{\rm \pi} \frac{v}{\varOmega}\sin^3{\theta}\,{\textrm{d} \theta}\int_{0}^{2{\rm \pi}} \cos\phi \nonumber\\ & \quad\times\cos(\phi-\alpha)\, \textrm{d} \phi\int_{\infty}^{0}\exp \left[{\frac{-\textrm{i}}{\varOmega}}(\omega-{k_z}v\cos{\theta})\alpha \right]\, \textrm{d} \alpha, \end{align}
(2.12)\begin{align} \sigma_{xy}& ={-q^2n_0}\int_{0}^{\infty}p^2 \frac{\partial{f_0}}{\partial{p}}\, \textrm{d} p\int_{0}^{\rm \pi} \frac{v}{\varOmega}\sin^3{\theta}\, \textrm{d} \theta\int_{0}^{2{\rm \pi}} \cos\phi \nonumber\\ & \quad \times\sin(\phi-\alpha)\, \textrm{d} \phi\int_{\infty}^{0} \exp\left[\frac{-\textrm{i}}{\varOmega}(\omega-{k_z}v\cos{\theta})\alpha\right]\, \textrm{d} \alpha \end{align}

and

(2.13)\begin{align} \sigma_{zz}& ={-q^2n_0}\int_{0}^{\infty}p^2 \frac{\partial{f_0}}{\partial{p}}\, \textrm{d} {p}\int_{0}^{\rm \pi} \frac{v}{\varOmega}\cos^2{\theta}\sin{\theta}\, \textrm{d} \theta \int_{0}^{2{\rm \pi}}\,{\textrm{d} \phi} \nonumber\\ & \quad\int_{\infty}^{0}\exp\left[{\frac{-\textrm{i}}{\varOmega}}(\omega- {k_z}v\cos{\theta})\alpha \right]\, \textrm{d} \alpha. \end{align}

By using the integrals

(2.14)\begin{gather} \int_{0}^{2{\rm \pi}}\cos\phi{\cos}(\phi-\alpha)\, \textrm{d} \phi={\rm \pi}\cos{\alpha}, \end{gather}
(2.15)\begin{gather}\int_{\infty}^{0}\cos{\alpha}\exp\left[{\frac{-\textrm{i}}{\varOmega}}(\omega- {k_z}v\cos{\theta})\alpha\right]{\textrm{d}\alpha}=\frac{\textrm{i}\varOmega(\omega- {k_z}v\cos{\theta})}{(\omega-{k_z}v\cos{\theta})^2-\varOmega^2} \end{gather}

in (2.11) and after performing $\theta$ integration we can write

(2.16)\begin{align} \sigma_{xx}& ={-}{n_0}\, \textrm{e}^2\, \textrm{i}{\rm \pi}\int_{0}^{\infty}{p^2} \frac{\partial{f_0}}{\partial{p}}\, \textrm{d} p\frac{1}{2k_z^3v^2} \left(\vphantom{\frac{1}{2k_z^3v^2}}4{k_z}{v}\omega+(\omega-{k_z}{v}\right. \nonumber\\ & \quad -\varOmega)(\omega-{k_z}{v}-\varOmega)\log \left[\frac{\omega-{k_z}{v}-\varOmega}{\omega+{k_z}{v}- \varOmega}\right]+(\omega-{k_z}{v}+\varOmega) \nonumber\\ & \quad \left.(\omega+{k_z}{v}+\varOmega)\log\left[\frac{\omega-{k_z}{v} +\varOmega}{\omega+{k_z}{v}+\varOmega}\right]\right). \end{align}

Similarly, the other two components can also be simplified as

(2.17)\begin{align} \sigma_{xy}& ={-}{n_0}\, \textrm{e}^2{\rm \pi}\int_{0}^{\infty}{p^2} \frac{\partial{f_0}}{\partial{p}}\, \textrm{d} p \frac{1}{2{k_z^3}v^2}\left(\vphantom{\left.(\omega+{k_z}{v}+\varOmega)\log\left[\frac{\omega-{k_z}{v}+ \varOmega}{\omega+{k_z}{v}+\varOmega}\right]\right)}4{k_z}{v}\varOmega-(\omega-{k_z}{v}\right. \nonumber\\ & \quad -\varOmega)(\omega+{k_z}{v}-\varOmega) \log\left[\frac{\omega-{k_z}{v}-\varOmega}{\omega+{k_z}{v}- \varOmega}\right]+(\omega-{k_z}{v}+\varOmega) \nonumber\\ & \quad \left.(\omega+{k_z}{v}+\varOmega)\log\left[\frac{\omega-{k_z}{v}+ \varOmega}{\omega+{k_z}{v}+\varOmega}\right]\right) \end{align}

and

(2.18)\begin{equation} \sigma_{zz}={-}{2n_0}\, \textrm{e}^2\, \textrm{i}{\rm \pi}\int_{0}^{\infty}{p^2} \frac{\partial{f_0}}{\partial\boldsymbol{p}}\, \textrm{d} p\left(\frac{\omega^2}{k_z^3v^3} \left(2\frac{k_zv}{\omega}+\log\left[\frac{\omega-{k_z}{v}}{\omega +{k_z}{v}}\right]\right)\right).\end{equation}

Classical non-interacting particles at thermal equilibrium can be described by the Maxwell–Boltzmann distribution whereas to include the relativistic effects we need to use the Maxwell–Jüttner equilibrium distribution function (MJDF) (Buti Reference Buti1963; Montgomery & Tidman Reference Montgomery and Tidman1964; Georgiou Reference Georgiou1996; Ali et al. Reference Ali2019; Khan et al. Reference Khan2020b,Reference Khanc), given as

(2.19)\begin{equation} f_0(\boldsymbol{p}) =\frac{1}{4{\rm \pi}{m^3c^3}}\frac{\eta}{K_2(\eta)} \exp[-\eta{\gamma}],\end{equation}

where $\eta ={mc^2}/{k_BT}$ (ratio of rest mass energy to thermal energy) and $K_2$ is the modified Bessel function of the second kind of order two.

After substituting the MJDF in (2.16)–(2.18) and using the obtained values of $\sigma _{xx}$, $\sigma _{xy}$ and $\sigma _{zz}$ in (2.8), (2.9) and (2.10), respectively, we get

(2.20)\begin{align} R_{xx}& =\omega^2-c^2k_z^2-\frac{\omega^2_{pe}}{8}\frac{\omega}{ck_z} \frac{\eta^2}{K_2(\eta)}{\int_{0}^{\infty}}z(1+z^2)^{{1}/{2}}\nonumber\\ & \quad \times\exp[-\eta(1+z^2)^{{1}/{2}}]\left(\vphantom{\left.\log\left|\frac{\displaystyle\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}+ \frac{\omega_{ce}}{ck_z}\frac{1}{(1 +z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_zc+ \displaystyle\frac{z}{(1+ z^2)^{{1}/{2}}}+\frac{\omega_{ce}}{ck_z} \frac{1}{(1+ z^2)^{{1}/{2}}}}} \right| \right)}4\frac{\omega}{ck_z} \frac{z}{(1+z^2)^{{1}/{2}}}+\left(\frac{\omega}{ck_z} -\frac{z}{(1+z^2)^{{1}/{2}}}\right.\right.\nonumber\\ & \quad \left.-\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right) \left(\frac{\omega}{ck_z}+\frac{z}{(1+z^2)^{{1}/{2}}}- \frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right)\nonumber\\ & \quad \log\left|\frac{\displaystyle\frac{\omega}{ck_z}- \frac{z}{(1+z^2)^{{1}/{2}}}- \frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_z}+ \frac{z}{(1+z^2)^{{1}/{2}}}-\frac{\omega_{ce}}{ck_z} \frac{1}{(1+z^2)^{{1}/{2}}}} \right|+ \left(\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}\right.\nonumber\\ & \quad \left.+\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right) \left(\frac{\omega}{ck_z}+\frac{z}{(1+z^2)^{{1}/{2}}} +\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right)\nonumber\\ & \quad \left.\log\left|\frac{\displaystyle\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}+ \frac{\omega_{ce}}{ck_z}\frac{1}{(1 +z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_zc+ \displaystyle\frac{z}{(1+ z^2)^{{1}/{2}}}+\frac{\omega_{ce}}{ck_z} \frac{1}{(1+ z^2)^{{1}/{2}}}}} \right| \right)\, \textrm{d} z, \end{align}
(2.21)\begin{align} R_{xy}& ={-}R_{yx}={-}\iota\frac{\omega^2_{pe}}{8} \frac{\omega}{ck_z}\frac{\eta^2}{K_2(\eta)}{\int_{0}^{\infty}} z(1+z^2)^{{1}/{2}}\nonumber\\ & \quad \times\exp[-\eta(1+z^2)^{{1}/{2}}]\left(\vphantom{\left.\log\left|\frac{\displaystyle\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}+ \frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_z}+ \frac{z}{(1+z^2)^{{1}/{2}}}+\frac{\omega_{ce}}{ck_z} \frac{1}{(1+z^2)^{{1}/{2}}}} \right| \right)}4\frac{\omega_{ce}}{ck_z} \frac{z}{(1+z^2)} -\left(\frac{\omega}{ck_z}- \frac{z}{(1+z^2)^{{1}/{2}}}\right.\right. \nonumber\\ & \quad \left.-\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right) \left(\frac{\omega}{ck_z}+\frac{z}{(1+z^2)^{{1}/{2}}}- \frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right)\nonumber\\ & \quad \log\left|\frac{\displaystyle\frac{\omega}{ck_z} -\frac{z}{(1+z^2)^{{1}/{2}}}- \frac{\omega_{ce}}{ck_z}\frac{1}{(1 +z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_z}+ \frac{z}{(1+z^2)^{{1}/{2}}}-\frac{\omega_{ce}}{ck_z} \frac{1}{(1+z^2)^{{1}/{2}}}} \right| + \left(\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}\right.\nonumber\\ & \quad \left.+\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right) \left(\frac{\omega}{ck_z}+\frac{z}{(1+z^2)^{{1}/{2}}} +\frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}\right)\nonumber\\ & \quad \left.\log\left|\frac{\displaystyle\frac{\omega}{ck_z}-\frac{z}{(1+z^2)^{{1}/{2}}}+ \frac{\omega_{ce}}{ck_z}\frac{1}{(1+z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_z}+ \frac{z}{(1+z^2)^{{1}/{2}}}+\frac{\omega_{ce}}{ck_z} \frac{1}{(1+z^2)^{{1}/{2}}}} \right| \right)\, \textrm{d} z \end{align}

and

(2.22)\begin{align} R_{zz}& =\omega^2+\frac{\omega^2_{pe}}{2}\frac{\omega^3}{c^3k_z^3} \frac{\eta^2}{K_2(\eta)}{\int_{0}^{\infty}}z(1+z^2)^{{1}/{2}} \exp[-\eta(1+z^2)^{{1}/{2}}]\nonumber\\ & \quad \times\left(2\frac{ck_z}{\omega}\frac{z}{(1+z^2)^{{1}/{2}}} +\log\left|\frac{\displaystyle\frac{\omega}{ck_z}-\frac{z}{(1 +z^2)^{{1}/{2}}}}{\displaystyle\frac{\omega}{ck_z}+\frac{z}{(1+z^2)^{{1}/{2}}}} \right|\right)\, \textrm{d} z, \end{align}

where $z={p}/{mc}$ and $\omega _{pe}$, $\omega _{ce}$ are the plasma and cyclotron frequency of electrons, respectively. The integrals involved in (2.21), (2.22) and (3.1) cannot be done analytically, so these are computed numerically using the trapezoidal rule (Buti Reference Buti1963; Evans Reference Evans1993; Georgiou Reference Georgiou1996; Burden & Faires Reference Burden and Faires1997; Yang Reference Yang2014; Ali et al. Reference Ali2019; Khan et al. Reference Khan2020b,Reference Khanc).

3. Dispersion relation

In this section we present the dispersion relation of the parallel propagating waves in magnetized fully relativistic plasma which can be analysed for relativistic $(\eta < 1)$, weakly relativistic $(\eta > 1)$ and non-relativistic $(\eta \gg 1)$ environments.

Langmuir waves. The dispersion relation for Langmuir waves is given as

(3.1)\begin{equation} R_{zz}=0.\end{equation}

Right- and left-hand circularly polarized modes. The dispersion relation for $R$-wave and $L$-wave is given as

(3.2)\begin{equation} R_{xx}\pm\textrm{i}R_{xy} =0,\end{equation}

where the plus and minus signs represent right and left circularly polarized modes, respectively. The integrals involved in the dispersion relations cannot be solved analytically since no explicit anti-derivative exists for these integrals. However, we can solve these integrals numerically.

4. Discussion and graphical representation

As we know that the Langmuir mode remains unaffected by the magnetic field, so it is expected to get the same curves as presented in Khan et al. (Reference Khan2020a) for the case of the weak magnetic field. However, the propagation of $R$- and $L$-waves depends on the magnetic field so the dispersion curves will be modified as we are not applying the weak field limit.

In figures 1–3, the dispersion curves for Langmuir waves are analysed for different environments, i.e. relativistic, weakly relativistic and non-relativistic depending on the value of $\eta = m_{0}c^{2}/k_{B}T$. On comparing these three environments, it is found that as the plasma environment becomes more relativistic the cutoff points are shifted towards lower frequencies and the propagation region of the Langmuir wave broadens as reported earlier (Khan et al. Reference Khan2020a). However, the results presented here are more general since no approximation is used in deriving the dispersion relation. In figure 4, we tried to retrieve the results of Melrose & Gedalin (Reference Melrose and Gedalin1999). Here we plot the same graph as that given in the above mentioned reference but now we can discuss the variation in the dispersion curve for relativistic and weakly relativistic cases. As we decrease the value of $\eta$, i.e. we move towards the relativistic regime, the cutoff point (where the intersection of the relevant dotted line occurs) shifted to lower values of frequency or we can say that now the waves of lower values of frequency are allowed to propagate through the plasma.

Figure 1. Dispersion curves showing solutions for Langumir waves in relativistic plasma for different values of $\eta$ ($\eta =0.2$, $\eta =0.4$ and $\eta =0.6$).

Figure 2. Dispersion curves showing solutions for Langumir waves in weakly relativistic plasma for different values of $\eta$ ($\eta =2$, $\eta =2.5$ and $\eta =3$).

Figure 3. Dispersion curves showing solutions for Langumir waves in non-relativistic plasma for different values of $\eta$ ($\eta =16$, $\eta =18$ and $\eta =20$).

Figure 4. Dispersion curves showing solutions for Langumir waves in relativistic and weakly relativistic plasma for different values of $\eta$ ($\eta =0.2$ and $\eta =2$).

In figures 5 and 6, the dispersion curves for $R$-wave are shown where we can observe that in both of these figures (with different ratio of density to magnetic field) the curves are shifted to the lower value of frequency as the plasma environment becomes more relativistic. This shifting of the curves is due to the fact that the cyclotron frequency of electrons reduces as the relativistic effects increase. We also observe that the plasma becomes transparent for the relativistic case much earlier, i.e. at lower values of $k$, as compared with the weakly relativistic or non-relativistic cases. Moreover, as the value of ${\omega _{p}}/{\omega _{c}}$ increases, the density effects come in to play and the wave propagation shifts to higher values of frequency.

Figure 5. Dispersion curves showing solutions for $R$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=25$.

Similarly, the dispersion curves for the $L$-wave are shown in figures 7 and 8. The response of the $L$-wave to the relativistic effects and the ratio of density to magnetic field is the same as that of the $R$-wave. The plots presented in figures 9 and 10 show ${\omega ^2}/{c^2k^2}$ versus ${\omega }/{\omega _{ce}}$ for a fixed value of ${\omega ^2_{pe}}/{\omega ^2_{ce}}$, a standard way of representing the propagation region for our wave of interest. Since the wave cannot propagate below the cutoff frequency,this represents a no-propagation region. The propagation region is the one where the wave frequency becomes larger than the cutoff frequency. Now with an increase in the relativistic factor $\eta$ the cutoff point shifts to lower values of frequency, so the wave will start propagating at lower values of frequency which are not allowed in the non-relativistic case. This means that with the increase in the relativistic effects, the propagation region increases.

Figure 6. Dispersion curves showing solutions for $R$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=50$.

Figure 7. Dispersion curves showing solutions for $L$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=25$.

Figure 8. Dispersion curves showing solutions for $L$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=50$.

Figure 9. Dispersion curves showing the cutoffs of $R$-modes for relativistic plasma with ${\omega _{pe}^2}/{\omega _{ce}^2}=25$.

5. Conclusion

In this research work, we focus on relativistic plasmas which exist in many astrophysical (pulsars, quasars, active galactic nuclei, black holes, white dwarfs, neutron stars and radio galaxies) and laboratory (fusion experiment) environments. The increase in the effective mass not only depends on the the value of $\eta$ but also depends on plasma density. Our analysis for parallel propagating waves in various relativistic plasma environments is very useful for scientists working in both space science and the laboratory setting. On the basis of our calculations, we conclude that the propagation region for parallel propagating waves is enhanced for relativistic and weakly relativistic plasma as compared with the non-relativistic plasma which means that now the wave can propagate at lower frequencies that were not allowed for propagation in the non-relativistic regime. We also observe that a low-density and high-temperature (relativistic) plasma environment is more transparent for the parallel propagating waves as compared with a high-density and low-temperature (weakly relativistic and non-relativistic) plasma environment.

Figure 10. Dispersion curves showing the cutoffs of $L$-modes for relativistic plasma with ${\omega _{pe}^2}/{\omega _{ce}^2}=25$.

Acknowledgements

Editor Antoine C. Bret thanks the referees for their advice in evaluating this article.

Declaration of interest

The authors report no conflict of interest.

Data availability

The data that support the findings of this study are available within the article.

References

REFERENCES

Abbas, G., et al. 2012 Study of high frequency parallel propagating modes in a weakly magnetized relativistic degenerate electron plasma. Phys. Plasmas 19 (3), 032103.CrossRefGoogle Scholar
Ali, M., et al. 2019 Propagation of Bernstein waves in weakly relativistic pair ion plasma. Phys. Plasmas 26 (10), 102101.CrossRefGoogle Scholar
Asenjo, F., et al. 2009 Circularly polarized wave propagation in magnetofluid dynamics for relativistic electron-positron plasmas. Phys. Plasmas 16 (12), 122108.CrossRefGoogle Scholar
Bandaru, V., et al. 2019 Simulating the nonlinear interaction of relativistic electrons and tokamak plasma instabilities: implementation and validation of a fluid model. Phys. Rev. E 99 (6), 063317.CrossRefGoogle ScholarPubMed
Banerjee, S., et al. 2002 High harmonic generation in relativistic laser–plasma interaction. Phys. Plasmas 9 (5), 2393–2398.CrossRefGoogle Scholar
Beskin, V.S., et al. 1988 Theory of the radio emission of pulsars. AstroPhys. Space Sci. 146 (2), 205–281.CrossRefGoogle Scholar
Burden, R.L. & Faires, J.D. 1997 Numerical Analysis. Brooks/Cole.Google Scholar
Buti, B. 1963 Relativistic effects on plasma oscillations and two-stream instability. I. Phys. Fluids 6 (1), 89–99.CrossRefGoogle Scholar
Chabrier, G., et al. 2002 Dense astrophysical plasmas. J. Phys.: Condens. Matter 14 (40), 9133.Google Scholar
De Jonghe, J. & Keppens, R. 2020 A two-fluid analysis of waves in a warm ion–electron plasma. Phys. Plasmas 27 (12), 122107.CrossRefGoogle Scholar
Evans, G. 1993 Practical Numerical Integration. Wiley.Google Scholar
Georgiou, A. 1996 Dispersion relations for electron Bernstein waves in a relativistic plasma. Plasma Phys. Control. Fusion 38 (3), 347.CrossRefGoogle Scholar
Ghosh, B., et al. 2012 Relativistic effects on the modulational instability of electron plasma waves in quantum plasma. Pramana 78 (5), 779–790.CrossRefGoogle Scholar
Hazeltine, R.D. & Waelbroeck, F.L. 2018 The Framework of Plasma Physics. CRC Press.CrossRefGoogle Scholar
Horne, R.B., et al. 2005 Wave acceleration of electrons in the Van Allen radiation belts. Nature 437 (7056), 227–230.CrossRefGoogle ScholarPubMed
Keppens, R. & Goedbloed, H. 2019 A fresh look at waves in ion-electron plasmas. Front. Astron. Space Sci. 6, 11.CrossRefGoogle Scholar
Keppens, R., et al. 2019 Waves in a warm pair plasma: a relativistically complete two-fluid analysis. J. Plasma Phys. 85 (4).CrossRefGoogle Scholar
Khan, W., et al. 2020 a Parallel propagating waves in weakly magnetized relativistic electron plasma. IEEE Trans. Plasma Sci. 48 (9), 2996–3000.CrossRefGoogle Scholar
Khan, W., et al. 2020 b Electron cyclotron modes of Bernstein waves in different plasma environments. Plasma Res. Express 2 (1), 015004.CrossRefGoogle Scholar
Khan, W., et al. 2020 c Characteristics of ordinary mode in fully relativistic electron plasma. Plasma Phys. Control. Fusion 62 (5), 055016.CrossRefGoogle Scholar
Lazar, M. & Schlickeiser, R. 2006 Relativistic kinetic dispersion theory of linear parallel waves in magnetized plasmas with isotropic thermal distributions. New J. Phys. 8 (5), 66.CrossRefGoogle Scholar
Lerche, I. 1968 Quasilinear theory of resonant diffusion in a magneto-active, relativistic plasma. Phys. Fluid 11 (8), 1720–1727.CrossRefGoogle Scholar
Melrose, D.B. 2017 Coherent emission mechanisms in astrophysical plasmas. Rev. Mod. Plasma Phys. 1 (1), 1–81.CrossRefGoogle Scholar
Melrose, D.B. & Gedalin, M.E. 1999 Relativistic plasma emission and pulsar radio emission: a critique. Astrophys. J. 521 (1), 351.CrossRefGoogle Scholar
Montgomery, D.C. & Tidman, D.A. 1964 Plasma Kinetic Theory. McGraw-Hill.Google Scholar
Pelletier, G. & Marcowith, A. 1998 Nonlinear dynamics in the relativistic plasma of astrophysical high-energy sources. J. Astro phys. 502 (2), 598.CrossRefGoogle Scholar
Petropoulou, M., et al. 2019 Relativistic magnetic reconnection in electron–positron–proton plasmas: implications for jets of active galactic nuclei. AstroPhys. J. 880 (1), 37.CrossRefGoogle Scholar
Sazhin, S.S. 1987 An approximate theory of electromagnetic wave propagation in a weakly relativistic plasma. J. Plasma Phys. 37 (2), 209–230.CrossRefGoogle Scholar
Schlickeiser, R. 1998 Relativistic kinetic theory of plasma waves. Phys. Scr. 1998 (T75), 33.CrossRefGoogle Scholar
Yang, X.S. 2014 Introduction to Computational Mathematics. World Scientific Publishing Company.Google Scholar
Figure 0

Figure 1. Dispersion curves showing solutions for Langumir waves in relativistic plasma for different values of $\eta$ ($\eta =0.2$, $\eta =0.4$ and $\eta =0.6$).

Figure 1

Figure 2. Dispersion curves showing solutions for Langumir waves in weakly relativistic plasma for different values of $\eta$ ($\eta =2$, $\eta =2.5$ and $\eta =3$).

Figure 2

Figure 3. Dispersion curves showing solutions for Langumir waves in non-relativistic plasma for different values of $\eta$ ($\eta =16$, $\eta =18$ and $\eta =20$).

Figure 3

Figure 4. Dispersion curves showing solutions for Langumir waves in relativistic and weakly relativistic plasma for different values of $\eta$ ($\eta =0.2$ and $\eta =2$).

Figure 4

Figure 5. Dispersion curves showing solutions for $R$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=25$.

Figure 5

Figure 6. Dispersion curves showing solutions for $R$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=50$.

Figure 6

Figure 7. Dispersion curves showing solutions for $L$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=25$.

Figure 7

Figure 8. Dispersion curves showing solutions for $L$-mode in relativistic, weakly relativistic and non-relativistic plasma by taking ratio of ${\omega ^2_{pe}}/{\omega ^2_{ce}}=50$.

Figure 8

Figure 9. Dispersion curves showing the cutoffs of $R$-modes for relativistic plasma with ${\omega _{pe}^2}/{\omega _{ce}^2}=25$.

Figure 9

Figure 10. Dispersion curves showing the cutoffs of $L$-modes for relativistic plasma with ${\omega _{pe}^2}/{\omega _{ce}^2}=25$.