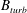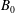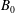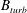1 Introduction
Magnetic fields are ubiquitous in the Universe. Examples include astrophysical accretion discs around young stars and active galactic nuclei, the interstellar and intergalactic medium and even the early Universe when the first stars and galaxies formed.
The turbulent dynamo mechanism is believed to be the main cause of cosmic magnetism (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005). Magnetic fields are amplified exponentially via the turbulent dynamo, leading to dynamically important magnetic forces and energies on relatively short time scales. The amplification of the magnetic field arises from sequences of ‘stretching, twisting and folding’ of the field, until the magnetic field lines are so tightly packed that the magnetic energy density becomes comparable to the kinetic energy density provided by turbulent motions.
Dynamo action ranges from the Earth and the Sun (Cattaneo & Hughes Reference Cattaneo and Hughes2001), over the interstellar medium to whole galaxies (Beck et al. Reference Beck, Brandenburg, Moss, Shukurov and Sokoloff1996; Beck Reference Beck2016). The turbulent dynamo is important for the formation of the large-scale structure of the Universe (Ryu et al. Reference Ryu, Kang, Cho and Das2008; Miniati & Bell Reference Miniati and Bell2011; Iapichino & Brüggen Reference Iapichino and Brüggen2012; Vazza et al. Reference Vazza, Brüggen, Gheller and Wang2014; Miniati & Beresnyak Reference Miniati and Beresnyak2015; Beresnyak & Miniati Reference Beresnyak and Miniati2016), in clusters of galaxies (Subramanian, Shukurov & Haugen Reference Subramanian, Shukurov and Haugen2006) and in the formation of the first cosmological objects in dark matter haloes (Schleicher et al. Reference Schleicher, Banerjee, Sur, Arshakian, Klessen, Beck and Spaans2010). It determines the growth of magnetic energy in solar convection (Cattaneo & Hughes Reference Cattaneo and Hughes2001; Pietarila Graham, Cameron & Schüssler Reference Pietarila Graham, Cameron and Schüssler2010; Moll et al. Reference Moll, Pietarila Graham, Pratt, Cameron, Müller and Schüssler2011), in the interior of planets (Roberts & Glatzmaier Reference Roberts and Glatzmaier2000) and is relevant for liquid metal experiments on Earth (Monchaux et al. Reference Monchaux, Berhanu, Bourgoin, Moulin, Odier, Pinton, Volk, Fauve, Mordant and Pétrélis2007). It may further explain the far-infrared–radio correlation in spiral galaxies (Schleicher & Beck Reference Schleicher and Beck2013). After the turbulent dynamo has amplified tiny seeds of the magnetic field, which can be generated during inflation, the electroweak or the quantum chromodynamics (QCD) phase transition (Grasso & Rubinstein Reference Grasso and Rubinstein2001), the large-scale dynamo kicks in and generates the large-scale magnetic fields observed in planets, stars and galaxies today (Beck et al. Reference Beck, Brandenburg, Moss, Shukurov and Sokoloff1996; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005).
One of the most important distinctions that we have to make when considering turbulent gases, fluids and plasmas, is the level of compressibility of the medium. For instance, in the Earth and the Sun, the dynamo is driven by subsonic, nearly incompressible flows. By contrast, interstellar clouds and galaxies are dominated by highly compressible turbulence (Elmegreen & Scalo Reference Elmegreen and Scalo2004; Mac Low & Klessen Reference Mac Low and Klessen2004; McKee & Ostriker Reference McKee and Ostriker2007; Hennebelle & Falgarone Reference Hennebelle and Falgarone2012; Padoan et al.
Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014). Indeed, the gas densities in the interstellar medium range from
![]() ${\lesssim}1$
particle per
${\lesssim}1$
particle per
![]() $\text{cm}^{3}$
(the average gas density in a Milky Way-type galaxy; see Ferrière Reference Ferrière2001) to
$\text{cm}^{3}$
(the average gas density in a Milky Way-type galaxy; see Ferrière Reference Ferrière2001) to
![]() ${\gtrsim}10^{10}~\text{cm}^{-3}$
(where the gas becomes optically thick and proceeds to the formation of a star).
${\gtrsim}10^{10}~\text{cm}^{-3}$
(where the gas becomes optically thick and proceeds to the formation of a star).
Numerical studies of non-driven turbulence demonstrated that supersonic turbulence decays quickly, in approximately a crossing time (Scalo & Pumphrey Reference Scalo and Pumphrey1982; Mac Low et al. Reference Mac Low, Klessen, Burkert and Smith1998; Stone, Ostriker & Gammie Reference Stone, Ostriker and Gammie1998; Mac Low Reference Mac Low1999). Since we observe highly compressible interstellar turbulence, that turbulence must be driven by some physical forcing mechanisms. Those mechanisms include supernova explosions, ionizing shells from high-mass stellar feedback (McKee Reference McKee1989; Balsara et al. Reference Balsara, Kim, Mac Low and Mathews2004; de Avillez & Breitschwerdt Reference de Avillez and Breitschwerdt2005; Krumholz, Matzner & McKee Reference Krumholz, Matzner and McKee2006; Breitschwerdt et al. Reference Breitschwerdt, de Avillez, Fuchs and Dettbarn2009; Gritschneder et al. Reference Gritschneder, Naab, Walch, Burkert and Heitsch2009; Peters et al. Reference Peters, Banerjee, Klessen, Mac Low, Galván-Madrid and Keto2010, Reference Peters, Banerjee, Klessen and Mac Low2011; Goldbaum et al. Reference Goldbaum, Krumholz, Matzner and McKee2011; Lee, Murray & Rahman Reference Lee, Murray and Rahman2012), gravitational collapse and accretion of material (Hoyle Reference Hoyle1953; Vazquez-Semadeni, Canto & Lizano Reference Vazquez-Semadeni, Canto and Lizano1998; Klessen & Hennebelle Reference Klessen and Hennebelle2010; Elmegreen & Burkert Reference Elmegreen and Burkert2010; Vázquez-Semadeni et al. Reference Vázquez-Semadeni, Colín, Gómez, Ballesteros-Paredes and Watson2010; Federrath et al. Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011b ; Robertson & Goldreich Reference Robertson and Goldreich2012) and galactic spiral-arm compression and cloud–cloud collisions (Dobbs & Bonnell Reference Dobbs and Bonnell2008; Dobbs et al. Reference Dobbs, Glover, Clark and Klessen2008; Tasker & Tan Reference Tasker and Tan2009; Benincasa et al. Reference Benincasa, Tasker, Pudritz and Wadsley2013), as well as magnetorotational instability (Piontek & Ostriker Reference Piontek and Ostriker2004, Reference Piontek and Ostriker2007; Tamburro et al. Reference Tamburro, Rix, Leroy, Low, Walter, Kennicutt, Brinks and de Blok2009). Jets and outflows from young stellar objects (Norman & Silk Reference Norman and Silk1980; Banerjee, Klessen & Fendt Reference Banerjee, Klessen and Fendt2007; Nakamura & Li Reference Nakamura and Li2008; Cunningham et al. Reference Cunningham, Frank, Carroll, Blackman and Quillen2009; Carroll, Frank & Blackman Reference Carroll, Frank and Blackman2010; Wang et al. Reference Wang, Li, Abel and Nakamura2010) and active galactic nuclei (Mukherjee et al. Reference Mukherjee, Bicknell, Sutherland and Wagner2016) also drive turbulence. Turbulence in high-redshift galaxies and their low-redshift analogues may be driven by feedback (Green et al. Reference Green, Glazebrook, McGregor, Abraham, Poole, Damjanov, McCarthy, Colless and Sharp2010; Fisher et al. Reference Fisher, Glazebrook, Bolatto, Obreschkow, Mentuch Cooper, Wisnioski, Bassett, Abraham, Damjanov and Green2014). Discussions and comparisons of turbulence driving mechanisms are published in Mac Low & Klessen (Reference Mac Low and Klessen2004), Elmegreen (Reference Elmegreen, Andersen, Bland-Hawthorn and Nordström2009) and Federrath et al. (Reference Federrath, Rathborne, Longmore, Kruijssen, Bally, Contreras, Crocker, Garay, Jackson and Testi2016a ).
Most importantly, the majority of turbulence drivers (e.g. supernova explosions, high-mass stellar winds and accretion) are expected to drive compressible modes, so we refer to these as ‘compressive drivers’. On the other hand, solenoidal modes can be generated directly by shear (Federrath et al. Reference Federrath, Rathborne, Longmore, Kruijssen, Bally, Contreras, Crocker, Garay, Jackson and Testi2016b ) and the magnetorotational instability (MRI) (so we call them ‘solenoidal drivers’), and indirectly by nonlinear interactions of multiple colliding shock fronts (Vishniac Reference Vishniac1994; Sun & Takayama Reference Sun and Takayama2003; Kritsuk et al. Reference Kritsuk, Norman, Padoan and Wagner2007; Federrath et al. Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010), baroclinicity (Padoan et al. Reference Padoan, Pan, Haugbølle and Nordlund2016), rotation and shear (Del Sordo & Brandenburg Reference Del Sordo and Brandenburg2011) as well as viscosity (Mee & Brandenburg Reference Mee and Brandenburg2006; Federrath et al. Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a ). Thus, turbulence driven by purely compressive drivers can still contain up to half of its kinetic power in solenoidal modes (Federrath et al. Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010, Figure 14).
In order to understand the dependence of the dynamo on the compressibility of the plasma, we present in § 2 a systematic study in which the turbulent driving and Mach number are varied, covering the subsonic, nearly incompressible regime as well as the highly compressible, supersonic regime of turbulence. We determine the growth rate and saturation level of the magnetic field in both regimes. In § 3 we determine the dependence of the compressible turbulent dynamo on the magnetic Prandtl number and the kinematic Reynolds number.
Many astrophysical systems are characterised by weak or strong magnetic guide fields, i.e. fields that have an ordered mean component along a specified direction. This is in contrast to the turbulent dynamo, where primarily the turbulent un-ordered magnetic field component is amplified on small scales. In order to measure and understand magnetic field amplification in the presence of a strong guide field, we present new simulations in § 4, where we systematically measure the strength of the turbulent magnetic field component as a function of increasing magnetic guide field.
Finally, in § 5 we discuss the implications of magnetic fields for astrophysical accretion discs, the structure of the interstellar medium and for star formation.
2 The Mach number dependence of the turbulent dynamo
Here we investigate fundamental properties of the turbulent dynamo – its growth rate and saturation level – in simulations with extremely different driving of the turbulence (solenoidal versus compressive) and with a range of Mach numbers from
![]() ${\mathcal{M}}=0.02$
to
${\mathcal{M}}=0.02$
to
![]() $20$
. Some of the results in this section are published in Federrath et al. (Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
). While these simulations are highly idealised, they serve as a systematic numerical experiment in which the driving and Mach number are controlled. Turbulent astrophysical systems can often be characterised by a few fundamental numbers that cover the basic physical behaviour. For example, the turbulence in astrophysical accretion discs around young stars is subsonic (
$20$
. Some of the results in this section are published in Federrath et al. (Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
). While these simulations are highly idealised, they serve as a systematic numerical experiment in which the driving and Mach number are controlled. Turbulent astrophysical systems can often be characterised by a few fundamental numbers that cover the basic physical behaviour. For example, the turbulence in astrophysical accretion discs around young stars is subsonic (
![]() ${\mathcal{M}}<1$
) and is primarily driven by shear or magnetorotational instability, which drive solenoidal motions (solenoidal driving). By contrast, molecular cloud turbulence is highly compressible and supersonic (
${\mathcal{M}}<1$
) and is primarily driven by shear or magnetorotational instability, which drive solenoidal motions (solenoidal driving). By contrast, molecular cloud turbulence is highly compressible and supersonic (
![]() ${\mathcal{M}}>1$
), and is driven by a range of physical processes, most of which induce compression (compressive driving), such as supernova explosions, expanding radiation fronts from high-mass stellar feedback and/or galactic spiral shocks. For a review of potential drivers of the turbulence in galaxies and the interstellar medium, please see the articles by Elmegreen (Reference Elmegreen, Andersen, Bland-Hawthorn and Nordström2009), Federrath et al. (Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010), Federrath & Klessen (Reference Federrath and Klessen2012) and Padoan et al. (Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014).
${\mathcal{M}}>1$
), and is driven by a range of physical processes, most of which induce compression (compressive driving), such as supernova explosions, expanding radiation fronts from high-mass stellar feedback and/or galactic spiral shocks. For a review of potential drivers of the turbulence in galaxies and the interstellar medium, please see the articles by Elmegreen (Reference Elmegreen, Andersen, Bland-Hawthorn and Nordström2009), Federrath et al. (Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010), Federrath & Klessen (Reference Federrath and Klessen2012) and Padoan et al. (Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014).
2.1 Background and open questions
Most studies of the turbulent dynamo concentrate on incompressible plasmas, with only few studies approaching the effects of compressibility. For example, Haugen, Brandenburg & Mee (Reference Haugen, Brandenburg and Mee2004b
) obtained critical Reynolds numbers for dynamo action, but did not investigate growth rates or saturation levels, and only studied Mach numbers in the range
![]() $0.1\leqslant {\mathcal{M}}\leqslant 2.6$
. The energy released by e.g. supernova explosions, however, drives interstellar and galactic turbulence with Mach numbers of 10–100 (Mac Low & Klessen Reference Mac Low and Klessen2004). Thus, much higher Mach numbers have to be investigated in order to understand dynamo action in interstellar clouds. It is furthermore tempting to associate such supernova blast waves with compressive driving of turbulence (Mee & Brandenburg Reference Mee and Brandenburg2006; Schmidt, Federrath & Klessen Reference Schmidt, Federrath and Klessen2008; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010). Mee & Brandenburg (Reference Mee and Brandenburg2006) concluded that it is very hard to excite the turbulent dynamo with this curl-free driving, because it does not directly inject vorticity,
$0.1\leqslant {\mathcal{M}}\leqslant 2.6$
. The energy released by e.g. supernova explosions, however, drives interstellar and galactic turbulence with Mach numbers of 10–100 (Mac Low & Klessen Reference Mac Low and Klessen2004). Thus, much higher Mach numbers have to be investigated in order to understand dynamo action in interstellar clouds. It is furthermore tempting to associate such supernova blast waves with compressive driving of turbulence (Mee & Brandenburg Reference Mee and Brandenburg2006; Schmidt, Federrath & Klessen Reference Schmidt, Federrath and Klessen2008; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010). Mee & Brandenburg (Reference Mee and Brandenburg2006) concluded that it is very hard to excite the turbulent dynamo with this curl-free driving, because it does not directly inject vorticity,
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{u}$
.
$\unicode[STIX]{x1D735}\times \boldsymbol{u}$
.
Here we show that the turbulent dynamo can be driven by curl-free driving mechanisms, and we quantify the amplification as a function of compressibility of the plasma. The main questions addressed are: how does the turbulent dynamo depend on the Mach number and driving of the turbulence? What is the field geometry and amplification mechanism? What are the growth rates and saturation levels in the subsonic and supersonic regime?
2.2 Methods
2.2.1 Magnetohydrodynamical equations
We use a modified version of the FLASH code (Fryxell et al. Reference Fryxell, Olson, Ricker, Timmes, Zingale, Lamb, MacNeice, Rosner, Truran and Tufo2000; Dubey et al. Reference Dubey, Fisher, Graziani, Jordan, Lamb, Reid, Rich, Sheeler, Townsley, Weide, Pogorelov, Audit and Zank2008) to solve the three-dimensional (3-D), compressible, magnetohydrodynamical (MHD) equations on uniform, periodic grids, including viscous and resistive dissipation terms,
Here,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\boldsymbol{u}$
,
$\boldsymbol{u}$
,
![]() $p_{tot}=p_{th}+(1/8\unicode[STIX]{x03C0})|\boldsymbol{B}|^{2}$
,
$p_{tot}=p_{th}+(1/8\unicode[STIX]{x03C0})|\boldsymbol{B}|^{2}$
,
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $e=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}_{int}+(1/2)\unicode[STIX]{x1D70C}|\boldsymbol{u}|^{2}+(1/8\unicode[STIX]{x03C0})|\boldsymbol{B}|^{2}$
denote the gas density, velocity, pressure (thermal plus magnetic), magnetic field and energy density (internal plus kinetic plus magnetic), respectively. Physical shear viscosity is included with the traceless rate of strain tensor,
$e=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D716}_{int}+(1/2)\unicode[STIX]{x1D70C}|\boldsymbol{u}|^{2}+(1/8\unicode[STIX]{x03C0})|\boldsymbol{B}|^{2}$
denote the gas density, velocity, pressure (thermal plus magnetic), magnetic field and energy density (internal plus kinetic plus magnetic), respectively. Physical shear viscosity is included with the traceless rate of strain tensor,
![]() ${\mathcal{S}}_{ij}=(1/2)(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})-(1/3)\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
in the momentum equation (2.2), and controlled by the kinematic viscosity (
${\mathcal{S}}_{ij}=(1/2)(\unicode[STIX]{x2202}_{i}u_{j}+\unicode[STIX]{x2202}_{j}u_{i})-(1/3)\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}$
in the momentum equation (2.2), and controlled by the kinematic viscosity (
![]() $\unicode[STIX]{x1D708}$
). Physical diffusion of
$\unicode[STIX]{x1D708}$
). Physical diffusion of
![]() $\boldsymbol{B}$
is controlled by the magnetic diffusivity
$\boldsymbol{B}$
is controlled by the magnetic diffusivity
![]() $\unicode[STIX]{x1D702}=1/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E})$
(the inverse of the electrical conductivity
$\unicode[STIX]{x1D702}=1/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E})$
(the inverse of the electrical conductivity
![]() $\unicode[STIX]{x1D70E}$
) in the induction equation (2.4). The MHD equations are closed with an isothermal equation of state,
$\unicode[STIX]{x1D70E}$
) in the induction equation (2.4). The MHD equations are closed with an isothermal equation of state,
![]() $p_{th}=c_{s}^{2}\unicode[STIX]{x1D70C}$
, where
$p_{th}=c_{s}^{2}\unicode[STIX]{x1D70C}$
, where
![]() $c_{s}=\text{const.}$
is the sound speed.
$c_{s}=\text{const.}$
is the sound speed.
We note that (2.2) and (2.3) only contain the shear viscosity
![]() $\unicode[STIX]{x1D708}$
, while the bulk viscosity is assumed to be zero. For monatomic ideal gases, the bulk viscosity
$\unicode[STIX]{x1D708}$
, while the bulk viscosity is assumed to be zero. For monatomic ideal gases, the bulk viscosity
![]() $\unicode[STIX]{x1D709}$
is indeed identically zero, which can be derived from kinetic theory (Mihalas & Mihalas Reference Mihalas and Mihalas1984). For polyatomic molecules, this does not need to be the case, but
$\unicode[STIX]{x1D709}$
is indeed identically zero, which can be derived from kinetic theory (Mihalas & Mihalas Reference Mihalas and Mihalas1984). For polyatomic molecules, this does not need to be the case, but
![]() $\unicode[STIX]{x1D709}\neq 0$
only, if a relaxation process takes place that is of the same order or slower than a typical fluid time scale (Mihalas & Mihalas Reference Mihalas and Mihalas1984). The value of
$\unicode[STIX]{x1D709}\neq 0$
only, if a relaxation process takes place that is of the same order or slower than a typical fluid time scale (Mihalas & Mihalas Reference Mihalas and Mihalas1984). The value of
![]() $\unicode[STIX]{x1D709}$
strongly depends on the composition of the polyatomic gas and measurements of
$\unicode[STIX]{x1D709}$
strongly depends on the composition of the polyatomic gas and measurements of
![]() $\unicode[STIX]{x1D709}$
from different experiments give different results (Tisza Reference Tisza1942). For simplicity, we set the bulk viscosity
$\unicode[STIX]{x1D709}$
from different experiments give different results (Tisza Reference Tisza1942). For simplicity, we set the bulk viscosity
![]() $\unicode[STIX]{x1D709}=0$
and only consider the well-understood shear viscosity
$\unicode[STIX]{x1D709}=0$
and only consider the well-understood shear viscosity
![]() $\unicode[STIX]{x1D708}$
. We further note that using an equation of state for the gas that relates pressure with density and temperature (which is the standard approach in fluid dynamics) implies
$\unicode[STIX]{x1D708}$
. We further note that using an equation of state for the gas that relates pressure with density and temperature (which is the standard approach in fluid dynamics) implies
![]() $\unicode[STIX]{x1D709}=0$
(Truesdell Reference Truesdell1952).
$\unicode[STIX]{x1D709}=0$
(Truesdell Reference Truesdell1952).
2.2.2 Turbulence driving
In order to drive turbulence with a target Mach number, we apply the driving field
![]() $\boldsymbol{F}$
as a source term in the momentum equation (2.2). The driving field is constructed with a stochastic Ornstein–Uhlenbeck (OU) process (Eswaran & Pope Reference Eswaran and Pope1988; Schmidt et al.
Reference Schmidt, Federrath, Hupp, Kern and Niemeyer2009; Price & Federrath Reference Price and Federrath2010), implemented by Federrath et al. (Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010) in the public version of the FLASH code (https://www.flash.uchicago.edu/site/flashcode/). The OU process yields a driving pattern that varies smoothly in space and time with an auto-correlation time equal to the eddy-turnover time (also called turbulent box-crossing time),
$\boldsymbol{F}$
as a source term in the momentum equation (2.2). The driving field is constructed with a stochastic Ornstein–Uhlenbeck (OU) process (Eswaran & Pope Reference Eswaran and Pope1988; Schmidt et al.
Reference Schmidt, Federrath, Hupp, Kern and Niemeyer2009; Price & Federrath Reference Price and Federrath2010), implemented by Federrath et al. (Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010) in the public version of the FLASH code (https://www.flash.uchicago.edu/site/flashcode/). The OU process yields a driving pattern that varies smoothly in space and time with an auto-correlation time equal to the eddy-turnover time (also called turbulent box-crossing time),
![]() $t_{ed}=L/(2{\mathcal{M}}c_{s})$
on the largest scales (
$t_{ed}=L/(2{\mathcal{M}}c_{s})$
on the largest scales (
![]() $L/2$
) in the periodic simulation domain of side length
$L/2$
) in the periodic simulation domain of side length
![]() $L$
. The turbulent sonic Mach number is defined as
$L$
. The turbulent sonic Mach number is defined as
![]() ${\mathcal{M}}=u_{turb}/c_{s}$
, which is the ratio of the turbulent velocity dispersion
${\mathcal{M}}=u_{turb}/c_{s}$
, which is the ratio of the turbulent velocity dispersion
![]() $u_{turb}$
on scale
$u_{turb}$
on scale
![]() $L/2$
and the sound speed
$L/2$
and the sound speed
![]() $c_{s}$
. The driving is constructed in Fourier space such that the kinetic energy is injected at the smallest wavenumbers,
$c_{s}$
. The driving is constructed in Fourier space such that the kinetic energy is injected at the smallest wavenumbers,
![]() $1<|\boldsymbol{k}|L/2\unicode[STIX]{x03C0}<3$
. The peak of energy injection is on scale
$1<|\boldsymbol{k}|L/2\unicode[STIX]{x03C0}<3$
. The peak of energy injection is on scale
![]() $L/2$
, i.e.
$L/2$
, i.e.
![]() $k=2$
, and falls off parabolically towards smaller and higher wavenumbers such that the driving power reaches zero exactly at
$k=2$
, and falls off parabolically towards smaller and higher wavenumbers such that the driving power reaches zero exactly at
![]() $k=1$
and
$k=1$
and
![]() $k=3$
. This procedure limits the direct effect of the driving to a narrow wavenumber band (
$k=3$
. This procedure limits the direct effect of the driving to a narrow wavenumber band (
![]() $1<|\boldsymbol{k}|L/2\unicode[STIX]{x03C0}<3$
) and allows the turbulence to develop self-consistently on smaller scales (
$1<|\boldsymbol{k}|L/2\unicode[STIX]{x03C0}<3$
) and allows the turbulence to develop self-consistently on smaller scales (
![]() $k\geqslant 3$
).
$k\geqslant 3$
).
By applying a projection in Fourier space, we can decompose the driving field into its solenoidal and compressive parts. In index notation, the projection operator reads
where
![]() ${\mathcal{P}}_{ij}^{\bot }$
and
${\mathcal{P}}_{ij}^{\bot }$
and
![]() ${\mathcal{P}}_{ij}^{\Vert }$
are the solenoidal and compressive projection operators, respectively. This yields a ratio of compressive driving power
${\mathcal{P}}_{ij}^{\Vert }$
are the solenoidal and compressive projection operators, respectively. This yields a ratio of compressive driving power
![]() $F_{comp}$
to total driving power
$F_{comp}$
to total driving power
![]() $F_{tot}$
as a function of the parameter
$F_{tot}$
as a function of the parameter
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
The projection operation allows us to construct a solenoidal (divergence-free) driving field (
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}=0$
) or a compressive (curl-free) driving field (
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{F}=0$
) or a compressive (curl-free) driving field (
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{F}=0$
) by setting
$\unicode[STIX]{x1D735}\times \boldsymbol{F}=0$
) by setting
![]() $\unicode[STIX]{x1D701}=1$
(solenoidal) or
$\unicode[STIX]{x1D701}=1$
(solenoidal) or
![]() $\unicode[STIX]{x1D701}=0$
(compressive). Mixed driving ratios are obtained by picking values in the range
$\unicode[STIX]{x1D701}=0$
(compressive). Mixed driving ratios are obtained by picking values in the range
![]() $1<\unicode[STIX]{x1D701}<0$
. Setting
$1<\unicode[STIX]{x1D701}<0$
. Setting
![]() $\unicode[STIX]{x1D701}=1/2$
yields a ‘natural mixture’, i.e. a driving field with
$\unicode[STIX]{x1D701}=1/2$
yields a ‘natural mixture’, i.e. a driving field with
![]() $F_{comp}/F_{tot}=1/3$
. The latter is equivalent to the result of randomly chosen driving modes in three dimensions, where on average one spatial dimension is occupied by longitudinal (compressive) modes and two spatial dimensions are occupied by transverse (solenoidal) modes (Federrath, Klessen & Schmidt Reference Federrath, Klessen and Schmidt2008).
$F_{comp}/F_{tot}=1/3$
. The latter is equivalent to the result of randomly chosen driving modes in three dimensions, where on average one spatial dimension is occupied by longitudinal (compressive) modes and two spatial dimensions are occupied by transverse (solenoidal) modes (Federrath, Klessen & Schmidt Reference Federrath, Klessen and Schmidt2008).
2.2.3 Initial conditions and numerical methods
We start our numerical experiments by setting
![]() $L=1.24\times 10^{19}~\text{cm}$
, zero initial velocities
$L=1.24\times 10^{19}~\text{cm}$
, zero initial velocities
![]() $\boldsymbol{u}_{0}=0$
, uniform density
$\boldsymbol{u}_{0}=0$
, uniform density
![]() $\unicode[STIX]{x1D70C}_{0}=1.93\times 10^{-21}~\text{g}~\text{cm}^{-3}$
,
$\unicode[STIX]{x1D70C}_{0}=1.93\times 10^{-21}~\text{g}~\text{cm}^{-3}$
,
![]() $c_{s}=2\times 10^{4}~\text{cm}~\text{s}^{-1}$
and
$c_{s}=2\times 10^{4}~\text{cm}~\text{s}^{-1}$
and
![]() $\boldsymbol{B}=(0,0,B_{0z})$
with
$\boldsymbol{B}=(0,0,B_{0z})$
with
![]() $B_{0z}=4.4\times 10^{-16}~\text{G}$
in the
$B_{0z}=4.4\times 10^{-16}~\text{G}$
in the
![]() $z$
-direction, corresponding to an extremely large initial plasma
$z$
-direction, corresponding to an extremely large initial plasma
![]() $\unicode[STIX]{x1D6FD}=p_{th}/p_{m}=10^{20}$
. These values are motivated by dynamo studies of primordial clouds (Schleicher et al.
Reference Schleicher, Banerjee, Sur, Arshakian, Klessen, Beck and Spaans2010; Sur et al.
Reference Sur, Schleicher, Banerjee, Federrath and Klessen2010; Federrath et al.
Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011b
; Sur et al.
Reference Sur, Federrath, Schleicher, Banerjee and Klessen2012), but in the following, we scale all quantities to dimensionless units to address fundamental questions of magnetic field amplification in compressible plasmas. The physics of these turbulent systems is fully determined by the dimensionless
$\unicode[STIX]{x1D6FD}=p_{th}/p_{m}=10^{20}$
. These values are motivated by dynamo studies of primordial clouds (Schleicher et al.
Reference Schleicher, Banerjee, Sur, Arshakian, Klessen, Beck and Spaans2010; Sur et al.
Reference Sur, Schleicher, Banerjee, Federrath and Klessen2010; Federrath et al.
Reference Federrath, Sur, Schleicher, Banerjee and Klessen2011b
; Sur et al.
Reference Sur, Federrath, Schleicher, Banerjee and Klessen2012), but in the following, we scale all quantities to dimensionless units to address fundamental questions of magnetic field amplification in compressible plasmas. The physics of these turbulent systems is fully determined by the dimensionless
![]() ${\mathcal{M}}$
and plasma
${\mathcal{M}}$
and plasma
![]() $\unicode[STIX]{x1D6FD}$
, as well as the driving parameter
$\unicode[STIX]{x1D6FD}$
, as well as the driving parameter
![]() $\unicode[STIX]{x1D701}$
(solenoidal versus compressive). The actual plasma densities, velocities and magnetic fields can be scaled to astrophysical systems that are described by the same set of basic dimensionless numbers (
$\unicode[STIX]{x1D701}$
(solenoidal versus compressive). The actual plasma densities, velocities and magnetic fields can be scaled to astrophysical systems that are described by the same set of basic dimensionless numbers (
![]() ${\mathcal{M}}$
,
${\mathcal{M}}$
,
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D701}$
).
$\unicode[STIX]{x1D701}$
).
For most of the simulations, we set the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
and the magnetic diffusivity
$\unicode[STIX]{x1D708}$
and the magnetic diffusivity
![]() $\unicode[STIX]{x1D702}$
to zero, and thus solve the ideal MHD equations. In this case, the dissipation of kinetic and magnetic energy is caused by the discretisation of the MHD equations. However, we do not add artificial viscosity. We use Riemann solvers, which capture shocks well in the absence of artificial viscosity. In addition to the ideal MHD simulations, we also solve the full, non-ideal MHD equations (2.1)–(2.5) for four representative models to show that our results are physical and robust against changes in the numerical scheme. For the ideal MHD simulations, we use the positive–definite, split HLL3R Riemann scheme (Waagan, Federrath & Klingenberg Reference Waagan, Federrath and Klingenberg2011) in FLASH v2.5, while our non-ideal MHD simulations were performed with the un-split staggered-mesh scheme in FLASH v4 (Lee & Deane Reference Lee and Deane2009), which uses a third-order reconstruction, constrained transport to maintain
$\unicode[STIX]{x1D702}$
to zero, and thus solve the ideal MHD equations. In this case, the dissipation of kinetic and magnetic energy is caused by the discretisation of the MHD equations. However, we do not add artificial viscosity. We use Riemann solvers, which capture shocks well in the absence of artificial viscosity. In addition to the ideal MHD simulations, we also solve the full, non-ideal MHD equations (2.1)–(2.5) for four representative models to show that our results are physical and robust against changes in the numerical scheme. For the ideal MHD simulations, we use the positive–definite, split HLL3R Riemann scheme (Waagan, Federrath & Klingenberg Reference Waagan, Federrath and Klingenberg2011) in FLASH v2.5, while our non-ideal MHD simulations were performed with the un-split staggered-mesh scheme in FLASH v4 (Lee & Deane Reference Lee and Deane2009), which uses a third-order reconstruction, constrained transport to maintain
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
to machine precision, and the HLLD Riemann solver (Miyoshi & Kusano Reference Miyoshi and Kusano2005). We run simulations with
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
to machine precision, and the HLLD Riemann solver (Miyoshi & Kusano Reference Miyoshi and Kusano2005). We run simulations with
![]() $128^{3}$
,
$128^{3}$
,
![]() $256^{3}$
, and
$256^{3}$
, and
![]() $512^{3}$
grid cells, in order to test numerical convergence of our results.
$512^{3}$
grid cells, in order to test numerical convergence of our results.
2.3 Results
2.3.1 Time evolution
The turbulence is fully developed after an initial transient phase that lasts for
![]() $2\,t_{ed}$
(e.g. Federrath, Klessen & Schmidt Reference Federrath, Klessen and Schmidt2009; Kitsionas et al.
Reference Kitsionas, Federrath, Klessen, Schmidt, Price, Dursi, Gritschneder, Walch, Piontek and Kim2009; Price & Federrath Reference Price and Federrath2010), and the Mach number reaches its target value, fluctuating at a 10 % level. Figure 1 shows the time evolution of
$2\,t_{ed}$
(e.g. Federrath, Klessen & Schmidt Reference Federrath, Klessen and Schmidt2009; Kitsionas et al.
Reference Kitsionas, Federrath, Klessen, Schmidt, Price, Dursi, Gritschneder, Walch, Piontek and Kim2009; Price & Federrath Reference Price and Federrath2010), and the Mach number reaches its target value, fluctuating at a 10 % level. Figure 1 shows the time evolution of
![]() ${\mathcal{M}}$
in all runs with solenoidal and compressive driving of the turbulence. Some simulations had to be run for a few hundred crossing times in order to reach saturation of the magnetic field. This is the case in all the compressively driven simulations, which – as we will see below – have significantly lower dynamo growth rates than in the case of solenoidal driving. Interesting to note is the drop in
${\mathcal{M}}$
in all runs with solenoidal and compressive driving of the turbulence. Some simulations had to be run for a few hundred crossing times in order to reach saturation of the magnetic field. This is the case in all the compressively driven simulations, which – as we will see below – have significantly lower dynamo growth rates than in the case of solenoidal driving. Interesting to note is the drop in
![]() ${\mathcal{M}}$
for the solenoidally driven runs with
${\mathcal{M}}$
for the solenoidally driven runs with
![]() ${\mathcal{M}}\lesssim 1$
towards late times,
${\mathcal{M}}\lesssim 1$
towards late times,
![]() $t\gtrsim 50\,t_{ed}$
. This slight drop in Mach number indicates that the magnetic field has reached very high saturation levels, such that the back reaction of the magnetic field via the Lorentz force has become significant in these models. However, the magnetic field has little dynamical impact on the turbulent flow in all supersonic runs and in all runs with compressive driving. Although the kinematics of the turbulent flow is not strongly affected in those cases, the structure and fragmentation of the gas is still influenced by the presence of a turbulent magnetic field (Hennebelle & Teyssier Reference Hennebelle and Teyssier2008; Federrath & Klessen Reference Federrath and Klessen2012; Padoan et al.
Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014).
$t\gtrsim 50\,t_{ed}$
. This slight drop in Mach number indicates that the magnetic field has reached very high saturation levels, such that the back reaction of the magnetic field via the Lorentz force has become significant in these models. However, the magnetic field has little dynamical impact on the turbulent flow in all supersonic runs and in all runs with compressive driving. Although the kinematics of the turbulent flow is not strongly affected in those cases, the structure and fragmentation of the gas is still influenced by the presence of a turbulent magnetic field (Hennebelle & Teyssier Reference Hennebelle and Teyssier2008; Federrath & Klessen Reference Federrath and Klessen2012; Padoan et al.
Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014).
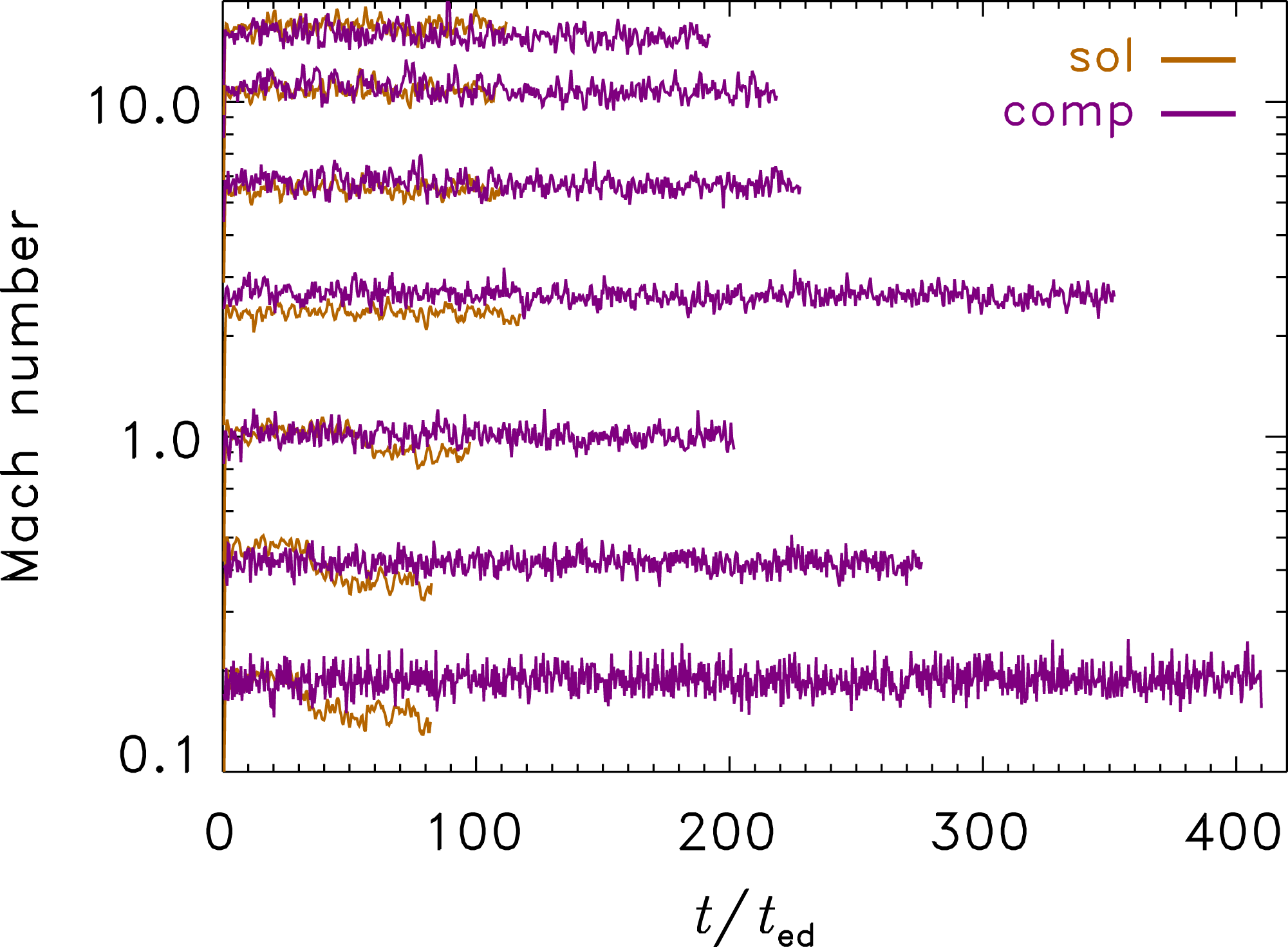
Figure 1. Turbulent sonic Mach number (
![]() ${\mathcal{M}}$
) as a function of the turbulent crossing time (
${\mathcal{M}}$
) as a function of the turbulent crossing time (
![]() $t/t_{ed}$
) for all runs with solenoidal (sol) and compressive (comp) driving. These simulations cover compressible plasmas from subsonic turbulence (
$t/t_{ed}$
) for all runs with solenoidal (sol) and compressive (comp) driving. These simulations cover compressible plasmas from subsonic turbulence (
![]() ${\mathcal{M}}<1$
) up into the highly compressible, supersonic regime (
${\mathcal{M}}<1$
) up into the highly compressible, supersonic regime (
![]() ${\mathcal{M}}>1$
).
${\mathcal{M}}>1$
).
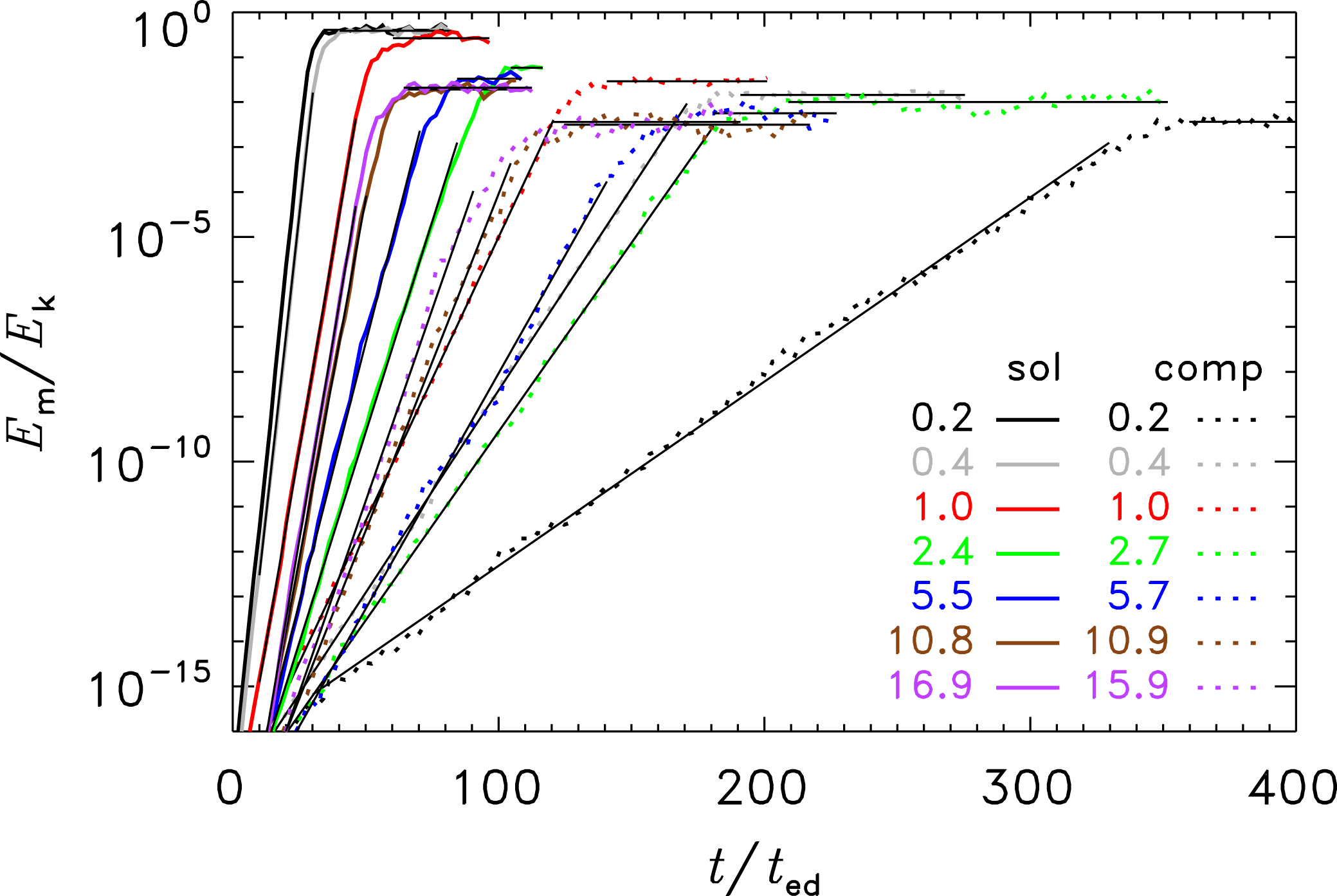
Figure 2. Magnetic-to-kinetic energy ratio (
![]() $E_{m}/E_{k}$
) as a function of the turbulent crossing time (
$E_{m}/E_{k}$
) as a function of the turbulent crossing time (
![]() $t/t_{ed}$
) for all runs with solenoidal (sol) and compressive (comp) driving. The time-averaged sonic Mach number (
$t/t_{ed}$
) for all runs with solenoidal (sol) and compressive (comp) driving. The time-averaged sonic Mach number (
![]() ${\mathcal{M}}$
) of each model is indicated in the legend (see figure 1 for the time evolution of
${\mathcal{M}}$
) of each model is indicated in the legend (see figure 1 for the time evolution of
![]() ${\mathcal{M}}$
). The thin solid lines show exponential fits in the regime of turbulent dynamo amplification, followed by constant fits in the saturation phase. The evolution of
${\mathcal{M}}$
). The thin solid lines show exponential fits in the regime of turbulent dynamo amplification, followed by constant fits in the saturation phase. The evolution of
![]() $E_{m}/E_{k}$
reveals extremely different efficiencies of the dynamo, depending on the Mach number and driving of the turbulence.
$E_{m}/E_{k}$
reveals extremely different efficiencies of the dynamo, depending on the Mach number and driving of the turbulence.
Figure 2 shows the ratio of magnetic-to-kinetic energy (
![]() $E_{m}/E_{k}$
) as a function of time. We immediately see that the magnetic energy grows exponentially over several orders of magnitude in any of the simulation models and finally reaches saturation at different levels (indicated by the fitted constant line towards late times when the curves saturate).
$E_{m}/E_{k}$
) as a function of time. We immediately see that the magnetic energy grows exponentially over several orders of magnitude in any of the simulation models and finally reaches saturation at different levels (indicated by the fitted constant line towards late times when the curves saturate).
Figure 3. Three-dimensional renderings of the gas density contrast on a logarithmic scale (
![]() $0.5\leqslant \unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}\leqslant 50$
) (from white to blue) and magnetic field lines (orange) for solenoidal driving at
$0.5\leqslant \unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}\leqslant 50$
) (from white to blue) and magnetic field lines (orange) for solenoidal driving at
![]() ${\mathcal{M}}=0.1$
(a) and
${\mathcal{M}}=0.1$
(a) and
![]() ${\mathcal{M}}=10$
(c), and compressive driving at
${\mathcal{M}}=10$
(c), and compressive driving at
![]() ${\mathcal{M}}=0.1$
(b) and
${\mathcal{M}}=0.1$
(b) and
![]() ${\mathcal{M}}=10$
(d). The stretch-twist-fold mechanism of the dynamo (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005) is evident in all models, but operates with different efficiency due to the varying compressibility, flow structure and formation of shocks in the supersonic plasmas. From Federrath et al. (Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
). An animation is available at https://www.mso.anu.edu.au/∼chfeder/pubs/dynamo_prl/dynamo_prl.html.
${\mathcal{M}}=10$
(d). The stretch-twist-fold mechanism of the dynamo (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005) is evident in all models, but operates with different efficiency due to the varying compressibility, flow structure and formation of shocks in the supersonic plasmas. From Federrath et al. (Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
). An animation is available at https://www.mso.anu.edu.au/∼chfeder/pubs/dynamo_prl/dynamo_prl.html.
2.3.2 Density and magnetic field structure
Figure 3 shows 3-D volume renderings of some of the extreme cases (solenoidal driving on the left and compressive driving on the right, each for
![]() ${\mathcal{M}}=0.1$
in a,b and
${\mathcal{M}}=0.1$
in a,b and
![]() ${\mathcal{M}}=10$
in c,d). We see that the supersonic simulation runs (c,d) are dominated by shocks. Compressive driving yields stronger density enhancements for similar Mach numbers compared to solenoidal driving (Nordlund & Padoan Reference Nordlund, Padoan, Franco and Carraminana1999; Federrath et al.
Reference Federrath, Klessen and Schmidt2008, Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Price, Federrath & Brunt Reference Price, Federrath and Brunt2011; Konstandin et al.
Reference Konstandin, Girichidis, Federrath and Klessen2012; Federrath Reference Federrath2013; Federrath & Klessen Reference Federrath and Klessen2013; Ginsburg, Federrath & Darling Reference Ginsburg, Federrath and Darling2013; Kainulainen, Federrath & Henning Reference Kainulainen, Federrath and Henning2013). The magnetic field occupies large volume fractions with relatively straight field lines in the compressively driven cases, while solenoidal driving produces more space-filling, tangled field configurations. This suggests that the turbulent dynamo operates more efficiently in the case of solenoidal driving, which is quantified and explained in the following.
${\mathcal{M}}=10$
in c,d). We see that the supersonic simulation runs (c,d) are dominated by shocks. Compressive driving yields stronger density enhancements for similar Mach numbers compared to solenoidal driving (Nordlund & Padoan Reference Nordlund, Padoan, Franco and Carraminana1999; Federrath et al.
Reference Federrath, Klessen and Schmidt2008, Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Price, Federrath & Brunt Reference Price, Federrath and Brunt2011; Konstandin et al.
Reference Konstandin, Girichidis, Federrath and Klessen2012; Federrath Reference Federrath2013; Federrath & Klessen Reference Federrath and Klessen2013; Ginsburg, Federrath & Darling Reference Ginsburg, Federrath and Darling2013; Kainulainen, Federrath & Henning Reference Kainulainen, Federrath and Henning2013). The magnetic field occupies large volume fractions with relatively straight field lines in the compressively driven cases, while solenoidal driving produces more space-filling, tangled field configurations. This suggests that the turbulent dynamo operates more efficiently in the case of solenoidal driving, which is quantified and explained in the following.
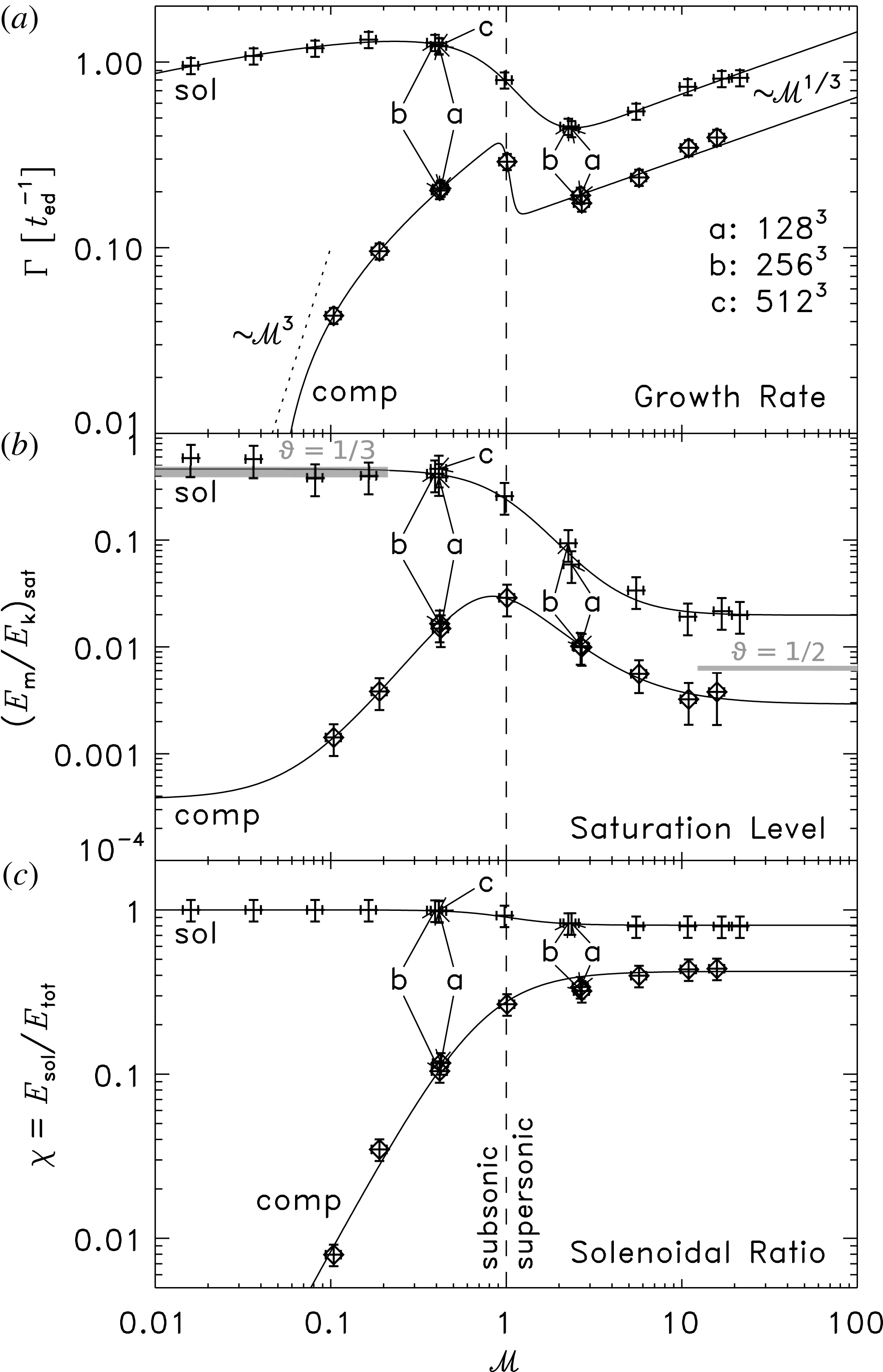
Figure 4. Growth rate (a), saturation level (b) and solenoidal ratio (c) as a function of Mach number, for all simulations with solenoidal (crosses) and compressive driving (diamonds). The thin solid lines show empirical fits with (2.9), the parameters of which are listed in table 1. The arrows point to four simulations (
![]() ${\mathcal{M}}\approx 0.4$
,
${\mathcal{M}}\approx 0.4$
,
![]() $2.5$
for solenoidal and compressive driving), which used ideal MHD on
$2.5$
for solenoidal and compressive driving), which used ideal MHD on
![]() $128^{3}$
grid cells (a), non-ideal MHD on
$128^{3}$
grid cells (a), non-ideal MHD on
![]() $256^{3}$
(b), and
$256^{3}$
(b), and
![]() $512^{3}$
grid cells (c), demonstrating convergence for the given magnetic Prandtl number,
$512^{3}$
grid cells (c), demonstrating convergence for the given magnetic Prandtl number,
![]() $Pm\approx 2$
, and kinematic Reynolds number,
$Pm\approx 2$
, and kinematic Reynolds number,
![]() $\mathit{Re}\approx 1500$
. The theoretical predictions for the saturation level from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are added as grey lines (middle panel) in the limit
$\mathit{Re}\approx 1500$
. The theoretical predictions for the saturation level from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are added as grey lines (middle panel) in the limit
![]() ${\mathcal{M}}\ll 1$
(Kolmogorov scaling exponent:
${\mathcal{M}}\ll 1$
(Kolmogorov scaling exponent:
![]() $\unicode[STIX]{x1D717}=1/3$
) and
$\unicode[STIX]{x1D717}=1/3$
) and
![]() ${\mathcal{M}}\gg 1$
(Burgers scaling exponent:
${\mathcal{M}}\gg 1$
(Burgers scaling exponent:
![]() $\unicode[STIX]{x1D717}=1/2$
).
$\unicode[STIX]{x1D717}=1/2$
).
2.3.3 Dynamo growth rate and saturation level
Figure 4(a,b) show the dynamo growth rate (
![]() $\unicode[STIX]{x1D6E4}$
) in the relation
$\unicode[STIX]{x1D6E4}$
) in the relation
![]() $E_{m}=E_{m0}\exp (\unicode[STIX]{x1D6E4}t)$
and the saturation level
$E_{m}=E_{m0}\exp (\unicode[STIX]{x1D6E4}t)$
and the saturation level
![]() $(E_{m}/E_{k})_{sat}$
as a function of Mach number for all simulation models. Both
$(E_{m}/E_{k})_{sat}$
as a function of Mach number for all simulation models. Both
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $(E_{m}/E_{k})_{sat}$
depend on
$(E_{m}/E_{k})_{sat}$
depend on
![]() ${\mathcal{M}}$
and on the driving of the turbulence. Solenoidal driving yields growth rates and saturation levels higher than for compressive driving. Both
${\mathcal{M}}$
and on the driving of the turbulence. Solenoidal driving yields growth rates and saturation levels higher than for compressive driving. Both
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $(E_{m}/E_{k})_{sat}$
change significantly at the transition from subsonic to supersonic turbulence. Within a turbulent medium, the transition from supersonic to subsonic turbulence occurs on the sonic scale (Vázquez-Semadeni, Ballesteros-Paredes & Klessen Reference Vázquez-Semadeni, Ballesteros-Paredes and Klessen2003; Federrath & Klessen Reference Federrath and Klessen2012; Hopkins Reference Hopkins2013; Federrath Reference Federrath2016). We conclude that the formation of shocks at
$(E_{m}/E_{k})_{sat}$
change significantly at the transition from subsonic to supersonic turbulence. Within a turbulent medium, the transition from supersonic to subsonic turbulence occurs on the sonic scale (Vázquez-Semadeni, Ballesteros-Paredes & Klessen Reference Vázquez-Semadeni, Ballesteros-Paredes and Klessen2003; Federrath & Klessen Reference Federrath and Klessen2012; Hopkins Reference Hopkins2013; Federrath Reference Federrath2016). We conclude that the formation of shocks at
![]() ${\mathcal{M}}\approx 1$
is responsible for destroying some of the coherent vortex motions necessary to drive the dynamo (Haugen et al.
Reference Haugen, Brandenburg and Mee2004b
). However, as
${\mathcal{M}}\approx 1$
is responsible for destroying some of the coherent vortex motions necessary to drive the dynamo (Haugen et al.
Reference Haugen, Brandenburg and Mee2004b
). However, as
![]() ${\mathcal{M}}$
is increased further, vorticity generation in oblique, colliding shocks (Sun & Takayama Reference Sun and Takayama2003; Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007) starts to dominate over the destruction of vorticity.
${\mathcal{M}}$
is increased further, vorticity generation in oblique, colliding shocks (Sun & Takayama Reference Sun and Takayama2003; Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007) starts to dominate over the destruction of vorticity.
The data points labelled with ‘a’, ‘b’ and ‘c’ in figure 4 show simulations with different numerical resolution (
![]() $128^{3}$
,
$128^{3}$
,
![]() $256^{3}$
and
$256^{3}$
and
![]() $512^{3}$
cells, respectively) and with different numerical solvers/schemes (‘a’: HLL3R with
$512^{3}$
cells, respectively) and with different numerical solvers/schemes (‘a’: HLL3R with
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D702}$
set to zero, i.e. ideal MHD; ‘b’ and ‘c’: HLLD with non-ideal MHD; cf. § 2.2). These convergence studies demonstrate that our results do not depend on the choice of numerical solver and, in particular, do not depend on the choice of dissipation mechanism (see also Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). The reason for this is that the physical dissipation was chosen to be similar to the numerical one in the low-resolution simulations, while in the high-resolution simulations, the physical dissipation dominates the numerical dissipation. This is why our simulations are converged and the results do not depend on the choice of numerical solver.
$\unicode[STIX]{x1D702}$
set to zero, i.e. ideal MHD; ‘b’ and ‘c’: HLLD with non-ideal MHD; cf. § 2.2). These convergence studies demonstrate that our results do not depend on the choice of numerical solver and, in particular, do not depend on the choice of dissipation mechanism (see also Benzi et al.
Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993). The reason for this is that the physical dissipation was chosen to be similar to the numerical one in the low-resolution simulations, while in the high-resolution simulations, the physical dissipation dominates the numerical dissipation. This is why our simulations are converged and the results do not depend on the choice of numerical solver.
The very small growth rates in the subsonic, compressively driven models are due to the fact that hardly any vorticity is generated. In order to quantify this, we show the solenoidal ratio, i.e. the specific kinetic energy in solenoidal modes of the turbulent velocity field divided by the total specific kinetic energy,
![]() $\unicode[STIX]{x1D712}=E_{sol}/E_{tot}$
in the bottom panel of figure 4. We see that the solenoidal ratio drops sharply towards lower Mach numbers in the case of compressive driving. In the absence of the baroclinic term,
$\unicode[STIX]{x1D712}=E_{sol}/E_{tot}$
in the bottom panel of figure 4. We see that the solenoidal ratio drops sharply towards lower Mach numbers in the case of compressive driving. In the absence of the baroclinic term,
![]() $(1/\unicode[STIX]{x1D70C}^{2})\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D735}p_{th}$
, the only way to generate vorticity,
$(1/\unicode[STIX]{x1D70C}^{2})\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D735}p_{th}$
, the only way to generate vorticity,
![]() $\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
, with compressive (curl-free) driving is via viscous interactions in the vorticity equation (Mee & Brandenburg Reference Mee and Brandenburg2006),
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
, with compressive (curl-free) driving is via viscous interactions in the vorticity equation (Mee & Brandenburg Reference Mee and Brandenburg2006),
While the second term on the right-hand side is diffusive and dampens
![]() $\unicode[STIX]{x1D74E}$
, the last term can actually generate vorticity through viscous interactions in the presence of logarithmic density gradients. Thus, even in the absence of initial vorticity, small seeds of
$\unicode[STIX]{x1D74E}$
, the last term can actually generate vorticity through viscous interactions in the presence of logarithmic density gradients. Thus, even in the absence of initial vorticity, small seeds of
![]() $\unicode[STIX]{x1D74E}$
can be generated. Those are then exponentially amplified by the nonlinear term,
$\unicode[STIX]{x1D74E}$
can be generated. Those are then exponentially amplified by the nonlinear term,
![]() $\unicode[STIX]{x1D735}\times \left(\boldsymbol{u}\times \unicode[STIX]{x1D74E}\right)$
, if the Reynolds numbers are sufficiently large (Frisch Reference Frisch1995)Footnote
1
. For very low Mach numbers, however, density gradients start to vanish, thus explaining the steep drop of the dynamo growth rate for compressively driven turbulence with low Mach numbers.
$\unicode[STIX]{x1D735}\times \left(\boldsymbol{u}\times \unicode[STIX]{x1D74E}\right)$
, if the Reynolds numbers are sufficiently large (Frisch Reference Frisch1995)Footnote
1
. For very low Mach numbers, however, density gradients start to vanish, thus explaining the steep drop of the dynamo growth rate for compressively driven turbulence with low Mach numbers.
Analytic estimates by Moss & Shukurov (Reference Moss and Shukurov1996) suggest that the dynamo growth rate
![]() $\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{3}$
in compressively driven, acoustic turbulence, shown as the dotted line in figure 4(a) (we note that we defined
$\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{3}$
in compressively driven, acoustic turbulence, shown as the dotted line in figure 4(a) (we note that we defined
![]() $t_{ed}=L/(2{\mathcal{M}}c_{s})$
, while Moss & Shukurov (Reference Moss and Shukurov1996) defined
$t_{ed}=L/(2{\mathcal{M}}c_{s})$
, while Moss & Shukurov (Reference Moss and Shukurov1996) defined
![]() $t_{ed}=L/(2c_{s})$
, which differs by a factor of
$t_{ed}=L/(2c_{s})$
, which differs by a factor of
![]() ${\mathcal{M}}$
from our definition). Our simulations are consistent with this, though simulations at even lower Mach number for compressive driving are required to confirm the
${\mathcal{M}}$
from our definition). Our simulations are consistent with this, though simulations at even lower Mach number for compressive driving are required to confirm the
![]() $\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{3}$
scaling.
$\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{3}$
scaling.
The solid lines in figure 4 show fits with the empirical function,
The fit parameters are given in table 1. We caution that these fits do not necessarily reflect the true asymptotic behaviour of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $(E_{m}/E_{k})_{sat}$
, but they provide a reasonably good fit for the range of Mach numbers tested in our simulations.
$(E_{m}/E_{k})_{sat}$
, but they provide a reasonably good fit for the range of Mach numbers tested in our simulations.
The subsonic, solenoidally driven models show very high saturation levels,
![]() $(E_{m}/E_{k})_{sat}\approx 40$
–60 %, in excellent agreement with the theoretical predictions from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) for Kolmogorov (Reference Kolmogorov1941) turbulence (velocity scaling exponent
$(E_{m}/E_{k})_{sat}\approx 40$
–60 %, in excellent agreement with the theoretical predictions from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) for Kolmogorov (Reference Kolmogorov1941) turbulence (velocity scaling exponent
![]() $\unicode[STIX]{x1D717}=1/3$
). On the other hand, for the highly compressible, supersonic limit, Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) predict
$\unicode[STIX]{x1D717}=1/3$
). On the other hand, for the highly compressible, supersonic limit, Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) predict
![]() ${\sim}100$
times lower saturation levels, of the order of
${\sim}100$
times lower saturation levels, of the order of
![]() $0.6\,\%$
, which is qualitatively consistent with our MHD simulations. The prediction by Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) for
$0.6\,\%$
, which is qualitatively consistent with our MHD simulations. The prediction by Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) for
![]() ${\mathcal{M}}\gg 1$
is based on the scaling exponent of supersonic Burgers (Reference Burgers1948) turbulence,
${\mathcal{M}}\gg 1$
is based on the scaling exponent of supersonic Burgers (Reference Burgers1948) turbulence,
![]() $\unicode[STIX]{x1D717}=1/2$
, which is indeed measured in numerical simulations (Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Federrath Reference Federrath2013).
$\unicode[STIX]{x1D717}=1/2$
, which is indeed measured in numerical simulations (Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Federrath Reference Federrath2013).
The high saturation levels in the case of subsonic, solenoidally driven turbulence cause a strong back reaction of the magnetic field, explaining the Mach number drop in the saturation regime that we saw in figure 1 for these models. This is consistent with the simulations in Haugen, Brandenburg & Dobler (Reference Haugen, Brandenburg and Dobler2003, Reference Haugen, Brandenburg and Dobler2004a
). For the growth rate, we fix
![]() $p_{6}$
such that
$p_{6}$
such that
![]() $\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{1/3}$
for
$\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{1/3}$
for
![]() ${\mathcal{M}}\gg 1$
, in good agreement with our models up to
${\mathcal{M}}\gg 1$
, in good agreement with our models up to
![]() ${\mathcal{M}}\approx 20$
. However, simulations with even higher
${\mathcal{M}}\approx 20$
. However, simulations with even higher
![]() ${\mathcal{M}}$
are required to see if
${\mathcal{M}}$
are required to see if
![]() $\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{1/3}$
holds in this limit. We find that
$\unicode[STIX]{x1D6E4}\propto {\mathcal{M}}^{1/3}$
holds in this limit. We find that
![]() $\unicode[STIX]{x1D6E4}$
depends much less on
$\unicode[STIX]{x1D6E4}$
depends much less on
![]() ${\mathcal{M}}$
in the case of solenoidal driving. Nevertheless, a drop of the growth rate at
${\mathcal{M}}$
in the case of solenoidal driving. Nevertheless, a drop of the growth rate at
![]() ${\mathcal{M}}\approx 1$
is present in both driving cases.
${\mathcal{M}}\approx 1$
is present in both driving cases.
Dynamo theories based on the phenomenological model of incompressible, purely solenoidal turbulence by Kolmogorov (Reference Kolmogorov1941) predict no dependence of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() ${\mathcal{M}}$
. For instance, Subramanian (Reference Subramanian1997) derived
${\mathcal{M}}$
. For instance, Subramanian (Reference Subramanian1997) derived
![]() $\unicode[STIX]{x1D6E4}=(15/24)\mathit{Re}^{1/2}t_{ed}^{-1}$
based on the Kolmogorov–Fokker–Planck equation, in the limit of large magnetic Prandtl number,
$\unicode[STIX]{x1D6E4}=(15/24)\mathit{Re}^{1/2}t_{ed}^{-1}$
based on the Kolmogorov–Fokker–Planck equation, in the limit of large magnetic Prandtl number,
![]() $Pm=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}=Rm/Re\gg 1$
with the kinetic and magnetic Reynolds numbers
$Pm=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}=Rm/Re\gg 1$
with the kinetic and magnetic Reynolds numbers
![]() $\mathit{Re}=Lu_{turb}/(2\unicode[STIX]{x1D708})$
and
$\mathit{Re}=Lu_{turb}/(2\unicode[STIX]{x1D708})$
and
![]() $Rm=Lu_{turb}/(2\unicode[STIX]{x1D702})$
. For
$Rm=Lu_{turb}/(2\unicode[STIX]{x1D702})$
. For
![]() $Pm\approx 2$
(which is typically the result of numerical dissipation in the ideal MHD approximation; see Lesaffre & Balbus Reference Lesaffre and Balbus2007), and
$Pm\approx 2$
(which is typically the result of numerical dissipation in the ideal MHD approximation; see Lesaffre & Balbus Reference Lesaffre and Balbus2007), and
![]() $\mathit{Re}\approx 1500$
, corresponding to our simulations, we find slightly smaller growth rates than predicted in Subramanian (Reference Subramanian1997), but in agreement with analytic considerations (Boldyrev & Cattaneo Reference Boldyrev and Cattaneo2004), and with numerical simulations of incompressible turbulence for
$\mathit{Re}\approx 1500$
, corresponding to our simulations, we find slightly smaller growth rates than predicted in Subramanian (Reference Subramanian1997), but in agreement with analytic considerations (Boldyrev & Cattaneo Reference Boldyrev and Cattaneo2004), and with numerical simulations of incompressible turbulence for
![]() $Pm\approx 1$
(Schekochihin et al.
Reference Schekochihin, Iskakov, Cowley, McWilliams, Proctor and Yousef2007; Cho et al.
Reference Cho, Vishniac, Beresnyak, Lazarian and Ryu2009). Thus, an extension of the dynamo theory to small
$Pm\approx 1$
(Schekochihin et al.
Reference Schekochihin, Iskakov, Cowley, McWilliams, Proctor and Yousef2007; Cho et al.
Reference Cho, Vishniac, Beresnyak, Lazarian and Ryu2009). Thus, an extension of the dynamo theory to small
![]() $Pm$
is needed and will be presented in § 3 below. Moreover, extending the theory from Kolmogorov to Burgers, shock-dominated turbulence is a necessary next step in order to develop a more generalised theory of turbulent dynamos, potentially with predictive power for the supersonic, highly compressible regime.
$Pm$
is needed and will be presented in § 3 below. Moreover, extending the theory from Kolmogorov to Burgers, shock-dominated turbulence is a necessary next step in order to develop a more generalised theory of turbulent dynamos, potentially with predictive power for the supersonic, highly compressible regime.
In summary, we find that the growth rate and saturation level of the turbulent dynamo strongly depend on the Mach number and the driving of the turbulence. We conclude that the compressibility of the plasma plays a crucial role for the amplification of turbulent magnetic fields.
3 Dependence of the dynamo on the magnetic Prandtl number
Previous studies of incompressible turbulence have demonstrated that the turbulent dynamo depends on the magnetic Prandtl number,
![]() $Pm=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}=Rm/\mathit{Re}$
, defined as the ratio of kinematic viscosity
$Pm=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D702}=Rm/\mathit{Re}$
, defined as the ratio of kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
to magnetic diffusivity
$\unicode[STIX]{x1D708}$
to magnetic diffusivity
![]() $\unicode[STIX]{x1D702}$
(Schekochihin et al.
Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004). The magnetic Prandtl number also plays a role for the magnetorotational instability and the transport of angular momentum in accretion disks (Fromang Reference Fromang2010; Fromang et al.
Reference Fromang, Papaloizou, Lesur, Heinemann, Montmerle, Ehrenreich and Lagrange2010).
$\unicode[STIX]{x1D702}$
(Schekochihin et al.
Reference Schekochihin, Cowley, Taylor, Maron and McWilliams2004). The magnetic Prandtl number also plays a role for the magnetorotational instability and the transport of angular momentum in accretion disks (Fromang Reference Fromang2010; Fromang et al.
Reference Fromang, Papaloizou, Lesur, Heinemann, Montmerle, Ehrenreich and Lagrange2010).
Here we extend this study of
![]() $Pm$
into the compressible, supersonic regime of turbulence. Some of the results discussed in this section are published in Federrath et al. (Reference Federrath, Schober, Bovino and Schleicher2014a
).
$Pm$
into the compressible, supersonic regime of turbulence. Some of the results discussed in this section are published in Federrath et al. (Reference Federrath, Schober, Bovino and Schleicher2014a
).
On large cosmological scales and in the interstellar medium, we typically have
![]() $Pm\gg 1$
(for details on how to estimate the viscosity and magnetic diffusivity, see Wardle & Ng Reference Wardle and Ng1999; Pinto & Galli Reference Pinto and Galli2008; Schober et al.
Reference Schober, Schleicher, Federrath, Glover, Klessen and Banerjee2012b
; Krumholz Reference Krumholz2014, for example, in molecular clouds, we have
$Pm\gg 1$
(for details on how to estimate the viscosity and magnetic diffusivity, see Wardle & Ng Reference Wardle and Ng1999; Pinto & Galli Reference Pinto and Galli2008; Schober et al.
Reference Schober, Schleicher, Federrath, Glover, Klessen and Banerjee2012b
; Krumholz Reference Krumholz2014, for example, in molecular clouds, we have
![]() $Re\approx 10^{7}$
and
$Re\approx 10^{7}$
and
![]() $Rm\approx 10^{17}$
, hence
$Rm\approx 10^{17}$
, hence
![]() $Pm\approx 10^{10}$
), while for the interior of stars and planets, the case with
$Pm\approx 10^{10}$
), while for the interior of stars and planets, the case with
![]() $Pm\ll 1$
is more relevant (Schekochihin et al.
Reference Schekochihin, Iskakov, Cowley, McWilliams, Proctor and Yousef2007). However, numerical simulations are typically restricted to
$Pm\ll 1$
is more relevant (Schekochihin et al.
Reference Schekochihin, Iskakov, Cowley, McWilliams, Proctor and Yousef2007). However, numerical simulations are typically restricted to
![]() $Pm\approx 1$
, because of limited scale separation that can be achieved with currently accessible numerical resolutions. Simulations by Iskakov et al. (Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007) have demonstrated that the turbulent dynamo operates for
$Pm\approx 1$
, because of limited scale separation that can be achieved with currently accessible numerical resolutions. Simulations by Iskakov et al. (Reference Iskakov, Schekochihin, Cowley, McWilliams and Proctor2007) have demonstrated that the turbulent dynamo operates for
![]() $Pm\lesssim 1$
in incompressible gases, even though an asymptotic scaling relation could not be confirmed. While the bulk of previous work was dedicated to exploring the turbulent dynamo for incompressible plasmas (Brandenburg, Sokoloff & Subramanian Reference Brandenburg, Sokoloff and Subramanian2012), most astrophysical systems show signs of high compressibility. This is especially true for the early Universe when the first stars and galaxies formed (Latif, Schleicher & Schmidt Reference Latif, Schleicher and Schmidt2014), in the interstellar medium of present-day galaxies (Larson Reference Larson1981), as well as in the intergalactic medium (Vazza et al.
Reference Vazza, Brunetti, Kritsuk, Wagner, Gheller and Norman2009; Iapichino, Viel & Borgani Reference Iapichino, Viel and Borgani2013; Miniati & Beresnyak Reference Miniati and Beresnyak2015). As in § 2, the compressibility of the plasma is characterised in terms of the sonic Mach number
$Pm\lesssim 1$
in incompressible gases, even though an asymptotic scaling relation could not be confirmed. While the bulk of previous work was dedicated to exploring the turbulent dynamo for incompressible plasmas (Brandenburg, Sokoloff & Subramanian Reference Brandenburg, Sokoloff and Subramanian2012), most astrophysical systems show signs of high compressibility. This is especially true for the early Universe when the first stars and galaxies formed (Latif, Schleicher & Schmidt Reference Latif, Schleicher and Schmidt2014), in the interstellar medium of present-day galaxies (Larson Reference Larson1981), as well as in the intergalactic medium (Vazza et al.
Reference Vazza, Brunetti, Kritsuk, Wagner, Gheller and Norman2009; Iapichino, Viel & Borgani Reference Iapichino, Viel and Borgani2013; Miniati & Beresnyak Reference Miniati and Beresnyak2015). As in § 2, the compressibility of the plasma is characterised in terms of the sonic Mach number
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Based on the Kazantsev model (Kazantsev Reference Kazantsev1968; Kazantsev, Ruzmaikin & Sokolov Reference Kazantsev, Ruzmaikin and Sokolov1985) (see also recent work by Xu & Lazarian 2016), Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) derived an analytical dynamo solution for the limiting cases
![]() $Pm\rightarrow \infty$
and
$Pm\rightarrow \infty$
and
![]() $Pm\rightarrow 0$
, considering different scaling relations of the turbulence. Bovino, Schleicher & Schober (Reference Bovino, Schleicher and Schober2013) later computed numerical solutions of the Kazantsev equation for intermediate values of
$Pm\rightarrow 0$
, considering different scaling relations of the turbulence. Bovino, Schleicher & Schober (Reference Bovino, Schleicher and Schober2013) later computed numerical solutions of the Kazantsev equation for intermediate values of
![]() $Pm$
. These theoretical studies suggested that the turbulent dynamo operates for a range of
$Pm$
. These theoretical studies suggested that the turbulent dynamo operates for a range of
![]() $Pm$
, as long as the magnetic Reynolds number is sufficiently high. A central restriction of the Kazantsev model is the assumption of an incompressible velocity field, for which a separation into solenoidal and compressible parts is not necessary. But the distinction between solenoidal and compressible modes is essential for highly compressible, supersonic turbulence (see § 2). Moreover, the Kazantsev framework assumes that the turbulence is
$Pm$
, as long as the magnetic Reynolds number is sufficiently high. A central restriction of the Kazantsev model is the assumption of an incompressible velocity field, for which a separation into solenoidal and compressible parts is not necessary. But the distinction between solenoidal and compressible modes is essential for highly compressible, supersonic turbulence (see § 2). Moreover, the Kazantsev framework assumes that the turbulence is
![]() $\unicode[STIX]{x1D6FF}$
-correlated in time, but the resulting uncertainties introduced by this assumption are only a few per cent (Schekochihin & Kulsrud Reference Schekochihin and Kulsrud2001; Kleeorin, Rogachevskii & Sokoloff Reference Kleeorin, Rogachevskii and Sokoloff2002; Bhat & Subramanian Reference Bhat and Subramanian2014). However, the assumption of incompressibility may introduce significantly higher uncertainties in the analytic and semi-analytic estimates based on the Kazantsev model. Ultimately one needs full 3-D simulations to determine the dependence of the dynamo growth rates and saturation levels on
$\unicode[STIX]{x1D6FF}$
-correlated in time, but the resulting uncertainties introduced by this assumption are only a few per cent (Schekochihin & Kulsrud Reference Schekochihin and Kulsrud2001; Kleeorin, Rogachevskii & Sokoloff Reference Kleeorin, Rogachevskii and Sokoloff2002; Bhat & Subramanian Reference Bhat and Subramanian2014). However, the assumption of incompressibility may introduce significantly higher uncertainties in the analytic and semi-analytic estimates based on the Kazantsev model. Ultimately one needs full 3-D simulations to determine the dependence of the dynamo growth rates and saturation levels on
![]() $Pm$
.
$Pm$
.
Here we present a systematic study of the turbulent dynamo and its dependence on the magnetic Prandtl number in the highly compressible regime. For this purpose, we consider supersonic turbulence with
![]() ${\mathcal{M}}=4$
–
${\mathcal{M}}=4$
–
![]() $11$
, and magnetic Prandtl numbers between
$11$
, and magnetic Prandtl numbers between
![]() $Pm=0.1$
and
$Pm=0.1$
and
![]() $10$
. The simulation results are compared with analytic and semi-analytic predictions based on the Kazantsev model.
$10$
. The simulation results are compared with analytic and semi-analytic predictions based on the Kazantsev model.
3.1 Numerical simulations
The simulations follow the same basic approach as explained in detail in § 2.2. We run most of the simulations until saturation of the magnetic field is reached. We determine the growth rate by fitting an exponential function to the time evolution of the magnetic energy. The saturation level is determined by measuring the magnetic-to-kinetic energy ratio
![]() $(E_{m}/E_{k})_{sat}$
in the saturated phase. We note that the turbulent dynamo has also been studied with ‘shell models’ (Frick, Stepanov & Sokoloff Reference Frick, Stepanov and Sokoloff2006, and references therein). Shell models can also provide theoretical predictions for the magnetic energy growth in the exponential and saturated regimes of the dynamo and they are complementary to the 3-D numerical simulations presented here.
$(E_{m}/E_{k})_{sat}$
in the saturated phase. We note that the turbulent dynamo has also been studied with ‘shell models’ (Frick, Stepanov & Sokoloff Reference Frick, Stepanov and Sokoloff2006, and references therein). Shell models can also provide theoretical predictions for the magnetic energy growth in the exponential and saturated regimes of the dynamo and they are complementary to the 3-D numerical simulations presented here.
Table 2. Turbulent dynamo simulations with different magnetic Prandtl number (
![]() $Pm$
).
$Pm$
).
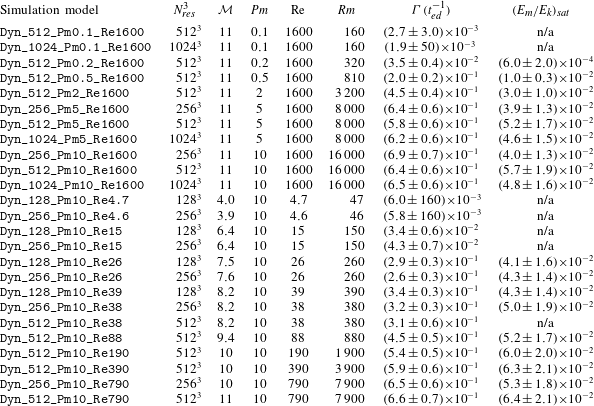
Here we study the dependence of the turbulent dynamo on
![]() $Pm$
, which is accomplished by varying the physical viscosity and magnetic diffusivity. Table 2 provides a complete list of all simulations and key parameters. The MHD equations (2.1)–(2.5) are solved with the positive–definite second-order accurate HLL3R Riemann scheme (Waagan et al.
Reference Waagan, Federrath and Klingenberg2011). As a numerical convergence test, we run simulations with
$Pm$
, which is accomplished by varying the physical viscosity and magnetic diffusivity. Table 2 provides a complete list of all simulations and key parameters. The MHD equations (2.1)–(2.5) are solved with the positive–definite second-order accurate HLL3R Riemann scheme (Waagan et al.
Reference Waagan, Federrath and Klingenberg2011). As a numerical convergence test, we run simulations with
![]() $N_{res}^{3}=128^{3}$
–
$N_{res}^{3}=128^{3}$
–
![]() $1024^{3}$
grid points.
$1024^{3}$
grid points.
3.2 Dynamo theory
Most theoretical models of the turbulent dynamo are based on the Kazantsev framework (Kazantsev Reference Kazantsev1968; Rogachevskii & Kleeorin Reference Rogachevskii and Kleeorin1997; Subramanian Reference Subramanian1997; Brandenburg & Subramanian Reference Brandenburg and Subramanian2005), The Kazantsev equation assumes zero helicity,
![]() $\unicode[STIX]{x1D6FF}$
-correlation in time and does not take into account the mixture of solenoidal-to-compressible modes in the turbulent velocity field. These limitations are related to the fact that the Kazantsev equation was historically only applied to incompressible turbulence. Here we present an extension of the Kazantsev model to compressible, supersonic regime of turbulence (the details of which are published in Schober et al.
Reference Schober, Schleicher, Bovino and Klessen2012a
,Reference Schober, Schleicher, Federrath, Klessen and Banerjee
c
; Bovino et al.
Reference Bovino, Schleicher and Schober2013; Schleicher et al.
Reference Schleicher, Schober, Federrath, Bovino and Schmidt2013; Schober et al.
Reference Schober, Schleicher, Federrath, Bovino and Klessen2015).
$\unicode[STIX]{x1D6FF}$
-correlation in time and does not take into account the mixture of solenoidal-to-compressible modes in the turbulent velocity field. These limitations are related to the fact that the Kazantsev equation was historically only applied to incompressible turbulence. Here we present an extension of the Kazantsev model to compressible, supersonic regime of turbulence (the details of which are published in Schober et al.
Reference Schober, Schleicher, Bovino and Klessen2012a
,Reference Schober, Schleicher, Federrath, Klessen and Banerjee
c
; Bovino et al.
Reference Bovino, Schleicher and Schober2013; Schleicher et al.
Reference Schleicher, Schober, Federrath, Bovino and Schmidt2013; Schober et al.
Reference Schober, Schleicher, Federrath, Bovino and Klessen2015).
The form of the Kazantsev equation is similar to the Schrödinger equation. This allows us to solve the equation both numerically and analytically with standard methods from quantum mechanics such as the Wentzel–Kramers–Brillouin (WKB) approximation. In order find a solution, we have to assume a scaling of the turbulent velocity fluctuations
![]() $u_{turb}(\ell )$
in the inertial range (
$u_{turb}(\ell )$
in the inertial range (
![]() $\ell _{\unicode[STIX]{x1D708}}<\ell <L$
),
$\ell _{\unicode[STIX]{x1D708}}<\ell <L$
),
where
![]() $\ell _{\unicode[STIX]{x1D708}}$
and
$\ell _{\unicode[STIX]{x1D708}}$
and
![]() $L$
are the viscous and integral scales, respectively. The exponent
$L$
are the viscous and integral scales, respectively. The exponent
![]() $\unicode[STIX]{x1D717}$
varies from
$\unicode[STIX]{x1D717}$
varies from
![]() $1/3$
for incompressible, non-intermittent (Kolmogorov Reference Kolmogorov1941) turbulence up to
$1/3$
for incompressible, non-intermittent (Kolmogorov Reference Kolmogorov1941) turbulence up to
![]() $1/2$
for supersonic, shock-dominated turbulence (Burgers Reference Burgers1948). Based on numerical simulations of mildly supersonic turbulence with Mach numbers
$1/2$
for supersonic, shock-dominated turbulence (Burgers Reference Burgers1948). Based on numerical simulations of mildly supersonic turbulence with Mach numbers
![]() ${\mathcal{M}}\approx 2$
–
${\mathcal{M}}\approx 2$
–
![]() $7$
, scaling exponents
$7$
, scaling exponents
![]() $\unicode[STIX]{x1D717}\approx 0.37$
–
$\unicode[STIX]{x1D717}\approx 0.37$
–
![]() $0.47$
were found in numerical simulations (Boldyrev, Nordlund & Padoan Reference Boldyrev, Nordlund and Padoan2002; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Kowal & Lazarian Reference Kowal and Lazarian2010). Highly supersonic turbulence with
$0.47$
were found in numerical simulations (Boldyrev, Nordlund & Padoan Reference Boldyrev, Nordlund and Padoan2002; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Kowal & Lazarian Reference Kowal and Lazarian2010). Highly supersonic turbulence with
![]() ${\mathcal{M}}>15$
asymptotically approaches the Burgers limit,
${\mathcal{M}}>15$
asymptotically approaches the Burgers limit,
![]() $\unicode[STIX]{x1D717}=0.5$
(Federrath Reference Federrath2013). Observations of interstellar clouds suggest similar velocity scaling exponents with
$\unicode[STIX]{x1D717}=0.5$
(Federrath Reference Federrath2013). Observations of interstellar clouds suggest similar velocity scaling exponents with
![]() $\unicode[STIX]{x1D717}\approx 0.38$
–
$\unicode[STIX]{x1D717}\approx 0.38$
–
![]() $0.5$
(Larson Reference Larson1981; Solomon et al.
Reference Solomon, Rivolo, Barrett and Yahil1987; Ossenkopf & Mac Low Reference Ossenkopf and Mac Low2002; Heyer & Brunt Reference Heyer and Brunt2004; Roman-Duval et al.
Reference Roman-Duval, Federrath, Brunt, Heyer, Jackson and Klessen2011). Given this range of turbulence scaling exponents from numerical simulations and observations, we here compute theoretical estimates of the dynamo growth rate for
$0.5$
(Larson Reference Larson1981; Solomon et al.
Reference Solomon, Rivolo, Barrett and Yahil1987; Ossenkopf & Mac Low Reference Ossenkopf and Mac Low2002; Heyer & Brunt Reference Heyer and Brunt2004; Roman-Duval et al.
Reference Roman-Duval, Federrath, Brunt, Heyer, Jackson and Klessen2011). Given this range of turbulence scaling exponents from numerical simulations and observations, we here compute theoretical estimates of the dynamo growth rate for
![]() $\unicode[STIX]{x1D717}=0.35$
,
$\unicode[STIX]{x1D717}=0.35$
,
![]() $0.40$
and
$0.40$
and
![]() $0.45$
.
$0.45$
.
3.3 Results and discussion
3.3.1 Magnetic field structure in low-
 $Pm$
and high-
$Pm$
and high-
 $Pm$
supersonic plasmas
$Pm$
supersonic plasmas
Figure 5 provides a visual comparison of the differences in magnetic energy between low-
![]() $Pm$
and high-
$Pm$
and high-
![]() $Pm$
supersonic plasmas. Magnetic dissipation is stronger in low-
$Pm$
supersonic plasmas. Magnetic dissipation is stronger in low-
![]() $Pm$
compared to high-
$Pm$
compared to high-
![]() $Pm$
plasmas (for
$Pm$
plasmas (for
![]() $Re=\text{const.}$
). Here we find that the dynamo operates in both cases, but with extremely different efficiency. This is the first time that dynamo action was confirmed in
$Re=\text{const.}$
). Here we find that the dynamo operates in both cases, but with extremely different efficiency. This is the first time that dynamo action was confirmed in
![]() $Pm<1$
, highly compressible, supersonic plasmas (Federrath et al.
Reference Federrath, Schober, Bovino and Schleicher2014a
).
$Pm<1$
, highly compressible, supersonic plasmas (Federrath et al.
Reference Federrath, Schober, Bovino and Schleicher2014a
).

Figure 5. Magnetic energy slices through the mid-plane of our dynamo simulations with grid resolutions of
![]() $1024^{3}$
points. The magnetic field grows more slowly for low magnetic Prandtl number
$1024^{3}$
points. The magnetic field grows more slowly for low magnetic Prandtl number
![]() $Pm=0.1$
(left-hand panel) compared to
$Pm=0.1$
(left-hand panel) compared to
![]() $Pm=10$
(right-hand panel). However, dynamo action occurs in both cases, and for the first time shown in highly compressible, supersonic plasmas (Federrath et al.
Reference Federrath, Schober, Bovino and Schleicher2014a
). An animation is available at http://www.mso.anu.edu.au/∼chfeder/pubs/dynamo_pm/dynamo_pm.html.
$Pm=10$
(right-hand panel). However, dynamo action occurs in both cases, and for the first time shown in highly compressible, supersonic plasmas (Federrath et al.
Reference Federrath, Schober, Bovino and Schleicher2014a
). An animation is available at http://www.mso.anu.edu.au/∼chfeder/pubs/dynamo_pm/dynamo_pm.html.
3.3.2 Growth rate and saturation level as a function of
 $Pm$
and
$Pm$
and
 $Re$
$Re$
In order to compare the analytical and numerical solutions of the Kazantsev equation from § 3.2 with the MHD simulations, we now determine the dynamo growth rate as a function of
![]() $Pm$
for fixed
$Pm$
for fixed
![]() $Re=1600$
and as a function of
$Re=1600$
and as a function of
![]() $Re$
for fixed
$Re$
for fixed
![]() $Pm=10$
. Depending on
$Pm=10$
. Depending on
![]() $Pm$
and
$Pm$
and
![]() $Re$
we find exponential magnetic energy growth over more than six orders of magnitude for simulations in which the dynamo operates. We determine both the exponential growth rate
$Re$
we find exponential magnetic energy growth over more than six orders of magnitude for simulations in which the dynamo operates. We determine both the exponential growth rate
![]() $\unicode[STIX]{x1D6E4}$
and the saturation level
$\unicode[STIX]{x1D6E4}$
and the saturation level
![]() $(E_{m}/E_{k})_{sat}$
. The measurements are listed in table 2 and shown in figure 6.
$(E_{m}/E_{k})_{sat}$
. The measurements are listed in table 2 and shown in figure 6.
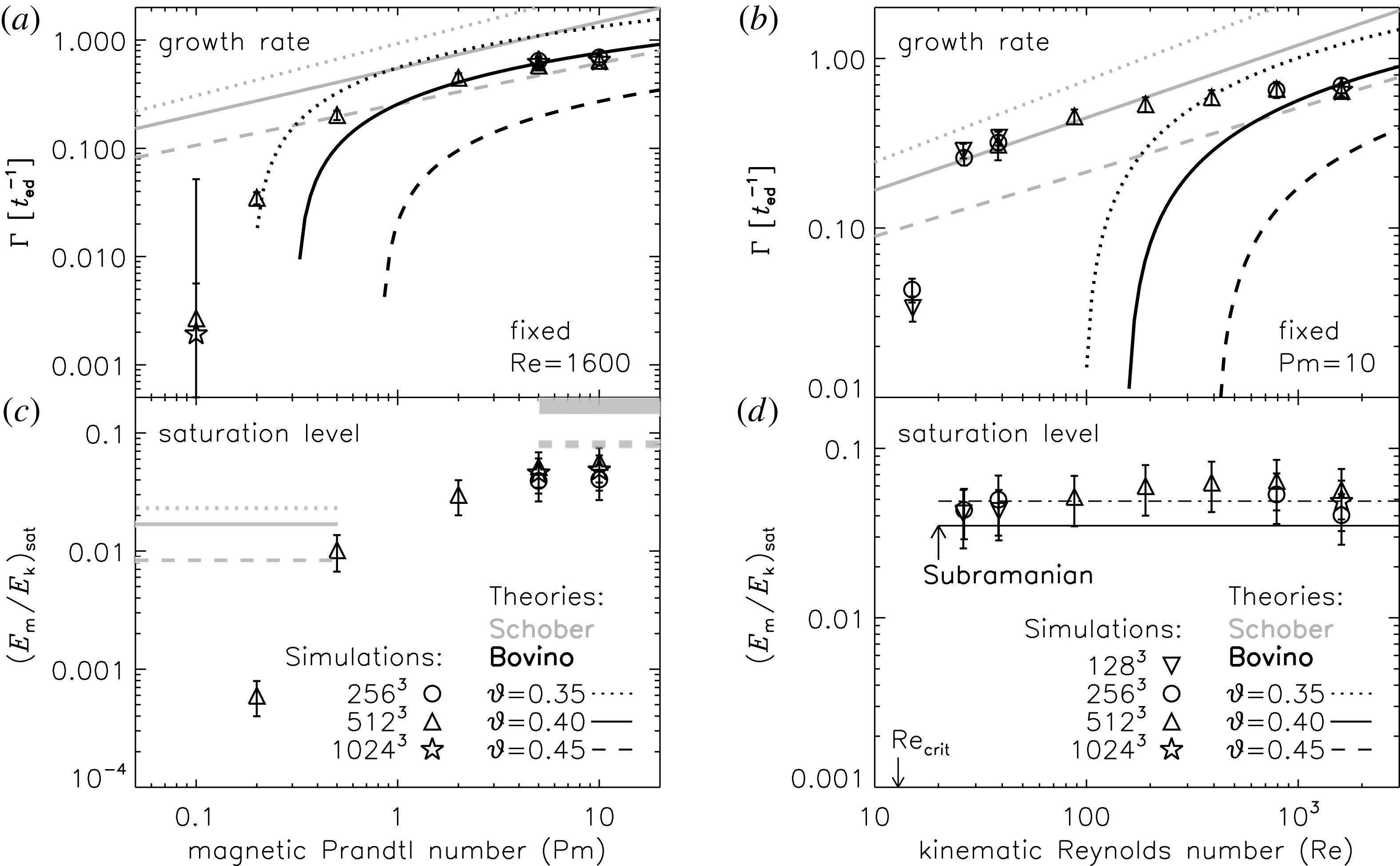
Figure 6. (a,c) Dynamo growth rate
![]() $\unicode[STIX]{x1D6E4}$
(a) and saturation level
$\unicode[STIX]{x1D6E4}$
(a) and saturation level
![]() $(E_{m}/E_{k})_{sat}$
(c) as a function of
$(E_{m}/E_{k})_{sat}$
(c) as a function of
![]() $Pm$
for fixed
$Pm$
for fixed
![]() $Re=1600$
. Resolution studies with
$Re=1600$
. Resolution studies with
![]() $256^{3}$
,
$256^{3}$
,
![]() $512^{3}$
and
$512^{3}$
and
![]() $1024^{3}$
grid cells demonstrate convergence, tested for the extreme cases
$1024^{3}$
grid cells demonstrate convergence, tested for the extreme cases
![]() $Pm=0.1$
and
$Pm=0.1$
and
![]() $10$
. Theoretical predictions for
$10$
. Theoretical predictions for
![]() $\unicode[STIX]{x1D6E4}$
by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) and Bovino et al. (Reference Bovino, Schleicher and Schober2013) and for
$\unicode[STIX]{x1D6E4}$
by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) and Bovino et al. (Reference Bovino, Schleicher and Schober2013) and for
![]() $(E_{m}/E_{k})_{sat}$
by Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are plotted with different line styles for a typical range of the turbulence scaling exponent,
$(E_{m}/E_{k})_{sat}$
by Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are plotted with different line styles for a typical range of the turbulence scaling exponent,
![]() $\unicode[STIX]{x1D717}=0.35$
(dotted),
$\unicode[STIX]{x1D717}=0.35$
(dotted),
![]() $0.40$
(solid) and
$0.40$
(solid) and
![]() $0.45$
(dashed). (b,d) Same as left panels, but
$0.45$
(dashed). (b,d) Same as left panels, but
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $(E_{m}/E_{k})_{sat}$
are shown as a function of
$(E_{m}/E_{k})_{sat}$
are shown as a function of
![]() $Re$
for fixed
$Re$
for fixed
![]() $Pm=10$
. The dot-dashed line is a fit to the simulations, yielding a constant saturation level of
$Pm=10$
. The dot-dashed line is a fit to the simulations, yielding a constant saturation level of
![]() $(E_{m}/E_{k})_{sat}=0.05\pm 0.01$
for
$(E_{m}/E_{k})_{sat}=0.05\pm 0.01$
for
![]() $Re>Re_{crit}\equiv Rm_{crit}/Pm=12.9$
and the triple-dot-dashed line shows the result of our modified model for the saturation level originally proposed by Subramanian (Reference Subramanian1999).
$Re>Re_{crit}\equiv Rm_{crit}/Pm=12.9$
and the triple-dot-dashed line shows the result of our modified model for the saturation level originally proposed by Subramanian (Reference Subramanian1999).
3.3.2.1 Dependence on magnetic Prandtl number:
In the left-hand panel of figure 6 we see that
![]() $\unicode[STIX]{x1D6E4}$
first increases strongly with
$\unicode[STIX]{x1D6E4}$
first increases strongly with
![]() $Pm$
for
$Pm$
for
![]() $Pm\lesssim 1$
. For
$Pm\lesssim 1$
. For
![]() $Pm\gtrsim 1$
it keeps increasing, but more slowly. The analytic and semi-analytic models by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) and Bovino et al. (Reference Bovino, Schleicher and Schober2013) both predict an increasing growth rate with
$Pm\gtrsim 1$
it keeps increasing, but more slowly. The analytic and semi-analytic models by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) and Bovino et al. (Reference Bovino, Schleicher and Schober2013) both predict an increasing growth rate with
![]() $Pm$
. These models are shown for three different turbulence scaling exponents,
$Pm$
. These models are shown for three different turbulence scaling exponents,
![]() $\unicode[STIX]{x1D717}=0.35$
(dotted lines),
$\unicode[STIX]{x1D717}=0.35$
(dotted lines),
![]() $\unicode[STIX]{x1D717}=0.40$
(solid lines) and
$\unicode[STIX]{x1D717}=0.40$
(solid lines) and
![]() $\unicode[STIX]{x1D717}=0.45$
(dashed lines) in (3.1). We note that the case with a turbulence scaling exponent
$\unicode[STIX]{x1D717}=0.45$
(dashed lines) in (3.1). We note that the case with a turbulence scaling exponent
![]() $\unicode[STIX]{x1D717}=0.45$
(the dashed lines) is the most appropriate here, because the turbulence in all our simulations is supersonic with Mach numbers in the range 4–11, for which previous high-resolution numerical simulations are consistent with
$\unicode[STIX]{x1D717}=0.45$
(the dashed lines) is the most appropriate here, because the turbulence in all our simulations is supersonic with Mach numbers in the range 4–11, for which previous high-resolution numerical simulations are consistent with
![]() $\unicode[STIX]{x1D717}\approx 0.45$
(Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010). The purely analytical solution of the Kazantsev equation by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) yields power laws for
$\unicode[STIX]{x1D717}\approx 0.45$
(Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010). The purely analytical solution of the Kazantsev equation by Schober et al. (Reference Schober, Schleicher, Bovino and Klessen2012a
) yields power laws for
![]() $Rm>Rm_{crit}$
. However, the semi-analytic solution by Bovino et al. (Reference Bovino, Schleicher and Schober2013) yields a sharp cutoff for
$Rm>Rm_{crit}$
. However, the semi-analytic solution by Bovino et al. (Reference Bovino, Schleicher and Schober2013) yields a sharp cutoff for
![]() $Pm\lesssim 1$
, closer to the results of our 3-D MHD simulations.
$Pm\lesssim 1$
, closer to the results of our 3-D MHD simulations.
The theoretical predictions are qualitatively consistent with the MHD simulations. Quantitative discrepancies arise because the theoretical models assume zero helicity,
![]() $\unicode[STIX]{x1D6FF}$
-correlation of the turbulence in time and do not distinguish solenoidal and compressible modes in the turbulent velocity field. Finite time correlations, however, do not seem to affect the Kazantsev model significantly (Bhat & Subramanian Reference Bhat and Subramanian2014). We therefore conclude that one needs to distinguish between the solenoidal and compressible modes in future dynamo theories, because the dynamo is primarily driven by solenoidal modes and the amount of vorticity strongly depends on the driving and Mach number of the turbulence (Mee & Brandenburg Reference Mee and Brandenburg2006; Federrath et al.
Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
, see § 2).
$\unicode[STIX]{x1D6FF}$
-correlation of the turbulence in time and do not distinguish solenoidal and compressible modes in the turbulent velocity field. Finite time correlations, however, do not seem to affect the Kazantsev model significantly (Bhat & Subramanian Reference Bhat and Subramanian2014). We therefore conclude that one needs to distinguish between the solenoidal and compressible modes in future dynamo theories, because the dynamo is primarily driven by solenoidal modes and the amount of vorticity strongly depends on the driving and Mach number of the turbulence (Mee & Brandenburg Reference Mee and Brandenburg2006; Federrath et al.
Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
, see § 2).
The saturation level as a function of
![]() $Pm$
is shown in the bottom left-hand panel of figure 6. It increases with
$Pm$
is shown in the bottom left-hand panel of figure 6. It increases with
![]() $Pm$
similar to the growth rate and is also well converged with increasing numerical resolution. For
$Pm$
similar to the growth rate and is also well converged with increasing numerical resolution. For
![]() $Pm\gtrsim 10$
,
$Pm\gtrsim 10$
,
![]() $(E_{m}/E_{k})_{sat}$
seems to become independent of
$(E_{m}/E_{k})_{sat}$
seems to become independent of
![]() $Pm$
(and thus independent of
$Pm$
(and thus independent of
![]() $Rm$
, because we have constant
$Rm$
, because we have constant
![]() $Re=1600$
here). The theoretical predictions for
$Re=1600$
here). The theoretical predictions for
![]() $(E_{m}/E_{k})_{sat}$
from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are shown in the low-
$(E_{m}/E_{k})_{sat}$
from Schober et al. (Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) are shown in the low-
![]() $Pm$
and high-
$Pm$
and high-
![]() $Pm$
limits – as for the growth rate,
$Pm$
limits – as for the growth rate,
![]() $\unicode[STIX]{x1D717}=0.45$
is the most relevant case for this comparison. The analytic prediction agrees qualitatively with the results of the MHD simulations, but similar to the limitations of the theories for the growth rate, more work is needed to incorporate the mode mixture (solenoidal versus compressive) in the saturation models.
$\unicode[STIX]{x1D717}=0.45$
is the most relevant case for this comparison. The analytic prediction agrees qualitatively with the results of the MHD simulations, but similar to the limitations of the theories for the growth rate, more work is needed to incorporate the mode mixture (solenoidal versus compressive) in the saturation models.
Brandenburg (Reference Brandenburg2014) performed similar simulations and investigated the saturation level, but in the subsonic regime of turbulence (with
![]() ${\mathcal{M}}\sim 0.1$
), while here we study Mach 10 MHD turbulence. Brandenburg (Reference Brandenburg2014) found that
${\mathcal{M}}\sim 0.1$
), while here we study Mach 10 MHD turbulence. Brandenburg (Reference Brandenburg2014) found that
![]() $(E_{m}/E_{k})_{sat}$
is independent of
$(E_{m}/E_{k})_{sat}$
is independent of
![]() $Pm$
for fixed
$Pm$
for fixed
![]() $Rm$
. Here instead, we show that
$Rm$
. Here instead, we show that
![]() $(E_{m}/E_{k})_{sat}$
increases with
$(E_{m}/E_{k})_{sat}$
increases with
![]() $Pm$
for fixed
$Pm$
for fixed
![]() $Re=1600$
, which implies that
$Re=1600$
, which implies that
![]() $(E_{m}/E_{k})_{sat}$
grows with
$(E_{m}/E_{k})_{sat}$
grows with
![]() $Rm$
for
$Rm$
for
![]() $Pm\lesssim 10$
. This is qualitatively consistent with the simulations (e.g. model X3 versus Y7) in Brandenburg (Reference Brandenburg2014).
$Pm\lesssim 10$
. This is qualitatively consistent with the simulations (e.g. model X3 versus Y7) in Brandenburg (Reference Brandenburg2014).
3.3.2.2 Dependence on kinematic Reynolds number:
The right-hand panels of figure 6 show the growth rate and saturation level as a function of kinematic Reynolds number
![]() $Re$
. Similar to the dependence on
$Re$
. Similar to the dependence on
![]() $Pm$
, we find a nonlinear increase in
$Pm$
, we find a nonlinear increase in
![]() $\unicode[STIX]{x1D6E4}$
with
$\unicode[STIX]{x1D6E4}$
with
![]() $Re$
, which is qualitatively reproduced by the semi-analytic solution of the Kazantsev equation in Bovino et al. (Reference Bovino, Schleicher and Schober2013). However, the critical Reynolds number for dynamo action is much lower in the MHD simulations than predicted by the theoretical models, which may have the same reasons as the discrepancy found for the dependence on
$Re$
, which is qualitatively reproduced by the semi-analytic solution of the Kazantsev equation in Bovino et al. (Reference Bovino, Schleicher and Schober2013). However, the critical Reynolds number for dynamo action is much lower in the MHD simulations than predicted by the theoretical models, which may have the same reasons as the discrepancy found for the dependence on
![]() $Pm$
, i.e. the lack of distinction of mixed turbulence modes in the Kazantsev model.
$Pm$
, i.e. the lack of distinction of mixed turbulence modes in the Kazantsev model.
The top panels of figure 6 show that the growth rate (
![]() $\unicode[STIX]{x1D6E4}$
) depends on both
$\unicode[STIX]{x1D6E4}$
) depends on both
![]() $Pm$
and
$Pm$
and
![]() $Re$
. To take both dependences into account and to determine the critical magnetic Reynolds number for dynamo action, we perform fits with the empirical model function,
$Re$
. To take both dependences into account and to determine the critical magnetic Reynolds number for dynamo action, we perform fits with the empirical model function,
using the fit parameters
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FE}$
, which are related to the critical magnetic Reynolds number
$\unicode[STIX]{x1D6FE}$
, which are related to the critical magnetic Reynolds number
![]() $Rm_{crit}=\exp \left(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FD}\right)$
. From the fits with (3.2) to all our simulations we find that dynamo action is suppressed for
$Rm_{crit}=\exp \left(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6FD}\right)$
. From the fits with (3.2) to all our simulations we find that dynamo action is suppressed for
![]() $Rm<Rm_{crit}=129_{-31}^{+43}$
in highly compressible, supersonic MHD turbulence. Our result for
$Rm<Rm_{crit}=129_{-31}^{+43}$
in highly compressible, supersonic MHD turbulence. Our result for
![]() $Rm_{crit}$
in the supersonic simulations is significantly higher than
$Rm_{crit}$
in the supersonic simulations is significantly higher than
![]() $Rm_{crit}$
measured in subsonic, incompressible turbulence by Haugen et al. (Reference Haugen, Brandenburg and Dobler2004a
), who found
$Rm_{crit}$
measured in subsonic, incompressible turbulence by Haugen et al. (Reference Haugen, Brandenburg and Dobler2004a
), who found
![]() $Rm_{crit}\approx 20$
–
$Rm_{crit}\approx 20$
–
![]() $40$
for
$40$
for
![]() $Pm\gtrsim 1$
. It is also higher than in mildly compressible turbulence, where
$Pm\gtrsim 1$
. It is also higher than in mildly compressible turbulence, where
![]() $Rm_{crit}\approx 50$
for
$Rm_{crit}\approx 50$
for
![]() $Pm=5$
and
$Pm=5$
and
![]() ${\mathcal{M}}\approx 2$
(Haugen et al.
Reference Haugen, Brandenburg and Mee2004b
). The reason for the higher
${\mathcal{M}}\approx 2$
(Haugen et al.
Reference Haugen, Brandenburg and Mee2004b
). The reason for the higher
![]() $Rm_{crit}$
compared to incompressible turbulence could be the more sheet-like than vortex-like structure of supersonic turbulence (Boldyrev Reference Boldyrev2002; Schmidt et al.
Reference Schmidt, Federrath and Klessen2008; Federrath et al.
Reference Federrath, Klessen and Schmidt2009) and the reduced fraction of solenoidal modes (Mee & Brandenburg Reference Mee and Brandenburg2006; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010, Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
, see § 2). The difference of the MHD simulations compared to the Kazantsev models is primarily in
$Rm_{crit}$
compared to incompressible turbulence could be the more sheet-like than vortex-like structure of supersonic turbulence (Boldyrev Reference Boldyrev2002; Schmidt et al.
Reference Schmidt, Federrath and Klessen2008; Federrath et al.
Reference Federrath, Klessen and Schmidt2009) and the reduced fraction of solenoidal modes (Mee & Brandenburg Reference Mee and Brandenburg2006; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010, Reference Federrath, Chabrier, Schober, Banerjee, Klessen and Schleicher2011a
, see § 2). The difference of the MHD simulations compared to the Kazantsev models is primarily in
![]() $Rm_{crit}$
. Bovino et al. (Reference Bovino, Schleicher and Schober2013) predicted a much higher
$Rm_{crit}$
. Bovino et al. (Reference Bovino, Schleicher and Schober2013) predicted a much higher
![]() $Rm_{crit}\approx 4100$
for
$Rm_{crit}\approx 4100$
for
![]() $\unicode[STIX]{x1D717}=0.45$
. However, fits to their theoretical model yield
$\unicode[STIX]{x1D717}=0.45$
. However, fits to their theoretical model yield
![]() $\unicode[STIX]{x1D6FD}=0.11$
–
$\unicode[STIX]{x1D6FD}=0.11$
–
![]() $0.19$
, which is in agreement with the range found in our MHD simulations (
$0.19$
, which is in agreement with the range found in our MHD simulations (
![]() $\unicode[STIX]{x1D6FD}=0.141\pm 0.004$
). This demonstrates that the discrepancy between the simulations and the Kazantsev model is primarily in the critical magnetic Reynolds number, while the qualitative behaviour (determined by the
$\unicode[STIX]{x1D6FD}=0.141\pm 0.004$
). This demonstrates that the discrepancy between the simulations and the Kazantsev model is primarily in the critical magnetic Reynolds number, while the qualitative behaviour (determined by the
![]() $\unicode[STIX]{x1D6FD}$
parameter) is reproduced in the Kazantsev model.
$\unicode[STIX]{x1D6FD}$
parameter) is reproduced in the Kazantsev model.
The saturation level shown in figure 6(d) is consistent with a constant level of
![]() $(E_{m}/E_{k})_{sat}=0.05\pm 0.01$
for
$(E_{m}/E_{k})_{sat}=0.05\pm 0.01$
for
![]() $Re>Re_{crit}\equiv Rm_{crit}/Pm=12.9$
. Given our measurement of
$Re>Re_{crit}\equiv Rm_{crit}/Pm=12.9$
. Given our measurement of
![]() $Rm_{crit}=129$
, we can compute the theoretical prediction by Subramanian (Reference Subramanian1999) for the saturation level,
$Rm_{crit}=129$
, we can compute the theoretical prediction by Subramanian (Reference Subramanian1999) for the saturation level,
![]() $(E_{m}/E_{k})_{sat}=(3/2)(L/u_{turb})\unicode[STIX]{x1D70F}^{-1}Rm_{crit}^{-1}\approx 0.01$
. This is significantly smaller than our simulation result, assuming that
$(E_{m}/E_{k})_{sat}=(3/2)(L/u_{turb})\unicode[STIX]{x1D70F}^{-1}Rm_{crit}^{-1}\approx 0.01$
. This is significantly smaller than our simulation result, assuming that
![]() $\unicode[STIX]{x1D70F}=t_{ed}=L/u_{turb}$
is the turbulent crossing time on the largest scales of the system. However, Subramanian noted that the time scale
$\unicode[STIX]{x1D70F}=t_{ed}=L/u_{turb}$
is the turbulent crossing time on the largest scales of the system. However, Subramanian noted that the time scale
![]() $\unicode[STIX]{x1D70F}$
is an ‘unknown model parameter’. A more appropriate time scale for saturation may be the eddy-turnover time scale on the viscous scale,
$\unicode[STIX]{x1D70F}$
is an ‘unknown model parameter’. A more appropriate time scale for saturation may be the eddy-turnover time scale on the viscous scale,
![]() $\ell _{\unicode[STIX]{x1D708}}=LRe^{-1/(\unicode[STIX]{x1D717}+1)}$
, for a given turbulent velocity scaling following (3.1), because this is where the field saturates first. We find
$\ell _{\unicode[STIX]{x1D708}}=LRe^{-1/(\unicode[STIX]{x1D717}+1)}$
, for a given turbulent velocity scaling following (3.1), because this is where the field saturates first. We find
![]() $\unicode[STIX]{x1D70F}(\ell _{\unicode[STIX]{x1D708}})=\ell _{\unicode[STIX]{x1D708}}/v(\ell _{\unicode[STIX]{x1D708}})=t_{ed}Re^{(\unicode[STIX]{x1D717}-1)/(\unicode[STIX]{x1D717}+1)}$
and with
$\unicode[STIX]{x1D70F}(\ell _{\unicode[STIX]{x1D708}})=\ell _{\unicode[STIX]{x1D708}}/v(\ell _{\unicode[STIX]{x1D708}})=t_{ed}Re^{(\unicode[STIX]{x1D717}-1)/(\unicode[STIX]{x1D717}+1)}$
and with
![]() $Re=Re_{crit}=12.9_{-3.1}^{+4.3}$
, we obtain
$Re=Re_{crit}=12.9_{-3.1}^{+4.3}$
, we obtain
![]() $(E_{m}/E_{k})_{sat}=0.035\pm 0.005$
for a typical range of the velocity scaling exponent
$(E_{m}/E_{k})_{sat}=0.035\pm 0.005$
for a typical range of the velocity scaling exponent
![]() $\unicode[STIX]{x1D717}=0.4\pm 0.1$
from molecular cloud observations (e.g. Larson Reference Larson1981; Ossenkopf & Mac Low Reference Ossenkopf and Mac Low2002; Heyer & Brunt Reference Heyer and Brunt2004; Roman-Duval et al.
Reference Roman-Duval, Federrath, Brunt, Heyer, Jackson and Klessen2011) and simulations of supersonic turbulence (Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Schmidt et al.
Reference Schmidt, Federrath, Hupp, Kern and Niemeyer2009; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Federrath Reference Federrath2013). The saturation level of our MHD simulations agrees within the uncertainties with our modified version of Subramanian’s saturation model.
$\unicode[STIX]{x1D717}=0.4\pm 0.1$
from molecular cloud observations (e.g. Larson Reference Larson1981; Ossenkopf & Mac Low Reference Ossenkopf and Mac Low2002; Heyer & Brunt Reference Heyer and Brunt2004; Roman-Duval et al.
Reference Roman-Duval, Federrath, Brunt, Heyer, Jackson and Klessen2011) and simulations of supersonic turbulence (Kritsuk et al.
Reference Kritsuk, Norman, Padoan and Wagner2007; Schmidt et al.
Reference Schmidt, Federrath, Hupp, Kern and Niemeyer2009; Federrath et al.
Reference Federrath, Roman-Duval, Klessen, Schmidt and Mac Low2010; Federrath Reference Federrath2013). The saturation level of our MHD simulations agrees within the uncertainties with our modified version of Subramanian’s saturation model.
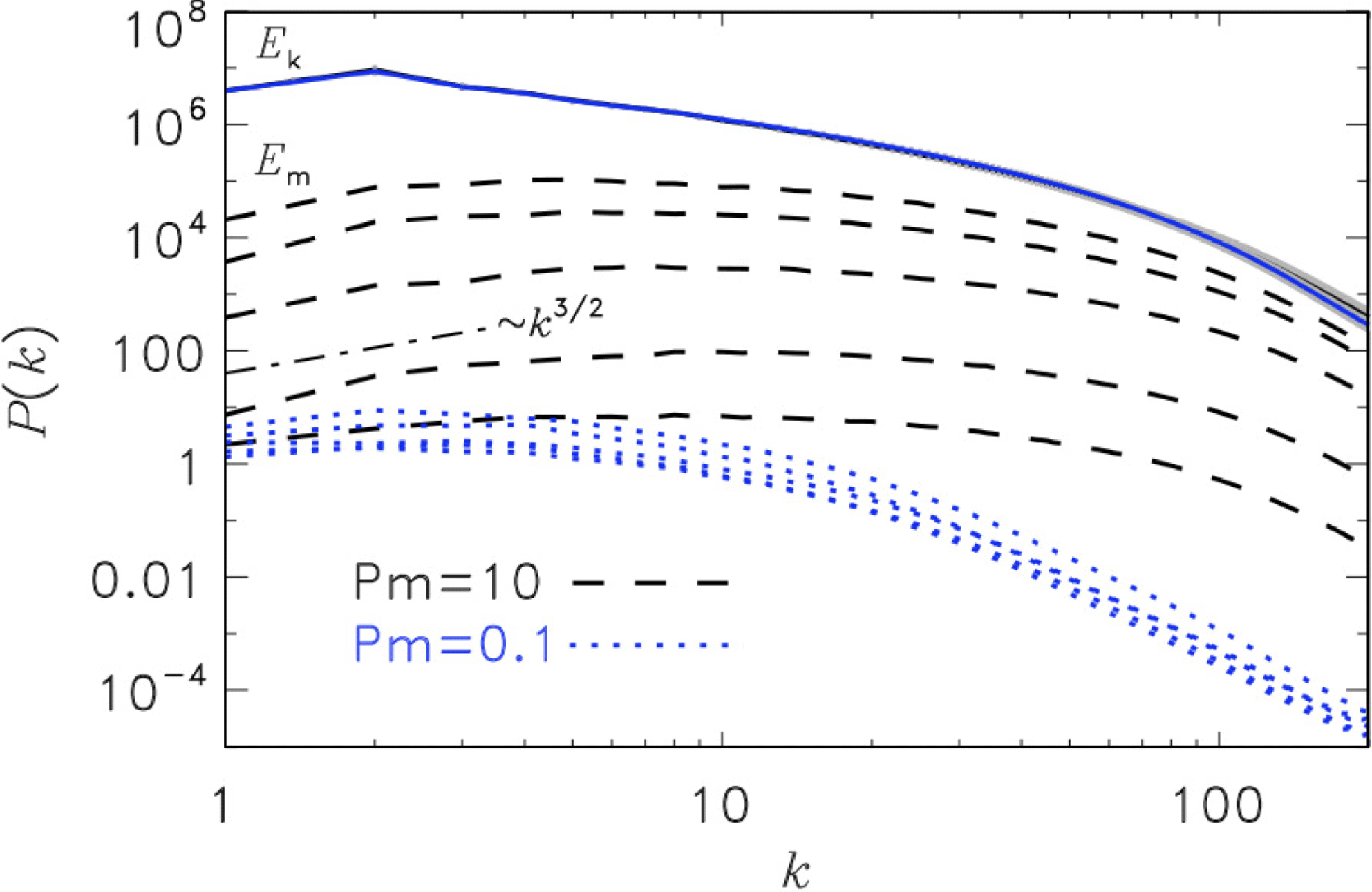
Figure 7. Time evolution of the magnetic energy power spectra for simulations with
![]() $Pm=0.1$
(dotted lines; from bottom to top:
$Pm=0.1$
(dotted lines; from bottom to top:
![]() $t/t_{ed}=2$
,
$t/t_{ed}=2$
,
![]() $5$
,
$5$
,
![]() $10$
,
$10$
,
![]() $15$
,
$15$
,
![]() $18$
) and
$18$
) and
![]() $Pm=10$
(dashed lines; from bottom to top:
$Pm=10$
(dashed lines; from bottom to top:
![]() $t/t_{ed}=2$
,
$t/t_{ed}=2$
,
![]() $5$
,
$5$
,
![]() $10$
,
$10$
,
![]() $15$
,
$15$
,
![]() $24$
). Note that for
$24$
). Note that for
![]() $Pm=10$
, the last magnetic energy spectrum (
$Pm=10$
, the last magnetic energy spectrum (
![]() $t=24\,t_{ed}$
) has just reached saturation on small scales – the
$t=24\,t_{ed}$
) has just reached saturation on small scales – the
![]() $Pm=0.1$
runs did not reach saturation within the limited computing time available because the growth rates are extremely small for this model; cf. figure 6). The Kazantsev spectrum (
$Pm=0.1$
runs did not reach saturation within the limited computing time available because the growth rates are extremely small for this model; cf. figure 6). The Kazantsev spectrum (
![]() $P\propto k^{3/2}$
) is shown as a dash-dotted line for comparison. The solid lines show the time-averaged kinetic energy spectra.
$P\propto k^{3/2}$
) is shown as a dash-dotted line for comparison. The solid lines show the time-averaged kinetic energy spectra.
3.3.3 Evolution of magnetic energy spectra
In figure 7 we show the time evolution of the magnetic energy power spectra in our simulations with
![]() $Pm=0.1$
and
$Pm=0.1$
and
![]() $Pm=10$
and numerical resolution of
$Pm=10$
and numerical resolution of
![]() $1024^{3}$
grid points. They are qualitatively consistent with incompressible dynamo studies (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Mason et al.
Reference Mason, Malyshkin, Boldyrev and Cattaneo2011; Bhat & Subramanian Reference Bhat and Subramanian2013). We see that the power spectra for
$1024^{3}$
grid points. They are qualitatively consistent with incompressible dynamo studies (Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Mason et al.
Reference Mason, Malyshkin, Boldyrev and Cattaneo2011; Bhat & Subramanian Reference Bhat and Subramanian2013). We see that the power spectra for
![]() $Pm=0.1$
dissipate on larger scales (lower
$Pm=0.1$
dissipate on larger scales (lower
![]() $k$
) than the
$k$
) than the
![]() $Pm=10$
spectra, consistent with the theoretical expectation, by a factor of
$Pm=10$
spectra, consistent with the theoretical expectation, by a factor of
![]() $(10/0.1)^{1/(1+\unicode[STIX]{x1D717})}\approx 22$
–
$(10/0.1)^{1/(1+\unicode[STIX]{x1D717})}\approx 22$
–
![]() $27$
for our
$27$
for our
![]() $\unicode[STIX]{x1D717}\approx 0.4$
–
$\unicode[STIX]{x1D717}\approx 0.4$
–
![]() $0.5$
. Even for
$0.5$
. Even for
![]() $Pm=0.1$
, we see the characteristic increase in the magnetic energy on all scales. The magnetic energy spectra roughly follow the Kazantsev spectrum (
$Pm=0.1$
, we see the characteristic increase in the magnetic energy on all scales. The magnetic energy spectra roughly follow the Kazantsev spectrum (
![]() ${\approx}k^{3/2}$
) on large scales (Kazantsev Reference Kazantsev1968; Bhat & Subramanian Reference Bhat and Subramanian2014) in the
${\approx}k^{3/2}$
) on large scales (Kazantsev Reference Kazantsev1968; Bhat & Subramanian Reference Bhat and Subramanian2014) in the
![]() $Pm=10$
case, but we would expect the same to hold in the
$Pm=10$
case, but we would expect the same to hold in the
![]() $Pm=0.1$
case, if our simulations had larger scale separation, i.e. higher numerical resolution. The final spectrum for
$Pm=0.1$
case, if our simulations had larger scale separation, i.e. higher numerical resolution. The final spectrum for
![]() $Pm=10$
has just reached saturation on small scales (approaching the kinetic energy spectrum at high
$Pm=10$
has just reached saturation on small scales (approaching the kinetic energy spectrum at high
![]() $k$
) and continues to grow on larger scales during the nonlinear dynamo phase. The
$k$
) and continues to grow on larger scales during the nonlinear dynamo phase. The
![]() $Pm=0.1$
runs did not have enough time to reach saturation within the limited available compute time (cf. figure 6), but we expect a nonlinear dynamo phase for
$Pm=0.1$
runs did not have enough time to reach saturation within the limited available compute time (cf. figure 6), but we expect a nonlinear dynamo phase for
![]() $Pm<1$
that is qualitatively similar to the
$Pm<1$
that is qualitatively similar to the
![]() $Pm>1$
case.
$Pm>1$
case.
3.4 Summary
In this section we presented a quantitative comparison of the turbulent dynamo in the analytical and semi-analytical Kazantsev models by Subramanian (Reference Subramanian1999), Schober et al. (Reference Schober, Schleicher, Federrath, Klessen and Banerjee2012c
,Reference Schober, Schleicher, Bovino and Klessen
a
, Reference Schober, Schleicher, Federrath, Bovino and Klessen2015) and Bovino et al. (Reference Bovino, Schleicher and Schober2013) with 3-D simulations of supersonic MHD turbulence. We found that the dynamo operates at low and high magnetic Prandtl numbers, but is significantly more efficient for
![]() $Pm>1$
than for
$Pm>1$
than for
![]() $Pm<1$
. The Kazantsev models agree qualitatively with MHD simulations, but not quantitatively. We attribute the quantitative differences to the fact that the current dynamo theories do not take into account the varying mixture of solenoidal and compressible modes in the velocity field in the case of compressible, supersonic plasmas. An extension in this direction is of high priority and would lead to theoretical dynamo models with predictive power for the realistic high Reynolds number regime of many astrophysical plasmas, currently inaccessible to 3-D numerical simulations.
$Pm<1$
. The Kazantsev models agree qualitatively with MHD simulations, but not quantitatively. We attribute the quantitative differences to the fact that the current dynamo theories do not take into account the varying mixture of solenoidal and compressible modes in the velocity field in the case of compressible, supersonic plasmas. An extension in this direction is of high priority and would lead to theoretical dynamo models with predictive power for the realistic high Reynolds number regime of many astrophysical plasmas, currently inaccessible to 3-D numerical simulations.
4 Turbulent magnetic fields in the presence of ordered guide fields
In this section we present new simulations of turbulent plasmas in the presence of a guide field – an ordered magnetic field component. This is relevant to a number of astrophysical applications such as accretion discs where an ordered magnetic field component is often observed along the rotation axis of the disc at a few scale heights above and below the disc mid-plane (Frank et al.
Reference Frank, Ray, Cabrit, Hartigan, Arce, Bacciotti, Bally, Benisty, Eislöffel and Güdel2014). Ordered guide fields are also observed towards molecular clouds in the Milky Way arms (Li et al.
Reference Li, Goodman, Sridharan, Houde, Li, Novak and Tang2014) and in the Galactic Centre cloud G0.253
![]() $+$
0.016 (Pillai et al.
Reference Pillai, Kauffmann, Tan, Goldsmith, Carey and Menten2015; Federrath et al.
Reference Federrath, Rathborne, Longmore, Kruijssen, Bally, Contreras, Crocker, Garay, Jackson and Testi2016b
). We note that the ordered field on a particular scale may actually be part of a turbulent field on much larger scales. However, here we are interested in understanding the amplification and evolution of the turbulent magnetic field (pressure) as a function of the guide-field strength, on the same scale.
$+$
0.016 (Pillai et al.
Reference Pillai, Kauffmann, Tan, Goldsmith, Carey and Menten2015; Federrath et al.
Reference Federrath, Rathborne, Longmore, Kruijssen, Bally, Contreras, Crocker, Garay, Jackson and Testi2016b
). We note that the ordered field on a particular scale may actually be part of a turbulent field on much larger scales. However, here we are interested in understanding the amplification and evolution of the turbulent magnetic field (pressure) as a function of the guide-field strength, on the same scale.
4.1 Simulation parameters and initial conditions
The simulations follow the same equations (2.1)–(2.5) as in the dynamo studies from §§ 2 and 3, but here we add stronger ordered guide fields
![]() $B_{0}$
along the
$B_{0}$
along the
![]() $z$
axis and systematically vary the strength of
$z$
axis and systematically vary the strength of
![]() $B_{0}$
. We fix the driving of the turbulence to solenoidal driving (
$B_{0}$
. We fix the driving of the turbulence to solenoidal driving (
![]() $\unicode[STIX]{x1D701}=1$
in (2.6) and (2.7)) and we keep the average energy injection rate of the turbulence constant, resulting in a roughly constant Mach number
$\unicode[STIX]{x1D701}=1$
in (2.6) and (2.7)) and we keep the average energy injection rate of the turbulence constant, resulting in a roughly constant Mach number
![]() ${\mathcal{M}}=10$
for all simulations. We use normalised, dimensionless values of all basic variables, i.e. a mean density
${\mathcal{M}}=10$
for all simulations. We use normalised, dimensionless values of all basic variables, i.e. a mean density
![]() $\unicode[STIX]{x1D70C}_{0}=1$
, sound speed
$\unicode[STIX]{x1D70C}_{0}=1$
, sound speed
![]() $c_{s}=1$
and box length
$c_{s}=1$
and box length
![]() $L=1$
. This gives a constant total mass
$L=1$
. This gives a constant total mass
![]() $M=1$
and a turbulent box crossing time
$M=1$
and a turbulent box crossing time
![]() $t_{ed}=L/(2{\mathcal{M}}c_{s})=0.05$
. We set the kinematic viscosity to
$t_{ed}=L/(2{\mathcal{M}}c_{s})=0.05$
. We set the kinematic viscosity to
![]() $\unicode[STIX]{x1D708}=3.33\times 10^{-3}$
and the magnetic diffusivity to
$\unicode[STIX]{x1D708}=3.33\times 10^{-3}$
and the magnetic diffusivity to
![]() $\unicode[STIX]{x1D702}=1.67\times 10^{-3}$
, which gives a kinematic Reynolds number of
$\unicode[STIX]{x1D702}=1.67\times 10^{-3}$
, which gives a kinematic Reynolds number of
![]() $Re=L{\mathcal{M}}c_{s}/(2\unicode[STIX]{x1D708})=1500$
and magnetic Reynolds number of
$Re=L{\mathcal{M}}c_{s}/(2\unicode[STIX]{x1D708})=1500$
and magnetic Reynolds number of
![]() $Rm=L{\mathcal{M}}c_{s}/(2\unicode[STIX]{x1D702})=3000$
. Thus, the magnetic Prandtl number is fixed to
$Rm=L{\mathcal{M}}c_{s}/(2\unicode[STIX]{x1D702})=3000$
. Thus, the magnetic Prandtl number is fixed to
![]() $Pm=Rm/Re=2$
. Each simulation was run with a numerical resolution of
$Pm=Rm/Re=2$
. Each simulation was run with a numerical resolution of
![]() $256^{3}$
grid points, but we have also tested a few cases with
$256^{3}$
grid points, but we have also tested a few cases with
![]() $512^{3}$
grid cells and found convergence of our results.
$512^{3}$
grid cells and found convergence of our results.
We run a total of 14 simulations. The ordered guide field (
![]() $B_{0}$
) is varied over approximately five orders of magnitude from
$B_{0}$
) is varied over approximately five orders of magnitude from
![]() $1.2\times 10^{-2}$
to
$1.2\times 10^{-2}$
to
![]() $7.1\times 10^{2}$
, which yields Alfvén Mach numbers with respect to the guide field in the range
$7.1\times 10^{2}$
, which yields Alfvén Mach numbers with respect to the guide field in the range
![]() ${\mathcal{M}}_{A,0}={\mathcal{M}}c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}/B_{0}=0.05$
–
${\mathcal{M}}_{A,0}={\mathcal{M}}c_{s}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}/B_{0}=0.05$
–
![]() $3000$
, i.e. covering the full range from sub-Alfvénic to super-Alfvénic turbulence. Since the simulation domain is periodic, the guide-field strength remains globally constant throughout the whole simulation box because of magnetic-flux conservation. The basic simulation parameters and the derived turbulent magnetic field strengths (
$3000$
, i.e. covering the full range from sub-Alfvénic to super-Alfvénic turbulence. Since the simulation domain is periodic, the guide-field strength remains globally constant throughout the whole simulation box because of magnetic-flux conservation. The basic simulation parameters and the derived turbulent magnetic field strengths (
![]() $B_{turb}$
) are listed in table 3.
$B_{turb}$
) are listed in table 3.
Table 3. List of turbulence simulations with different guide-field strength (
![]() $B_{0}$
).
$B_{0}$
).
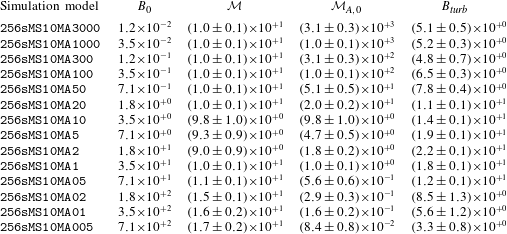
4.2 Results and discussion
As for the simulation models in §§ 2 and 3, we evolve the simulations in table 3 until they reach a converged state in the turbulent magnetic field component (
![]() $B_{turb}$
). Figure 8 shows
$B_{turb}$
). Figure 8 shows
![]() $B_{turb}$
as a function of
$B_{turb}$
as a function of
![]() $B_{0}$
. We find the remarkable result that although we varied
$B_{0}$
. We find the remarkable result that although we varied
![]() $B_{0}$
over five orders of magnitude,
$B_{0}$
over five orders of magnitude,
![]() $B_{turb}$
only varies by a factor of
$B_{turb}$
only varies by a factor of
![]() ${\sim}10$
. Our measurements of
${\sim}10$
. Our measurements of
![]() $B_{turb}$
are listed in the last column of table 3.
$B_{turb}$
are listed in the last column of table 3.
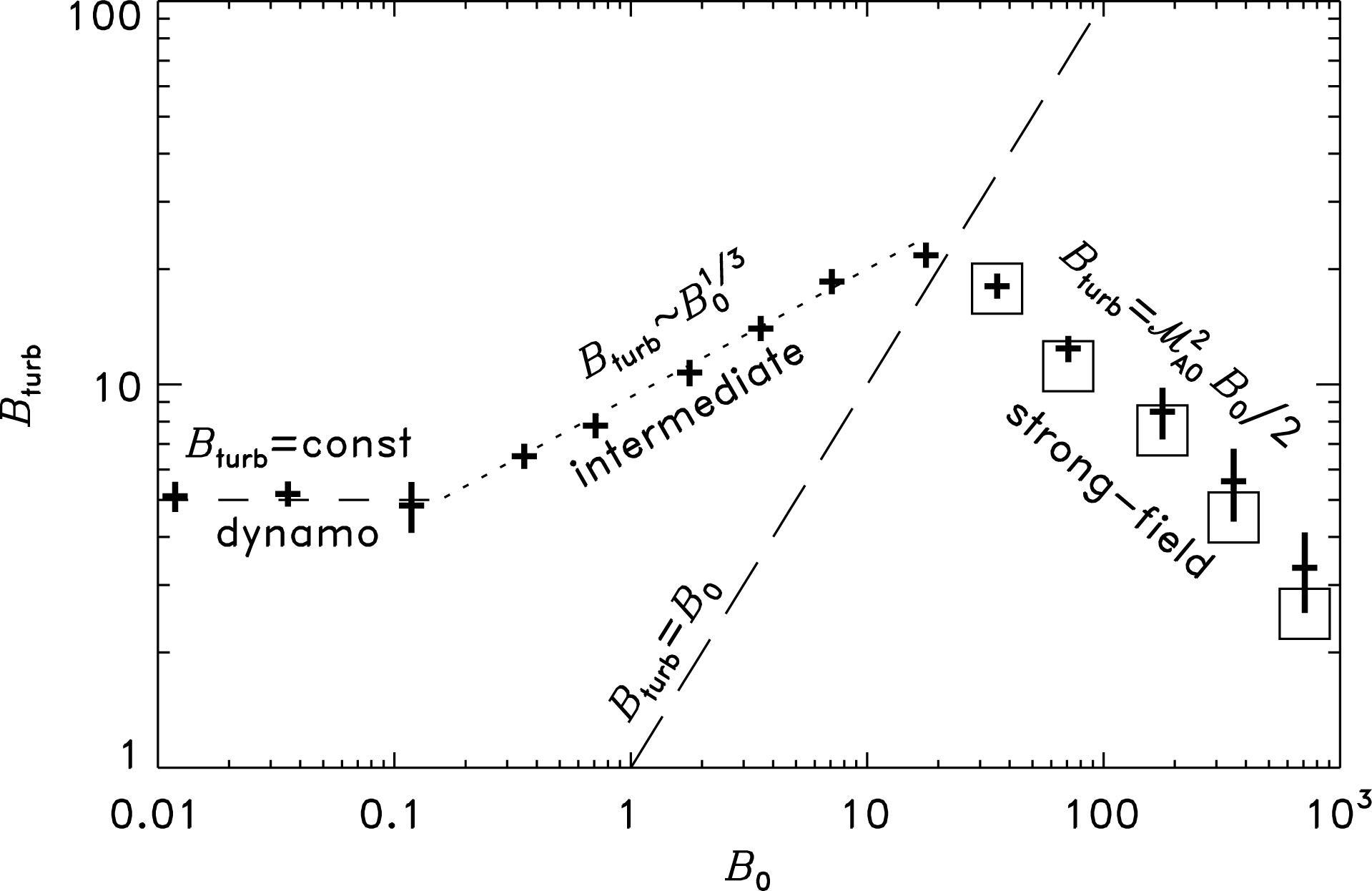
Figure 8. Turbulent (un-ordered) magnetic field (
![]() $B_{turb}$
) as a function of (ordered) magnetic guide field (
$B_{turb}$
) as a function of (ordered) magnetic guide field (
![]() $B_{0}$
) from the simulations (crosses with 1
$B_{0}$
) from the simulations (crosses with 1
![]() $\unicode[STIX]{x1D70E}$
error bars) listed in table 3. We can distinguish three regimes: (i) the dynamo regime for weak
$\unicode[STIX]{x1D70E}$
error bars) listed in table 3. We can distinguish three regimes: (i) the dynamo regime for weak
![]() $B_{0}$
, (ii) the intermediate regime and (iii) the strong guide-field regime. The dashed and dotted lines indicate fits of
$B_{0}$
, (ii) the intermediate regime and (iii) the strong guide-field regime. The dashed and dotted lines indicate fits of
![]() $B_{turb}$
for the dynamo regime and the intermediate regime, respectively. The boxes show the theoretical estimate of
$B_{turb}$
for the dynamo regime and the intermediate regime, respectively. The boxes show the theoretical estimate of
![]() $B_{turb}$
in the strong-field regime (4.10). The long-dashed line shows
$B_{turb}$
in the strong-field regime (4.10). The long-dashed line shows
![]() $B_{turb}=B_{0}$
, which separates the intermediate from the strong-field regime.
$B_{turb}=B_{0}$
, which separates the intermediate from the strong-field regime.
We identify three different regions in figure 8. First, for low guide fields, we find
![]() $B_{turb}=\text{const}$
. This is the ‘dynamo regime’. Second, in the ‘intermediate regime’ we find that
$B_{turb}=\text{const}$
. This is the ‘dynamo regime’. Second, in the ‘intermediate regime’ we find that
![]() $B_{turb}$
increases with
$B_{turb}$
increases with
![]() $B_{0}$
as
$B_{0}$
as
![]() $B_{turb}\propto B_{0}^{1/3}$
. Finally, in the third regime – the ‘strong-field regime’ –
$B_{turb}\propto B_{0}^{1/3}$
. Finally, in the third regime – the ‘strong-field regime’ –
![]() $B_{turb}$
decreases with increasing
$B_{turb}$
decreases with increasing
![]() $B_{0}$
and follows the relation
$B_{0}$
and follows the relation
![]() $B_{turb}={\mathcal{M}}_{A,0}^{2}B_{0}/2$
shown by the boxes. The intermediate and strong-field regimes are separated by the line
$B_{turb}={\mathcal{M}}_{A,0}^{2}B_{0}/2$
shown by the boxes. The intermediate and strong-field regimes are separated by the line
![]() $B_{turb}=B_{0}$
. We now derive the theoretical model,
$B_{turb}=B_{0}$
. We now derive the theoretical model,
![]() $B_{turb}={\mathcal{M}}_{A,0}^{2}B_{0}/2$
, for the strong guide-field regime.
$B_{turb}={\mathcal{M}}_{A,0}^{2}B_{0}/2$
, for the strong guide-field regime.
4.3 Theoretical model for the turbulent magnetic field
We provide a simple analytical model for
![]() $B_{turb}$
in the limits of weak and strong guide field, respectively (
$B_{turb}$
in the limits of weak and strong guide field, respectively (
![]() $B_{turb}\gg B_{0}$
and
$B_{turb}\gg B_{0}$
and
![]() $B_{turb}\ll B_{0}$
). We start by separating the magnetic field into an ordered component (
$B_{turb}\ll B_{0}$
). We start by separating the magnetic field into an ordered component (
![]() $B_{0}$
) and an un-ordered, turbulent component (
$B_{0}$
) and an un-ordered, turbulent component (
![]() $B_{turb}$
),
$B_{turb}$
),
Note that the mean field
![]() $\langle B\rangle =B_{0}$
and
$\langle B\rangle =B_{0}$
and
![]() $\langle B_{turb}\rangle =0$
, while the magnetic energy density is proportional to
$\langle B_{turb}\rangle =0$
, while the magnetic energy density is proportional to
![]() $\langle B^{2}\rangle =B_{0}^{2}+\langle B_{turb}^{2}\rangle +2\langle B_{0}B_{turb}\rangle$
.
$\langle B^{2}\rangle =B_{0}^{2}+\langle B_{turb}^{2}\rangle +2\langle B_{0}B_{turb}\rangle$
.
4.3.1 Weak magnetic guide field
The limit of a weak or vanishing guide field is the dynamo limit that we explored in detail in §§ 2 and 3. In the limit
![]() $B_{turb}\gg B_{0}$
, equation (4.2) becomes
$B_{turb}\gg B_{0}$
, equation (4.2) becomes
![]() $B^{2}\approx B_{turb}^{2}$
and thus the turbulent magnetic energy density
$B^{2}\approx B_{turb}^{2}$
and thus the turbulent magnetic energy density
![]() $e_{m}\approx B_{turb}^{2}/(8\unicode[STIX]{x03C0})$
. From the models of dynamo saturation (cf. §§ 2 and 3), we know that the magnetic energy can only reach a fraction
$e_{m}\approx B_{turb}^{2}/(8\unicode[STIX]{x03C0})$
. From the models of dynamo saturation (cf. §§ 2 and 3), we know that the magnetic energy can only reach a fraction
![]() $\unicode[STIX]{x1D716}_{sat}=(E_{m}/E_{k})_{sat}$
of the turbulent kinetic energy because of the back reaction of the field via the Lorentz force. Thus, in the dynamo limit we make the ansatz,
$\unicode[STIX]{x1D716}_{sat}=(E_{m}/E_{k})_{sat}$
of the turbulent kinetic energy because of the back reaction of the field via the Lorentz force. Thus, in the dynamo limit we make the ansatz,
To evaluate this equation for the present case (
![]() $\unicode[STIX]{x1D70C}_{0}=c_{s}=1$
and
$\unicode[STIX]{x1D70C}_{0}=c_{s}=1$
and
![]() ${\mathcal{M}}=10$
; see § 4.1), we take the measured saturation level
${\mathcal{M}}=10$
; see § 4.1), we take the measured saturation level
![]() $\unicode[STIX]{x1D716}_{sat}\approx 0.02$
from the middle panel of figure 4 for solenoidal driving at Mach 10 and find
$\unicode[STIX]{x1D716}_{sat}\approx 0.02$
from the middle panel of figure 4 for solenoidal driving at Mach 10 and find
![]() $B_{turb}\approx 5$
. This is in excellent agreement with the simulations in the dynamo limit shown in figure 8.
$B_{turb}\approx 5$
. This is in excellent agreement with the simulations in the dynamo limit shown in figure 8.
4.3.2 Strong magnetic guide field
In the limit of a strong guide field (
![]() $B_{turb}\ll B_{0}$
), equation (4.2) can be approximated as
$B_{turb}\ll B_{0}$
), equation (4.2) can be approximated as
![]() $B^{2}\approx B_{0}^{2}+2B_{0}B_{turb}$
and the un-ordered (turbulent) magnetic energy density is
$B^{2}\approx B_{0}^{2}+2B_{0}B_{turb}$
and the un-ordered (turbulent) magnetic energy density is
![]() $e_{m}\approx B_{0}B_{turb}/(4\unicode[STIX]{x03C0})$
. We now make the ansatz that this energy is provided by the turbulent kinetic energy via tangling of the ordered field component,
$e_{m}\approx B_{0}B_{turb}/(4\unicode[STIX]{x03C0})$
. We now make the ansatz that this energy is provided by the turbulent kinetic energy via tangling of the ordered field component,
where we have identified the guide-field Alfvén Mach number
![]() ${\mathcal{M}}_{A,0}=u_{turb}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}/B_{0}$
in the last step. Our simulations in figure 8 are in very good agreement with this theoretical relation for the strong guide-field limit (shown as boxes in figure 8).
${\mathcal{M}}_{A,0}=u_{turb}\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{0}}/B_{0}$
in the last step. Our simulations in figure 8 are in very good agreement with this theoretical relation for the strong guide-field limit (shown as boxes in figure 8).
5 Astrophysical implications of strong magnetic fields
We have seen that turbulent magnetic fields can be generated and amplified over a wide range of physical conditions, from subsonic to supersonic plasmas (§ 2), with high or low magnetic Prandtl number (§ 3) and in the presence of a magnetic guide field (§ 4). This means that magnetic fields can potentially play a significant role in various astrophysical systems and we now discuss a few examples.
5.1 Accretion discs and protostellar jets
Magnetic fields play a crucial role for the dynamics of accretion discs through the MRI (Balbus & Hawley Reference Balbus and Hawley1991), which drives turbulence and angular momentum transport, thereby allowing the central star to gain more mass. The structural changes of the disc caused by the MRI may also influence the disc’s potential to fragment and form planets (Bai & Stone Reference Bai and Stone2014). In the earlier phases of protostellar accretion discs, powerful jets and outflows are launched. It is well known that this type of mechanical feedback is caused by the winding up of the magnetic field in the rotating disc (Blandford & Payne Reference Blandford and Payne1982; Lynden-Bell Reference Lynden-Bell2003; Pudritz et al. Reference Pudritz, Ouyed, Fendt and Brandenburg2007; Frank et al. Reference Frank, Ray, Cabrit, Hartigan, Arce, Bacciotti, Bally, Benisty, Eislöffel and Güdel2014; Krumholz et al. Reference Krumholz, Bate, Arce, Dale, Gutermuth, Klein, Li, Nakamura and Zhang2014). Jets and outflows drive turbulence (Nakamura & Li Reference Nakamura and Li2007, Reference Nakamura and Li2011) and reduce the star formation rate by approximately a factor of 2 (Wang et al. Reference Wang, Li, Abel and Nakamura2010; Federrath Reference Federrath2015). They further reduce the average mass of stars by a factor of 3 (Federrath et al. Reference Federrath, Schrön, Banerjee and Klessen2014b ), thus having a strong impact on the initial mass function (IMF) of stars, the origin of which remains one of the biggest open questions in astrophysics (Offner et al. Reference Offner, Clark, Hennebelle, Bastian, Bate, Hopkins, Moraux and Whitworth2014).
5.2 The interstellar medium of galaxies and molecular cloud formation
The importance of magnetic fields for the formation of molecular clouds has been investigated in several works (Passot, Vazquez-Semadeni & Pouquet Reference Passot, Vazquez-Semadeni and Pouquet1995; Hennebelle et al.
Reference Hennebelle, Banerjee, Vázquez-Semadeni, Klessen and Audit2008; Banerjee et al.
Reference Banerjee, Vázquez-Semadeni, Hennebelle and Klessen2009; Heitsch, Stone & Hartmann Reference Heitsch, Stone and Hartmann2009; Vázquez-Semadeni et al.
Reference Vázquez-Semadeni, Banerjee, Gómez, Hennebelle, Duffin and Klessen2011; Seifried et al.
Reference Seifried, Banerjee, Klessen, Duffin and Pudritz2011). Recently, Körtgen & Banerjee (Reference Körtgen and Banerjee2015) find suppression of star formation by moderate magnetic fields of the order of
![]() $3~\unicode[STIX]{x1D707}\text{G}$
, emphasising the role that the magnetic field plays in regulating the formation of stars.
$3~\unicode[STIX]{x1D707}\text{G}$
, emphasising the role that the magnetic field plays in regulating the formation of stars.
A central outstanding problem is to explain and understand the observed relation of magnetic field strength with cloud density (Crutcher Reference Crutcher2012). The observations suggest that the magnetic field strength is fairly constant with values
![]() ${\sim}1{-}10~\unicode[STIX]{x1D707}\text{G}$
for number densities
${\sim}1{-}10~\unicode[STIX]{x1D707}\text{G}$
for number densities
![]() $n\lesssim 100~\text{cm}^{-3}$
. For densities greater than this, the field increases roughly as
$n\lesssim 100~\text{cm}^{-3}$
. For densities greater than this, the field increases roughly as
![]() $B\propto n^{2/3}$
, consistent with simulations (e.g. Padoan & Nordlund Reference Padoan and Nordlund1999; Li, McKee & Klein Reference Li, McKee and Klein2015). The problem, however, is that in order for clouds to be able to form stars, they need to cross from the so-called ‘sub-critical’ regime (where the collapse of gas is entirely suppressed by the magnetic field) into the ‘super-critical’ regime. How exactly this transition occurs is not well understood. Probably some form of magnetic-flux loss is required, because otherwise, clouds that start off sub-critical at low densities (which indeed seems to be the magnetic state of most of the diffuse gas in the galaxy) would stay sub-critical forever and would not form stars.
$B\propto n^{2/3}$
, consistent with simulations (e.g. Padoan & Nordlund Reference Padoan and Nordlund1999; Li, McKee & Klein Reference Li, McKee and Klein2015). The problem, however, is that in order for clouds to be able to form stars, they need to cross from the so-called ‘sub-critical’ regime (where the collapse of gas is entirely suppressed by the magnetic field) into the ‘super-critical’ regime. How exactly this transition occurs is not well understood. Probably some form of magnetic-flux loss is required, because otherwise, clouds that start off sub-critical at low densities (which indeed seems to be the magnetic state of most of the diffuse gas in the galaxy) would stay sub-critical forever and would not form stars.
5.3 Star formation
It was long thought that magnetic fields control the formation of stars in the interstellar medium through ‘ambipolar diffusion’, the slow drift of neutral gas through the ionised gas towards the centre of the clouds, where star formation would occur (Shu, Adams & Lizano Reference Shu, Adams and Lizano1987). In the last decade, this picture has been replaced by a turbulence-regulated theory of star formation (Elmegreen & Scalo Reference Elmegreen and Scalo2004; Mac Low & Klessen Reference Mac Low and Klessen2004; Scalo & Elmegreen Reference Scalo and Elmegreen2004; McKee & Ostriker Reference McKee and Ostriker2007; Hennebelle & Falgarone Reference Hennebelle and Falgarone2012; Padoan et al. Reference Padoan, Federrath, Chabrier, Evans, Johnstone, Jørgensen, McKee and Nordlund2014), where magnetic fields were considered somewhat less important. However, the most recent years have seen a revival of the role of magnetic fields for star formation and for the structure of the interstellar medium. Both supercomputer simulations and observations have contributed to this recent development.
Firstly, observations show that the magnetic energy density is comparable to the turbulent kinetic energy density in the interstellar medium and in some star-forming clouds (Stahler & Palla Reference Stahler and Palla2004). This is reflected in turbulent Alfvén Mach numbers around unity (Heyer & Brunt Reference Heyer and Brunt2012) and strong ordered magnetic fields on cloud scales (Li & Henning Reference Li and Henning2011; Li et al. Reference Li, Blundell, Hedden, Kawamura, Paine and Tong2011, Reference Li, Goodman, Sridharan, Houde, Li, Novak and Tang2014), in the galactic centre (Dotson et al. Reference Dotson, Vaillancourt, Kirby, Dowell, Hildebrand and Davidson2010; Pillai et al. Reference Pillai, Kauffmann, Tan, Goldsmith, Carey and Menten2015; Federrath et al. Reference Federrath, Rathborne, Longmore, Kruijssen, Bally, Contreras, Crocker, Garay, Jackson and Testi2016b ) and on galactic scales (Beck et al. Reference Beck, Brandenburg, Moss, Shukurov and Sokoloff1996; Beck Reference Beck2016).
Secondly, simulations have demonstrated that magnetic pressure reduces fragmentation, such that only approximately half as many stars form in the presence of a typical magnetic field compared to the case without magnetic fields (Federrath & Klessen Reference Federrath and Klessen2012). This means that magnetic fields cannot be ignored for the IMF (Price & Bate Reference Price and Bate2007; Hennebelle & Teyssier Reference Hennebelle and Teyssier2008; Bürzle et al. Reference Bürzle, Clark, Stasyszyn, Greif, Dolag, Klessen and Nielaba2011; Peters et al. Reference Peters, Banerjee, Klessen and Mac Low2011; Hennebelle et al. Reference Hennebelle, Commerçon, Joos, Klessen, Krumholz, Tan and Teyssier2011). Moreover, magnetic pressure slows the formation of stars by about a factor of 2 (Padoan & Nordlund Reference Padoan and Nordlund2011; Federrath & Klessen Reference Federrath and Klessen2012; Federrath Reference Federrath2015). Recent work suggests that strong magnetic guide fields aligned with the gas flow can also have the opposite effect and increase the star formation rate (Zamora-Aviles et al. Reference Zamora-Aviles, Vazquez-Semadeni, Koertgen, Banerjee and Hartmann2016). Current star formation theories only take the un-ordered turbulent magnetic field component into account (Federrath & Klessen Reference Federrath and Klessen2012). Thus, adding to these theories the effects of magnetic tension caused by strong ordered fields is a priority for the near future.
Acknowledgement
The author thanks the two anonymous referees for their comments, which helped to improve this work. The author gratefully acknowledges funding provided by the Australian Research Council’s Discovery Projects (grant DP150104329). The simulations presented in this work used high performance computing resources provided by the Leibniz Rechenzentrum and the Gauss Centre for Supercomputing (grants pr32lo, pr48pi and GCS Large-scale project 10391), the Partnership for Advanced Computing in Europe (PRACE grant pr89mu), the Australian National Computational Infrastructure (grant ek9), and the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia, in the framework of the National Computational Merit Allocation Scheme and the ANU Allocation Scheme. The simulation software FLASH was in part developed by the DOE-supported Flash Center for Computational Science at the University of Chicago.