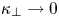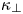1 Introduction
The heat transport in irregular magnetic fields is critical for understanding magnetic confinement experiments and astrophysical systems. Tokamak experiments exploit control coils which produce resonant magnetic perturbations for control of edge localized modes (ELMs) (Evans et al. Reference Evans, Moyer, Watkins, Thomas, Osborne, Boedo, Fenstermacher, Finken, Groebner and Groth2005). Such perturbations must induce a small amount of stochasticization near an edge resonant surface to suppress ELMs without significant degradation of the core confinement. These coils can impart structure in the field outside the last-closed flux surface, resulting in homoclinic tangles (Evans et al. Reference Evans, Moyer, Watkins, Thomas, Osborne, Boedo, Fenstermacher, Finken, Groebner and Groth2005) and stochastic layers (Punjabi et al. Reference Punjabi, Ali, Evans and Boozer2008) which can impact the heat flux deposition at the divertor. Reversed field pinches (RFPs) provides confinement through magnetic fields generated largely by the plasma current. The transport in an RFP is often dominated by parallel diffusion due to stochastic magnetic fields which form due to tearing mode activity (Sarff et al. Reference Sarff, Almagri, Anderson, Borchardt, Carmody, Caspary, Chapman, Den Hartog, Duff and Eilerman2013). The presence of a transport barrier (Biewer et al. Reference Biewer, Forest, Anderson, Fiksel, Hudson, Prager, Sarff, Wright, Brower and Ding2003; Lorenzini et al. Reference Lorenzini, Martines, Piovesan, Terranova, Zanca, Zuin, Alfier, Bonfiglio, Bonomo and Canton2009) can enable the support of a temperature gradient. As stellarators provide confinement with three-dimensional magnetic fields, the impact of non-integrability is critical for heat transport in both the core and divertor regions. For example, the stochastic edge of the Large Helical Device (LHD) features island remnants, stochastic layers and partial barriers. Due to the long connection lengths, both the parallel and perpendicular transport are important for determining the heat flux impacting the divertor plates in a stellarator (Feng et al. Reference Feng, Kobayashi, Lunt and Reiter2011). Stochastic magnetic fields are also expected to exist in several astrophysical environments. For example, the stochasticity of the galactic magnetic field may impact the transport of cosmic rays (Jokipii & Parker Reference Jokipii and Parker1969; Chuvilgin & Ptuskin Reference Chuvilgin and Ptuskin1993).
Given the Hamiltonian nature of magnetic field line flow (Cary & Littlejohn Reference Cary and Littlejohn1983), there are a number of tools from the field of dynamical systems that enable the quantification of the transition to chaos. At the most granular level, the linear stability of a single resonance is quantified through Greene's residue (Greene Reference Greene1979), $R$![]() , where $R < 0$
, where $R < 0$![]() or $R>1$
or $R>1$![]() indicates unstable (hyperbolic or hyperbolic-with-reflection) orbits and $R \in [0,1]$
indicates unstable (hyperbolic or hyperbolic-with-reflection) orbits and $R \in [0,1]$![]() indicates stable (elliptic) orbits. Thus one technique to reduce the stochasticity and island size in a stellarator is through minimization of the magnitude of the residue (Hanson & Cary Reference Hanson and Cary1984; Cary & Hanson Reference Cary and Hanson1986). Similarly, the island width under the small island approximation can be evaluated through a linearization about the island centre (Cary & Hanson Reference Cary and Hanson1991). A shortcoming of these approaches is their limitation to a single resonance rather than a volumetric measure of non-integrability. One can also evaluate the existence or non-existence of a Kolmogorov–Arnold–Moser (KAM) surface to determine the transition to chaos in a given region. To estimate the value of the perturbation required to destroy the last KAM surface between two primary resonances, one may compute the Chirikov overlap criterion (Chirikov Reference Chirikov1979), obtained from the overlap of resonances and their second-order island chains. Greene has also conjectured a procedure for determining the existence of a KAM surface by evaluating the residues of the high-order rational convergents of a given irrational. By examining the stability of the neighbouring periodic orbits to the most stable KAM surface, one can determine the transition to stochasticity (Greene Reference Greene1979; Falcolini & de La Llave Reference Falcolini and de La Llave1992; MacKay Reference MacKay1992). In a similar way, one can evaluate Mather's $\Delta W$
indicates stable (elliptic) orbits. Thus one technique to reduce the stochasticity and island size in a stellarator is through minimization of the magnitude of the residue (Hanson & Cary Reference Hanson and Cary1984; Cary & Hanson Reference Cary and Hanson1986). Similarly, the island width under the small island approximation can be evaluated through a linearization about the island centre (Cary & Hanson Reference Cary and Hanson1991). A shortcoming of these approaches is their limitation to a single resonance rather than a volumetric measure of non-integrability. One can also evaluate the existence or non-existence of a Kolmogorov–Arnold–Moser (KAM) surface to determine the transition to chaos in a given region. To estimate the value of the perturbation required to destroy the last KAM surface between two primary resonances, one may compute the Chirikov overlap criterion (Chirikov Reference Chirikov1979), obtained from the overlap of resonances and their second-order island chains. Greene has also conjectured a procedure for determining the existence of a KAM surface by evaluating the residues of the high-order rational convergents of a given irrational. By examining the stability of the neighbouring periodic orbits to the most stable KAM surface, one can determine the transition to stochasticity (Greene Reference Greene1979; Falcolini & de La Llave Reference Falcolini and de La Llave1992; MacKay Reference MacKay1992). In a similar way, one can evaluate Mather's $\Delta W$![]() , the difference in action between the X and O points associated with a given rational rotation number, $p/q$
, the difference in action between the X and O points associated with a given rational rotation number, $p/q$![]() for integers p and q. If $\Delta W \rightarrow 0$
for integers p and q. If $\Delta W \rightarrow 0$![]() as $p/q$
as $p/q$![]() approaches a given irrational, then the corresponding KAM surface survives (Mather Reference Mather1986). Furthermore, converse KAM theory (Mather Reference Mather1984; MacKay & Percival Reference MacKay and Percival1985; MacKay Reference MacKay2018) provides a sufficient condition for non-existence of a KAM surface by considering the rotation of nearby trajectories with respect to a given foliation.
approaches a given irrational, then the corresponding KAM surface survives (Mather Reference Mather1986). Furthermore, converse KAM theory (Mather Reference Mather1984; MacKay & Percival Reference MacKay and Percival1985; MacKay Reference MacKay2018) provides a sufficient condition for non-existence of a KAM surface by considering the rotation of nearby trajectories with respect to a given foliation.
While each of these techniques may shed light on the existence or non-existence of a KAM surface in a given region, another set of techniques are required to provide insight into the relative impact of non-integrability on the transport in a dynamical system (Meiss Reference Meiss2015). For example, Mather's $\Delta W$![]() is related to the flux of trajectories across a given curve in phase space, providing a bound on the transport (MacKay, Meiss & Percival Reference MacKay, Meiss and Percival1984). One can then partition phase space into subvolumes bounded by KAM surfaces or cantori and model transport between states, such as with a Markov model (Meiss & Ott Reference Meiss and Ott1986).
is related to the flux of trajectories across a given curve in phase space, providing a bound on the transport (MacKay, Meiss & Percival Reference MacKay, Meiss and Percival1984). One can then partition phase space into subvolumes bounded by KAM surfaces or cantori and model transport between states, such as with a Markov model (Meiss & Ott Reference Meiss and Ott1986).
Rather than using nonlinear dynamical surrogates of transport, one could directly evaluate the transport in a given magnetic field line flow. A logical tactic for studying the transport is by introducing a tracer, such as the temperature, $T(\boldsymbol {x})$![]() , which diffuses along the magnetic field subject to some initial condition $T_0(\boldsymbol {x})$
, which diffuses along the magnetic field subject to some initial condition $T_0(\boldsymbol {x})$![]() ,
,
where $\kappa_{\|}$![]() is the parallel diffusion coefficient and $\hat{\boldsymbol{b}}$
is the parallel diffusion coefficient and $\hat{\boldsymbol{b}}$![]() is a unit vector in the direction of the magnetic field. The temperature at a given point, $T(\boldsymbol {x},t)$
is a unit vector in the direction of the magnetic field. The temperature at a given point, $T(\boldsymbol {x},t)$![]() , can be computed by integrating over all contributions of the initial condition along the magnetic field line path (del Castillo-Negrete & Chacon Reference del Castillo-Negrete and Chacon2012). In the steady-state $t \rightarrow \infty$
, can be computed by integrating over all contributions of the initial condition along the magnetic field line path (del Castillo-Negrete & Chacon Reference del Castillo-Negrete and Chacon2012). In the steady-state $t \rightarrow \infty$![]() limit, the temperature becomes constant on magnetic field lines; it is simply the average of the initial condition along the magnetic field line path,
limit, the temperature becomes constant on magnetic field lines; it is simply the average of the initial condition along the magnetic field line path,

where $l$![]() measures length along a field line and L is the total length of integration. Because the temperature is constant along field lines, in a chaotic magnetic field this leads to a fractal-like structure in the temperature profile (Hudson & Breslau Reference Hudson and Breslau2008; del Castillo-Negrete & Chacon Reference del Castillo-Negrete and Chacon2012). In this way, local flattening of the temperature profile can be used as a measure of the local stochasticity.
measures length along a field line and L is the total length of integration. Because the temperature is constant along field lines, in a chaotic magnetic field this leads to a fractal-like structure in the temperature profile (Hudson & Breslau Reference Hudson and Breslau2008; del Castillo-Negrete & Chacon Reference del Castillo-Negrete and Chacon2012). In this way, local flattening of the temperature profile can be used as a measure of the local stochasticity.
While the structure of the magnetic field itself can give rise to transport, in a plasma a non-zero amount of perpendicular transport exists due to the gyromotion, cross-field drifts, collisions and fluctuations. Although the effective perpendicular diffusion can be extremely small in a magnetic confinement device (experimental measurements on the TEXTOR, DIII-D and ASDEX tokamaks indicate $\kappa _{\perp }/\kappa _{\|} \sim 10^{-9}-10^{-7}$![]() (Meskat et al. Reference Meskat, Zohm, Gantenbein, Günter, Maraschek, Suttrop and Yu2001; Hölzl et al. Reference Hölzl, Günter, Classen, Yu and Delabie2009; Bardóczi et al. Reference Bardóczi, Rhodes, Carter, Crocker, Peebles and Grierson2016), where $\kappa _{\perp }$
(Meskat et al. Reference Meskat, Zohm, Gantenbein, Günter, Maraschek, Suttrop and Yu2001; Hölzl et al. Reference Hölzl, Günter, Classen, Yu and Delabie2009; Bardóczi et al. Reference Bardóczi, Rhodes, Carter, Crocker, Peebles and Grierson2016), where $\kappa _{\perp }$![]() is the perpendicular diffusion coefficient), non-zero perpendicular diffusion can substantially alter the heat transport. For example, in the LHD a $\beta = 4.8\,\%$
is the perpendicular diffusion coefficient), non-zero perpendicular diffusion can substantially alter the heat transport. For example, in the LHD a $\beta = 4.8\,\%$![]() (where $\beta$
(where $\beta$![]() is the ratio of the plasma pressure to the magnetic pressure) discharge demonstrated a 32 % reduction in nested magnetic surfaces in comparison with the vacuum magnetic field. However, significant flattening of the temperature profile was not observed (Sakakibara et al. Reference Sakakibara, Watanabe, Suzuki, Narushima, Ohdachi, Nakajima, Watanabe, Garcia, Weller and Toi2008), indicating the relative importance of the perpendicular transport. The perpendicular diffusion becomes even more critical in the stochastic edge, where the collisionality is enhanced.
is the ratio of the plasma pressure to the magnetic pressure) discharge demonstrated a 32 % reduction in nested magnetic surfaces in comparison with the vacuum magnetic field. However, significant flattening of the temperature profile was not observed (Sakakibara et al. Reference Sakakibara, Watanabe, Suzuki, Narushima, Ohdachi, Nakajima, Watanabe, Garcia, Weller and Toi2008), indicating the relative importance of the perpendicular transport. The perpendicular diffusion becomes even more critical in the stochastic edge, where the collisionality is enhanced.
In the steady-state limit, the transport equation (1.1) can be modified to include the effect of perpendicular diffusion
where the parallel gradient is $\boldsymbol {\nabla }_{\|} =\hat {\boldsymbol {b}} \hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla }$![]() and the perpendicular gradient is $\boldsymbol {\nabla }_{\perp } = \boldsymbol {\nabla } - \boldsymbol {\nabla }_{\|}$
and the perpendicular gradient is $\boldsymbol {\nabla }_{\perp } = \boldsymbol {\nabla } - \boldsymbol {\nabla }_{\|}$![]() . We will discuss important properties of this anisotropic diffusion equation (ADE) in § 2. The relative importance of the structure of the magnetic field on transport can then be quantified by comparing the parallel diffusion,
. We will discuss important properties of this anisotropic diffusion equation (ADE) in § 2. The relative importance of the structure of the magnetic field on transport can then be quantified by comparing the parallel diffusion,
with the perpendicular diffusion,
where $V$![]() is the volume of the domain of interest. In this way, the non-integrability of the magnetic field can be quantified by its impact on the transport in a volume rather than through the analysis of individual resonances or the existence of a given KAM surface. This allows us to define an effective volume of perpendicular diffusion in § 3, which we conjecture converges to the effective volume of non-integrability in the limit $\kappa _{\perp } \rightarrow 0$
is the volume of the domain of interest. In this way, the non-integrability of the magnetic field can be quantified by its impact on the transport in a volume rather than through the analysis of individual resonances or the existence of a given KAM surface. This allows us to define an effective volume of perpendicular diffusion in § 3, which we conjecture converges to the effective volume of non-integrability in the limit $\kappa _{\perp } \rightarrow 0$![]() . In § 4 we present the numerical methods used to solve the diffusion equation and the model field used for our calculations. In §§ 5 and 6 we perform calculations of the transport in the presence of a single island chain and a strongly chaotic layer to justify our metric. We then apply the metric to a critical chaotic layer created from resonances of different mode numbers in § 7. We then conclude in § 8.
. In § 4 we present the numerical methods used to solve the diffusion equation and the model field used for our calculations. In §§ 5 and 6 we perform calculations of the transport in the presence of a single island chain and a strongly chaotic layer to justify our metric. We then apply the metric to a critical chaotic layer created from resonances of different mode numbers in § 7. We then conclude in § 8.
2 Properties of the anisotropic diffusion equation
The ADE can be expressed as
with the diffusion tensor
where the perpendicular, $\kappa _{\perp }$![]() , and parallel, $\kappa _{\|}$
, and parallel, $\kappa _{\|}$![]() , diffusion coefficients are taken to be constants. We compute solutions to (2.1) in an annular volume $\varOmega$
, diffusion coefficients are taken to be constants. We compute solutions to (2.1) in an annular volume $\varOmega$![]() bounded by two toroidal surfaces, $S_{-}$
bounded by two toroidal surfaces, $S_{-}$![]() and $S_{+}$
and $S_{+}$![]() with constant Dirichlet boundary conditions $T_{-}$
with constant Dirichlet boundary conditions $T_{-}$![]() and $T_{+}$
and $T_{+}$![]() .
.
2.1 Ellipticity
We note that $\boldsymbol {\kappa }$![]() is positive–definite for $\kappa _{\perp } > 0$
is positive–definite for $\kappa _{\perp } > 0$![]() and $\kappa _{\|} \ge \kappa _{\perp }$
and $\kappa _{\|} \ge \kappa _{\perp }$![]() since
since
for all $\boldsymbol {\nabla } T \ne 0$![]() . (While the assumption $\kappa _{\|} \ge \kappa _{\perp }$
. (While the assumption $\kappa _{\|} \ge \kappa _{\perp }$![]() is not necessary for ellipticity, it is sufficient according to (2.3) and not too restrictive since we are interested in strong anisotropy, $\kappa _{\|}\gg \kappa _{\perp }$
is not necessary for ellipticity, it is sufficient according to (2.3) and not too restrictive since we are interested in strong anisotropy, $\kappa _{\|}\gg \kappa _{\perp }$![]() .) We can furthermore see that the anisotropic diffusion operator is elliptic, as it can be expressed as
.) We can furthermore see that the anisotropic diffusion operator is elliptic, as it can be expressed as
Ellipticity of the anisotropic diffusion operator (2.1) follows from the symmetric positive– definiteness of the tensor which multiplies the second derivatives, $\kappa _{ij}$![]() . Ellipticity implies the existence of a maximum principle (Appendix A),
. Ellipticity implies the existence of a maximum principle (Appendix A),
The corresponding statement also holds for the minimum. In words, the maximum (minimum) temperature must be obtained on the boundary. Furthermore, no local minima or maxima can occur within $\varOmega$![]() . As a further consequence of ellipticity, the topology of the isotherms is constrained (Appendix B). Specifically, an isotherm cannot enclose a net volume, but instead must link the domain toroidal and poloidally as the boundaries (with the possible addition of a handle).
. As a further consequence of ellipticity, the topology of the isotherms is constrained (Appendix B). Specifically, an isotherm cannot enclose a net volume, but instead must link the domain toroidal and poloidally as the boundaries (with the possible addition of a handle).
2.2 Variational principle
The ADE can be obtained (Helander, Hudson & Paul Reference Helander, Hudson and Paul2021) from a variational principle involving the functional
The first variation of $\mathcal {W}$![]() with respect to $T$
with respect to $T$![]() is computed to be
is computed to be
upon application of the boundary condition $\delta T \rvert _{\partial \varOmega } = 0$![]() . Thus stationary points of $\mathcal {W}$
. Thus stationary points of $\mathcal {W}$![]() with respect to $T$
with respect to $T$![]() correspond to solutions of (2.1). We can now compute the second variations as
correspond to solutions of (2.1). We can now compute the second variations as
We note that $\delta ^2 \mathcal {W}[\delta T,\delta T] \ge 0$![]() under the assumption that $\kappa _{\perp }<\kappa _{\|}$
under the assumption that $\kappa _{\perp }<\kappa _{\|}$![]() . Therefore, $\mathcal {W}$
. Therefore, $\mathcal {W}$![]() is a convex function, implying that any stationary point of $\mathcal {W}$
is a convex function, implying that any stationary point of $\mathcal {W}$![]() is a global minimum. We will refer to the functional $\mathcal {W}$
is a global minimum. We will refer to the functional $\mathcal {W}$![]() that appears in this variational principle as the diffusion integral
that appears in this variational principle as the diffusion integral
as it is related to the entropy production functional (Hameiri & Bhattacharjee Reference Hameiri and Bhattacharjee1987). Thus the temperature profile minimizes the entropy production subject to the boundary conditions.
We note that the total diffusion is related to the heat flux through the boundaries
through
where $\boldsymbol {q} = -\kappa _{\|} \boldsymbol {\nabla }_{\|}T - \kappa _{\perp } \boldsymbol {\nabla }_{\perp } T$![]() and $\hat {\boldsymbol {n}}$
and $\hat {\boldsymbol {n}}$![]() is the unit normal oriented in the direction from $S_-$
is the unit normal oriented in the direction from $S_-$![]() to $S_+$
to $S_+$![]() . This relation follows from
. This relation follows from

Thus the total diffusion quantifies the heat flux required to support a given temperature gradient across a volume. In this work we will consider $T_+$![]() and $T_-$
and $T_-$![]() to be fixed such that $D$
to be fixed such that $D$![]() measures the required heat flux to support the prescribed temperature gradient. Since the perpendicular transport is relatively insensitive to the structure of the field, we can assess the impact of non-integrability on the transport through the local parallel diffusion
measures the required heat flux to support the prescribed temperature gradient. Since the perpendicular transport is relatively insensitive to the structure of the field, we can assess the impact of non-integrability on the transport through the local parallel diffusion
in comparison with the local perpendicular diffusion,
3 The effective volume of parallel diffusion
Motivated by comparing $d_{\|}$![]() to $d_{\perp }$
to $d_{\perp }$![]() in order to determine the impact of non-integrability on transport, we propose the following metric:
in order to determine the impact of non-integrability on transport, we propose the following metric:

where $\varTheta$![]() is the Heaviside step function. In words, $\mathcal {V}_{\text {PD}}$
is the Heaviside step function. In words, $\mathcal {V}_{\text {PD}}$![]() measures the fraction of volume over which the local parallel transport is larger than the perpendicular transport. While one could imagine many ways in which to compare the parallel and perpendicular diffusion, the above definition is easy to interpret as it is a positive scalar in $[0,1]$
measures the fraction of volume over which the local parallel transport is larger than the perpendicular transport. While one could imagine many ways in which to compare the parallel and perpendicular diffusion, the above definition is easy to interpret as it is a positive scalar in $[0,1]$![]() .
.
While the definition of $\mathcal {V}_{\text {PD}}$![]() is not intrinsic to the field structure as it depends on $\kappa _{\perp }/\kappa _{\|}$
is not intrinsic to the field structure as it depends on $\kappa _{\perp }/\kappa _{\|}$![]() , we can infer general trends in the limit of small $\kappa _{\perp }/\kappa _{\|}$
, we can infer general trends in the limit of small $\kappa _{\perp }/\kappa _{\|}$![]() . In the limit of an integrable magnetic field with sufficiently small $\kappa _{\perp }$
. In the limit of an integrable magnetic field with sufficiently small $\kappa _{\perp }$![]() , the isotherms will largely coincide with magnetic surfaces, $|\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } T|$
, the isotherms will largely coincide with magnetic surfaces, $|\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } T|$![]() will be relatively small, and thus the local parallel transport will be negligible. Thus $\mathcal {V}_{\text {PD}}$
will be relatively small, and thus the local parallel transport will be negligible. Thus $\mathcal {V}_{\text {PD}}$![]() will be small in the limit of integrability. Since the topology of the isotherms is constrained, isotherms will not be able to completely align to the structure of the field in regions of non-integrability, and $|\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } T|$
will be small in the limit of integrability. Since the topology of the isotherms is constrained, isotherms will not be able to completely align to the structure of the field in regions of non-integrability, and $|\hat {\boldsymbol {b}} \boldsymbol {\cdot } \boldsymbol {\nabla } T|$![]() will be consequently larger, as measured by $\mathcal {V}_{\text {PD}}$
will be consequently larger, as measured by $\mathcal {V}_{\text {PD}}$![]() .
.
We can consider the metric $\mathcal {V}_{\text {PD}}$![]() to be a ‘diffusive’ analogue of a metric based on converse KAM theory. With a converse KAM approach, the non-existence of an invariant torus at a given point in phase space is determined from the rotation of nearby trajectories with respect to a chosen foliation. This allows one to determine regions of phase space over which invariant surfaces do not exist with the topology of the chosen foliation, i.e. a given class of tori (MacKay & Percival Reference MacKay and Percival1985; MacKay Reference MacKay2018). Similarly, by comparing the local parallel and perpendicular diffusion, we can assess whether a given region of physical space is ‘effectively non-integrable’ (indicated by enhanced parallel diffusion) with respect to its impact on the transport. This assessment similarly depends on the topology of the isotherms, which foliate the volume. Since the isotherms must link the domain as the boundaries do, the ADE similarly provides an assessment of the non-integrability with respect to a limited class of tori. For instance, an island chain will impact the parallel transport if the boundary surfaces are chosen to have the same topology as the unperturbed Hamiltonian, given that isotherms cannot have the same linking as the island. If instead the boundary surfaces have the same linking as the surfaces within the island chain, the parallel transport will not be impacted.
to be a ‘diffusive’ analogue of a metric based on converse KAM theory. With a converse KAM approach, the non-existence of an invariant torus at a given point in phase space is determined from the rotation of nearby trajectories with respect to a chosen foliation. This allows one to determine regions of phase space over which invariant surfaces do not exist with the topology of the chosen foliation, i.e. a given class of tori (MacKay & Percival Reference MacKay and Percival1985; MacKay Reference MacKay2018). Similarly, by comparing the local parallel and perpendicular diffusion, we can assess whether a given region of physical space is ‘effectively non-integrable’ (indicated by enhanced parallel diffusion) with respect to its impact on the transport. This assessment similarly depends on the topology of the isotherms, which foliate the volume. Since the isotherms must link the domain as the boundaries do, the ADE similarly provides an assessment of the non-integrability with respect to a limited class of tori. For instance, an island chain will impact the parallel transport if the boundary surfaces are chosen to have the same topology as the unperturbed Hamiltonian, given that isotherms cannot have the same linking as the island. If instead the boundary surfaces have the same linking as the surfaces within the island chain, the parallel transport will not be impacted.
To assess this metric, we consider two cases for which analytic predictions for the parallel transport can be employed: diffusion across a single island chain (§ 5) and across a strongly chaotic layer (§ 6). In § 7 we then consider a model field for which such prediction is more challenging, namely a critically chaotic field with remnants of island chains and partial barriers.
4 Numerical methods
4.1 Linear solution
We compute the numerical solution to the ADE (2.1)–(2.2) using a Fourier Galerkin discretization in $\theta$![]() and $\zeta$
and $\zeta$![]() and a fourth-order finite-difference radial discretization. The resulting sparse linear system is solved with the PETSc library (Balay et al. Reference Balay, Gropp, McInnes and Smith1997, Reference Balay, Abhyankar, Adams, Brown, Brune, Buschelman, Dalcin, Dener, Eijkhout and Gropp2021a,Reference Balay, Abhyankar, Adams, Brown, Brune, Buschelman, Dalcin, Dener, Eijkhout and Groppb) using the MUMPS package (Amestoy et al. Reference Amestoy, Duff, Koster and L'Excellent2001, Reference Amestoy, Buttari, L'Excellent and Mary2019) to compute the lower-upper $(LU)$
and a fourth-order finite-difference radial discretization. The resulting sparse linear system is solved with the PETSc library (Balay et al. Reference Balay, Gropp, McInnes and Smith1997, Reference Balay, Abhyankar, Adams, Brown, Brune, Buschelman, Dalcin, Dener, Eijkhout and Gropp2021a,Reference Balay, Abhyankar, Adams, Brown, Brune, Buschelman, Dalcin, Dener, Eijkhout and Groppb) using the MUMPS package (Amestoy et al. Reference Amestoy, Duff, Koster and L'Excellent2001, Reference Amestoy, Buttari, L'Excellent and Mary2019) to compute the lower-upper $(LU)$![]() -factorization. Throughout we will normalize calculations such that $T_- = 0$
-factorization. Throughout we will normalize calculations such that $T_- = 0$![]() , $T_+ = 1$
, $T_+ = 1$![]() and $\kappa _{\|} = 1$
and $\kappa _{\|} = 1$![]() .
.
4.2 Model magnetic field
We consider a model Hamiltonian,

which yields the magnetic field,
where $\psi = \bar {\psi } \rho /\bar {\rho }$![]() and $(\rho,\theta,\zeta )$
and $(\rho,\theta,\zeta )$![]() forms an orthogonal coordinate system ($\hat {\boldsymbol {\rho }} \times \hat {\boldsymbol {\theta }} \boldsymbol {\cdot } \hat {\boldsymbol {\zeta }} = 1$
forms an orthogonal coordinate system ($\hat {\boldsymbol {\rho }} \times \hat {\boldsymbol {\theta }} \boldsymbol {\cdot } \hat {\boldsymbol {\zeta }} = 1$![]() ) with $\rho \in [0,\bar {\rho }]$
) with $\rho \in [0,\bar {\rho }]$![]() , $\theta \in [0,2{\rm \pi} )$
, $\theta \in [0,2{\rm \pi} )$![]() , $\zeta \in [0,2{\rm \pi} )$
, $\zeta \in [0,2{\rm \pi} )$![]() , $|\boldsymbol {\nabla } \rho | = 1$
, $|\boldsymbol {\nabla } \rho | = 1$![]() , $|\boldsymbol {\nabla } \theta | = 1/\bar {\rho }$
, $|\boldsymbol {\nabla } \theta | = 1/\bar {\rho }$![]() and $|\boldsymbol {\nabla } \zeta | = 1/L_{\zeta }$
and $|\boldsymbol {\nabla } \zeta | = 1/L_{\zeta }$![]() . We will use the notation $\tilde {\epsilon }_{m,n}(\psi ) = \epsilon _{m,n}\psi (\psi -\bar {\psi })$
. We will use the notation $\tilde {\epsilon }_{m,n}(\psi ) = \epsilon _{m,n}\psi (\psi -\bar {\psi })$![]() to denote the strength of the perturbation modes. In the limit $\epsilon _{m,n} \rightarrow 0$
to denote the strength of the perturbation modes. In the limit $\epsilon _{m,n} \rightarrow 0$![]() we recover an integrable magnetic field lying on surfaces of constant $\rho$
we recover an integrable magnetic field lying on surfaces of constant $\rho$![]() with rotational transform $\iota = \iota ' \psi$
with rotational transform $\iota = \iota ' \psi$![]() and constant shear $\iota '(\psi ) = \iota '$
and constant shear $\iota '(\psi ) = \iota '$![]() . The perturbation is chosen to vanish at the upper ($\rho = \bar {\rho }$
. The perturbation is chosen to vanish at the upper ($\rho = \bar {\rho }$![]() ) and lower ($\rho = 0$
) and lower ($\rho = 0$![]() ) boundaries such that there is no parallel flux into the volume. For all of the following numerical calculations, we will take $\bar {\psi } = \bar {\rho } = L_{\zeta } = \iota ' = 1$
) boundaries such that there is no parallel flux into the volume. For all of the following numerical calculations, we will take $\bar {\psi } = \bar {\rho } = L_{\zeta } = \iota ' = 1$![]() .
.
5 Transport across an island chain
In this section, we consider the relative perpendicular and parallel transport in the presence of a single island chain generated by a resonance $\iota = n/m$![]() . We consider the case in which $\kappa _{\perp }$
. We consider the case in which $\kappa _{\perp }$![]() remains small but non-zero such that perpendicular diffusion competes with parallel diffusion.
remains small but non-zero such that perpendicular diffusion competes with parallel diffusion.
To analyse the behaviour of the transport in such a field, in Appendix C we perform a perturbation analysis in the smallness of the amplitude $\epsilon _{m,n}$![]() . Due to the smallness of $\kappa _{\perp }$
. Due to the smallness of $\kappa _{\perp }$![]() , outside of a small boundary layer of width
, outside of a small boundary layer of width

the perpendicular diffusion becomes unimportant. The solution is evaluated both inside and outside the boundary layer. We conclude that for both the inner and outer solution, the parallel and perpendicular diffusion can only be comparable within the island separatrices when $\mathcal {W}_{m,n}/\mathcal {W}_{{c}} \gtrsim 1$![]() , where the island half-width is
, where the island half-width is

In the limit that $\kappa _{\perp } \rightarrow 0$![]() , $\mathcal {W}_{m,n}/\mathcal {W}_{{c}} \gg 1$
, $\mathcal {W}_{m,n}/\mathcal {W}_{{c}} \gg 1$![]() , and the parallel transport can compete with perpendicular transport throughout the volume within the separatrices. In this sense, an island can be considered unimportant to the transport if
, and the parallel transport can compete with perpendicular transport throughout the volume within the separatrices. In this sense, an island can be considered unimportant to the transport if
In figure 1 we present the numerically computed values of the effective volume (3.1) for a single island chain created with resonance $\epsilon _{2,1}$![]() with varying amplitudes and values of $\kappa _{\perp }$
with varying amplitudes and values of $\kappa _{\perp }$![]() . The critical value, $\epsilon _{2,1}^{\text {crit}} = \sqrt {\kappa _{\perp }}/2$
. The critical value, $\epsilon _{2,1}^{\text {crit}} = \sqrt {\kappa _{\perp }}/2$![]() , predicted for the parallel transport to compete with the perpendicular transport, is indicated by the vertical dashed line. We see that, as expected, when the island is smaller than the critical width $\mathcal {W}_{{c}}$
, predicted for the parallel transport to compete with the perpendicular transport, is indicated by the vertical dashed line. We see that, as expected, when the island is smaller than the critical width $\mathcal {W}_{{c}}$![]() , the computed effective volume vanishes. The point at which $\mathcal {V}_{\text {PD}}$
, the computed effective volume vanishes. The point at which $\mathcal {V}_{\text {PD}}$![]() becomes positive is within an order of magnitude of $\epsilon _{2,1}^{\text {crit}}$
becomes positive is within an order of magnitude of $\epsilon _{2,1}^{\text {crit}}$![]() . For large values of $\epsilon _{2,1}$
. For large values of $\epsilon _{2,1}$![]() , the effective volume approaches the expected scaling of the total volume enclosed by the separatrices, $\mathcal {W}_{2,1} \sim \sqrt {\epsilon _{2,1}}$
, the effective volume approaches the expected scaling of the total volume enclosed by the separatrices, $\mathcal {W}_{2,1} \sim \sqrt {\epsilon _{2,1}}$![]() , shown in orange. At non-zero values of the perpendicular diffusion, the scaling of $\mathcal {V}_{\text {PD}}$
, shown in orange. At non-zero values of the perpendicular diffusion, the scaling of $\mathcal {V}_{\text {PD}}$![]() is shallower than the scaling of the total island width since the entire island chain is not dominated by parallel diffusion.
is shallower than the scaling of the total island width since the entire island chain is not dominated by parallel diffusion.

Figure 1. The numerically computed value of the effective volume (3.1) is shown (blue) for the model field (4.2) with the displayed values of $\epsilon _{2,1}$![]() and $\kappa _{\perp }$
and $\kappa _{\perp }$![]() . Also displayed is the scaling of the island width with $\epsilon _{2,1}$
. Also displayed is the scaling of the island width with $\epsilon _{2,1}$![]() (orange), and the critical value of $\epsilon _{2,1}$
(orange), and the critical value of $\epsilon _{2,1}$![]() for which the parallel transport may compete with perpendicular transport (black). The numerically computed value is predicted to approach the $\epsilon _{2,1}^{1/2}$
for which the parallel transport may compete with perpendicular transport (black). The numerically computed value is predicted to approach the $\epsilon _{2,1}^{1/2}$![]() scaling in the limit $\kappa _{\perp } \rightarrow 0$
scaling in the limit $\kappa _{\perp } \rightarrow 0$![]() ; (a) $\kappa _{\perp } = 10^{-6}$
; (a) $\kappa _{\perp } = 10^{-6}$![]() ,(b) $\kappa _{\perp } = 10^{-7}$
,(b) $\kappa _{\perp } = 10^{-7}$![]() , (c) $\kappa _{\perp } = 10^{-8}$
, (c) $\kappa _{\perp } = 10^{-8}$![]() .
.
In figure 2 we present the isotherms (red) computed with the displayed values of $\kappa _{\perp }$![]() on the Poincaré section of the model magnetic field (4.2) with $\epsilon _{2,1} = 0.008$
on the Poincaré section of the model magnetic field (4.2) with $\epsilon _{2,1} = 0.008$![]() . As $\kappa _{\perp }$
. As $\kappa _{\perp }$![]() decreases, the isotherms conform more strongly to the structure of the magnetic field. We note the presence of isotherms which cut across the island chain at smaller values of $\kappa _{\perp }$
decreases, the isotherms conform more strongly to the structure of the magnetic field. We note the presence of isotherms which cut across the island chain at smaller values of $\kappa _{\perp }$![]() due to the topological restrictions. On the right we display the Poincaré section with colour highlighting the region over which the local parallel diffusion is dominating. The colour scale indicates the ratio of the local parallel to perpendicular transport. The parallel transport is strongest near the X-points, where the misalignment of the isotherms with the local field is the strongest. The parallel transport is relatively weak at the top and bottom of the island chain, where the isotherms are more strongly aligned with the magnetic field and the resonant field is weaker. As $\kappa _{\perp }$
due to the topological restrictions. On the right we display the Poincaré section with colour highlighting the region over which the local parallel diffusion is dominating. The colour scale indicates the ratio of the local parallel to perpendicular transport. The parallel transport is strongest near the X-points, where the misalignment of the isotherms with the local field is the strongest. The parallel transport is relatively weak at the top and bottom of the island chain, where the isotherms are more strongly aligned with the magnetic field and the resonant field is weaker. As $\kappa _{\perp }$![]() decreases, we see the area over which the parallel transport dominates increase as well as its magnitude in comparison with the perpendicular transport.
decreases, we see the area over which the parallel transport dominates increase as well as its magnitude in comparison with the perpendicular transport.

Figure 2. The Poincaré section of the model field (4.2) with $\epsilon _{2,1} = 0.008$![]() is displayed with isotherms (red) on the left computed with the three values of $\kappa _{\perp }$
is displayed with isotherms (red) on the left computed with the three values of $\kappa _{\perp }$![]() displayed. On the right, the Poincaré section is displayed with the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $\kappa _{\perp } = 10^{-6}$
displayed. On the right, the Poincaré section is displayed with the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $\kappa _{\perp } = 10^{-6}$![]() , (c,d) $\kappa _{\perp } = 10^{-7}$
, (c,d) $\kappa _{\perp } = 10^{-7}$![]() , (e, f) $\kappa _{\perp } = 10^{-8}$
, (e, f) $\kappa _{\perp } = 10^{-8}$![]() .
.
6 Transport across a strongly chaotic layer
In this section we consider the relative impact of perpendicular and parallel transport in the presence of strong chaos. We will assume a quasilinear model (Chirikov Reference Chirikov1979; Hazeltine & Meiss Reference Hazeltine and Meiss2003; Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2013) to obtain a parallel diffusion coefficient. We will assume that the parallel transport at a given location will be dominated by nearby resonances within an island width and that the phase of the resonances is decorrelated after one toroidal transit. We assume strong chaos such that the Chirikov island overlap parameter is large,
where $\mathcal {W}_{m,n}$![]() is the island half-width associated with resonances (5.2) and $(\Delta \rho )_{m,n;m',n'}$
is the island half-width associated with resonances (5.2) and $(\Delta \rho )_{m,n;m',n'}$![]() is the distance between the resonances.
is the distance between the resonances.
Under the assumption that the resonances are strongly overlapping but $\epsilon _{m,n}$![]() is sufficiently small that a perturbation analysis is appropriate, the motion in the field can be treated as a random walk
is sufficiently small that a perturbation analysis is appropriate, the motion in the field can be treated as a random walk
with a quasi-linear diffusion coefficient given by

See Appendix D for details. The local parallel transport then scales as

We can estimate $|\boldsymbol {\nabla }_{\perp }^2 T| \sim |\boldsymbol {\nabla }_{\perp }T|/L_{\perp }$![]() for some perpendicular length scale $L_{\perp }$
for some perpendicular length scale $L_{\perp }$![]() . Given the analysis in § 5 and Appendix C, we can note several relevant length scales. Within the boundary layer, $L_{\perp } \sim \mathcal {W}_{{c}}$
. Given the analysis in § 5 and Appendix C, we can note several relevant length scales. Within the boundary layer, $L_{\perp } \sim \mathcal {W}_{{c}}$![]() . Outside a width $\mathcal {W}_{m,n}$
. Outside a width $\mathcal {W}_{m,n}$![]() of a given resonance and outside the boundary layer, $L_{\perp } \sim \bar {\rho }$
of a given resonance and outside the boundary layer, $L_{\perp } \sim \bar {\rho }$![]() . Within a width $\mathcal {W}_{m,n}$
. Within a width $\mathcal {W}_{m,n}$![]() and outside the boundary layer, $L_{\perp } \sim |\rho -\rho _{{r}}|$
and outside the boundary layer, $L_{\perp } \sim |\rho -\rho _{{r}}|$![]() . Given that the resonances are strongly overlapping, the perpendicular temperature gradient will be dominated by nearby resonances. Thus we can estimate $L_{\perp } \lesssim \mathcal {W}_{m,n}$
. Given that the resonances are strongly overlapping, the perpendicular temperature gradient will be dominated by nearby resonances. Thus we can estimate $L_{\perp } \lesssim \mathcal {W}_{m,n}$![]() and,
and,

We conclude that the parallel transport may compete with the perpendicular transport when,

To test the expected scaling, we consider the model field (4.2) with $m = 12$![]() and $n = [2,\ldots,10]$
and $n = [2,\ldots,10]$![]() . We evaluate three strongly chaotic fields with amplitudes $\epsilon _{m,n}$
. We evaluate three strongly chaotic fields with amplitudes $\epsilon _{m,n}$![]() chosen such that the Chirikov parameter (6.1) is 2, $2 \sqrt {2}$
chosen such that the Chirikov parameter (6.1) is 2, $2 \sqrt {2}$![]() and 4. We compute solutions to the ADE for a range of $\kappa _{\perp }$
and 4. We compute solutions to the ADE for a range of $\kappa _{\perp }$![]() . The effective volume (3.1) is shown in figure 3 along with the critical value of $\kappa _{\perp }$
. The effective volume (3.1) is shown in figure 3 along with the critical value of $\kappa _{\perp }$![]() (vertical dashed) at which the parallel diffusion may compete (6.6). We note that the point at which the effective volume becomes non-zero is within an order of magnitude of that expected from quasilinear theory for each value of the overlap parameter. As $\kappa _{\perp }$
(vertical dashed) at which the parallel diffusion may compete (6.6). We note that the point at which the effective volume becomes non-zero is within an order of magnitude of that expected from quasilinear theory for each value of the overlap parameter. As $\kappa _{\perp }$![]() decreases, the effective volume computed from the three model fields approach each other.
decreases, the effective volume computed from the three model fields approach each other.

Figure 3. The numerically computed value of the effective volume (3.1) is shown for the model field (4.2) with $m=12$![]() resonances with amplitudes chosen to provide strong island overlap (values of the overlap parameter (6.1) are indicated). Also displayed is the critical value of $\kappa _{\perp }$
resonances with amplitudes chosen to provide strong island overlap (values of the overlap parameter (6.1) are indicated). Also displayed is the critical value of $\kappa _{\perp }$![]() for which the parallel transport is predicted to compete with perpendicular transport (vertical dashed).
for which the parallel transport is predicted to compete with perpendicular transport (vertical dashed).
In figure 4 we display the Poincaré section with isotherms (left) and with the parallel-transport-dominated regions highlighted in colour (right). Although the field is strongly chaotic, we note several isotherms near the boundaries which adapt to the $m = 12$![]() structure of the residual island chains. For $\kappa _{\perp } = 10^{-4}$
structure of the residual island chains. For $\kappa _{\perp } = 10^{-4}$![]() , we note only a very small volume over which the parallel transport dominates. As we decrease the value of $\kappa _{\perp }$
, we note only a very small volume over which the parallel transport dominates. As we decrease the value of $\kappa _{\perp }$![]() , we see that the parallel transport dominates over much of the volume contained within the outermost island separatrices and the temperature gradient across the chaotic layer is significantly reduced. We note an $n = 6$
, we see that the parallel transport dominates over much of the volume contained within the outermost island separatrices and the temperature gradient across the chaotic layer is significantly reduced. We note an $n = 6$![]() variation in the structure of the parallel diffusion due to the poloidal dependence of the radial field (4.2). Near the edges of the chaotic layer, the isotherms become strongly shaped in comparison with the relatively flat isotherms in the chaotic layer. Given that the magnitude of the radial field is smaller than the toroidal field by the amplitude of the perturbation, this feature enhances the parallel diffusion near the boundaries of the chaotic layer.
variation in the structure of the parallel diffusion due to the poloidal dependence of the radial field (4.2). Near the edges of the chaotic layer, the isotherms become strongly shaped in comparison with the relatively flat isotherms in the chaotic layer. Given that the magnitude of the radial field is smaller than the toroidal field by the amplitude of the perturbation, this feature enhances the parallel diffusion near the boundaries of the chaotic layer.

Figure 4. The Poincaré section of the model field (4.2) with $m = 12$![]() resonances chosen to provide an overlap parameter (6.1) of 4 is displayed with isotherms (red) on the left for the three values of $\kappa _{\perp }$
resonances chosen to provide an overlap parameter (6.1) of 4 is displayed with isotherms (red) on the left for the three values of $\kappa _{\perp }$![]() displayed. On the right, the Poincaré section is displayed with the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $\kappa _{\perp } = 10^{-4}$
displayed. On the right, the Poincaré section is displayed with the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $\kappa _{\perp } = 10^{-4}$![]() , (c,d) $\kappa _{\perp } = 10^{-5}$
, (c,d) $\kappa _{\perp } = 10^{-5}$![]() , (e, f) $\kappa _{\perp } = 10^{-6}$
, (e, f) $\kappa _{\perp } = 10^{-6}$![]() .
.
7 Transport across a critically chaotic layer
Although simple analytic scalings can be derived in the case of a single island chain or strong chaos, in reality a magnetic field may possess a complicated mixture of KAM surfaces, partial barriers, chaos and island chains. In this case, we can use the metric defined in § 3 to assess the relative impact of non-integrability on the transport through the volume of parallel diffusion.
As a point of comparison, we will consider four marginally chaotic magnetic fields generated by resonances with different poloidal mode numbers. The amplitude of the perturbation will be chosen to achieve critical island overlap with a comparable volume enclosed by the outermost separatrices. For the first field, we choose $n/m = [1/4, 2/4, 3/4]$![]() . Since the resonances are equally spaced with $\Delta \psi = 1/4$
. Since the resonances are equally spaced with $\Delta \psi = 1/4$![]() , we choose the perturbation amplitudes $\epsilon _{m,n}$
, we choose the perturbation amplitudes $\epsilon _{m,n}$![]() such that the associated half-island widths (5.2) are $1/8$
such that the associated half-island widths (5.2) are $1/8$![]() . We similarly consider fields with $n/m = [2/12,\ldots,10/12]$
. We similarly consider fields with $n/m = [2/12,\ldots,10/12]$![]() , $n/m =[3/20,\ldots,17/20]$
, $n/m =[3/20,\ldots,17/20]$![]() , and $n/m = [5/36,\ldots,31/36]$
, and $n/m = [5/36,\ldots,31/36]$![]() with critical island overlap. The separatrices associated with the outermost island chains for each of these model fields are located at $\rho =1/8$
with critical island overlap. The separatrices associated with the outermost island chains for each of these model fields are located at $\rho =1/8$![]() and $\rho = 7/8$
and $\rho = 7/8$![]() such that they have a comparable ‘volume’ of chaos.
such that they have a comparable ‘volume’ of chaos.
If the remnants of the island chains are dominating the transport, we anticipate the parallel transport to dominate when
from (5.3), while if strong chaos is dominating the transport
from (6.6). Since we have chosen $\epsilon _{m,n} \sim 1/m^2$![]() to achieve critical overlap, we expect the parallel transport to be relatively more impactful when $m$
to achieve critical overlap, we expect the parallel transport to be relatively more impactful when $m$![]() is small. In figure 5 we compare the effective volume between the model fields. Since the volume contained within the outermost separatrices differs slightly between the two model fields, we compute the effective volume only for $\rho \in [0.25, 0.75]$
is small. In figure 5 we compare the effective volume between the model fields. Since the volume contained within the outermost separatrices differs slightly between the two model fields, we compute the effective volume only for $\rho \in [0.25, 0.75]$![]() . As anticipated, the $m = 4$
. As anticipated, the $m = 4$![]() resonances produce a larger effective volume of parallel diffusion, and the relative difference between the model fields increases with increasing $\kappa _{\perp }$
resonances produce a larger effective volume of parallel diffusion, and the relative difference between the model fields increases with increasing $\kappa _{\perp }$![]() . To quantify the effect of the field structure on temperature flattening, we also compare the total temperature differential between $\rho = 0.75$
. To quantify the effect of the field structure on temperature flattening, we also compare the total temperature differential between $\rho = 0.75$![]() and $\rho = 0.25$
and $\rho = 0.25$![]() . At large values of $\kappa _{\perp }$
. At large values of $\kappa _{\perp }$![]() , each of the model fields can support a significant temperature gradient, although it is reduced for the $m =4$
, each of the model fields can support a significant temperature gradient, although it is reduced for the $m =4$![]() field.
field.

Figure 5. (a) The effective volume (3.1) is computed for the model field (4.2) with the displayed mode number perturbations with amplitudes $\epsilon _{m,n}$![]() chosen for critical island overlap. The effective volume is computed over a subset of the entire volume, $\rho \in [0.25, 0.75]$
chosen for critical island overlap. The effective volume is computed over a subset of the entire volume, $\rho \in [0.25, 0.75]$![]() . (b) The total temperature difference between $\rho = 0.75$
. (b) The total temperature difference between $\rho = 0.75$![]() and $\rho = 0.25$
and $\rho = 0.25$![]() upon averaging over the angles.
upon averaging over the angles.
As can be seen from figure 6, each of the fields are visually chaotic with secondary island chains as well as stochastic regions. We furthermore note that the magnitude of the parallel transport, in addition to the volume over which it dominates, is considerably larger in the $m = 4$![]() field. For the $m = 36$
field. For the $m = 36$![]() perturbation, we note that the temperature gradient is not markedly reduced in the chaotic layer when $\kappa _{\perp } = 10^{-6}$
perturbation, we note that the temperature gradient is not markedly reduced in the chaotic layer when $\kappa _{\perp } = 10^{-6}$![]() , although all of the flux surfaces are destroyed. Thus while all of the fields would be classified as very far from integrability by traditional measures such as the Chirikov overlap criterion or converse KAM theory, the impact of the magnetic field structure on the overall transport at non-zero $\kappa _{\perp }$
, although all of the flux surfaces are destroyed. Thus while all of the fields would be classified as very far from integrability by traditional measures such as the Chirikov overlap criterion or converse KAM theory, the impact of the magnetic field structure on the overall transport at non-zero $\kappa _{\perp }$![]() is remarkably distinct.
is remarkably distinct.

Figure 6. The ADE is solved for the model field (4.2) with critically overlapping resonances of $m = 4$![]() , $m = 12$
, $m = 12$![]() and $m=36$
and $m=36$![]() with $\kappa _{\perp } = 10^{-6}$
with $\kappa _{\perp } = 10^{-6}$![]() . On the left are the isotherms (red), and on the right is the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $m=4$
. On the left are the isotherms (red), and on the right is the ratio of the parallel (2.13) to perpendicular (2.14) diffusion. The colour scale is set to white where the parallel diffusion is smaller than the perpendicular diffusion; (a,b) $m=4$![]() , (c,d) $m = 12$
, (c,d) $m = 12$![]() , (e, f) $m = 36$
, (e, f) $m = 36$![]() .
.
8 Conclusions
We have proposed a metric, the effective volume of parallel diffusion, which quantifies the fractional volume over which the parallel transport is dominant over the perpendicular transport. This enables one to determine if a magnetic field is sufficiently integrable with regards to its impact on the transport of heat. We validate this metric for two model fields: a single island chain and strongly chaotic layer. We then consider a critically chaotic magnetic field generated by resonances of different mode numbers. We find that even if no KAM surfaces exist, the relative parallel transport can vary widely between these critically chaotic fields, especially at larger values of $\kappa _{\perp }$![]() . This highlights the importance of quantifying non-integrability not only through the stability of a given orbit or the non-existence of a given KAM surface, but through the resulting impact on the transport. We anticipate many applications of this analysis, such as for the optimization of stellarator magnetic fields and analysis of transport in the stochastic edge.
. This highlights the importance of quantifying non-integrability not only through the stability of a given orbit or the non-existence of a given KAM surface, but through the resulting impact on the transport. We anticipate many applications of this analysis, such as for the optimization of stellarator magnetic fields and analysis of transport in the stochastic edge.
As discussed in § 3, our metric appears to be related to the converse KAM approach, which enables a quantification of the volume of phase space that does not contain KAM surfaces of a given foliation. We expect that the effective volume of parallel diffusion might agree with such a calculation in the limit of small perpendicular diffusion. We reserve such a comparison for future publication.
Acknowledgements
The authors would like to acknowledge fruitful discussions with D. Pfefferle, P. Constantin, R. Mackay, T. Drivas, D. Ginsberg and A. Bhattacharjee.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work was supported in part by a grant from the Simons Foundation/SFARI (560651) and by DOE Contract No. DEAC02–76CH03073.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Maximum principle for ADE
We can now prove a maximum principle for the ADE (Fraenkel Reference Fraenkel2000). Let $T$![]() satisfy the ADE. We define a function $w = T + \epsilon e^{K \boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {c}}$
satisfy the ADE. We define a function $w = T + \epsilon e^{K \boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {c}}$![]() for constant scalars $K>0$
for constant scalars $K>0$![]() , $\epsilon >0$
, $\epsilon >0$![]() , and constant vector $\boldsymbol {c}$
, and constant vector $\boldsymbol {c}$![]() . Applying the ADE operator to $w$
. Applying the ADE operator to $w$![]() , we obtain
, we obtain
From the positive definiteness of $\boldsymbol {\kappa }$![]() , we note that $\boldsymbol {c} \boldsymbol {\cdot } \boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {c} \ge \lambda _0 |\boldsymbol {c}|^2$
, we note that $\boldsymbol {c} \boldsymbol {\cdot } \boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {c} \ge \lambda _0 |\boldsymbol {c}|^2$![]() where $\lambda _0>0$
where $\lambda _0>0$![]() is the smallest eigenvalue of $\boldsymbol {\kappa }$
is the smallest eigenvalue of $\boldsymbol {\kappa }$![]() . This yields the inequality
. This yields the inequality
We choose $K > \max _{\varOmega } |(\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {\kappa })\boldsymbol {\cdot } \boldsymbol {c} |/(\lambda _0 |\boldsymbol {c}|^2)$![]() so that $\boldsymbol {\nabla } \boldsymbol {\cdot } (\boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {\nabla } w )>0$
so that $\boldsymbol {\nabla } \boldsymbol {\cdot } (\boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {\nabla } w )>0$![]() .
.
Suppose now that the maximum value of $w$![]() is obtained within the domain, $\varOmega$
is obtained within the domain, $\varOmega$![]() , at a point $\boldsymbol {x}_0$
, at a point $\boldsymbol {x}_0$![]() . This implies that $\boldsymbol {\nabla } w\rvert _{\boldsymbol {x}_0} = 0$
. This implies that $\boldsymbol {\nabla } w\rvert _{\boldsymbol {x}_0} = 0$![]() and the Hessian matrix $\boldsymbol {\nabla } \boldsymbol {\nabla } w \rvert _{\boldsymbol {x}_0}$
and the Hessian matrix $\boldsymbol {\nabla } \boldsymbol {\nabla } w \rvert _{\boldsymbol {x}_0}$![]() is negative semi-definite. This implies that
is negative semi-definite. This implies that
The final inequality follows from expressing $\boldsymbol {\kappa }$![]() in terms of the eigenvalues, $\mu _i$
in terms of the eigenvalues, $\mu _i$![]() , and eigenvectors, $\overrightarrow {\boldsymbol {x}}_i$
, and eigenvectors, $\overrightarrow {\boldsymbol {x}}_i$![]() , of $\boldsymbol {\nabla } \boldsymbol {\nabla } w$
, of $\boldsymbol {\nabla } \boldsymbol {\nabla } w$![]() with $\mu _i \le 0$
with $\mu _i \le 0$![]()
From the positive–definiteness of $\boldsymbol {\kappa }$![]() , we find that $\omega _i>0$
, we find that $\omega _i>0$![]() . We can then note that
. We can then note that

As this is in contradiction with the choice we have made for $K$![]() , we conclude that the maximum of $w$
, we conclude that the maximum of $w$![]() must occur on $\partial \varOmega$
must occur on $\partial \varOmega$![]() and
and
This implies that $\max _{\bar {\varOmega }}T = \max _{\partial \varOmega }T$![]() . Otherwise, we would have $\max _{\varOmega }T = \max _{\partial \varOmega }T + \delta$
. Otherwise, we would have $\max _{\varOmega }T = \max _{\partial \varOmega }T + \delta$![]() for some $\delta > 0$
for some $\delta > 0$![]() . As we are free to choose $\epsilon < \delta /\max _{\partial \varOmega } e^{K \boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {c}}$
. As we are free to choose $\epsilon < \delta /\max _{\partial \varOmega } e^{K \boldsymbol {x} \boldsymbol {\cdot } \boldsymbol {c}}$![]() , this would lead to a contradiction. A similar argument can be constructed to show that the minimum value of $T$
, this would lead to a contradiction. A similar argument can be constructed to show that the minimum value of $T$![]() must occur on the boundary.
must occur on the boundary.
Appendix B. Topology of isotherms
In this appendix, we discuss the possible topology of the isotherms given properties of the ADE.
To begin, we consider the region near the boundaries. We first note that the normal derivative of the temperature must be sign definite on the boundaries unless $T$![]() is constant in $\varOmega$
is constant in $\varOmega$![]() . In other words, $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\nabla } T > 0$
. In other words, $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\nabla } T > 0$![]() on $S_{-}$
on $S_{-}$![]() and $S_{+}$
and $S_{+}$![]() assuming $T_{+} > T_{-}$
assuming $T_{+} > T_{-}$![]() and $\hat {\boldsymbol {n}}$
and $\hat {\boldsymbol {n}}$![]() is oriented in the direction of increasing $\rho$
is oriented in the direction of increasing $\rho$![]() . This result is known as the Hopf lemma (Fraenkel Reference Fraenkel2000). Intuitively, the flux through the boundary cannot change sign since $S_{-}$
. This result is known as the Hopf lemma (Fraenkel Reference Fraenkel2000). Intuitively, the flux through the boundary cannot change sign since $S_{-}$![]() and $S_{+}$
and $S_{+}$![]() are isotherms. As a result, in a small neighbourhood of the boundary $\partial T/\partial \rho \ne 0$
are isotherms. As a result, in a small neighbourhood of the boundary $\partial T/\partial \rho \ne 0$![]() , and isotherms close with the same topology as the boundary. We conclude that at least within a small neighbourhood of $S_{-}$
, and isotherms close with the same topology as the boundary. We conclude that at least within a small neighbourhood of $S_{-}$![]() and $S_{+}$
and $S_{+}$![]() , isotherms must be deformable to the boundaries.
, isotherms must be deformable to the boundaries.
We now argue that the temperature gradient cannot vanish within a subvolume of $\varOmega$![]() if the specified temperature differential $T_{+}-T_{-}$
if the specified temperature differential $T_{+}-T_{-}$![]() is non-zero. To see this, suppose that the temperature is constant within a subvolume, $\mathcal {V}$
is non-zero. To see this, suppose that the temperature is constant within a subvolume, $\mathcal {V}$![]() . We remark that under the assumption that the coefficients appearing in the elliptic problem (2.4), $\boldsymbol {\kappa }$
. We remark that under the assumption that the coefficients appearing in the elliptic problem (2.4), $\boldsymbol {\kappa }$![]() and $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {\kappa }$
and $\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {\kappa }$![]() , are analytic, $T$
, are analytic, $T$![]() must also be analytic due to the ellipticity of the ADE operator. If $T$
must also be analytic due to the ellipticity of the ADE operator. If $T$![]() is analytic and is constant within $\mathcal {V}$
is analytic and is constant within $\mathcal {V}$![]() , this implies that $T$
, this implies that $T$![]() is constant in $\varOmega$
is constant in $\varOmega$![]() . Since such a solution is inconsistent with the boundary conditions, we conclude that the temperature gradient can only vanish on isolated lines, surfaces or points. These must be saddle points given the maximum principle.
. Since such a solution is inconsistent with the boundary conditions, we conclude that the temperature gradient can only vanish on isolated lines, surfaces or points. These must be saddle points given the maximum principle.
We now consider the possible linking of isothermal surfaces (figure 7). Suppose that there exists an isotherm, $\mathcal {S}$![]() , with the linking of a sphere (i.e. does not close toroidally or poloidally) or the linking of an ‘island’ (i.e. closes toroidally or poloidally but not both). In that case, we can integrate the ADE over a volume $\mathcal {V}$
, with the linking of a sphere (i.e. does not close toroidally or poloidally) or the linking of an ‘island’ (i.e. closes toroidally or poloidally but not both). In that case, we can integrate the ADE over a volume $\mathcal {V}$![]() bounded by one of these isotherms, $\mathcal {S} = \partial \mathcal {V}$
bounded by one of these isotherms, $\mathcal {S} = \partial \mathcal {V}$![]()
We note that $\boldsymbol {\nabla } T \propto \hat {\boldsymbol {n}}$![]() and $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\nabla } T$
and $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\nabla } T$![]() is sign definite on $\partial \mathcal {V}$
is sign definite on $\partial \mathcal {V}$![]() . Because $\boldsymbol {\kappa }$
. Because $\boldsymbol {\kappa }$![]() is positive–definite, $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {\nabla } T$
is positive–definite, $\hat {\boldsymbol {n}} \boldsymbol {\cdot } \boldsymbol {\kappa } \boldsymbol {\cdot } \boldsymbol {\nabla } T$![]() will also be sign definite on $\partial \mathcal {V}$
will also be sign definite on $\partial \mathcal {V}$![]() . This leads to a contradiction unless $\boldsymbol {\nabla } T = 0$
. This leads to a contradiction unless $\boldsymbol {\nabla } T = 0$![]() . Given that the temperature gradient cannot vanish within a finite volume, we conclude that the isotherms must link as the boundaries such that they do not enclose a net volume.
. Given that the temperature gradient cannot vanish within a finite volume, we conclude that the isotherms must link as the boundaries such that they do not enclose a net volume.

Figure 7. Possible linking of closed isotherms (blue) which are periodic and do not intersect the boundaries (red); (a) ‘spherical’ (not closed toroidally or poloidally), (b) poloidally closed ‘island’ structure, (c) toroidally closed ‘island’ structure, (d) toroidally and poloidally closed (deformable to boundary) and (e) a toroidally and poloidally closed surface with the addition of a handle.
Now that we have argued that the isotherms must link toroidally and poloidally as the boundaries, we now discuss their topology. We consider an isotherm which links as the boundaries but with the addition of a small handle (figure 7d). Such an isotherm is consistent with the integral condition (B1) as it does not enclose a volume. We conclude that the isotherms must link toroidally and poloidally, with the possible addition of a handle. However, isotherms cannot enclose a net volume, as an ‘island’ or ‘sphere’ structure.
Appendix C. Single island chain analysis
In this appendix we analyse the ADE for the case of a single small island chain, as discussed in § 5. We perform a perturbation analysis in the small parameter $\epsilon = |\chi _1|/|\chi _0| \ll 1$![]() where $\chi _0 = \iota ' \psi ^2/2$
where $\chi _0 = \iota ' \psi ^2/2$![]() and $\chi _1 = \chi - \chi _0$
and $\chi _1 = \chi - \chi _0$![]() . In the limit $\chi = \chi _0$
. In the limit $\chi = \chi _0$![]() , the solution of the ADE is given by,
, the solution of the ADE is given by,
We will call this the unperturbed temperature. In computing the first-order correction, the perturbed temperature, we apply the ansatz $T_1(\rho,\theta,\zeta ) = \hat {T}(\rho ) \cos (m \theta - n \zeta )$![]() . The first-order perturbation to the ADE reads
. The first-order perturbation to the ADE reads
where $\hat {\boldsymbol {b}}_0$![]() and $\hat {\boldsymbol {b}}_1$
and $\hat {\boldsymbol {b}}_1$![]() are the unit vectors in the direction of the magnetic field at $\mathcal {O}(\epsilon ^0)$
are the unit vectors in the direction of the magnetic field at $\mathcal {O}(\epsilon ^0)$![]() and $\mathcal {O}(\epsilon ^1)$
and $\mathcal {O}(\epsilon ^1)$![]() . Applying the ansatz for $T_1$
. Applying the ansatz for $T_1$![]() results in the ordinary differential equation (ODE)
results in the ordinary differential equation (ODE)

where $\mathcal {W}_{m,n}$![]() is the island half-width (5.2). In obtaining the above expression, we focus on a region near the $n/m$
is the island half-width (5.2). In obtaining the above expression, we focus on a region near the $n/m$![]() rational surface such that the unperturbed field strength can be approximated as $|\boldsymbol {B}_0| = (\bar {\psi }/\bar {\rho }^2) (1 + (\iota ' \bar {\psi } \rho /L_{\zeta })^2)^{1/2} \approx (\bar {\psi }/\bar {\rho }^2) (1 + (n \bar {\rho }/(mL_{\zeta }))^2)^{1/2}$
rational surface such that the unperturbed field strength can be approximated as $|\boldsymbol {B}_0| = (\bar {\psi }/\bar {\rho }^2) (1 + (\iota ' \bar {\psi } \rho /L_{\zeta })^2)^{1/2} \approx (\bar {\psi }/\bar {\rho }^2) (1 + (n \bar {\rho }/(mL_{\zeta }))^2)^{1/2}$![]() . Due to the smallness of $\kappa _{\perp }$
. Due to the smallness of $\kappa _{\perp }$![]() , outside of a small boundary layer of width $\mathcal {W}_{{c}}$
, outside of a small boundary layer of width $\mathcal {W}_{{c}}$![]() , the perpendicular diffusion becomes unimportant. We can express the first-order perturbation to the ADE in terms of the layer variable $X = (\rho - \rho _{{r}})/\mathcal {W}_{{c}}$
, the perpendicular diffusion becomes unimportant. We can express the first-order perturbation to the ADE in terms of the layer variable $X = (\rho - \rho _{{r}})/\mathcal {W}_{{c}}$![]() , where $\rho _{{r}} = \bar {\rho }n/(m \iota '\bar {\psi })$
, where $\rho _{{r}} = \bar {\rho }n/(m \iota '\bar {\psi })$![]() is the location of the resonant surface
is the location of the resonant surface

We will analyse the solution both inside and outside of the layer, similar to the analysis in Fitzpatrick (Reference Fitzpatrick1995).
C.1 Inner solution
Inside the boundary layer, the second term in (C4) is unimportant as $\mathcal {W}_{{c}}/\bar {\rho } \ll 1$![]() by assumption. Thus the first and third terms must balance each, allowing us to obtain the scaling for the boundary layer width as (5.1). Balance between the first and last terms yields a scaling for the temperature perturbation as
by assumption. Thus the first and third terms must balance each, allowing us to obtain the scaling for the boundary layer width as (5.1). Balance between the first and last terms yields a scaling for the temperature perturbation as
This matches the scaling in (32) of Fitzpatrick (Reference Fitzpatrick1995). This implies that $|\boldsymbol {\nabla }_{\perp } T_1| \sim (\mathcal {W}_{m,n}/\mathcal {W}_{{c}})^2 |\boldsymbol {\nabla }_{\perp } T_0|$![]() . When $\mathcal {W}_{m,n} \ll \mathcal {W}_{{c}}$
. When $\mathcal {W}_{m,n} \ll \mathcal {W}_{{c}}$![]() , $|\boldsymbol {\nabla }_{\perp } T_0| \gg |\boldsymbol {\nabla }_{\perp } T_1|$
, $|\boldsymbol {\nabla }_{\perp } T_0| \gg |\boldsymbol {\nabla }_{\perp } T_1|$![]() and the ratio of parallel to perpendicular diffusion scales as
and the ratio of parallel to perpendicular diffusion scales as
since $|\boldsymbol {\nabla }_{\|} T_1| \sim \mathcal {W}_\text {c}^{-1} \kappa _{\perp }^{1/2} T_1$![]() . Otherwise, if $\mathcal {W}_{m,n}/\mathcal {W}_{{c}} \gtrsim 1$
. Otherwise, if $\mathcal {W}_{m,n}/\mathcal {W}_{{c}} \gtrsim 1$![]() , the ratio can be $\sim 1$
, the ratio can be $\sim 1$![]() .
.
C.2 Outer solution
Outside of the boundary layer, the perpendicular diffusion can be ignored to a good approximation, and the ADE reduces to
Outside of the island separatrix, we apply a perturbation analysis to obtain
This yields the solution
where the superscript $(0)$![]() indicates the solution which neglects perpendicular diffusion. This matches the scaling of (38) in Fitzpatrick (Reference Fitzpatrick1995). Given (C8), the parallel temperature gradient is negligible in this region if perpendicular diffusion is ignored. Now retaining the perpendicular diffusion terms from (C4), the correction to $\hat {T}(\rho )$
indicates the solution which neglects perpendicular diffusion. This matches the scaling of (38) in Fitzpatrick (Reference Fitzpatrick1995). Given (C8), the parallel temperature gradient is negligible in this region if perpendicular diffusion is ignored. Now retaining the perpendicular diffusion terms from (C4), the correction to $\hat {T}(\rho )$![]() scales as $\hat {T}^{(1)}(\rho )\sim \hat {T}(\rho ) \mathcal {W}_{{c}}^4/(\bar {\rho }^2 (\rho - \rho _{{r}})^2)$
scales as $\hat {T}^{(1)}(\rho )\sim \hat {T}(\rho ) \mathcal {W}_{{c}}^4/(\bar {\rho }^2 (\rho - \rho _{{r}})^2)$![]() , and the parallel diffusion will scale as $|\boldsymbol {\nabla }_{\|} T| \sim \kappa _{\perp }^{1/2} \mathcal {W}_{{c}}^{-2} (\rho - \rho _{{r}}) \hat {T}^{(1)}(\rho )$
, and the parallel diffusion will scale as $|\boldsymbol {\nabla }_{\|} T| \sim \kappa _{\perp }^{1/2} \mathcal {W}_{{c}}^{-2} (\rho - \rho _{{r}}) \hat {T}^{(1)}(\rho )$![]() . Given that $|\boldsymbol {\nabla }_{\perp } T_0| \gg |\boldsymbol {\nabla }_{\perp } T_1|$
. Given that $|\boldsymbol {\nabla }_{\perp } T_0| \gg |\boldsymbol {\nabla }_{\perp } T_1|$![]() in this region, the ratio of the parallel to perpendicular diffusion will have the scaling
in this region, the ratio of the parallel to perpendicular diffusion will have the scaling
Within the island separatrix, (C7) implies that the temperature must be a function of the island flux surfaces. This is not possible unless the temperature is flattened across the island chain given the maximum principle. At non-zero $\kappa _{\perp }$![]() , a finite temperature gradient is allowed. Given that the temperature is flattened within the separatrices if perpendicular diffusion is not included, both the parallel and perpendicular temperature gradients will be driven by $\hat {T}^{(1)}(\rho )$
, a finite temperature gradient is allowed. Given that the temperature is flattened within the separatrices if perpendicular diffusion is not included, both the parallel and perpendicular temperature gradients will be driven by $\hat {T}^{(1)}(\rho )$![]() with scaling given by $|\boldsymbol {\nabla }_{\|} T| \sim \kappa _{\perp }^{1/2} \mathcal {W}_{{c}}^{-2} (\rho - \rho _{{r}})\hat {T}^{(1)}(\rho )$
with scaling given by $|\boldsymbol {\nabla }_{\|} T| \sim \kappa _{\perp }^{1/2} \mathcal {W}_{{c}}^{-2} (\rho - \rho _{{r}})\hat {T}^{(1)}(\rho )$![]() and $|\boldsymbol {\nabla }_{\perp } T| \sim \hat {T}^{(1)}(\rho )/(\rho - \rho _{{r}})$
and $|\boldsymbol {\nabla }_{\perp } T| \sim \hat {T}^{(1)}(\rho )/(\rho - \rho _{{r}})$![]() . This yields the scaling for the ratio of the parallel to perpendicular diffusion as
. This yields the scaling for the ratio of the parallel to perpendicular diffusion as
We conclude that, for the outer solution, the ratio $|\boldsymbol {\nabla }_{\|}T|^2/(\kappa _{\perp }|\boldsymbol {\nabla }_{\perp }T|^2)$![]() can only be $\gtrsim 1$
can only be $\gtrsim 1$![]() if $|\rho -\rho _{{r}}|< \mathcal {W}_{m,n}$
if $|\rho -\rho _{{r}}|< \mathcal {W}_{m,n}$![]() and $\mathcal {W}_{{c}} \ll \mathcal {W}_{m,n}$
and $\mathcal {W}_{{c}} \ll \mathcal {W}_{m,n}$![]() .
.
Appendix D. Strong chaos analysis
In this appendix we analyse the ADE for the case of strong chaos, as discussed in § 6. If we assume that $\epsilon _{m,n}$![]() is sufficiently small, we can linearize the trajectories with respect to the small parameter $\epsilon = |\chi _1|/|\chi _0| \ll 1$
is sufficiently small, we can linearize the trajectories with respect to the small parameter $\epsilon = |\chi _1|/|\chi _0| \ll 1$![]() where $\chi _0 = \iota ' \psi ^2/2$
where $\chi _0 = \iota ' \psi ^2/2$![]() and $\chi _1 = \chi - \chi _0$
and $\chi _1 = \chi - \chi _0$![]()
where $\iota (\psi _0) = \iota ' \psi _0$![]() is the rotational transform associated with the unperturbed Hamiltonian (4.2). The linearized trajectories satisfy
is the rotational transform associated with the unperturbed Hamiltonian (4.2). The linearized trajectories satisfy


and are computed to be


Thus we can see that the resonant terms in $\theta _1(\zeta )$![]() within a width $\mathcal {W}_{m,n}/2$
within a width $\mathcal {W}_{m,n}/2$![]() (5.2) of a given rational surface will be $\mathcal {O}(1/m)$
(5.2) of a given rational surface will be $\mathcal {O}(1/m)$![]() and will thus dominate the evolution. We can then approximate the trajectories as
and will thus dominate the evolution. We can then approximate the trajectories as


where $\varTheta$![]() is the Heaviside step function. In one toroidal period, the flux changes by an amount given by $\Delta \psi \approx 2{\rm \pi} \,{\rm d}\psi _1/{\rm d}\zeta$
is the Heaviside step function. In one toroidal period, the flux changes by an amount given by $\Delta \psi \approx 2{\rm \pi} \,{\rm d}\psi _1/{\rm d}\zeta$![]() and the poloidal angle changes by an amount given by $\Delta \theta \approx 2{\rm \pi} \,{\rm d} \theta _1/{\rm d}\zeta$
and the poloidal angle changes by an amount given by $\Delta \theta \approx 2{\rm \pi} \,{\rm d} \theta _1/{\rm d}\zeta$![]() . We note that the uncertainty in the poloidal angle will be $\mathcal {O}(1)$
. We note that the uncertainty in the poloidal angle will be $\mathcal {O}(1)$![]() if the resonances are strongly overlapping. In this way, with every toroidal period, the poloidal angle will be kicked by an amplitude that depends on the surrounding resonances. We assume that $\theta _0$
if the resonances are strongly overlapping. In this way, with every toroidal period, the poloidal angle will be kicked by an amplitude that depends on the surrounding resonances. We assume that $\theta _0$![]() can, therefore, be treated as a random variable, and we approximate the motion in such a field as a random walk
can, therefore, be treated as a random variable, and we approximate the motion in such a field as a random walk
with a diffusion coefficient given by
where $\langle \cdots \rangle$![]() indicates an average over the possible initial conditions, $\theta _0$
indicates an average over the possible initial conditions, $\theta _0$![]() . The full expression for $D_{\|}$
. The full expression for $D_{\|}$![]() is given in (6.3).
is given in (6.3).