No CrossRef data available.
Article contents
Modulational instability of the interacting electron whistlers and magnetosonic perturbations
Published online by Cambridge University Press: 28 February 2024
Abstract
A modulational instability of nonlinearly interacting electron whistlers and magnetosonic perturbations is studied in the present paper. For typical parameters, there is no modulational instability. However, modulational instability appears in special cases. For example, when the whistler wavenumber is small enough, there is modulational instability. Its growth rate decreases as the angle between the external magnetic field and the perturbed wave's direction increases, while it increases as the whistler wavenumber increases. It is also found that there is no modulational instability when the whistler wavenumber is larger than a critical value ($k_0 > 0.05$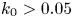 ), in which the perturbed wave frequency increases as the angle between the external magnetic field and the perturbed wave's direction increases when the angle between the external magnetic field and the perturbed wave's direction is large enough. Whereas, the perturbed wave frequency first increases as the whistler wavenumber increases, reaches a peak value and then decreases as whistler wavenumber increases.
), in which the perturbed wave frequency increases as the angle between the external magnetic field and the perturbed wave's direction increases when the angle between the external magnetic field and the perturbed wave's direction is large enough. Whereas, the perturbed wave frequency first increases as the whistler wavenumber increases, reaches a peak value and then decreases as whistler wavenumber increases.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2024. Published by Cambridge University Press





