Article contents
A spherical indentation technique for property evaluation of hyperelastic rubber
Published online by Cambridge University Press: 31 July 2012
Abstract
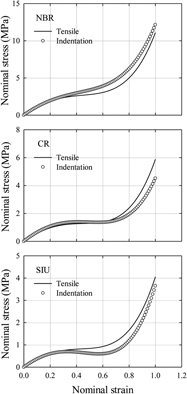
The numerical approach of Lee et al. [Trans. Korean Soc. Mech. Eng., A28, 816–825 (2004)] to spherical indentation technique for property evaluation of hyperelastic rubber is enhanced. The Yeoh model is adopted as the constitutive form of rubber material because it can express well large deformation and cover various deformation modes with a simple form. We first determine the friction coefficient between a rubber specimen and a spherical indenter in a practical viewpoint and perform finite element simulations for a deeper indentation depth than that selected by Lee et al. [Trans. Korean Soc. Mech. Eng., A28, 816–825 (2004)]. An optimal data acquisition spot is selected, which features sufficiently large strain energy density and negligible frictional effect. We improve then two normalized functions mapping an indentation load–displacement curve onto a strain energy density–invariant curve, the latter of which gives the Yeoh model constants. The enhanced spherical indentation approach successfully produces the rubber material properties with an average error of less than 5%. The validity of our developed approach is verified by experimental evaluation of material properties with three kinds of rubber materials.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2012
References
REFERENCES
- 7
- Cited by


