Article contents
Microscale deformation of (001) and (100) rutile single crystals under spherical nanoindentation
Published online by Cambridge University Press: 24 November 2011
Abstract
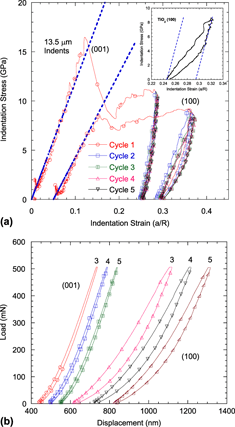
Herein rutile (TiO2) single-crystal surfaces, with (001) and (100) orientations, were indented with hemispherical indenters with radii of 13.5, 5, and 1.4 μm. By converting the load–displacement data to nanoindentation (NI) stress–strain curves, together with microscopic post-indentation observations, we conclude that in the (001) orientation, plastic deformation occurs by the activation of all four {101}<10 > slip systems. In the (100) orientation, only two of the four {101}<10
> slip systems. In the (100) orientation, only two of the four {101}<10 > slip systems, along with {100}<0
> slip systems, along with {100}<0 0> slip, are activated. Because the four {101}<10
0> slip, are activated. Because the four {101}<10 > slip systems in the (001) orientation intersect, the surface is harder and exhibits higher hardening rates after the nucleation of dislocations. The latter are manifested by pop-ins, some of which are large. The pop-in stresses are adequately described by Weibull statistics and were significantly higher for the (001) orientation. The elastic moduli, determined from spherical NI stiffness versus contact radii plots, were 349 ± 5 and 229 ± 4 GPa for (001) and (100) orientations, respectively. Fully spontaneous reversible, stress–strain hysteretic curves—only manifest in the (100) orientation—are attributed to the to-and-fro motion of dislocations comprising incipient kink bands in the {100}<0
> slip systems in the (001) orientation intersect, the surface is harder and exhibits higher hardening rates after the nucleation of dislocations. The latter are manifested by pop-ins, some of which are large. The pop-in stresses are adequately described by Weibull statistics and were significantly higher for the (001) orientation. The elastic moduli, determined from spherical NI stiffness versus contact radii plots, were 349 ± 5 and 229 ± 4 GPa for (001) and (100) orientations, respectively. Fully spontaneous reversible, stress–strain hysteretic curves—only manifest in the (100) orientation—are attributed to the to-and-fro motion of dislocations comprising incipient kink bands in the {100}<0 0> slip system.
0> slip system.
- Type
- Articles
- Information
- Journal of Materials Research , Volume 27 , Issue 1: Focus Issue: Instrumented Indentation , 14 January 2012 , pp. 53 - 63
- Copyright
- Copyright © Materials Research Society 2011
References
REFERENCES
- 11
- Cited by


