Hostname: page-component-84b7d79bbc-5lx2p Total loading time: 0 Render date: 2024-07-29T20:37:58.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of Moore's higher reciprocity law at the prime 2 for real number fields

Published online by Cambridge University Press:  07 January 2008

Xuejun Guo  and
Hourong Qin
Xuejun Guo
Affiliation:
guox@nju.edu.cnDepartment of Mathematics, Nanjing University, Nanjing 210093, The People's Republic of China guox@nju.edu.cnThe Abdus Salam International Center for Theoretical Physics, Trieste, Italy
Hourong Qin
Affiliation:
hrqin@nju.edu.cnDepartment of Mathematics, Nanjing University, Nanjing 210093, The People's Republic of China
Get access

Abstract

Let F be a real number field with r1 real embeddings. In this paper, we prove that the sequence

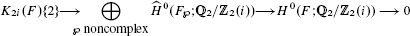
is a complex, where 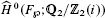are the Tate cohomology groups. Moreover if i ≡ 0, 1, or 2 (mod 4), then it is exact; if i ≡ 3 (mod 4), then the homology group at the second term of this complex is isomorphic to .

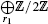Keywords

Moore's reciprocity uniqueness theoremBloch-Lichtenbaum spectral sequenceTate-Poitou duality theorem
Type
Research Article
Information
Journal of K-Theory , Volume 1 , Issue 1 , February 2008 , pp. 185 - 192
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Banaszak, G., Generalization of the Moore exact sequence and the wild kernel for higher K-groups, Compositio Math. 86 (1993), 281–305Google Scholar
2.Kahn, B., Algebraic K-theory and twisted reciprocity laws, K-Theory 30 (2003), 211–240CrossRefGoogle Scholar
3.Levine, M., K-theory and motivic cohomology of schemes, UIUC K-Theory preprints Archives, No. 336Google Scholar
4.Milnor, J., Introduction to algebraic K-theory, Annals of Mathematics Studies 72, Princeton University Press, 1971.Google Scholar
5.Moore, C., Group extensions of p-adic and adelic linear groups, I. H. E. S. Publ. Math. No. 35 (1968), 157–222Google Scholar
6.Rognes, J. and Weibel, C., Two-primary algebraic K-theory of rings of integers in number fields, J. Amer. Math. Soc. 13 (2000) no. 1, 1–54CrossRefGoogle Scholar
7.Tate, J., Duality theorems in Galois cohomology over number fields, 1963 Proc. Internat. Congr. Mathematicians (Stockholm, 1962), pp. 288–295Google Scholar