Introduction

The effect of liquid water upon the dielectric characteristics of snow has been a puzzle for glaciologists during the last few decades. Several papers dealing with the electrical properties of snow have been published. However, the results for wet snow are not always consistent with one another.

Snow can be treated as a three-component mixture consisting of air, ice, and water. A special case is dry snow which contains no liquid (free) water. The dielectric properties of these constituents are well known, including their frequency dependence (see, for example, Reference HallikainenHallikainen, 1977). Experimental formulae for the complex permittivity of dry snow have also been presented (Reference NyforsNyfors, 1982; Reference Tiuri, Tiuri, Sihvola, Nyfors and HallikainenTiuri and others, 1984). Numerous formulae explaining and predicting the dielectric characteristics of wet snow have been presented. These may be mixing formulae that have the permittivities of air, ice, and water as parameters, or they may even be linearized functions of density and wetness. More rigorous mixing theories take into account the microscopic structure of snow and the liquid water distribution. In this case, the resulting formulae usually contain additional parameters (for example, depolarization factors of the ice and water particles) that are determined by the type of snow. In this paper it is presumed that the effects of ice and water on the permittivity of wet snow can be superposed. In other words, the three-component mixing formula

(1)

is separable in the form

(2)

where ϵ_s is the complex permittivity of snow, ρ is the dry density (see below), and W is the wetness of snow. This means that wet snow is treated as a two-component mixture consisting of dry snow and liquid water. And dry snow is for its part a dielectric mixture of air and ice. There are papers employing this separation approach, for example Reference Ambach and DenothAmbach and Denoth (1972), Reference Denoth and SchittelkopfDenoth and Schittelkopf (1978), Reference Ambach, Denoth and RangoAmbach and Denoth (1980), Reference Denoth, Denoth, Foglar, Weiland, Mätzler, Aebischer, Tiuri and SihvolaMätzler and others (1984), Reference Tiuri, Tiuri, Sihvola, Nyfors and HallikainenTiuri and others (1984); see also Reference Stiles and UlabyStiles and Ulaby (1981).

The first term in Equation (2) is the permittivity of dry snow, the density of which is equal to the “dry density” of the wet snow in question, i.e. the density which the snow sample would have if all the liquid water were replaced by air. Because the dielectric properties of dry snow are fairly well known, the most interesting problem is the increase of the complex permittivity due to the free water, in other words the second term in Equation (2). The difference between the permittivities of wet snow (ϵ_s) and dry snow (ϵ_d)

(3)

is therefore a result of the dielectric mixture of air and water. This mixture gives the increase of the real part of the permittivity of snow. And, because dry snow is practically lossless in comparison with water at microwave frequencies, the whole imaginary part of the dielectric constant of wet snow comes from this mixture.

Dielectric properties of the constituents

The relative permittivity of air is ϵ_air = 1 − j0. At 1 GHz and 0°C the dielectric constant of ice is ϵ_ice = 3.15 − j0.003. Air and ice are also quasi-dispersionless in the microwave range. Therefore the dielectric properties of dry snow obey the high-frequency approximation of the Debye equation, the relaxation frequency being less than 100 kHz. The real part of the permittivity is constant with frequency at microwave wavelengths, and, as has already been noted, the loss factor is negligible. Accordingly, the dispersion characteristics of wet snow originate from the frequency dependence of liquid water.

The complex permittivity of water ϵ_w follows fairly well the Debye equation

(4)

where ϵ_ws is the static dielectric constant of water, ϵ_w∞ is the high-frequency dielectric constant of water, and τ_w is the relaxation time of water. Experimental values for ϵ_w∞ range from 4.5 to 5.5. At 0°C the static permittivity is ϵ_ws ≃ 88 and the relaxation time τ_w ≈ 18 ps.

Therefore the relaxation frequency is around 9 GHz under normal conditions. Hence most dielectric measurements of wet snow are carried out in the low-frequency range. Many snow sensors for determining the permittivity of snow operate near 1 GHz Reference Tiuri, Tiuri, Sihvola and Nyfors(Tiuri and others, 1982; Reference Aebischer and MatzlerAebischer and Mätzler, 1983; Reference Denoth, Denoth, Foglar, Weiland, Mätzler, Aebischer, Tiuri and SihvolaDenoth and others, 1984). In this paper the air–water mixture is therefore discussed considering a frequency of 1 GHz. For calculating the dielectric properties of wet snow at other frequencies from the 1 GHz results, see Reference Tiuri, Tiuri, Sihvola, Nyfors and HallikainenTiuri and others (1984). At 1 GHz and 0°C the relative dielectric constant of water is ϵ_w = 88.0 − j9.79.

In this paper the models explaining the dielectric behaviour of the mixture are divided into two groups. Structure-independent “exponential models” predict the permittivity without recourse to microstructure parameters unlike the “structure-dependent models”.

Exponential models

Mixing formulae

The exponential models give the complex permittivity of the mixture ϵ_mixt as a function of the complex permittivities of its constituents ϵ_i through the equation

(5)

where f_i is the volume fraction of the ith constituent, and . The exponent a is the degree of the model, and = 0 < a ⩽ 1.

Exponential models have been applied to dielectric mixtures by many authors:

a = 1	Brown has presented a formula of this kind linearly dependent on the volume fraction Reference Wang and Schmugge(Wang and Schmugge, 1980). Reference FungFung (1982) has also applied it for determining the effective dielectric constant of a vegetated medium.
a = 1/2	Birchak and others have derived this formula for the soil–water mixture Reference Birchak, Birchak, Gardner, Hipp and Victor(Birchak and others, 1974).
a = 0.4	By treating wet snow as a three-component mixture, one can apply the exponential model to the classical results of Reference CummingCumming (1952). The best fit is found by optimizing the parameter a, and the result is a = 0.4.
a = 1/3	This value of the parameter a will lead to a cubic function for the permittivity of two-phase mixtures.

The complex dielectric constant ϵ_m of a two-component mixture in which the other component is air, according to the exponential model, obeys the following formula (obtained directly from Equation (5):

(6)

where ϕ is the volume fraction of the inclusions. Therefore 1 − ϕ is the volume fraction occupied by air. ϵ_i is the complex permittivity of the inclusion material (ϵ_i = ϵ_i′(1 − j tan δ_i) = ϵ_i′ − jϵ_i”).

The following approximation, which assumes that the inclusion material has low losses, will be used:

(7)

The error in this approximation has its maximum value at a = 0.5. For the air–water mixture (ϵ_i = ϵ_w), tan δ_i = 0.111 25 gives (1 − j tan δ_i) ^a = 1.0015 − j0.0555 and 1 − ja tan δ_i = 1 − j0.0556. The error is 0.2%, which is negligible. For the air–ice mixture (ϵ_i = ϵ_ice) the error is still very much smaller.

Applying the approximation to Equation (6) yields

(8)

Therefore

(9)

(10)

Dry snow

From Reference Tiuri, Tiuri, Sihvola, Nyfors and HallikainenTiuri and others (1984), the empirical values for the dielectric constant of dry snow are

(11)

(12)

where ϵ″_ice is the imaginary part of the dielectric constant of ice.

The exponential mixing model can be applied to dry snow conceived as a dielectric mixture of air and ice (with the complex permittivity 3.15(1 − j0.001). When the parameter a is a = 1/2, we have

(13)

(14)

which follows the experimental results fairly well.

The case a = 1/3 leads to the formula of Looyenga for dry snow Reference Stiles and Ulaby(Stiles and Ulaby, 1981):

(15)

which explains the real part of the permittivity satisfactorily.

Wet snow

From Equations (9) and (10) the excess permittivity of wet snow due to the liquid water follows:

(16)

(17)

This is the difference between the permittivities of wet snow and the corresponding dry snow (that snow which is left when all liquid water is replaced by air).

Different values for the parameter a give at 1 GHz and 0°C:

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

The graphs of these formulae are shown in Figures 1–4. The empirical curves at 1 GHz have the form

(26)

(27)

based on experimental resultsReference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen (Tiuri and others, 1984), are also shown.

Fig. 1. The increase in the real part of the permittivity of snow due to liquid water according to exponential models. The broken line is empiricalReference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen (Tiuri and others, 1984).

Fig. 2. The increase in the real part of the permittivity of snow due to liquid water (exponential models).

Fig. 3. The increase in the imaginary part of the permittivity of snow due to liquid water (exponential models). The broken line is empirical Reference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen(Tiuri and others, 1984).

Fig. 4. The increase in the imaginary part of the permittivity of snow due to liquid water (exponential models).

Structure-dependent models

Different dielectric mixing models will be presented that take into account the microscopic structure of the mixture. Ice and water are considered as the inclusion phases, the host material being air. The models take into account the shape of the inclusion particles. The mixing theories have been reported by Reference TaylorTaylor (1965), Reference Tinga, Tinga, Voss and BlosseyTinga and others (1973), and Reference Polder and SantenPolder and van Santen (1946).

Taylor

The theory of Taylor leads to different formulae depending on the shape of the inclusions. For randomly oriented needles the formula is

(28)

where .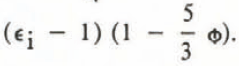

For randomly oriented disc-shaped inclusions the complex permittivity is

(29)

For spherical inclusions the mixing formula is

(30)

Where b = ϵ_i − 2 + 3ϕ − 3ϕϵ_i. This formula has also been derived by Reference BöttcherBöttcher (1952). Essentially the same results are obtained from the theory of Polder and van Santen.

For randomly oriented inclusions that are not discs, needles, or spheres but ellipsoids with known semi-axes the mixing formula is

(31)

where N ₁, N ₂, and N ₃ are the depolarization factors of the ellipsoids with semi-axes (a ₁, a ₂, a ₃):

(32)

The equation

(33)

also holds. If two semi-axes of the ellipsoids are equal, two of the depolarization factors are also equal

(34)

for prolate ellipsoids, and

(35)

for oblate ellipsoids. The ellipticity e is the ratio of the smaller semi-axis to the greater one. For ellipsoids of revolution in general the following mixing formula is valid:

(36)

where N = N ₁ = N ₂, the depolarization factor of the ellipsoid in the direction of the two equal semi-axes. For discs N = 0, for spheres N = 1/3, for needles N = 1/2, for prolate ellipsoids 1/3 ⩽ N ⩽ 1/2, and for oblate ellipsoids 0 ⩽ N ⩽ 1/3.

Dry snow

Formulae (28), (29), and (30) give the complex dielectric constant of dry snow. For randomly oriented needle-shaped ice inclusions

(37)

(38)

For randomly oriented disc-shaped ice inclusions

(39)

(40)

For spherical ice inclusions

(41)

(42)

The dielectric constant of ice is assumed to be ϵ_ice = 3.15 − jϵ″_ice and the assumption ϵ″_ice << e′_ice is made. The volume part of ice is ϕ = ρ_s/ρ_ice. ρ_s is ρ_ice = 0.917 Mg/m³. In Figures 5 and 6 the results are illustrated together with the empirical results by Reference NyforsNyfors (1982).

Fig. 5. The real part of the dielectric constant of dry snow according to structure-dependent models. The points are experimental from Reference NyforsNyfors (1982).

Fig. 6. The loss tangent of dry snow according to structure-dependent models. The experimental points are from Reference NyforsNyfors (1982). The experimental points contain five sets of measurements. The data are relative to the densest sample in each set, which has been forced to fit the curve for needles.

Taylor, needles

(43)

(44)

Taylor, discs

(45)

(46)

Taylor, spheres

(47)

(48)

These formulae are depicted in Figures 7–10 together with the experimental resultsReference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen Tiuri and others, (1984).

Fig. 7. The increase in the real part of the permittivity of snow due to liquid water according to structure-dependent models. N – Taylor, needles; D – Taylor, discs; S – Taylor, spheres, TINGA – Tinga and others, spheres. The broken line is empirical Reference Tiuri, Tiuri, Sihvola, Nyfors and HallikainenTiuri and others, (1984).

Fig. 8. The increase in the real part of the permittivity of snow due to liquid water (structure-dependent models). N – Taylor, needles; D – Taylor, discs; S – Taylor, spheres; TINGA – Tinga and others, spheres.

Fig. 9. (The increase in) the imaginary part of the permittivity of snow due to liquid water (structure-dependent models). N – Taylor, needles; D – Taylor, discs; S – Taylor, spheres; TINGA – Tinga and others, spheres. The broken line is empirical Reference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen(Tiuri and others, 1984).

Fig. 10. The increase in the imaginary part of the permittivity of snow due to liquid water (structure-dependent models). N – Taylor, needles; D – Taylor, discs; S – Taylor, spheres: TINGA – Tinga and others, spheres.

Taylor, prolate and oblate ellipsoids

∆ϵ_s′ and ϵ_s″ can be numerically solved from the complex Equation (36) by substituting ϵ_m = ∆ϵ_s′ + 1 − jϵ_s″ and ϵ_w = 88.0 − j9.79. The results for differently shaped ellipsoids are given in Figures 11–14 with the experimental resultsReference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen Tiuri and others, (1984).

Fig. 11. The increase in the real part of the permittivity of snow due to liquid water. Taylor model, prolate ellipsoids. The parameter N is the depolarization factor of the ellipsoids in the direction of the shorter semi-axes.

Fig. 12. The increase in the real part of the permittivity of snow due to liquid water. Taylor model, oblate ellipsoids. The parameter N is the depolarization factor of the ellipsoids in the direction of the longer semi-axes.

Fig. 13. (The increase in) the imaginary part of the Taylor model, prolate ellipsoids. The parameter N is the depolarization factor of the ellipsoids in the direction of the shorter semi-axes.

Fig. 14. (The increase in) the imaginary part of the Taylor model, oblate ellipsoids. The parameter N is the depolarization factor of the ellipsoids in the direction of the longer semi-axes.

Tinga and others

The theory of Reference Tinga, Tinga, Voss and BlosseyTinga and others (1973) yields for spheres

(49)

For dry snow (ice–air mixture) assuming that ϵ_ice = 3.15 − jϵ″_ice and ϵ″ << ϵ′_ice

(50)

(51)

These functions are given in Figures 5 and 6

The excess permittivity of wet snow due to liquid water at 1 GHz and 0°C is

(52)

(53)

These formulae are depicted in Figures 7–10 together with the experimental resultsReference Tiuri, Tiuri, Sihvola, Nyfors and Hallikainen (Tiuri and others, 1984).

Chaloupka’s y-function

Chaloupka, Ostwald, and Schiek have studied the dielectric properties of wet materials and the effect of the geometrical shape of the water particles (Reference Chaloupka, Chaloupka, Ostwald and SchiekChaloupka and others, 1980; Reference Ostwald, Ostwald, Schiek and ChaloupkaOstwald and others, 1980). They apply the mixing formula of Polder and van Santen for which they need to know the distribution function of the water inclusions. They calculate this function via the measurable real and imaginary parts of the dielectric constant of the mixture. They define the quotient Y as

(54)

where ϵ_dry is the permittivity of the dry material, and ϵ_m′ − jϵ_m″ the complex permittivity of the mixture of this dry material and water.

The central feature in this Y-function from the point of view of tentative mixing theories, is the assertion stated by Chaloupka, Ostwald, and Schiek that the Y-function is independent of the water content. In other words, any amount of liquid water augments in the same rate both the real and imaginary part of the material. Applied to the air–water mixture discussed in this paper, the Y-function will be

(55)

Therefore the flatness of a plot of the y-function versus water volume W is a measure of the pertinence of the Chaloupka approach to a water-mixture model.

If the y-function is flat for a mixing model, then its reciprocal 1/Y will also be flat. It seems more natural to compare the change in the imaginary part to the change in the real part due to liquid water, i.e. to calculate the function 1/Y = ϵ_S″/∆ϵ_s′. Experimental results (26) and (27) give support to the thesis of Chaloupka and others, namely that 1/Y = tan δ_w. Figures 15 and 16 show the behaviour of the y-function according to mixing models discussed in this paper.

Fig. 15. The 1/Y-function Reference Chaloupka, Chaloupka, Ostwald and Schiek(Chaloupka and others, 1980) of exponential models.

Fig. 16. The 1/Y-function Reference Chaloupka, Chaloupka, Ostwald and Schiek(Chaloupka and others, 1980) of structure-dependent models.

Discussion

Figures 1–4 show that the parameter a in exponential models should be near 1/3 for the real part of the dielectric constant and near 1/2 for the imaginary part of the dielectric constant in order to explain the dielectric behaviour of the liquid water in snow. Both parameter values give also good results in explaining the permittivity of dry snow (Equations (9)–(13)).

From Figures 5 and 6 it can be seen that the mixing theory of Taylor with randomly oriented disc-shaped ice inclusions agrees with experimental results for the permittivity of snow. For very light new snow the mixture theory with random orientation of needles gives better values and for very dense snow spherical particles give the best results. The mixture theory of Tinga and others with spherical inclusions gives values that are too low. In the range ρ_s < 0.5 Mg/m³ the linear function ϵ_s′ = 1 + 2ρ_s is a tolerable rule of thumb.

For the disc, needle, and sphere models explaining the air–water mixture (Figs 7–10) the situation seems worse than for the exponential models: the needle and disc models of Taylor predict too large values and the sphere models of both Taylor and Tinga and others too small values for both the real and imaginary parts of the dielectric constant of the mixture. In particular the model of Tinga and others is extremely inconsistent with experimental results.

From Figures 11–14 it can be seen that both prolate and oblate ellipsoids are able to explain the experimental results of the real part of the excess permittivity due to liquid water. For the real part of the permittivity of the mixture, the depolarization factors N = 0.48 for prolate ellipsoids and N = 0.08 for oblate ellipsoids give the correct dielectric behaviour. This means that the water inclusions have ellipticity (axial ratio) e = 0.16 (prolate case) or e = 0.12 (oblate case). The results for the imaginary part show that the experimental behaviour in the wetness range W = 0–10% by volume does not have the same curvature as the mixing models but the prolate ellipsoid assumption is more consistent with it. Also the corresponding depolarization factor (0.49) is near to the depolarization factor of the real part (0.48). However, the figures for the real part of the permittivity should be stressed more, because the accuracy in the measurements of the real part, on which the empirical curve is based, is greater than the accuracy of the experimental curve for the imaginary part.

One possibility that increases the degree of freedom in the model is to assume a distribution function for the axial ratio of the water inclusions. Nevertheless, the theoretical treatment will become tedious, and the formulae resulting from the exponential models may be more suitable for engineering applications.

Finally, Figures 15–16 show that in Chaloupka’s sense the exponential models are the better the nearer the parameter a is to unity. From the structure-dependent models, the needle and disc models of Taylor are very good, but the sphere models of Taylor and especially Tinga and others are extremely poor.