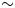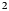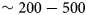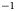1. Introduction
The magnitude, and timing, of the Antarctic Ice Sheet (AIS)'s contribution to sea level rise is still difficult to predict in large part due to the need of better understanding surface mass balance (SMB) and its future evolution (Fox-Kemper and others, Reference Fox-Kemper and Masson-Delmotte2021). SMB is the net addition or removal of mass at the surface of the ice sheet. For the AIS, SMB is dominated by snow accumulation (Van Wessem and others, Reference Van Wessem2018; Agosta and others, Reference Agosta2019), while the main sinks are sublimation, wind-driven ablation and wind-driven sublimation (with surface melting negligible across the majority of the ice sheet, Lenaerts and others, Reference Lenaerts, Medley, van den Broeke and Wouters2019; Medley and others, Reference Medley, Neumann, Zwally and Smith2020). A recent study showed that between 1994 and 2017, the AIS lost 2.5 trillion tonnes of ice, the majority driven by oceanic melting (both direct and indirect effects, Slater and others, Reference Slater2021). However, the projected increasing atmospheric near-surface temperatures could lead to higher snowfall, and thus more positive SMB, due to an increase in the saturation vapor pressure of the air, following the Clausius–Clapeyron relationship (Frieler and others, Reference Frieler2015; Fudge and others, Reference Fudge2016; Dalaiden and others, Reference Dalaiden2020).
To document and understand SMB past and future changes, there are three complementary sources of information that can be examined. Firstly, we have in situ measurements, which provide the best observational constraints of SMB. Snow stakes, snow pits and firn/shallow ice cores (up to a few hundred meters) provide a SMB record with a high temporal resolution (seasonal, annual or multi-annual) as snow deposited at the surface has not undergone any significant vertical deformation and the annual layers are relatively thick, depending on the surface accumulation rate. In practice, SMB in ice cores is obtained from the measurement of the thickness of firn or ice that has accumulated between dated markers within the core after taking into account the effect of densification, compaction and ice flow. Shallow ice cores are often dated by annual layer counting near the surface and isotope measurements, refined by chemistry and electrical conductivity measurements (e.g. Philippe and others, Reference Philippe2016). Deeper ice cores, i.e. cores that extend beyond a couple hundred meters, provide longer term SMB constraints but at a lower temporal resolution due to the increasing impact of vertical strain with depth such that annual depositional layers cannot be resolved anymore. Ice cores are impacted by measurement errors due to depth, density and age uncertainties (Parrenin and others, Reference Parrenin2012; Rupper and others, Reference Rupper2015), which affect their SMB record as a result. The ice core SMB record can also be strongly modified by post-depositional reworking of the surface by winds that can erode away snow in one location and redeposit it several kilometers away or remove it completely through wind-driven sublimation (King and others, Reference King2004; Lenaerts and others, Reference Lenaerts, Medley, van den Broeke and Wouters2019; Agosta and others, Reference Agosta2019). SMB can be highly variable, even over the distance of a few meters (Gautier and others, Reference Gautier, Savarino, Erbland, Lanciki and Possenti2016; Kausch and others, Reference Kausch2020; Münch and others, Reference Münch, Werner and Laepple2021), and post-depositional reworking can further modify this spatial SMB variability (Zuhr and others, Reference Zuhr, Münch, Steen-Larsen, Hörhold and Laepple2021). With a surface area of $\sim 50$![]() cm$^{2}$
cm$^{2}$![]() , ice cores therefore have the potential to capture a local and noisy record of past SMB conditions. Averaging ice core records in proximity together can increase the signal to noise ratio of their records, but the current ice core network density is insufficient to increase this ratio significantly (Cavitte and others, Reference Cavitte, Dalaiden, Goosse, Lenaerts and Thomas2020; Casado and others, Reference Casado, Münch and Laepple2020).
, ice cores therefore have the potential to capture a local and noisy record of past SMB conditions. Averaging ice core records in proximity together can increase the signal to noise ratio of their records, but the current ice core network density is insufficient to increase this ratio significantly (Cavitte and others, Reference Cavitte, Dalaiden, Goosse, Lenaerts and Thomas2020; Casado and others, Reference Casado, Münch and Laepple2020).
Secondly, regional climate models (RCMs), especially polar-focused models such as RACMO (Lenaerts and others, Reference Lenaerts2012; Noël and others, Reference Noël2015; Van Wessem and others, Reference Van Wessem2018) and MAR (Agosta and others, Reference Agosta2019), forced by re-analysis climate data, provide SMB constraints over the whole AIS. They provide these SMB constraints at a much higher temporal resolution than ice cores, often up to a 6-hourly resolution, for the entire time period since 1979. However, these models are also impacted by uncertainties: by their inherent construction, they might not represent the reality well enough due to missing important dynamic processes. With a grid resolution of $\sim 5$![]() km at best, their spatial resolution is still too coarse to resolve some processes that are active and recorded in the observations (e.g. wind-driven erosion, Agosta and others, Reference Agosta2019; Dattler and others, Reference Dattler, Lenaerts and Medley2019). Ice core measurements and models often disagree, with ice cores showing a much larger variability in SMB than models (Medley and Thomas, Reference Medley and Thomas2019), while for a same region, modeled and observed SMB trends can be very different (Goursaud and others, Reference Goursaud2017).
km at best, their spatial resolution is still too coarse to resolve some processes that are active and recorded in the observations (e.g. wind-driven erosion, Agosta and others, Reference Agosta2019; Dattler and others, Reference Dattler, Lenaerts and Medley2019). Ice core measurements and models often disagree, with ice cores showing a much larger variability in SMB than models (Medley and Thomas, Reference Medley and Thomas2019), while for a same region, modeled and observed SMB trends can be very different (Goursaud and others, Reference Goursaud2017).
Finally, ice-penetrating radar data provide a SMB record at a high spatial resolution (in the order of meters along a radar transect, in the order of kilometers across track depending on the radar survey design). It therefore has the potential to fill the spatial gap between the very local ice core records and the models with a coarser grid size. Internal reflecting horizons (IRHs), visible in the radar data between the surface and the bedrock below, can originate from three different processes: density changes near the surface in the firn column, variations in the acidity content of the ice throughout the ice column, and at depth from the alignment of crystal fabrics in the ice (Fujita and Mae, Reference Fujita and Mae1994; Eisen and others, Reference Eisen2008). In the case of density changes or acidity concentration variations, the induced IRHs are considered to have isochronal properties, i.e. all connected points along an IRH have the same age. Depending on their brightness, continuity and the radar survey design (Cavitte and others, Reference Cavitte2016), they can be traced over very large distances across the ice sheet. Where they intersect an ice core site, their depths and that of the ice core can be matched to obtain a dated internal stratigraphy (Eisen and others, Reference Eisen2008; Cavitte and others, Reference Cavitte2016; Winter and others, Reference Winter2017). The depth and age of successive IRHs can then be used to calculate the SMB for each time interval between a pair of IRHs, corrected for snow density (Medley and others, Reference Medley2013; Kausch and others, Reference Kausch2020). The vertical resolution of the radar system used will determine the temporal resolution of the SMB record that can be reconstructed from the radar data. Although radar-derived SMB records are dependent upon ice core records for absolute SMB rates, they provide interesting information on the spatial variability of the SMB. Combined with ice core measurements, radar data can be informative about the representativeness of a pointwise measurement of a larger surface area.
In this work, we set out to quantify the spatial representativeness of a single ice core's SMB record using co-located ice core and ice-penetrating radar records for three ice rises in East Antarctica. The radar surveys provide a SMB record over an area of a few square kilometers and cover the past six or seven decades. These radar-derived SMB records allow us to evaluate the spatial representativeness of the ice core SMB record in terms of mean state, as well as multi-annual to decadal variability, of the SMB signal, over those decennial timescales. Both the mean signal and the temporal variability are highly relevant in data-model comparisons, where RCM SMB simulations are assessed using pointwise in situ measurements of SMB. Mean SMB is relevant in the assessment of the model ability to reproduce regional variations, while temporal variability of the SMB signal is relevant typically for identifying trends and the contribution of modes of atmospheric variability.
2. Study area
We focus our study on three consecutive ice rises located along the Princess Ragnhild Coast, East Antarctica (Fig. 1). These three ice rises have the advantages of (1) having co-located ice core and shallow radar data and (2) of being supposedly affected by the same climate. The eastern-most ice rise is the Derwael Ice Rise (DIR), an isolated ice rise in the middle of the Roi Baudouin ice shelf at 26.4$^{\circ }$![]() E. It is a relatively thick dome-shaped ice rise reaching a height of $\sim 429$
E. It is a relatively thick dome-shaped ice rise reaching a height of $\sim 429$![]() m above sea level, with a maximum ice thickness of $\sim 550$
m above sea level, with a maximum ice thickness of $\sim 550$![]() m (Drews and others, Reference Drews2015; Philippe and others, Reference Philippe2016). DIR is $\sim 31$
m (Drews and others, Reference Drews2015; Philippe and others, Reference Philippe2016). DIR is $\sim 31$![]() km wide east-west by $\sim 40$
km wide east-west by $\sim 40$![]() km long north-south at its topographic maximum (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). At 55 km to the west of DIR is the Lokeryggen Ice Rise (LIR), located on the western edge of the Roi Baudouin ice shelf at 24.0$^{\circ }$
km long north-south at its topographic maximum (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). At 55 km to the west of DIR is the Lokeryggen Ice Rise (LIR), located on the western edge of the Roi Baudouin ice shelf at 24.0$^{\circ }$![]() E. Geomorphologically, LIR is a promontory, as it is attached to the main land through a topographic saddle. LIR reaches $\sim 333$
E. Geomorphologically, LIR is a promontory, as it is attached to the main land through a topographic saddle. LIR reaches $\sim 333$![]() m above sea level with an ice thickness of $\sim 420$
m above sea level with an ice thickness of $\sim 420$![]() m and is $\sim 57$
m and is $\sim 57$![]() km wide east-west at its topographic maximum (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Finally, Hammarryggen Ice Rise (HIR) is located 40 km the west of LIR, at 21.8$^{\circ }$
km wide east-west at its topographic maximum (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Finally, Hammarryggen Ice Rise (HIR) is located 40 km the west of LIR, at 21.8$^{\circ }$![]() E, and separates the Muninisen and the Jotneisen ice shelves. HIR is also a promontory, reaching a maximum height of $\sim 348$
E, and separates the Muninisen and the Jotneisen ice shelves. HIR is also a promontory, reaching a maximum height of $\sim 348$![]() m above sea level with an ice thickness of $\sim 550$
m above sea level with an ice thickness of $\sim 550$![]() m, and is separated from the main land by a topographic saddle (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Its geometry is somewhat more unusual with a triangular shape ($\sim 48$
m, and is separated from the main land by a topographic saddle (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Its geometry is somewhat more unusual with a triangular shape ($\sim 48$![]() km equilateral sides) and a triple junction ice divide; a precise ice thickness is not known due to the lack of deep radar constraints.
km equilateral sides) and a triple junction ice divide; a precise ice thickness is not known due to the lack of deep radar constraints.

Fig. 1. The Princess Ragnhild Coast with the three ice rises examined, from west to east: Hammarryggen Ice Rise, Lokeryggen Ice Rise and Derwael Ice rise. The ground-penetrating radar surveys are shown as black lines, the ice core sites are indicated by red pins. For context, the Reference Elevation Model of Antarctica (REMA) is shown (units are meters and are referenced to the WGS84 ellipsoid, 8 m horizontal resolution product) with thin black 50 m elevation contours, green colors indicate the ice shelves and light blue colors indicate the open ocean. A thin dashed blue line locates the MEASURES grounding line (Rignot and others, Reference Rignot, Jacobs, Mouginot and Scheuchl2013; Mouginot and others, Reference Mouginot, Rignot and Scheuchl2017). The inset locates the study area. Projection is Polar Stereographic ps71, vertical exaggeration 40x. This figure was prepared with Quantarctica (Matsuoka and others, Reference Matsuoka2021).
The climate along the Princess Ragnhild Coast is characterized by sporadic marine air intrusions mostly from the northeast that bring moist warm air inland (Gorodetskaya and others, Reference Gorodetskaya2013; Lenaerts and others, Reference Lenaerts2014). As this air is forced up over the topographic high created by the ice rises, most of the moisture is lost through snowfall on the windward side, resulting in a dryer leeward side due to adiabatic warming of the air flowing down-slope. In addition, katabatic winds are active along the coast, usually flowing down the Antarctic Plateau from the southeast due to the influence of the Coriolis effect on the south-to-north katabatic flows. The combination of the marine air intrusions and the katabatic winds brings winds that are predominantly from the east along the Princess Ragnhild Coast. These can result in significant surface erosion and re-deposition of the surface snow layers (King and others, Reference King2004; Matsuoka and others, Reference Matsuoka2015; Lenaerts and others, Reference Lenaerts, Medley, van den Broeke and Wouters2019; Kausch and others, Reference Kausch2020), which alters the SMB pattern over ice rises.
3. Methods
3.1. Data sets
3.1.1. Radar data sets
Each ice rise was surveyed with the ground-penetrating GSSI TerraSIRch SIR System-3000 radar which is a lightweight, portable, single-channel radar system pulled behind a ski-doo. The GPR data were collected at a 400 MHz center frequency and the vertical number of samples is chosen such that it images the upper 50 m of the snow/ice column at a high vertical resolution, providing annual to multi-annual temporal resolution (Drews and others, Reference Drews2015; Callens and others, Reference Callens, Drews, Witrant, Philippe and Pattyn2016; Kausch and others, Reference Kausch2020). The GPR radar data were collected in December 2012 at DIR, in December 2017 at LIR and in December 2018 at HIR. No pre-processing of the radar data was applied. Post-processing consists of applying a simple gain function (for the DIR GPR data), a bandpass filter (50–900 MHz at DIR, and 200–600 MHz at LIR and HIR), removing the background noise and applying a dewow filter (at LIR and HIR). The radar data were geolocated using GNSS receivers which were time-synchronized to the GSSI radar. We collected a kinematic GPS survey using Trimble L1/L2 receivers with one rover receiver installed on the ski-doo and one stationary receiver located at camp. The coordinates of the stationary receiver were determined from the mean of its position over several hours of data collection. The rover receiver positions were then post processed differentially (L1/L2 combined) with respect to the stationary receiver, using RTKLIB, an open source program package for GNSS positioning. As the rover receiver is positioned on a moving ski-doo, we estimate this introduces a positioning error of $\sim 20$![]() cm (given a maximum ski-doo speed of 8 km h$^{-1}$
cm (given a maximum ski-doo speed of 8 km h$^{-1}$![]() ). Adding in the absolute error of the stationary receiver, the positions calculated are accurate to within 1–2 m.
). Adding in the absolute error of the stationary receiver, the positions calculated are accurate to within 1–2 m.
3.1.2. Ice core data sets
An ice core record has been recovered at the crest of each ice rise. At DIR, the 120 m-long ice core was drilled in December 2012 (IC12), and is located 429 m above sea level at $-70.24218^{\circ }$![]() S, 26.34162$^{\circ }$
S, 26.34162$^{\circ }$![]() E. The mean length of each ice core section recovered per run was 77 cm, with a standard deviation of 40 cm (Philippe and others, Reference Philippe2016). Annual layer counting, using the stable water isotopes $\delta ^{18}$
E. The mean length of each ice core section recovered per run was 77 cm, with a standard deviation of 40 cm (Philippe and others, Reference Philippe2016). Annual layer counting, using the stable water isotopes $\delta ^{18}$![]() O and $\delta$
O and $\delta$![]() D, electrical conductivity (ECM) measurements and major ions measurements were used to date the ice core, providing a youngest and oldest age-depth chronology (Philippe and others, Reference Philippe2016). Combined with a depth-density profile measured by direct gravimetric weighing of the ice core sections (Hubbard and others, Reference Hubbard2013) and with two vertical strain rates models, the more probable oldest chronology (in accordance with the occurrence of the Tambora eruption) provided annual SMB estimates in m w.e a$^{-1}$
D, electrical conductivity (ECM) measurements and major ions measurements were used to date the ice core, providing a youngest and oldest age-depth chronology (Philippe and others, Reference Philippe2016). Combined with a depth-density profile measured by direct gravimetric weighing of the ice core sections (Hubbard and others, Reference Hubbard2013) and with two vertical strain rates models, the more probable oldest chronology (in accordance with the occurrence of the Tambora eruption) provided annual SMB estimates in m w.e a$^{-1}$![]() . At LIR, the 208 m-long ice core (FK17, S. Wauthy, pers. comm., 2022) was drilled during the 2017/2018 austral summer ($-70.53648^{\circ }$
. At LIR, the 208 m-long ice core (FK17, S. Wauthy, pers. comm., 2022) was drilled during the 2017/2018 austral summer ($-70.53648^{\circ }$![]() S, 24.07036$^{\circ }$
S, 24.07036$^{\circ }$![]() E), using the intermediate-depth ECLIPSE ice core drill. As the drill was set-up in a $\sim 2$
E), using the intermediate-depth ECLIPSE ice core drill. As the drill was set-up in a $\sim 2$![]() m deep trench, a short $\sim 9$
m deep trench, a short $\sim 9$![]() m core (FK18) was recovered in the following season (austral 2018/2019) to obtain a complete age-depth chronology. The cores were cut in 50 cm sections prior to analysis and transport, and were processed at the Université libre de Bruxelles. An age-depth chronology has been obtained by annual layer counting using the stable water isotopes, and refined using ice chemistry, ECM measurements and volcanic eruptions matching. In addition, a density-depth profile was measured for the top 125 m of the ice core by triple weighting the previously cut ice core sections ($\sim 3\times 50$
m core (FK18) was recovered in the following season (austral 2018/2019) to obtain a complete age-depth chronology. The cores were cut in 50 cm sections prior to analysis and transport, and were processed at the Université libre de Bruxelles. An age-depth chronology has been obtained by annual layer counting using the stable water isotopes, and refined using ice chemistry, ECM measurements and volcanic eruptions matching. In addition, a density-depth profile was measured for the top 125 m of the ice core by triple weighting the previously cut ice core sections ($\sim 3\times 50$![]() cm sticks). At HIR, the 262 m-long ice core (T18, Wauthy et al., in prep.), was drilled in the 2018/2019 austral summer ($-70.49960^{\circ }$
cm sticks). At HIR, the 262 m-long ice core (T18, Wauthy et al., in prep.), was drilled in the 2018/2019 austral summer ($-70.49960^{\circ }$![]() S, 21.88017$^{\circ }$
S, 21.88017$^{\circ }$![]() E), using the intermediate-depth ECLIPSE ice core drill. As the drill was set-up in a 2.40 m deep trench, a short 10 m core (T18-shallow) was drilled nearby to obtain a complete chronology. The cores were cut in 50 cm sections and were processed at the Université libre de Bruxelles, as for FK17. A complete depth-density profile was obtained by triple weighting the recovered 50 cm cores directly in the field. The age-depth chronology has been obtained following the same steps as for FK17: annual layer counting using the stable water isotopes with refinement using ice chemistry, ECM measurements and volcanic eruptions matching.
E), using the intermediate-depth ECLIPSE ice core drill. As the drill was set-up in a 2.40 m deep trench, a short 10 m core (T18-shallow) was drilled nearby to obtain a complete chronology. The cores were cut in 50 cm sections and were processed at the Université libre de Bruxelles, as for FK17. A complete depth-density profile was obtained by triple weighting the recovered 50 cm cores directly in the field. The age-depth chronology has been obtained following the same steps as for FK17: annual layer counting using the stable water isotopes with refinement using ice chemistry, ECM measurements and volcanic eruptions matching.
3.2. Obtaining a dated internal radar stratigraphy
We use the OpendTect open-source software to trace the internal stratigraphy at each ice rise. At each ice rise, we trace as many IRHs as possible in the vertical – to maximize temporal resolution – and as spatially extensive as achievable from the radar data, in order to compare it to the ice core records. We choose them on the basis of their bright return and their lateral continuity. Any IRH that cannot be traced on a majority of the transects of the ice rise's radar survey is discarded. Each radar survey is designed to have a number of crossovers, which are used to ensure that each IRH is traced consistently across the whole radar survey. This is done by visually matching the IRHs’ depths across intersecting transects. In total, six IRHs are traced across the DIR and HIR radar surveys and seven across the LIR survey, evenly distributed across the top 50 m of the ice column (supplementary Figs S1–S3). IRHs are traced on the radargrams in two-way-travel-time (TWTT).
To assign ages to the traced IRHs, we first convert from TWTT to depth (Table 1) in order to match the IRH depths to the ice core depths. We use the depth-density profiles measured at each ice core site (see section Data sets) and the Kovacs function (Kovacs and others, Reference Kovacs, Gow and Morey1995) that determines the permittivity of the firn $\epsilon$![]() based on its density $\rho$
based on its density $\rho$![]() following:
following:
with $\rho$![]() in g cm$^{-3}$
in g cm$^{-3}$![]() . Note that because the raw density measurements are noisy (supplementary Fig. S4), we use an exponential fit of the ice cores’ depth-density profiles (as defined at DIR, Hubbard and others, Reference Hubbard2013) with parameters adapted for each ice core site to obtain the best r $^{2}$
. Note that because the raw density measurements are noisy (supplementary Fig. S4), we use an exponential fit of the ice cores’ depth-density profiles (as defined at DIR, Hubbard and others, Reference Hubbard2013) with parameters adapted for each ice core site to obtain the best r $^{2}$![]() fit between the raw measurements and the exponential fit (orange line in Fig. S4). Depth $z$
fit between the raw measurements and the exponential fit (orange line in Fig. S4). Depth $z$![]() can then be obtained from permittivity following:
can then be obtained from permittivity following:
where $C_{{\rm air}}$![]() is the electromagnetic wave speed in air.
is the electromagnetic wave speed in air.
Table 1. Depths and ages of the IRHs at each ice rise

IRH, internal reflecting horizon; DIR, Derwael ice rise; LIR, Lokeryggen ice rise; HIR, Hammarryggen ice rise.
$^{{\rm a}}$![]() Depths are measured at the point of closest approach to the ice core site, or in the case of DIR, as the average depth over the three closest locations to the ice core site.
Depths are measured at the point of closest approach to the ice core site, or in the case of DIR, as the average depth over the three closest locations to the ice core site.
The internal stratigraphy is dated using the co-located ice core within each radar survey. In the case of LIR and HIR, each IRH is dated at the point of its closest approach to the ice core site in the radar survey, i.e. 16–26 m away for LIR and 27–42 m away for HIR. We assume horizontal continuity over those distances. The IRH depths can then be matched to the ice core depths and assigned the corresponding ice core ages. At these two ice rises, the IRHs traced span the past seven decades (Table 1). In the case of DIR, because the point of closest approach is 485 m away from the ice core site and the IRHs dip strongly over this distance, we cannot assume horizontal continuity. Since the ice core was retrieved at the top of the ice rise divide, which is aligned with a Raymond arch crest under the ice surface (Raymond, Reference Raymond1983; Drews and others, Reference Drews2015), we measure the IRH depths at the three closest locations to the ice core site where the radar survey intersects the Raymond arch (524, 1494 and 1905 m away). Assuming that the depth of the IRHs at these three sites matches their depth at the ice core site, we can assign the corresponding ice core age for each location. We then calculate the mean depth and mean age across all three locations that we assign as the IRHs’ best guess of depth and age at the DIR ice core site. This induces a larger age uncertainty for the DIR SMB record, which we keep in mind during our discussion. The IRHs traced over DIR cover the past five decades.
3.3. Calculating radar SMB rates from the dated internal stratigraphy
Using the dated internal stratigraphy, we can calculate the SMB history over the past five to seven decades across each ice rise, i.e. the SMB between each pair of consecutive IRHs in depth (as in MacGregor and others, Reference MacGregor2015; Dattler and others, Reference Dattler, Lenaerts and Medley2019). Because the IRHs studied here are within the firn layer, density varies with depth. In addition, snow density shows significant spatial variability at ice rises in general. Analysis of 3 m firn cores at three ice rises across the Fimbul ice shelf shows a 35% snow density spatial variation between the ice rises (Matsuoka and others, Reference Matsuoka2015), while local snow micropen measurements collected recently over the three ice rises show a high variation in density spatially in the first meter (N. Wever, pers. comm., 2022). The measured depth-density profiles can only be used at the location closest to the ice core site. For all other points along the radar transects, we use the Herron–Langway (HL) firn densification profile (Herron and Langway, Reference Herron and Langway1980) to find the best-fit depth-density profile.
This best-fit depth-density profile is obtained by iterating over the calculated mean SMB history (SMB calculated between the surface and a given IRH, Eq. 4) from the HL model until the mean SMB values converge between two successive iterations. Those iterations are required as the SMB influences the density profile, which itself is constrained by the SMB. We use a surface density of 0.434 g cm$^{-3}$![]() (mean surface density over all three ice core sites), a surface air temperature of –16$^{\circ }$
(mean surface density over all three ice core sites), a surface air temperature of –16$^{\circ }$![]() C (mean value for the ice rises according to the RACMO2.3 5.5 km simulations over 1979–2017, Lenaerts and others (Reference Lenaerts2017)), and a reasonable initial first guess for the region for the mean SMB between the surface and each IRH was set at 50 cm w.e. a$^{-1}$
C (mean value for the ice rises according to the RACMO2.3 5.5 km simulations over 1979–2017, Lenaerts and others (Reference Lenaerts2017)), and a reasonable initial first guess for the region for the mean SMB between the surface and each IRH was set at 50 cm w.e. a$^{-1}$![]() for all IRHs. From this, the HL model is used to calculate an initial depth-density relationship. This initial depth-density profile is then used to obtain the resulting mean SMB. Those SMB values are fed back simultaneously into the HL model, to calculate a new depth-density profile and new mean SMB values. The latest mean SMB values are compared to the mean SMB values obtained in the previous iteration. We repeat this process until mean SMB values between two iterations are within 0.5 cm w.e. a$^{-1}$
for all IRHs. From this, the HL model is used to calculate an initial depth-density relationship. This initial depth-density profile is then used to obtain the resulting mean SMB. Those SMB values are fed back simultaneously into the HL model, to calculate a new depth-density profile and new mean SMB values. The latest mean SMB values are compared to the mean SMB values obtained in the previous iteration. We repeat this process until mean SMB values between two iterations are within 0.5 cm w.e. a$^{-1}$![]() of each other for all IRH depths (which usually takes max 3 iterations). We use an ice density of 0.917 g cm$^{-3}$
of each other for all IRH depths (which usually takes max 3 iterations). We use an ice density of 0.917 g cm$^{-3}$![]() and calculate the HL density-depth profile at a vertical resolution of 1 cm.
and calculate the HL density-depth profile at a vertical resolution of 1 cm.
Using a 1 cm $\Delta z_i$![]() increment, Eqns 1 and 2 and the HL depth-density profile obtained, we define the cumulative mass CM$_k$
increment, Eqns 1 and 2 and the HL depth-density profile obtained, we define the cumulative mass CM$_k$![]() (expressed in m w.e) from the surface and a given depth $z_i = k \Delta z_i$
(expressed in m w.e) from the surface and a given depth $z_i = k \Delta z_i$![]() as:
as:
with $\overline {\rho _i}$![]() the mean density of the depth increment $\Delta z_i$
the mean density of the depth increment $\Delta z_i$![]() .
.
We then define the cumulative mass CM$_{{\rm IRH}_n}$![]() above a given IRH$_n$
above a given IRH$_n$![]() (expressed in m w.e.) as the sum over $i = 0$
(expressed in m w.e.) as the sum over $i = 0$![]() to $i = k$
to $i = k$![]() with $k$
with $k$![]() such that $\sum _{i = 0}^{k} \Delta z_i = z_{{\rm IRH}_n}$
such that $\sum _{i = 0}^{k} \Delta z_i = z_{{\rm IRH}_n}$![]() where $z_{{\rm IRH}_n}$
where $z_{{\rm IRH}_n}$![]() is the depth to a given IRH.
is the depth to a given IRH.
The mean SMB (between the surface and a given IRH$_n$![]() ), at every point along the radar transect, is then given by:
), at every point along the radar transect, is then given by:
While the SMB between two successive isochrones IRH$_n$![]() and IRH$_{n + 1}$
and IRH$_{n + 1}$![]() , with ages age$_n$
, with ages age$_n$![]() and age$_{n + 1}$
and age$_{n + 1}$![]() , is calculated as:
, is calculated as:
We bring to attention that we do not apply a vertical strain rate model to calculate SMB, so the radar-derived SMB record is not corrected for the vertical strain rate. To compare our radar-derived uncorrected SMB record to the measured SMB from the ice core, we also use the uncorrected ice core SMB values, i.e. the ice core's annual layer thickness record.
To estimate the impact of the obtained best-fit HL profile on the estimation of the SMB record derived, we extract the density profile obtained at the closest location to the ice core site, for each ice rise, which we then compare to the ice core density profiles (raw and exponential fit, see Data sets section and Supplement S1). We observe that the HL and exponential fits are reasonably close for the 10–50 m depth interval, in particular for LIR and HIR (Supplementary Fig. S4). For DIR, the difference is larger, which is likely a result of how we had to derive the ‘equivalent’ ice core location. The difference between the exponential and HL best-fit is less negligible for the interval between the surface and the first IRH. Near the surface, the HL profile is a linear fit which is a crude approximation of how densification occurs in the first meters below the surface (Cuffey and Paterson, Reference Cuffey and Paterson2010). Equally, the exponential fit of the raw ice core densities is poorer near the surface where density changes more rapidly. This implies that the error on the surface SMB calculated is larger for the first time interval than for the following time intervals, i.e. we likely overestimate the surface SMB, using both the HL radar-derived fit and the exponential ice core-derived fit of depth-density. The impact of this overestimation is negligible, as discussed in the Results section.
3.4. Obtaining a gridded radar SMB data product
In order to reduce the impact of different radar data coverage between ice rises on our results, we homogenize the radar-derived SMB record spatially and restrict the data to the same surface before calculating the average SMB over the radar surveys. The first step is to obtain a gridded SMB radar product for each ice rise, centered on the ice core location. The gridded SMB radar product is calculated for two different grid resolutions: a $50\times 50$![]() m and a $10\times 10$
m and a $10\times 10$![]() m resolution. All radar data points that fall within a grid cell are averaged over that grid cell. A missing value is retained if no data are available in one grid cell. The second step is to restrict the gridded radar SMB data to the same surface area for each ice core site. We only keep the data grid points that fall within a certain radial distance of each ice core site, for four different radial distances. We start from a maximum radial distance away from the ice core site that still retains approximately homogeneous spatial radar coverage across the quadrants (which equates to 4500, 3600 and 4000 m for DIR, LIR and HIR, respectively, Supplementary Fig. S9), then decrease to 2500 m (to approximate the RACMO2.3 5.5 km RCM grid cell size), 500 m and finally 200 m. For the two largest surface areas, we use the $50\times 50$
m resolution. All radar data points that fall within a grid cell are averaged over that grid cell. A missing value is retained if no data are available in one grid cell. The second step is to restrict the gridded radar SMB data to the same surface area for each ice core site. We only keep the data grid points that fall within a certain radial distance of each ice core site, for four different radial distances. We start from a maximum radial distance away from the ice core site that still retains approximately homogeneous spatial radar coverage across the quadrants (which equates to 4500, 3600 and 4000 m for DIR, LIR and HIR, respectively, Supplementary Fig. S9), then decrease to 2500 m (to approximate the RACMO2.3 5.5 km RCM grid cell size), 500 m and finally 200 m. For the two largest surface areas, we use the $50\times 50$![]() m gridded SMB radar product, and for the two smallest we use the $10\times 10$
m gridded SMB radar product, and for the two smallest we use the $10\times 10$![]() m SMB product.
m SMB product.
3.5. SMB uncertainties
For the radar-derived SMB, the uncertainty is calculated as the root-mean-square-error of the percentage SMB errors due to density uncertainties and to depth uncertainties, for each ice rise. Density uncertainties arise from the HL approximation used to obtain a depth-density profile at each radar trace, as we only have direct depth-density measurements at the ice core sites. We quantify the uncertainty that arises from this approximation as the standard deviation of all HL best-fit profiles over the entire radar survey, for each ice rise, following previous approaches (Medley and others, Reference Medley2013; Kausch and others, Reference Kausch2020). The depth uncertainty arises from the radar system bandwidth used to collect the radar data, which determine the highest vertical resolution that can be achieved (2.5 ns in the time domain and $\sim 21$![]() cm in the depth domain). The root-mean-square SMB error is then cumulated over the IRH depths as SMB values are always calculated as a cumulative mass from the surface. The resulting radar-derived SMB uncertainties calculated increase with depth. Across all three ice rises, the radar-derived SMB uncertainty is between 2 and 4% of the SMB record for the shallowest IRH pair, and between 6 and 7% of the SMB record for the deepest IRH pair. It should be noted that all HL simulations are using the same surface density of 0.434 g cm$^{-3}$
cm in the depth domain). The root-mean-square SMB error is then cumulated over the IRH depths as SMB values are always calculated as a cumulative mass from the surface. The resulting radar-derived SMB uncertainties calculated increase with depth. Across all three ice rises, the radar-derived SMB uncertainty is between 2 and 4% of the SMB record for the shallowest IRH pair, and between 6 and 7% of the SMB record for the deepest IRH pair. It should be noted that all HL simulations are using the same surface density of 0.434 g cm$^{-3}$![]() . However, 2.5% surface snow density variability has been documented at the Blåskimen Island ice rise further west along the coast (Goel and others, Reference Goel, Brown and Matsuoka2017, Reference Goel, Martin and Matsuoka2018), while recent snow micro pen density measurements indicate a 5 and 13% maximum surface snow variability at LIR and HIR at 50 cm depth, respectively (N. Wever, pers. comm., 2022). The uncertainty in the surface density is thus estimated to be of the order of 10%. We have examined the influence of a change in $\pm$
. However, 2.5% surface snow density variability has been documented at the Blåskimen Island ice rise further west along the coast (Goel and others, Reference Goel, Brown and Matsuoka2017, Reference Goel, Martin and Matsuoka2018), while recent snow micro pen density measurements indicate a 5 and 13% maximum surface snow variability at LIR and HIR at 50 cm depth, respectively (N. Wever, pers. comm., 2022). The uncertainty in the surface density is thus estimated to be of the order of 10%. We have examined the influence of a change in $\pm$![]() 10% in the surface density on the best-fit HL profile and the SMB and concluded that it has a negligible impact on our main results, discussed below, on the representativeness of a pointwise measurement in terms of mean and temporal variability of the SMB signal, at either of the three ice rises. For the ice core SMB, the uncertainty is dominated by the density measurement errors, assessed to be 4% throughout the column at DIR (Hubbard and others, Reference Hubbard2013). We assume this is a valid and conservative estimate for the LIR and HIR ice cores as well. We do not take into consideration the ice core dating error in our SMB uncertainties for the ice core SMB and the radar-derived SMB as this is an absolute uncertainty which affects both records equally and therefore does not inform on range of differences in SMB that can be observed between radar-derived and ice core SMB. In other words, the age uncertainty is important, but not for the estimate of spatial representativity proposed here.
10% in the surface density on the best-fit HL profile and the SMB and concluded that it has a negligible impact on our main results, discussed below, on the representativeness of a pointwise measurement in terms of mean and temporal variability of the SMB signal, at either of the three ice rises. For the ice core SMB, the uncertainty is dominated by the density measurement errors, assessed to be 4% throughout the column at DIR (Hubbard and others, Reference Hubbard2013). We assume this is a valid and conservative estimate for the LIR and HIR ice cores as well. We do not take into consideration the ice core dating error in our SMB uncertainties for the ice core SMB and the radar-derived SMB as this is an absolute uncertainty which affects both records equally and therefore does not inform on range of differences in SMB that can be observed between radar-derived and ice core SMB. In other words, the age uncertainty is important, but not for the estimate of spatial representativity proposed here.
4. Results
4.1. SMB spatial distribution
We observe the same spatial pattern of SMB for each time interval examined, and for each ice rise, with higher SMB values always found on the windward (eastern) side of the ice rises and lower values on the leeward (western) side (Figs 2 and 3 for HIR, and Supplementary Figs S5–S8 for DIR and LIR). In addition, the crest at each ice rise is characterized by a localized minimum in SMB. This spatial pattern is visible in the IRH geometries with the IRH depths highest on the windward side and lowest on the leeward side of each ice rise (Fig. 2, panel a).

Fig. 2. IRH depth and SMB obtained at HIR (Fig. 1). (a) Depth of the shallowest IRH. A star locates the ice core site and the mean wind direction is shown by black arrows (RACMO2.3 5.5 km simulations over 1979–2017, Lenaerts and others (Reference Lenaerts2017); Van Wessem and others (Reference Van Wessem2018)). Contours shown are REMA elevations at 20 m intervals (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). (b) SMB obtained along the radar transect shown in the inset. Each colored line indicates a different IRH. The windward sides of the ice rise are highlighted in light blue and the ice divide intersections are marked by blue vertical lines. The inset displays the whole radar survey at HIR with the radar transect shown in blue with magenta crosses indicating the divide intersections, green and red dots indicating the start and end of the radar transect, respectively, a yellow star locating the ice core site. Related figures for DIR and LIR are found in Supplementary Figures S5 and S7.

Fig. 3. SMB (cm w.e. a$^{-1}$![]() ) calculated per time interval at HIR (indicated on each inset) for the gridded data set ($50\times 50$
) calculated per time interval at HIR (indicated on each inset) for the gridded data set ($50\times 50$![]() m). The corresponding ice core SMB value is shown by a star on the same color scale as for the radar transects. Contours shown are REMA elevations at 20 m intervals (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Mean wind direction is shown by black arrows (RACMO2.3 5.5 km simulations over 1979–2017, Lenaerts and others (Reference Lenaerts2017); Van Wessem and others (Reference Van Wessem2018)). Related figures for DIR and LIR are found in Supplementary Figures S6 and S8.
m). The corresponding ice core SMB value is shown by a star on the same color scale as for the radar transects. Contours shown are REMA elevations at 20 m intervals (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Mean wind direction is shown by black arrows (RACMO2.3 5.5 km simulations over 1979–2017, Lenaerts and others (Reference Lenaerts2017); Van Wessem and others (Reference Van Wessem2018)). Related figures for DIR and LIR are found in Supplementary Figures S6 and S8.
The gradient observed here in SMB is consistent with the results of previous studies on these three ice rises (Drews and others, Reference Drews2015; Kausch and others, Reference Kausch2020) and for ice rises in the region in general (Lenaerts and others, Reference Lenaerts2014; Matsuoka and others, Reference Matsuoka2015; Goel and others, Reference Goel, Brown and Matsuoka2017; Pratap and others, Reference Pratap2021). At DIR, Drews and others (Reference Drews2015) described a cross-divide windward-to-leeward spatial gradient in SMB, averaged over 21 years at DIR before 2012. Kausch and others (Reference Kausch2020) showed the same spatial gradient at a decadal resolution over $\sim 30$![]() years at LIR and averaged over 16 years at HIR. Our results indicate that this remains true at the sub-decadal temporal resolution, over the course of $\sim 50-60$
years at LIR and averaged over 16 years at HIR. Our results indicate that this remains true at the sub-decadal temporal resolution, over the course of $\sim 50-60$![]() years. The dominant winds along the Princess Ragnhild Coast that are associated with synoptic storms deliver most of their moisture as they flow up the eastern face of the ice rises, resulting in a drier western side. This spatial SMB contrast is potentially enhanced and redistributed through wind-driven erosion and redeposition of surface snow (King and others, Reference King2004; Kausch and others, Reference Kausch2020). Kausch and others (Reference Kausch2020) have shown that the localized SMB minimum observed at the crest of each ice rise is due to wind erosion (see also King and others, Reference King2004, for the Lyddan ice rise). This spatial pattern of SMB remains quite stationary through time, and across all three ice rises, regardless of whether they have a simple divide (DIR and LIR) or a triple junction divide (HIR). We note that at HIR, the highest accumulation is found to the south of the summit of the ice rise, which could be linked to the interaction between katabatic winds descending from further south and the unique triple divide geometry of HIR.
years. The dominant winds along the Princess Ragnhild Coast that are associated with synoptic storms deliver most of their moisture as they flow up the eastern face of the ice rises, resulting in a drier western side. This spatial SMB contrast is potentially enhanced and redistributed through wind-driven erosion and redeposition of surface snow (King and others, Reference King2004; Kausch and others, Reference Kausch2020). Kausch and others (Reference Kausch2020) have shown that the localized SMB minimum observed at the crest of each ice rise is due to wind erosion (see also King and others, Reference King2004, for the Lyddan ice rise). This spatial pattern of SMB remains quite stationary through time, and across all three ice rises, regardless of whether they have a simple divide (DIR and LIR) or a triple junction divide (HIR). We note that at HIR, the highest accumulation is found to the south of the summit of the ice rise, which could be linked to the interaction between katabatic winds descending from further south and the unique triple divide geometry of HIR.
4.2. Quantifying ice core SMB representativeness
The focus of our study is not on detailing the SMB temporal evolution based on these data sets. Our outcome is to quantify the limited area over which the ice cores are representative, as we do not expect the cores to represent a large area based on the previous studies detailed above. For this, we use the radar SMB records obtained from the IRH depths and age, averaged over the radar survey of the ice rise, to determine at what spatial scale the mean radar SMB records match those of the ice core.
At first glance, the SMB signal measured at the ice core site is representative of a small surface area. The SMB changes rapidly as we move away from the core site, with SMB gradients varying between $\sim 6$![]() and 12 cm w.e. yr$^{-1}$
and 12 cm w.e. yr$^{-1}$![]() per km across the three ice rises (Figs 2 and 3 for HIR, and supplementary Figs S5–S8 for DIR and LIR). To evaluate the representativeness of the ice core SMB for the entirety of the ice rise, we compare the ice core measured SMB signal to the radar-derived SMB averaged over the whole radar survey, for each ice rise. We first examine the difference between the mean SMB for the ice core and the average radar records. We then inspect the difference in the SMB temporal variability of these two records. We note that when we refer to temporal variability hereafter, we imply multi-annual to decadal variability, which can be resolved using the radar-derived SMB obtained.
per km across the three ice rises (Figs 2 and 3 for HIR, and supplementary Figs S5–S8 for DIR and LIR). To evaluate the representativeness of the ice core SMB for the entirety of the ice rise, we compare the ice core measured SMB signal to the radar-derived SMB averaged over the whole radar survey, for each ice rise. We first examine the difference between the mean SMB for the ice core and the average radar records. We then inspect the difference in the SMB temporal variability of these two records. We note that when we refer to temporal variability hereafter, we imply multi-annual to decadal variability, which can be resolved using the radar-derived SMB obtained.
We observe that, for each ice rise, the SMB measured at the ice core site is smaller than the mean SMB for the whole ice rise (Fig. 4). On average, the mean value over the whole ice rise is $\sim 18-40\percnt$![]() larger than the SMB measured at the ice core site over the whole time period studied across all three ice rises. If we only consider the radar data oriented towards the dominant wind direction (dark red curve on Fig. 4), approximated by averaging SMB from the radar transect sections east of the ice rise crest, the SMB difference between the pointwise SMB value at the ice core site and the survey average is exacerbated, as expected, with the survey average being $\sim 23-47\percnt$
larger than the SMB measured at the ice core site over the whole time period studied across all three ice rises. If we only consider the radar data oriented towards the dominant wind direction (dark red curve on Fig. 4), approximated by averaging SMB from the radar transect sections east of the ice rise crest, the SMB difference between the pointwise SMB value at the ice core site and the survey average is exacerbated, as expected, with the survey average being $\sim 23-47\percnt$![]() larger than the SMB measured at the ice core site. If we now only consider the radar data oriented away from the dominant wind direction (light red curve on Fig. 4), approximated by averaging SMB from the radar transect sections west of the ice rise crest, the difference is less strong, with the survey average now only $\sim 10-39\percnt$
larger than the SMB measured at the ice core site. If we now only consider the radar data oriented away from the dominant wind direction (light red curve on Fig. 4), approximated by averaging SMB from the radar transect sections west of the ice rise crest, the difference is less strong, with the survey average now only $\sim 10-39\percnt$![]() larger than the mean ice core SMB. Considering that the radar-derived SMB uncertainties and the ice core uncertainties reach up to 7% and 4% of the SMB, respectively, the difference in the mean state of the SMB signal observed between a point measurement and the whole area average for all three ice rises is larger than the uncertainties and therefore robust. A pointwise measurement of SMB at the crest of the ice rise, at least across these three ice rises and at the multi-annual to decadal time resolution examined here, is thus consistently smaller than the whole ice rise's mean value.
larger than the mean ice core SMB. Considering that the radar-derived SMB uncertainties and the ice core uncertainties reach up to 7% and 4% of the SMB, respectively, the difference in the mean state of the SMB signal observed between a point measurement and the whole area average for all three ice rises is larger than the uncertainties and therefore robust. A pointwise measurement of SMB at the crest of the ice rise, at least across these three ice rises and at the multi-annual to decadal time resolution examined here, is thus consistently smaller than the whole ice rise's mean value.

Fig. 4. SMB evolution for (a) HIR, (b) DIR and (c) LIR measured in the ice core (thick blue line, using the exponential fit of the raw core density data, see Methods), calculated from the radar survey average (thick red line). Windward-only and leeward-only radar survey averages are shown in dark and light red, respectively. The radar-derived SMB extracted at the closest point to the ice core site is shown in magenta. The difference between the radar-derived SMB and ice core measured SMB is given on each panel for the mean and the temporal variability (given as the standard deviation of the difference of the radar and ice core SMB residuals).
If we look at the SMB obtained from the radar point closest to the ice core site (magenta curve on Fig. 4), we see that the difference in SMB mean state is much smaller, calculated to be between $\sim 1$![]() % and 5% of the ice core SMB signal, which is insignificant considering the SMB uncertainties. Note that the difference between the SMB signal at the “equivalent” ice core location and the ice core site is largest at DIR; we suspect it arises from the way the “equivalent” ice core location is obtained (see Methods section).
% and 5% of the ice core SMB signal, which is insignificant considering the SMB uncertainties. Note that the difference between the SMB signal at the “equivalent” ice core location and the ice core site is largest at DIR; we suspect it arises from the way the “equivalent” ice core location is obtained (see Methods section).
We next examine the representativeness of the ice core for the larger ice rise area in terms of temporal variability (i.e., multi-annual to decadal variability). For this, we calculate the standard deviation of the difference between the average of the radar survey SMB anomaly (i.e., radar-derived SMB minus the long term radar SMB average) and the ice core SMB anomaly (i.e., ice core SMB minus the long term ice core SMB average for the same time intervals as the radar SMB), for each ice rise (given on each panel of Fig. 4). We obtain a standard deviation that ranges between $\sim 2.0$![]() and 4.4 cm w.e. a$^{-1}$
and 4.4 cm w.e. a$^{-1}$![]() across the three ice rises, which corresponds to $\sim 3-12\percnt$
across the three ice rises, which corresponds to $\sim 3-12\percnt$![]() of the mean ice core SMB. The difference in temporal variability between the radar survey average and the ice core signal is therefore inferior to the radar-derived SMB uncertainties (except at LIR with a 12% difference), indicating that the temporal variability is generally well represented in pointwise measurements at the crest of these ice rises.
of the mean ice core SMB. The difference in temporal variability between the radar survey average and the ice core signal is therefore inferior to the radar-derived SMB uncertainties (except at LIR with a 12% difference), indicating that the temporal variability is generally well represented in pointwise measurements at the crest of these ice rises.
Note that the fact that SMB is overestimated for the first time interval (between the surface and the first IRH, due to the approximations used to calculate densities for both the ice core-derived and the radar survey average SMB) has a negligible impact on our results. We recalculated mean SMB and SMB temporal variability of the ice core SMB and the radar-derived SMB while omitting this first time interval and the percentage differences between the ice core SMB and the radar-derived SMB were changed by a percent or less.
4.3. Representativeness as a function of the area
To quantify more precisely the influence of the surface area chosen on the difference with a pointwise SMB measurement at the top of the ice rise, we incrementally restrict our radar survey coverage for each ice rise ‘artificially’ to observe the impact on the difference in mean state and temporal variability of the SMB obtained. Because the radar surveys do not have the same coverage at each ice rise (differing survey design, survey line density, proportion of radar transects covering the windward/leeward sides of the ice rise, etc), we first resample the radar data on the same regular grid so that we can compare our results at each ice rise directly (see Methods section). Using the resulting gridded radar SMB product, for each of the four incrementally decreasing surface areas, we then calculate the radar survey mean SMB, as before, which we compare to the SMB measured at the ice core site, and this for each ice rise (Fig. 5 for HIR, Supplementary Figs S10 and S11 for DIR and LIR, respectively). We indicate the difference between the gridded mean SMB and the pointwise ice core SMB mean, as well as the difference in temporal variability of the two SMB signals on each panel of Figures 5, S7 and S8 (measured as the standard deviation of the difference of the radar and ice core SMB residuals). Note that to ensure a more even distribution of SMB data across windward and leeward areas at each ice rise, the spatial mean of the radar SMB is calculated by first averaging the gridded SMB radar product per quadrant (the radial areas are split into 8$^{ths}$![]() ) before averaging across all eight quadrant averages obtained. We note however that the results are effectively identical if this spatial averaging per quadrant is not done beforehand.
) before averaging across all eight quadrant averages obtained. We note however that the results are effectively identical if this spatial averaging per quadrant is not done beforehand.

Fig. 5. SMB record measured from the ice core (blue line) versus the gridded radar survey mean for decreasing radial distances from the ice core site (red line), for HIR. Each panel indicates the mean state difference and the standard deviation of the temporal variability (given as the difference of the radar and ice core SMB residuals). SMB uncertainty bounds for each record are outlined as dotted lines. Related figures for DIR and LIR are found in Supplementary Figures S10 and S11.
We observe that the mean difference between the area average and the pointwise measurement reduces as the considered surface area decreases. This is clearly visible for HIR and LIR where the mean SMB difference decreases from 6.8 cm w.e. a$^{-1}$![]() for the largest surface area considered to 1.4 cm w.e. a$^{-1}$
for the largest surface area considered to 1.4 cm w.e. a$^{-1}$![]() for the smallest surface area, and from 12.8 to $\sim 1.0$
for the smallest surface area, and from 12.8 to $\sim 1.0$![]() cm w.e. yr$^{-1}$
cm w.e. yr$^{-1}$![]() , respectively. This implies that the difference between the pointwise SMB measurement and the area mean shrinks from $\sim 19$
, respectively. This implies that the difference between the pointwise SMB measurement and the area mean shrinks from $\sim 19$![]() to 4% of the ice core SMB signal at HIR, and from $\sim 34$
to 4% of the ice core SMB signal at HIR, and from $\sim 34$![]() to $\sim 3\percnt$
to $\sim 3\percnt$![]() at LIR. We consider that a pointwise measurement of SMB is representative when the difference between the pointwise SMB measurement and the area mean is negligible with respect to the SMB uncertainties calculated (minimum of 2% for shallow IRH pairs and up to a maximum of 7% for deep IRH pairs, see SMB uncertainties section). For the ice rises that we study here, we conclude that a pointwise measurement of SMB such as an ice core is representative of the mean SMB of $\sim 500$
at LIR. We consider that a pointwise measurement of SMB is representative when the difference between the pointwise SMB measurement and the area mean is negligible with respect to the SMB uncertainties calculated (minimum of 2% for shallow IRH pairs and up to a maximum of 7% for deep IRH pairs, see SMB uncertainties section). For the ice rises that we study here, we conclude that a pointwise measurement of SMB such as an ice core is representative of the mean SMB of $\sim 500$![]() m radial surface area for older SMB time interval and of $\sim 200$
m radial surface area for older SMB time interval and of $\sim 200$![]() m radial surface area for younger SMB time intervals. The conclusions are less clear at DIR where the mean SMB difference does not decrease significantly: the mean ice core-radar SMB offset reduces from 11.8 cm w.e. a$^{-1}$
m radial surface area for younger SMB time intervals. The conclusions are less clear at DIR where the mean SMB difference does not decrease significantly: the mean ice core-radar SMB offset reduces from 11.8 cm w.e. a$^{-1}$![]() for a radial distance of 4500 m to 10.9 cm w.e. a$^{-1}$
for a radial distance of 4500 m to 10.9 cm w.e. a$^{-1}$![]() for a radial distance of 500 m, corresponding to a mean SMB difference that shrinks from $\sim 20$
for a radial distance of 500 m, corresponding to a mean SMB difference that shrinks from $\sim 20$![]() to $\sim 19\percnt$
to $\sim 19\percnt$![]() of the DIR ice core SMB signal. However, the smallest radial distance we use at DIR is 500 m, and even within a 500 m radius of the ice core site, the number of radar observations remains very low at DIR compared to that at HIR or LIR (Supplementary Fig. S9).
of the DIR ice core SMB signal. However, the smallest radial distance we use at DIR is 500 m, and even within a 500 m radius of the ice core site, the number of radar observations remains very low at DIR compared to that at HIR or LIR (Supplementary Fig. S9).
We next examine the difference in SMB temporal variability between the point measurements and the area-wide averages for the four decreasing surface areas. Again, we stress that the temporal variability here refers to multi-annual to decadal variability. As for the mean differences, we note that as the surface area considered decreases, the difference in SMB temporal variability between the point measurements and the area-wide averages also decreases. However, the SMB temporal variability difference remains negligible with respect to the ice core and radar SMB uncertainties. At HIR, the difference in SMB temporal variability between the area-wide average and the pointwise measurement is 2.4 cm w.e. a$^{-1}$![]() at a radius of 4 km from the ice core site, and 1.8 cm w.e. a$^{-1}$
at a radius of 4 km from the ice core site, and 1.8 cm w.e. a$^{-1}$![]() at a radius of 200 m, which corresponds to 6 and 5% of the ice core's mean SMB record. The difference in temporal variability between the radar survey averages and the ice core records is therefore negligible with respect to the SMB uncertainties evaluated, whatever the surface area considered. The same is mostly true at LIR, which shows a difference in temporal variability that corresponds 8–3% of the ice core's mean SMB record at a radius of 4 km and 200 m from the ice core site, respectively (Supplementary Fig. S11). At DIR, a difference in temporal variability corresponds to 3% of the ice core's mean SMB record at a radius of 4.5 and 2.5 km from the ice core site, so negligible with respect to the SMB uncertainties. The difference in temporal variability actually increases by $\sim 1\percnt$
at a radius of 200 m, which corresponds to 6 and 5% of the ice core's mean SMB record. The difference in temporal variability between the radar survey averages and the ice core records is therefore negligible with respect to the SMB uncertainties evaluated, whatever the surface area considered. The same is mostly true at LIR, which shows a difference in temporal variability that corresponds 8–3% of the ice core's mean SMB record at a radius of 4 km and 200 m from the ice core site, respectively (Supplementary Fig. S11). At DIR, a difference in temporal variability corresponds to 3% of the ice core's mean SMB record at a radius of 4.5 and 2.5 km from the ice core site, so negligible with respect to the SMB uncertainties. The difference in temporal variability actually increases by $\sim 1\percnt$![]() from 3% at a 2.5 km radius to 4% at a 500 m radius, but the number of radar observations at a 500 m radius is certainly too low to inform on SMB variability (Fig. S10).
from 3% at a 2.5 km radius to 4% at a 500 m radius, but the number of radar observations at a 500 m radius is certainly too low to inform on SMB variability (Fig. S10).
4.4. SMB temporal variability as a function of the location
Finally, we examine how temporal variability varies across each ice rise from the spatial distribution of the radar-derived SMB anomalies (radar-derived SMB minus the long-term radar SMB average). In particular, we want to determine if periods with high mean SMB balance correspond to a homogeneous increase over the area covered by the radar survey or if positive and negative anomalies are present and compensate each other in the computation of the mean value that was compared in the previous section with the SMB derived from the ice core. We calculate the variations for each radar SMB time interval (Fig. 6 for HIR, and Supplementary FigsS12 and S13 for DIR and LIR, respectively). We use the $50\times 50$![]() m gridded radar product at the largest radial distance away from each ice core site. The survey mean, and standard deviation, of the radar SMB anomaly for each time interval is displayed on each panel of Figures 6, S12 and S13. We can see that, at this multi-annual to decadal timescale, the SMB anomaly is entirely positive or entirely negative over the whole ice rise, for all time intervals (except those with a low average value, e.g. panels 2012–2008 and 1994–1982 in Fig. 6 for HIR). We also observe that the ice core SMB anomaly (color of the star in Fig. 6) matches qualitatively well to the radar-derived SMB anomalies at most locations (again except for the time intervals with a low average SMB anomaly value).
m gridded radar product at the largest radial distance away from each ice core site. The survey mean, and standard deviation, of the radar SMB anomaly for each time interval is displayed on each panel of Figures 6, S12 and S13. We can see that, at this multi-annual to decadal timescale, the SMB anomaly is entirely positive or entirely negative over the whole ice rise, for all time intervals (except those with a low average value, e.g. panels 2012–2008 and 1994–1982 in Fig. 6 for HIR). We also observe that the ice core SMB anomaly (color of the star in Fig. 6) matches qualitatively well to the radar-derived SMB anomalies at most locations (again except for the time intervals with a low average SMB anomaly value).

Fig. 6. Spatial distribution of the SMB anomalies at HIR. For the ice core (indicated by a colored star), it is simply the SMB measured from which the temporal mean is removed. For the radar survey, we use the $50\times 50$![]() m gridded radar product for a radius of 4 km away from the ice core site. For each grid cell, we calculate the SMB anomaly by subtracting the temporal mean from the calculated SMB record. The spatial mean, and standard deviation, of the radar SMB anomalies for each time interval is displayed on each panel. Contours shown are REMA elevations at 20 m intervals (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Related figures for DIR and LIR are found in Supplementary Figures S12 and S13.
m gridded radar product for a radius of 4 km away from the ice core site. For each grid cell, we calculate the SMB anomaly by subtracting the temporal mean from the calculated SMB record. The spatial mean, and standard deviation, of the radar SMB anomalies for each time interval is displayed on each panel. Contours shown are REMA elevations at 20 m intervals (Howat and others, Reference Howat, Porter, Smith, Noh and Morin2019). Related figures for DIR and LIR are found in Supplementary Figures S12 and S13.
5. Discussion
Our results indicate that the SMB record recovered in ice cores, drilled on the crest of the ice rises of the region, is only representative of the specific location where it was collected when we examine the SMB mean state. For the three ice rises studied here, the ice core records, drilled at the ice rises’ crests, are representative of the mean SMB in a $\sim 200--500$![]() m radius from where they were drilled (depending on the time interval considered). The difference between the area mean SMB and the ice core measured SMB quickly increases with distance away from the ice core site. This mean state difference is already larger than the radar-derived SMB uncertainty when a radial distance of $\sim 2.5$
m radius from where they were drilled (depending on the time interval considered). The difference between the area mean SMB and the ice core measured SMB quickly increases with distance away from the ice core site. This mean state difference is already larger than the radar-derived SMB uncertainty when a radial distance of $\sim 2.5$![]() km from the ice core site is considered: 16% of the ice core's SMB record at HIR, 33% at LIR and 22% at DIR. This can be relevant when we consider, e.g. RCM SMB simulation results for which the grid resolution is on the order of $5\times 5$
km from the ice core site is considered: 16% of the ice core's SMB record at HIR, 33% at LIR and 22% at DIR. This can be relevant when we consider, e.g. RCM SMB simulation results for which the grid resolution is on the order of $5\times 5$![]() km at best. A radial distance of 2.5 km from the ice core site is relatively close to the grid size of polar-tuned regional climate models such as RACMO (Van Wessem and others, Reference Van Wessem2014; Lenaerts and others, Reference Lenaerts2017; Van Wessem and others, Reference Van Wessem2018) or MAR (Agosta and others, Reference Agosta2019). The SMB mean state of a whole ice rise is therefore not well represented in a single pointwise measurement. However, co-located radar data can be used to evaluate the shift that needs to be applied to the ice core SMB record so that it becomes representative of the mean over the whole ice rise. The magnitude of the shift can simply be obtained from the difference in mean states between the radar survey average SMB and the ice core SMB record over the overlap period. We determine that the mean SMB measured at a pointwise location, such as in an ice core, is representative of a relatively small surface area. There is a systematic shift of $\sim 7-15$
km at best. A radial distance of 2.5 km from the ice core site is relatively close to the grid size of polar-tuned regional climate models such as RACMO (Van Wessem and others, Reference Van Wessem2014; Lenaerts and others, Reference Lenaerts2017; Van Wessem and others, Reference Van Wessem2018) or MAR (Agosta and others, Reference Agosta2019). The SMB mean state of a whole ice rise is therefore not well represented in a single pointwise measurement. However, co-located radar data can be used to evaluate the shift that needs to be applied to the ice core SMB record so that it becomes representative of the mean over the whole ice rise. The magnitude of the shift can simply be obtained from the difference in mean states between the radar survey average SMB and the ice core SMB record over the overlap period. We determine that the mean SMB measured at a pointwise location, such as in an ice core, is representative of a relatively small surface area. There is a systematic shift of $\sim 7-15$![]() cm w.e. a $^{-1}$
cm w.e. a $^{-1}$![]() between what is measured in the ice core and the ice rise's surveyed area average (evaluated from the co-located radar data). This difference corresponds to $\sim 18-40\percnt$
between what is measured in the ice core and the ice rise's surveyed area average (evaluated from the co-located radar data). This difference corresponds to $\sim 18-40\percnt$![]() of the ice core's mean SMB signal. This indicates that we can adjust the measured ice core SMB values by shifting the absolute mean according to the radar-ice core mean difference. This shifted records would thus include interannual variations over a long period, which is a main interest of ice core records, with a mean value representative of a greater area. Adding an additional single point measurement, even a few tens of meters apart, does not provide information on the larger area SMB average (see radar point closest to the ice core site, Fig. 4). This suggests that drilling several ice cores in close proximity is therefore not a simple solution to improve ice core representativeness.
of the ice core's mean SMB signal. This indicates that we can adjust the measured ice core SMB values by shifting the absolute mean according to the radar-ice core mean difference. This shifted records would thus include interannual variations over a long period, which is a main interest of ice core records, with a mean value representative of a greater area. Adding an additional single point measurement, even a few tens of meters apart, does not provide information on the larger area SMB average (see radar point closest to the ice core site, Fig. 4). This suggests that drilling several ice cores in close proximity is therefore not a simple solution to improve ice core representativeness.
On the other hand, in terms of temporal variability of the SMB signal, our results show that, for the three ice rises studied here, the ice core record is well representative of the whole ice rise, for multi-annual to decadal variability. At HIR and LIR, the difference in SMB temporal variability between the area mean SMB and the ice core measured SMB varies between 3 and 8% of the ice core's mean SMB record over all the radial distances from the ice core sites considered. The difference in temporal variability between the radar survey averages and the ice core records is therefore negligible with respect to the SMB uncertainties evaluated. This seems to indicate that ice cores drilled at the crest of these ice rises contain a record of multi-annual to decadal variability that can be trusted, whatever the surface area considered, as evidenced in the relatively constant temporal variability across all radii considered.
We note that the radar surveys used here do not cover the whole ice rises and so we recognize that our conclusions could be slightly different if radar coverage was more extensive. However, Pratap and others (Reference Pratap2021) show that at the Leningradkollen Ice Rise, another ice rise located along the Princess Ragnhild Coast $\sim 340$![]() km to the west of HIR, there is also a large difference in mean SMB between the radar survey mean and the ice core SMB measured despite the very extensive radar coverage of the whole ice rise. In addition, our results agree well across the three ice rises studied, even before gridding the radar-derived SMB, which implies that the survey design across the ice rises has a relatively small incidence on the results. We also note that our results are dependent on where the ice cores are drilled. The SMB record preserved at the ice core site is a function of the meteorological and glaciological conditions locally. For these three ice rises, the ice cores were drilled in the center of the ice rises, on their crest.
km to the west of HIR, there is also a large difference in mean SMB between the radar survey mean and the ice core SMB measured despite the very extensive radar coverage of the whole ice rise. In addition, our results agree well across the three ice rises studied, even before gridding the radar-derived SMB, which implies that the survey design across the ice rises has a relatively small incidence on the results. We also note that our results are dependent on where the ice cores are drilled. The SMB record preserved at the ice core site is a function of the meteorological and glaciological conditions locally. For these three ice rises, the ice cores were drilled in the center of the ice rises, on their crest.
Finally, the spatial homogeneity of the SMB temporal anomalies observed at each ice rise and for each time interval suggests that, for the ice rises examined in this study, the snow events generally blanket the whole ice rise. The presence of storms induces a homogeneous positive SMB temporal variability, while the absence of storms induces a homogeneous negative SMB temporal variability at this multi-annual to decadal resolution. The temporal variability of the SMB signal is nicely synchronized over these three ice rises, and does not seem to be affected by wind redistribution, as opposed to the spatial variability of the mean state (windward-leeward SMB gradient). This spatial homogeneity of the multi-annual to decadal SMB variability is another indication therefore that a pointwise measurement is sufficient to quantify the entire ice rise's temporal variability of SMB, at least for this specific region and the multi-annual to decadal timescale.
Radar-derived SMB is increasingly used to compare to RCM output (Medley and others, Reference Medley2013, Reference Medley2018; Dattler and others, Reference Dattler, Lenaerts and Medley2019; Kausch and others, Reference Kausch2020; Pratap and others, Reference Pratap2021) and provides detailed spatial constraints on SMB. Using the mean of the radar-derived SMB obtained for each radar survey collected, or a sufficiently large surface area, could allow us to create a single SMB time series that is representative of a region whose size is similar to the grid size of the model. The ice core data provide complementary information on inter-annual variations that cannot be resolved by most radar surveys. Combining radar and ice core measurements in model-data comparisons is therefore a very promising approach. On the one hand, we could think of creating multiple averages of the radar-derived SMB over areas similar to the grid size of the models to compare these multiple time series to RCM outputs. The RACMO RCM for example, at the 5.5 km resolution, has an overlap between four to eight grid cells with the radar surveys over these three ice rises, which could then be compared to four to eight SMB time series. Going further, we could compare these SMB time series to GCM outputs to track potential discrepancies induced by the coarser spatial resolution of the latter. On the other hand, adjusting the values of the ice cores using the mean radar-ice SMB discrepancy (as opposed to using the radar data directly) would provide a single time-series of SMB at a higher resolution (annual) that would be representative of an area of $\sim 50-100$![]() km$^{2}$
km$^{2}$![]() , over longer time scales. To compare to model output or to large-scale SMB studies, it is much easier to use a single time series than referring back to the radar data, even if the radar data do provide rich spatial information. Similarly, in addition to RCMs, we might think of comparing GCM outputs to the adjusted SMB record.
, over longer time scales. To compare to model output or to large-scale SMB studies, it is much easier to use a single time series than referring back to the radar data, even if the radar data do provide rich spatial information. Similarly, in addition to RCMs, we might think of comparing GCM outputs to the adjusted SMB record.
6. Conclusion
We have examined three ice rises located along the Princess Ragnhild Coast in East Antarctica. Synoptic-scale systems transport moisture-loaded air to the region from the Southern Ocean. Orographic lifting on the windward (eastern) side of the ice rises leads to high snowfall rates there, while a precipitation shadow leaves the leeward (western) side much drier. This is visible in both the radar IRH depths measured, which are generally deeper on the windward sides than the leeward sides, and the SMB rates calculated from the dated radar stratigraphy interpreted on each ice rise, with generally higher SMB on the windward sides than the leeward sides. Wind-driven remobilization of the accumulated snow by katabatic winds can modify this SMB spatial gradient.
The homogeneous spatial signature of the SMB temporal anomalies indicates a uniform deposition of snow, which is either higher than average, or lower than average, over the entire ice rises. It confirms that any temporal variability of the SMB over the ice rise is represented similarly everywhere, therefore a pointwise measurement is sufficient to obtain a realistic estimation of the regional SMB multi-annual to decadal variability.
We conclude that, if the intention is to use ice core SMB records to assess regional SMB or compare to RCM simulations, these records need to be adjusted to be more representative of a larger surface area, for which ground-based ice-penetrating radar data are well-suited. For the three ice rises studied here along the Princess Ragnhild Coast, the ice core records need to be shifted up by 7–15 cm w.e. a$^{-1}$![]() to be representative of the whole ice rise. Without adjustment, they represent the mean SMB state of a maximum of $\sim 200-500$
to be representative of the whole ice rise. Without adjustment, they represent the mean SMB state of a maximum of $\sim 200-500$![]() m radius around the drill site. On the other hand, if the intention is to use ice core records to evaluate the temporal variability of the SMB record, identify the influence of modes of atmospheric variability on SMB (e.g. the Southern Annular Mode, etc), assess models’ representation of SMB temporal variability, there is no need to correct the ice core records. At least for the three ice rises studied here and at the multi-annual to decadal timescale, ice cores seem to adequately track the variability of the SMB signal for the whole ice rise. In summary, our results suggest that, if we need a SMB record that is more representative of the whole ice rise, the ice core SMB record's mean state only requires to be shifted using information from the wider radar surveys, while the temporal variability of the record can be trusted.
m radius around the drill site. On the other hand, if the intention is to use ice core records to evaluate the temporal variability of the SMB record, identify the influence of modes of atmospheric variability on SMB (e.g. the Southern Annular Mode, etc), assess models’ representation of SMB temporal variability, there is no need to correct the ice core records. At least for the three ice rises studied here and at the multi-annual to decadal timescale, ice cores seem to adequately track the variability of the SMB signal for the whole ice rise. In summary, our results suggest that, if we need a SMB record that is more representative of the whole ice rise, the ice core SMB record's mean state only requires to be shifted using information from the wider radar surveys, while the temporal variability of the record can be trusted.
Several ice rises along the Princess Ragnhild Coast have co-located radar data and ice cores records (Matsuoka and others, Reference Matsuoka2015; Goel and others, Reference Goel, Brown and Matsuoka2017, Reference Goel, Martin and Matsuoka2018, Reference Goel2020; Pratap and others, Reference Pratap2021) where it would be interesting to apply our procedure as these ice rises have very similar geographical and therefore glaciological settings. Furthermore, with many more ice core records of SMB available in Antarctica, many with co-located radar surveys, it will be important to test whether the results of this study can be generalized further to the interior of the ice sheet. In particular, it will be important to assess whether the representativeness of pointwise measurements vary with the weather regime or the glaciological regime in Antarctica and therefore with location on the continent. Both in terms of mean SMB and temporal variability of the SMB. If so, this would allow to predict the adjustments that should be applied to ice core SMB records around the continent.
Based on our results, we conclude that there is no ‘ideal’ location for an ice core SMB record as each location on an ice rise records unique conditions that are representative of the surrounding area. We show that what is important is to collect radar surveys that are co-located with the ice core sites. The radar survey should be designed so that it maximizes the spatial coverage of the region of interest and also is dense enough close to the ice core site so that the link between the complementary signals recorded by radar and ice core can be as precise as possible.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/jog.2022.39.
Data availability
The ice cores’ chronology and density data used will be shortly available from S. Wauthy, pers. comm. (2022). The IRH depths and derived SMB are available at https://doi.org/10.14428/DVN/ZLUGD7.
Acknowledgements
We thank Brooke Medley for her code implementation of the Herron–Langway model. This work was supported by the Belgian Research Action through Interdisciplinary Networks (BRAIN-be) from the Belgian Science Policy Office in the framework of the project ‘East Antarctic surface mass balance in the Anthropocene: observations and multi-scale modelling (Mass2Ant)’ (contract no. BR/165/A2/Mass2Ant). Philippe Claeys thanks VUB strategic Research. Hugues Goosse is the research director within the F.R.S.-FNRS. Jan T. M. Lenaerts acknowledges support from the National Aeronautics and Space Administration (NASA), grant 80NSSC18K0201. Marie Cavitte is a Postdoctoral Researcher of the F.R.S-FNRS, Sarah Wauthy is a Research Fellow of the F.R.S.-FNRS. This research contributes to the AntArchitecture action group of SCAR.
Author contributions
M.G.P.C. performed the analysis and wrote the manuscript. H.G. provided analysis and writing support. S.W. provided the ice core chronologies and densities, and edited the manuscript. J.L.T. discussed results and edited the manuscript. T.K. provided method support and edited the manuscript. B.V.L. provided analysis support and edited the manuscript. F.P. collected the radar data and provided processing code. J.T.M.L. edited the manuscript. P.C. provided water stable isotope measurements.