Introduction
The crystal orientation and grain size of polycrystalline ice, also known as 'fabric', is an important feature in the study of glaciers and ice sheets. Orientation, indicated by the direction of the c-axis of a grain, is often used collectively over all grains to interpret the direction of ice flows (Reference AzumaAzuma, 1994), or the thermal history (Reference Landauer and PlumbLandauer and Plumb, 1956) that the crystals have experienced. The typical method of measuring glacier fabric requires that an ice core is drilled and brought to a laboratory, where it is sliced into thin sections and measured using an automated c-axis analyzer (e.g. Reference WilenWilen, 2000; Reference Hansen and WilenHansen and Wilen, 2002; Reference Wilen, Di Prinzio, Alley and AzumaWilen and others, 2003; Reference Wilson, Russell-Head and SimWilson and others, 2003) based on the Rigsby method (Reference RigsbyRigsby, 1951; Reference LangwayLangway, 1958). These analyzers consist of a light source, two polarizers between which the thin slice is oriented, and a camera. A group of four measurements is taken under different sample orientations, from which the directions of the c –axes of the grains in the camera images can be simultaneously obtained. This technique works extremely well, but practical limitations dictate that discrete samples are taken on a recurring depth interval, often every 20 m. This strategy yields a discontinuous record of fabric development.
It is therefore of interest to devise a method to study fabric inside a borehole where a continuous record can be obtained. The transmission method of current analyzers is not compatible with borehole measurements; therefore, a method is proposed using backscattered light, possibly from scattering sites such as bubbles. This could lead to the development of an instrument that could be lowered into a borehole and measure c-axis orientation during its descent.
At pressures that occur naturally near the surface of the Earth, ice crystallizes in a hexagonal structure known as ice Ih (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999). The c-axis of an ice crystal points along the direction of the stacking of the hexagonal layers. The plane perpendicular to this axis is the easy glide plane (Reference Cuffey and PatersonCuffey and Paterson, 2010); therefore, a knowledge of the direction of the c-axis gives a good indication of how stresses have been oriented around a grain over time. Optically, ice is birefringent, with the extraordinary axis corresponding to the c-axis, so optical polarization measurements are a probe of the mechanical condition of the ice.
Methodology
The ordinary (no) and extraordinary (ne ) indices of refraction of ice have the following values at 589 nm (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999):
If a plane wave containing multiple polarization components propagates through the ice, the resulting phase delay or retardance between the two components will be
where λ is the wavelength of the light.
The Jones matrix used to represent this retardation is (Reference Clarke and GraingerClarke and Grainger, 1971)
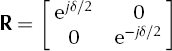
When light is reflected and passes through the ice in the reverse direction, the retardation can simply be represented by the transpose of R due to reciprocity (Reference GoodmanGoodman, 2005). Since R is a symmetric matrix,
The combined effects from the forward and reverse passage of light through the ice are therefore
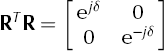
We can therefore treat the reflection as a transmission through the same ice of twice its original thickness.
As illustrated in Figure 1, the c-axis of an ice crystal may be defined by two angles. In the nomenclature of this paper, the Cartesian y-axis will refer to the vertical central axis along a borehole or ice-core cylinder. The x-z plane will refer to the plane perpendicular to this direction. ϕ is the angle in the plane of a hypothetical vertical thin section, and θ is the tilt angle with respect to the surface of the vertical thin section.
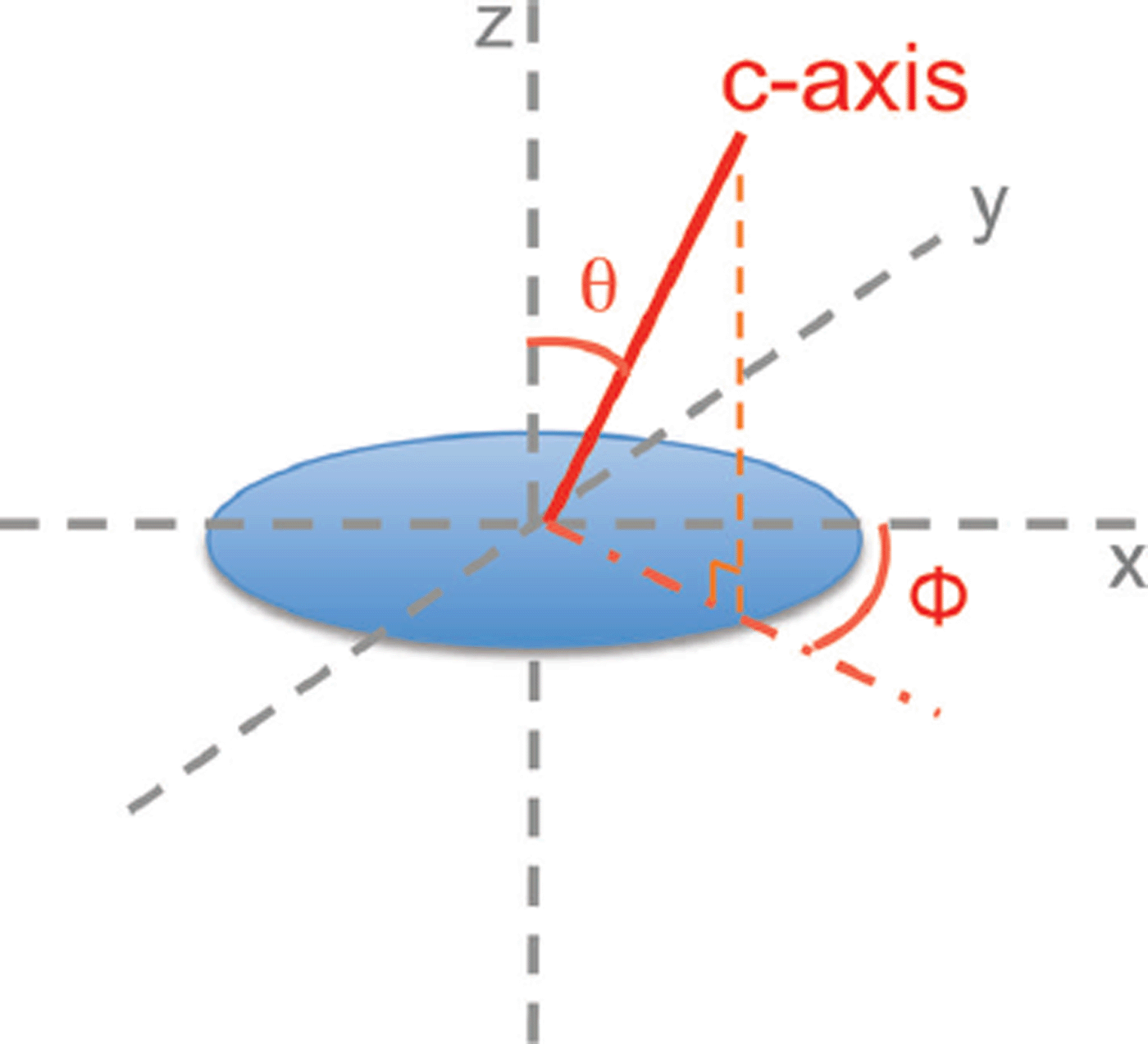
Fig. 1. Defining the c-axis of an ice crystal. The c-axis is in the direction along the stacking of the layers of the hexagonal crystal. The angles θ and ϕ are respectively the azimuth angle and the tilt angle. In this paper, the vertical thin section lies on the x-y plane.
Our reflection-based measurements consisted of four stages: two to determine possible candidates for the two angles, and two to resolve their respective degeneracies. These measurements were conducted inside a chest freezer kept at –34°C on the thin section of ice shown in Figure 2. The thin section was backed with a bare silicon wafer, which acted as a mirror. A collimated fiber-coupled laser source at 675 nm and a silicon detector were used in the four stages of measurements. To ensure that the light source was not polarization-biased, we circularly polarized the beam before it entered the measurement stages, as described in Figure 3. This polarization independence was tested by sending the circular polarized beam through a linear polarizer, which was rotated and the resulting intensity measured by a power meter. No significant intensity changes were seen. The beam splitter used has a ~3°% discrepancy between transmission of s- and p- polarizations, as specified by its manufacturer.

Fig. 2. Image of a vertical thin section from the West Antarctic Ice Sheet (WAIS) Divide ice core from a depth of 420 m. The section is ~250 pm thick. The left side of the image points towards the top of the borehole. The image was taken between a pair of crossed polarizers under white light. The ice crystals are of different colors because of the different extinctions that result from having different c-axis orientations.
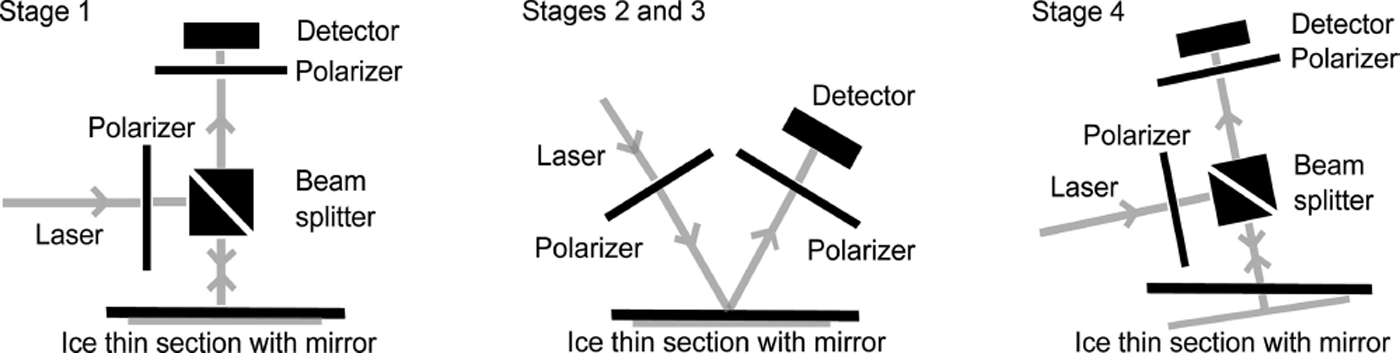
Fig. 3. The four stages of the reflection-based c-axis measurement. Stages 1 and 2 determine ϕ and resolve its degeneracy, while stages 3 and determine θ and resolve its degeneracy. The thin section of ice was backed by a bare polished silicon wafer, which acts as a mirror. During the measurements, the pair of linear polarizers remained crossed at all times.
The ice was placed in the optical path (optically between but not physically between) of two linear polarizers that could be rotated together and were crossed at all times. The measurements utilize the effect of optical extinction. When the axis of the first polarizer aligns with the projection of the c-axis (onto the plane perpendicular to the laser beam) or aligns with a direction in the a-b plane (plane with ordinary index of refraction and perpendicular to the c-axis) then no phase retardance will be imposed on the light since it only experiences one of the refractive indices. As a result, the second polarizer, which is crossed with the first, will not allow light to pass and extinction will be observed. Note in the data that the optical extinction was not perfect, and it is suspected that the roughness of the ice surfaces caused unpolarized optical backscattering.
The procedures for measuring the c-axis of an isolated crystal in the thin section (Fig. 3) are as follows. In stage 1, the light is polarized by the first linear polarizer, passed through the ice crystal and reflected from the ice-silicon interface. The reflected light is then passed through the second polarizer for measurement. The thin section of ice is rotated in-plane from 0° to 90° and stopped at the position where the intensity minimum, or extinction, is found. At this position, the second polarizer axis is aligned with ϕ or ϕ + 90°; in other words, we find ϕ and its degeneracy.
In stage 2, we resolve this degeneracy by keeping the thin section of ice in the minima position and passing the polarized light at an angle of incidence inside the ice of 10°. This angle is chosen because it is far from the Brewster angle, where there are large differences in the reflectivities of the s- and p-polarizations, but it still provides enough projection of the ϕ and ϕ + 90° planes onto the measurement plane to be easily visible in the experiments. The axis of the first polarizer is positioned to be parallel to the thin section of ice. If the extinction remains in the same position, then the true ϕ is indeed the one we found in stage 1. If the position of the extinction shifts, this indicates the true c –axis has a different projection onto the new plane, showing that the true ϕ is in the orthogonal plane, or ϕ + 90°.
In stage 3 we look for θ with the same optical set-up as in stage 2. If the true ϕ is the one we found in stage 1, the thin section of ice is rotated by 90° such that the light is incident and reflected on either side of the vertical plane that contains the c-axis, indicated by the true ϕ. The crossed polarizers are then rotated simultaneously from 0° to 90°. Extinction occurs at an angle α, which forms a plane with the propagation direction ' that contains the c-axis. Intersecting with the plane we conclude from stage 2, we find θ or θ + 90°; in other words, we find θ and its degeneracy.
Mathematically, using the notations in Figure 4, we find plane 1 from stage 2 and it can be represented by its normal
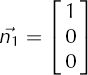
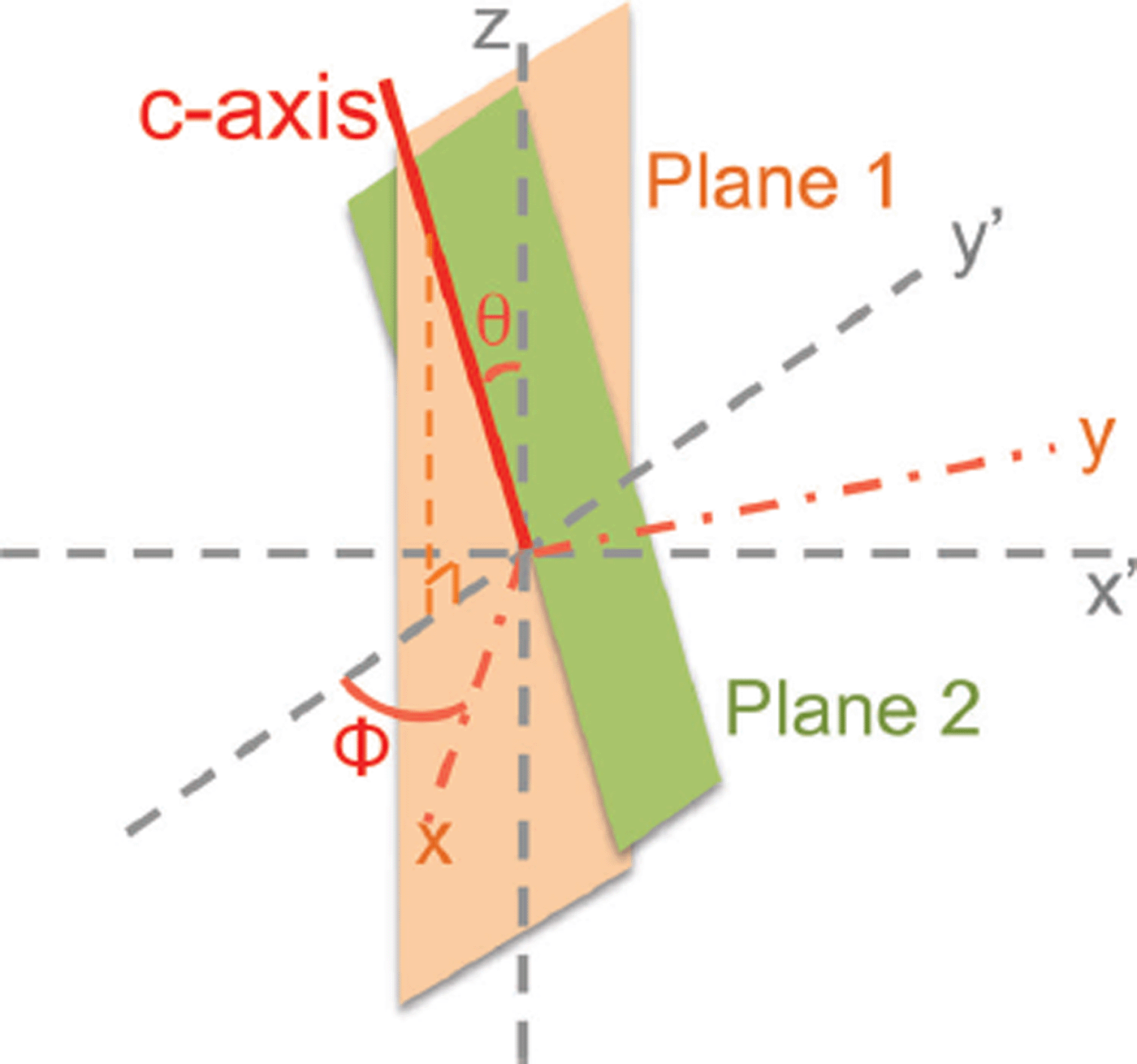
Fig. 4. Intersection of planes in stage 3. In stage 3, the thin section of ice is rotated to a x′-y′ frame such that the plane found in stage 2 is oriented to the y′-z′ plane, indicated by plane 1 in orange, and the light is incident at an angle β from the z-axis in the x′-z plane. Extinction occurs at a polarizer angle α, and that forms a plane with the light propagation direction, indicated by plane 2 in green. Planes 1 and 2 intersect at the c-axis or its degeneracy.
Now, in stage 3, the measurement does not occur normal to the y-z plane, but rather at an angle β to the normal (inside the ice). This means that the relevant light propagates at an angle β inside the ice from the z-axis in the x’-z plane. In our experiment, β is at 10°. This light propagation vector could be represented by
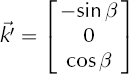
The polarizers are rotated and extinction occurs at angle α at the first polarizer. To find this vector mathematically, we first define a vector ![]() on a polarizer that is parallel to the x-y plane as illustrated in Figure 5:
on a polarizer that is parallel to the x-y plane as illustrated in Figure 5:
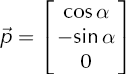
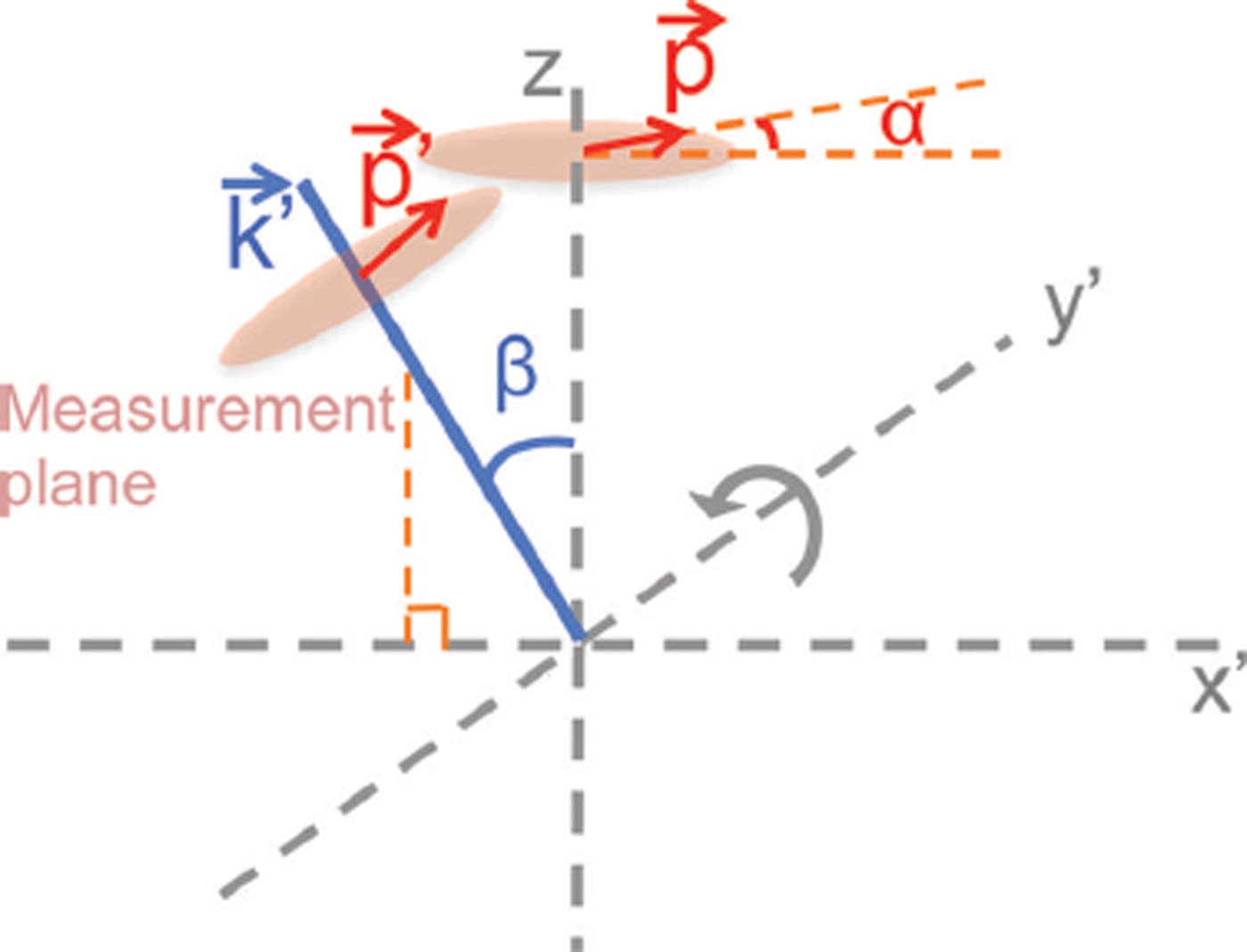
Fig. 5. Defining the polarizer extinction direction vector ![]() in stage 3. Light is incident at an angle β from the z-axis on the x′-z plane, as described by the propagation vector
in stage 3. Light is incident at an angle β from the z-axis on the x′-z plane, as described by the propagation vector ![]() . Extinction occurs at an angle α on the polarizer measurement plane, which is also tilted at β and is perpendicular to
. Extinction occurs at an angle α on the polarizer measurement plane, which is also tilted at β and is perpendicular to ![]() . Mathematically we can define a vector
. Mathematically we can define a vector ![]() , which is parallel to the x′-y′ plane. We can then tilt it by β around the y′-axis using a rotation matrix.
, which is parallel to the x′-y′ plane. We can then tilt it by β around the y′-axis using a rotation matrix. ![]() , a vector on the measurement plane at which extinction occurs, results.
, a vector on the measurement plane at which extinction occurs, results.
To obtain the direction in the measurement plane, which is tilted by β relative to the x-y plane, we perform the rotation
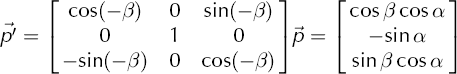
where ![]() is perpendicular to
is perpendicular to ![]() , and
, and ![]() represents the direction on the measurement plane at which extinction occurs.
represents the direction on the measurement plane at which extinction occurs.
The plane 2 that they form can be represented by the normal
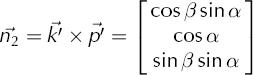
The two planes intersect at the c-axis, which can be found by
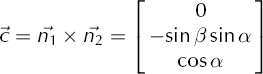
Therefore we can find θ with
In stage 4, the mirror is tilted and the laser and detector are aligned such that we have a direct back-reflection from the mirror. We approximate θ to be α at the time of measurement. The tilting angle is adjusted according to Snell's law, such that the light path in the ice is at the angle a, found in stage 3, to the vertical z-axis. The polarizers are rotated simultaneously. If extinction remains, the true c-axis is estimated to be closer to the light path and the true θ is the θ that we found in stage 3. Otherwise the true θ is in the orthogonal plane, or θ + 90°.
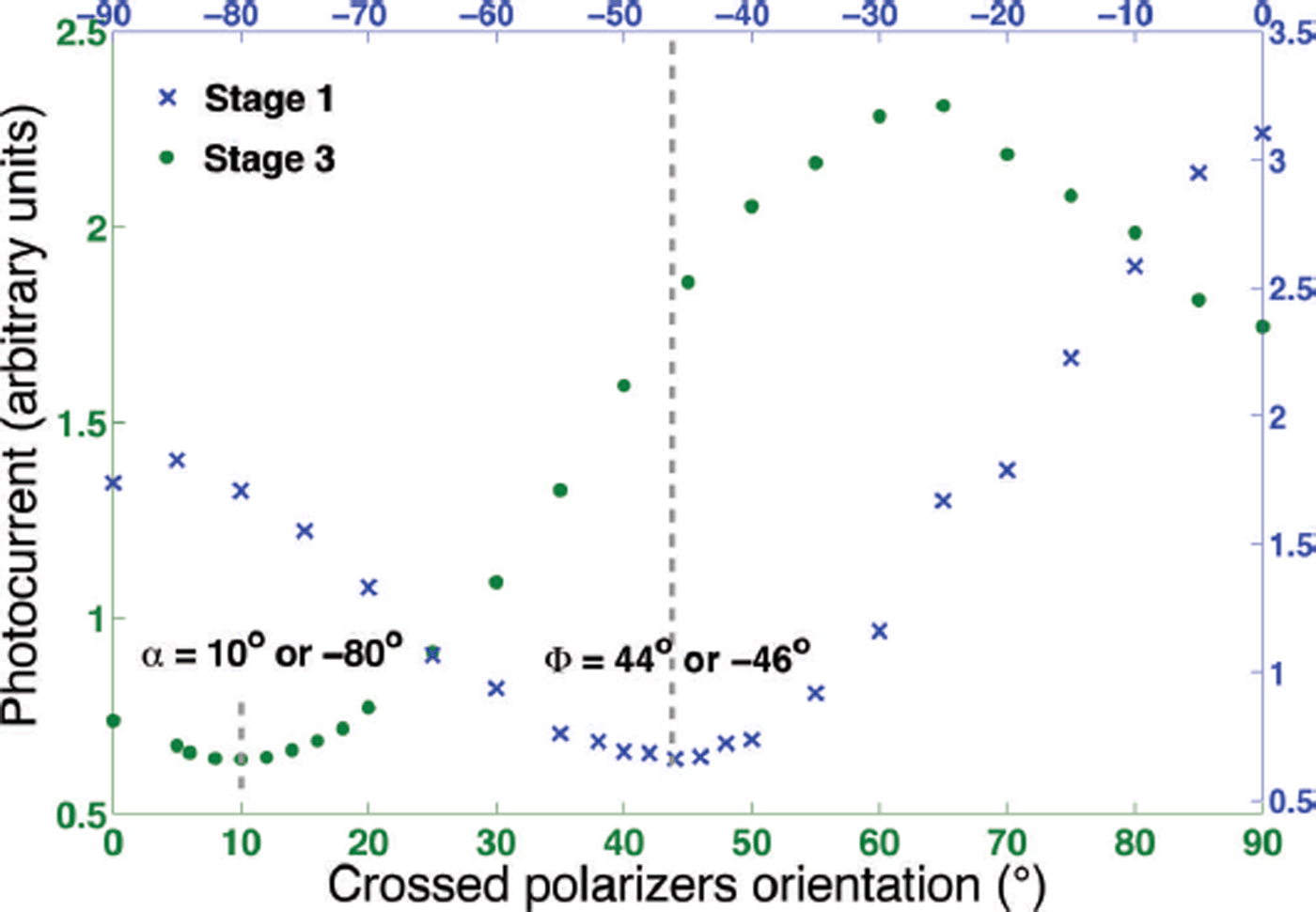
Fig. 6. Measurement results from stages 1 (blue crosses) and 3 (green dots) on crystal 11. The minima on the two curves indicate the angles ϕ and α or their degeneracies. Stages 2 and 4 are single point measurements to determine whether the intensity is no longer at a minimum, and are not shown in this graph.
Results
Eleven easily visible crystals were chosen across the thin section and their c-axes were measured. Figure 6 shows the measurements from stages 1 (blue curve) and 3 (green curve) on crystal 11. The angles at which intensity minima, or extinction, occurred are the ϕ and α of the crystal or their degeneracies. Stages 2 and 4 (not shown) were single point measurements to determine whether the reflected light was out of extinction. The resolution of the measurements is estimated to be ±1°, limited by the precision of a manually rotated polarizer. Table 1 summarizes the results from 11 crystals, including that illustrated in Figure 6. The measured results were mostly in line with data from a transmission-based automated fabric analyzer (indicated by asterisks in Table 1; Reference Wilen, Di Prinzio, Alley and AzumaWilen and others, 2003), with the exception of crystal 7.
Table 1. Results of the reflection method for the 11 crystals in comparison with results using an automated fabric analyzer (indicated by asterisks). Stage 1 found the two possible ϕ, and stage 2 eliminated one of them. Stage 3 found the two possible θ, and stage 4 eliminated one of them. All values, including errors, are in degrees
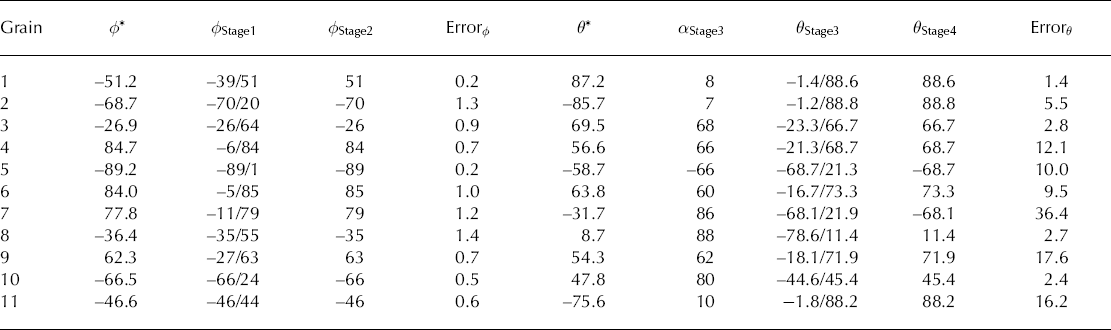
It is found that measurements of the crystal orientations (ϕ, θ) in 11 grains showed an average error of ±0.8° in ϕ, with no grain error >1.4°. Measurements of θ showed an average error of ±8. 2° on 10 of the 11 grains. The measurement on grain 7 showed exceptional error with determination of θ. We are uncertain of the origin of the error on this particular grain.
Future Work
This proposed reflection-based c –axis measurement method is a first step towards a continuous method to study ice crystal orientations in situ in a borehole. A critical next step is the adaptation of the technique to measurements of bulk ice using bubbles and other backscatterers instead of mirrors as reflectors. To demonstrate the possibility of such atechnique, a backscattering measurement was carried out at the US National Ice Core Laboratory. A HeNe laser beam was incident through a linear polarizer upon an ice core GISP2D MCA1 (435.25–436.00), and the backscattering was measured using a silicon photodetector through another polarizer that was crossed to the first one. As the pair of crossed polarizers rotated together, the backscattering measured showed a generally sinusoidal shape and a clear minimum (Fig. 7), serving as a proof of concept for polarization measurements using backscattering in bulk ice. Note that the polarization signals were clearly visible despite confounding factors such as the roughness of the surface, surface reflection and microcracking around the bubbles that has taken place over the two decades since the ice core was extracted.
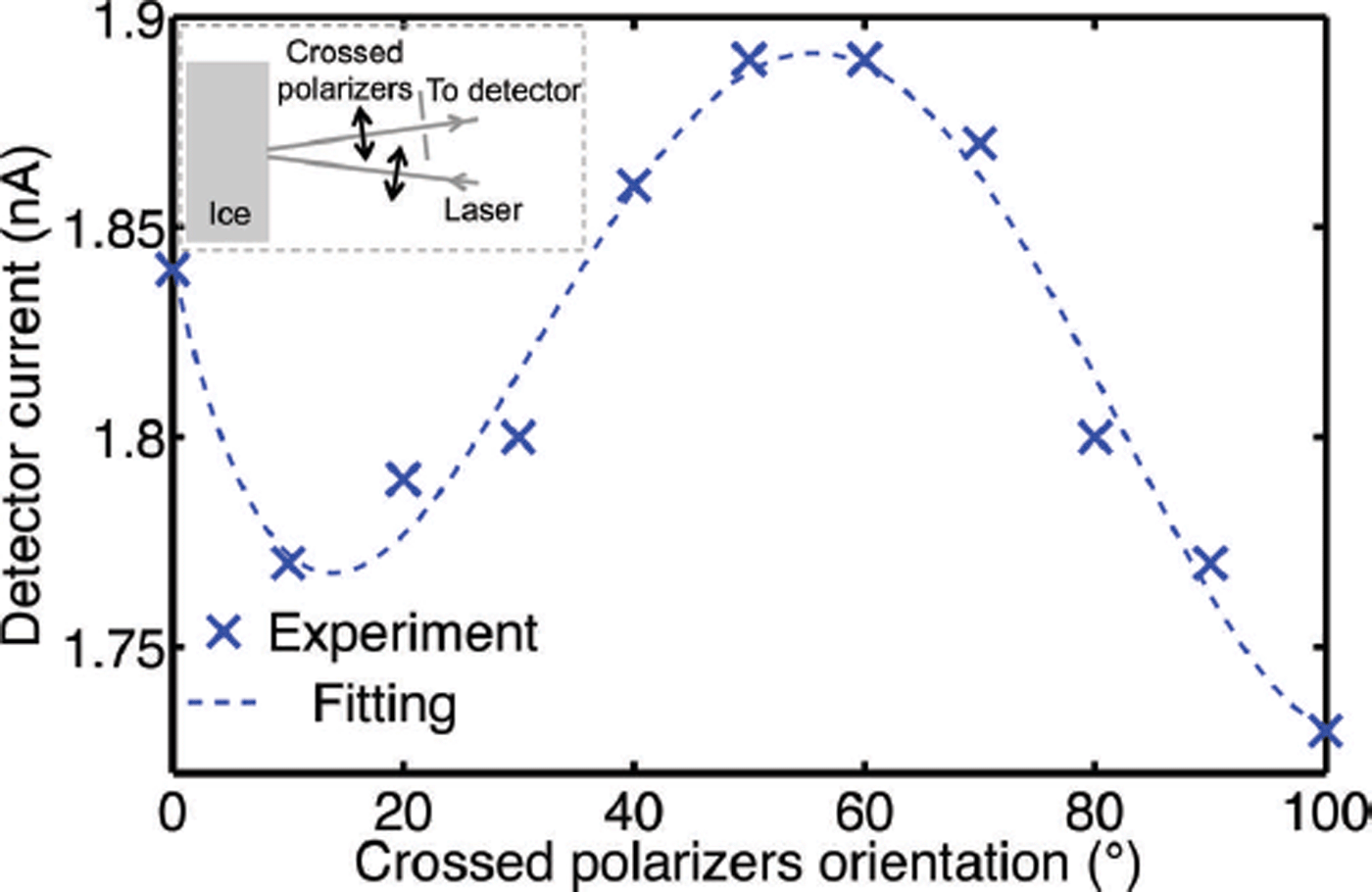
Fig. 7. Backscattering measurement results through a pair of crossed polarizers on GISP2D MCA1 (435.25–436.00). The ice was 35 mm thick at the measurement spot. As the pair of polarizers rotated together, the backscattering intensity reached a clear minimum, showing the polarization dependence of the bulk ice. The inset illustrates the optical set-up of the experiment.
Acknowledgement
This work is supported by US National Science Foundation Antarctic Sciences grant 1142010 under Julie Palais.












