1. Introduction
The Antarctic Peninsula (AP) region has experienced rapid climate warming in recent decades (Reference VaughanVaughan and others, 2003; Reference TurnerTurner and others, 2005), with a variety of related glacier responses including retreat of marine fronts (Reference Cook, Fox, Vaughan and FerrignoCook and others, 2005), acceleration of flow (Reference Pritchard and VaughanPritchard and Vaughan, 2007), increased melt season duration (Reference VaughanVaughan, 2006; Reference BarrandBarrand and others, 2013) and retreat and collapse of fringing ice shelves (e.g. Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000; Reference Van den BroekeVan den Broeke, 2005; Reference Cook and VaughanCook and Vaughan, 2010). These shelf collapses have resulted in accelerated inland ice flow (e.g. Reference De Angelis and SkvarcaDe Angelis and Skvarca, 2003; Reference Rignot, Casassa, Gogineni, Krabill, Rivera and ThomasRignot and others, 2004; Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011) and subsequently increased contribution to sea-level rise (Reference RignotRignot and others, 2008; Reference Shuman, Berthier and ScambosShuman and others, 2011). Regional-scale estimates suggest substantial contributions to sea-level rise from the surface mass balance of peripheral glaciers and ice caps (including islands adjacent to the mainland AP) (Reference Hock, De Woul, Radić and DyurgerovHock and others, 2009) and from mass losses including the mainland AP ice sheet (Reference RignotRignot and others, 2008; Reference Ivins, Watkins, Yuan, Dietrich, Casassa and RülkeIvins and others, 2011; Reference ShepherdShepherd and others, 2012).
The large volume of ice contained within the AP, combined with high sensitivity to climate warming (Reference Hock, De Woul, Radić and DyurgerovHock and others, 2009) and the potential for further ice-shelf collapse (Reference Vaughan and DoakeVaughan and Doake, 1996; Reference Morris, Vaughan, Domack, Leventer, Burnett, Bindschadler, Convey and KirbyMorris and Vaughan, 2003) and subsequent sustained outlet glacier acceleration (Reference Berthier, Scambos and ShumanBerthier and others, 2012) imply that future ice loss from the AP region may be substantial. Projections of volume change from surface melt of glaciers peripheral to the Antarctic continent (i.e. sub-Antarctic islands and islands of the AP), using temperature and precipitation scenarios from a range of global climate models, suggest an addition of 5–40 mm to global sea levels by the end of the 21 st century, a contribution similar to that expected from surface mass loss of glaciers in Alaska or the Canadian Arctic Archipelago (Reference Radić and HockRadić and Hock, 2011). These estimates, however, do not include the contribution to sea level from changes of the much larger Antarctic Peninsula ice sheet (APIS), nor changes in ice flux due to grounding-line retreat of tidewater and shelf-terminating glaciers, changes in accumulation, and accelerated flow following ice-shelf removal. The interplay of these dynamic forcings is likely to substantially alter the volumetric response of the AP to future climate warming and thus its total contribution to sea level. Accurate projections from the AP require models that include the larger grounded ice sheet and are capable of simulating such changes in glacier dynamics.
This study develops and applies a new dynamical scheme for projecting the volume response of the APIS to future climate warming. A new ice-sheet model framework for the AP is presented, followed by results of model simulations applied to the entire ice sheet with forcing from distributed surface mass-balance projections, and imposed changes to the 20 largest outlet glaciers in Palmer Land, southern AP (excluding Drewry–Evans Ice Stream; Fig. 1). The model is initialized with surface velocities from interferometric synthetic aperture radar (InSAR) remote sensing, a new ice surface elevation model, and surface mass-balance fields from output of the regional atmospheric climate model RACMO2. Volume projections to 2200 were calculated using annual surface mass-balance fields forced by emissions scenario outputs of two global atmosphere–ocean general circulation models, and imposed grounding-line retreat and ice-shelf break-up scenarios at selected outlet glaciers. In the absence of accurate ice thickness data and precise predictions of the timing of shelf break-up, this scenario-based approach is used to generate a range of glaciologically plausible estimates of the potential contribution to sea level from the APIS during the coming two centuries.

Fig. 1. Location map of the Antarctic Peninsula ice sheet showing drainage basins and major ice-shelf systems (labelled in italic text). Model simulations were run over the entire grounded portion of the ice sheet and outlet glaciers with perturbation from AP-wide distributed surface mass-balance projections, and imposed grounding-line retreat and ice-shelf removal at the 20 selected drainage basins in Palmer Land. Drainage basins were delineated using surface hydrological tools in the ArcGIS software package. The 20 largest basins (in Palmer Land) are labelled by size rank (1 is the largest) and shaded dark grey. Thick white lines are plotted between the position of the present-day (2000s) grounding-line and a position 20 km upstream along the main flowline.
2. Geographical setting and Data Sources
The Antarctic Peninsula is a glaciated mountain chain stretching ∼1300 km between Ellsworth Land in West Antarctica and the Trinity Peninsula at the northern limit of Graham Land (Fig. 1). It comprises the narrow central spine of Graham Land (63–69° S) and the wider, higher Palmer Land (69–75° S) (Fig. 1). Our definition of the APIS excludes peripheral glaciers and ice caps on islands adjacent to the peninsula and is limited to the grounded, mainland AP (Fig. 1). The ice sheet originates at elevation in the interior, with ice flowing through drainage basins (Fig. 1) predominantly towards tidewater-terminating glacier fronts in Graham Land and into ice shelves throughout Palmer Land. The main exceptions in Graham Land are the glaciers on the east coast flowing into the remnant Larsen B and Larsen C ice shelves. Examples of tidewater- and shelf-terminating glacier fronts typical of the AP are shown in Figure 2. With its larger area and thicker ice, the bulk of AP ice is contained within Palmer Land. This region contains the 20 largest drainage basins, which together comprise ∼40% (111 704 km2) of the total ice-covered area of the grounded mainland section of the AP (289 264 km2 not including the Drewry–Evans Ice Stream catchment draining the southern part of Palmer Land into the Ronne Ice Shelf) (Fig. 1). While ice thickness of AP outlet glaciers is still relatively poorly known, existing measurements indicate that bedrock topography is not substantially overdeepened upstream of the grounding line (Fig. 3b), thus making marine ice-sheet-like instability unlikely. This means that the expected retreat of AP outlet glaciers is not analogous to that of other glaciers of West Antarctica (e.g. Pine Island Glacier).

Fig. 2. Illustration of tidewater- and shelf-terminating outlet glaciers on the AP: (a) calving front and lower reaches of tidewater Erskine Glacier, terminating into Darbel Bay (66.5° S, 65.6° W); and (b) Clifford Glacier (70.4° S, 62.5° W), flowing into Smith Inlet of the Larsen D ice shelf. Imagery is from the Landsat Image Mosaic of Antarctica (LIMA, http://lima.usgs.gov/). Surface velocities in the upper panels are from InSAR observations (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011).

Fig. 3. Physical glaciology of the AP: (a) ice surface elevation of the grounded ice sheet including major drainage basin divides; (b) bedrock topography of the AP and surroundings from Bedmap2 (Reference FretwellFretwell and others, 2013); (c) ice surface velocity from InSAR remote sensing (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011; gaps in the ice-cap interior were filled using calculated balance velocities); and (d) accumulation from output of the regional climate model RACMO2 (Reference Ligtenberg, Van de Berg, Van den Broeke, Rae and Van MeijgaardLigtenberg and others, in press).
Information required for modelling the flow of the APIS includes ice-surface elevation, ice thickness, velocity and the surface mass-balance rate. Surface elevation data were provided by creating a new 1 km post-spacing digital elevation model (DEM) using satellite altimetric and photogrammetric datasets (Fig. 3a). The DEM was constructed by combining a satellite radar and laser altimetry model of Palmer Land (south of 69° S) (Reference Bamber, Gomez-Dans and GriggsBamber and others, 2009) with a mosaic of seven resampled SPOT5-HRS stereophotogrammetric DEMs (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009) and more than 70 tiles from version 2 of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global DEM (www.gdem.aster.ersdac.or.jp/), throughout Graham Land and at low elevations within Palmer Land. The DEM was resampled to the resolution of the ice model (900 m) and cropped to the grounding line of the MODIS Mosaic of Antarctica (MOA; Reference Haran, Bohlander, Scambos, Painter and FahnestockHaran and others, 2006), and bedrock pixels were identified and excluded using a resampled polygon shapefile from the Antarctic Digital Database (www.add.scar.org/).
Bedrock topography and ice thickness grids were obtained from the Bedmap2 compilation (Reference FretwellFretwell and others, 2013; Fig. 3b). Despite considerable improvements in the quality and coverage of continental Antarctic bed elevation data in Bedmap2, large data gaps still persist throughout the APIS (especially for outlet glaciers). The consequences of these limited ice thickness data are to an extent mitigated, however, by our ice-sheet model initialization and linearized method (Section 3). Ice surface velocities were compiled from a mosaic of Antarctic ice motion data from multiple InSAR scenes acquired during 2007–09 (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011; Fig. 3c). Surface mass-balance fields used to initialize the model prior to 1999 and to run projection simulations to 2200 were obtained from output from RACMO2 (Reference Van MeijgaardVan Meijgaard and others, 2008; Reference Ligtenberg, Van de Berg, Van den Broeke, Rae and Van MeijgaardLigtenberg and others, in press) (e.g. Fig. 3d). Initialization fields were obtained from RACMO2 simulations of annual surface mass balance between 1980 and 1999, forced by data from the European Centre for Medium-Range Weather Forecasts ERA-40 reanalysis (Reference UppalaUppala and others, 2005). Future projections used RACMO2 annual surface mass-balance grids using a variety of forcings. The regional model was run using lateral boundary conditions from two global climate models: ECHAM5 (www.mpimet.mpg.de/en/wissenschaft/modelle/ echam) and the Hadley Centre Coupled Model, version 3 (HadCM3). Both global models were run using Intergovernmental Panel on Climate Change (IPCC) global emission scenarios A1B and E1, respectively corresponding to middle-of-the-road and aggressive mitigation emissions scenarios. These boundary conditions provided a total of four scenarios of projected surface mass balance to 2200 (Reference Ligtenberg, Van de Berg, Van den Broeke, Rae and Van MeijgaardLigtenberg and others, in press). While HadCM3 was run from 2000 to 2199, ECHAM5 was run only between 2000 and 2099, therefore 2100–99 ECHAM5 fields consist of the 2090–99 grids repeated ten times.
3. Model Description and Experimental Approach
3.1. Overview
Marine-terminating outlet glaciers such as those draining the APIS change mass either by changes in ice flux, changes in surface mass balance or changes in the position of the grounding line. To model these changes, one needs a sufficiently accurate initial description of the ice sheet. The initialization procedure we use, which focuses on accurate representation of ice velocity and the rate of surface elevation change, is described below, while the meteorological model experiments have been outlined above. Our model experiments consist of forcing an initialized model of the entire grounded mainland APIS with distributed surface mass-balance anomalies, and with both imposed perturbations of the grounding line at selected outlet glaciers in southern Palmer Land (Fig. 1) and instantaneous removal of ice shelves fringing these outlets. The model description and approach to these experiments are detailed below.
Grounding-line migration is expected at AP outlet glaciers as a consequence of further ice-shelf collapse. Such collapse reduces buttressing forces across the grounding line, leading to retreat. Reference SchoofSchoof (2007) showed that flux across the grounding line is proportional to ice thickness and back-pressure to some high powers. Back-pressure arises from the presence of ice shelves and is particularly affected by melting adjacent to the grounding line (Reference Goldberg, Little, Sergienko, Gnanadesikan, Hallberg and OppenheimerGoldberg and others, 2012a,Reference Goldberg, Little, Sergienko, Gnanadesikan, Hallberg and Oppenheimerb). Moreover, the processes leading to and governing the timing of ice-shelf collapse are very poorly understood. Oceanographic conditions under AP ice shelves are essentially unknown, but a more fundamental problem is poor knowledge of the bedrock topography of those outlet glaciers that are expected to retreat. Without this knowledge, the analysis of Reference SchoofSchoof (2007) shows that process-based approaches to modelling grounding-line retreat will be beset by significant errors at every step.
Very rapid forcing of grounded ice by removal of shelf ice has recently been analysed by Reference Williams, Hindmarsh and ArthernWilliams and others (2012). They show how to compute a time-span over which membrane stresses (horizontal stress gradients; e.g. Reference HindmarshHind-marsh, 2006), which we ignore, are important. This analysis, applied to our 20 drainage basins in Palmer Land (see Fig. 1), showed that the period is roughly decadal (mean of 22.6 years; Table 1). Forecasts over the early decades following break-up, therefore, will be subject to errors arising from ignoring membrane stresses. Over longer periods, however, corresponding to our forecast scenarios, these errors will decay. Table 1 shows the important physiographic attributes of the 20 largest drainage basins in Palmer Land, as well as the theoretical maximum velocities for an unbuttressed frictionless ice stream, using flotation thicknesses at the estimated grounding line position. These velocities can be much larger than observed velocities, but in some cases are less than observed values. We attribute this to errors in the thickness of the grounding line, most likely due to mislocation of the grounding line position. The variability of these numbers shows how critical obtaining good bed topography is for modelling the time-dependent grounding-line retreat. At the moment, these data are not available, and this serves as a rationale for an approach of imposing grounding-line retreat. Very large positive differences are indicative of the possibility of grounding-line retreat; a simple continuity argument implies that retreat rates are of the same order of magnitude as the velocity difference, potentially several kilometres a year.
Table 1. Physiographic characteristics and frequency response of 20 selected glaciers in Palmer Land, southern AP. Velocities [u*] are from Reference Rignot, Mouginot and ScheuchlRignot and others (2011), and ice thickness [H*] was calculated from measured grounding-line surface elevations [s*] using [H*] = [s
*]/(1 – ρ
i/ρ
w), where ρ
i is the density of ice and ρ
w the density of sea water. ![]() is a measure of the demarcation between the fast and slow forcing branches of the frequency response and gives an estimate of the timescale of forcing below which membrane stresses are important. For details of this approach see Reference Williams, Hindmarsh and ArthernWilliams and others (2012). Following Reference HindmarshHindmarsh (2012), we calculate
is a measure of the demarcation between the fast and slow forcing branches of the frequency response and gives an estimate of the timescale of forcing below which membrane stresses are important. For details of this approach see Reference Williams, Hindmarsh and ArthernWilliams and others (2012). Following Reference HindmarshHindmarsh (2012), we calculate ![]() , the velocity of each ice stream if it were perfectly slippery and unbuttressed, which thus gives an estimate of the maximum velocity.
, the velocity of each ice stream if it were perfectly slippery and unbuttressed, which thus gives an estimate of the maximum velocity. ![]() is the difference between this maximum velocity
is the difference between this maximum velocity ![]() and the measured velocity [u*]. Average values for all 20 basins are also shown
and the measured velocity [u*]. Average values for all 20 basins are also shown

In view of these uncertainties, we did not attempt to model grounding-line retreat explicitly, but chose instead to investigate the consequences for the APIS of imposing instantaneous grounding-line retreat at each of the 20 chosen basins. We imposed retreats of 10 and 20 km from the present-day grounding-line position of these basins (see Fig. 1) and investigated the volumetric response of the entire APIS to these retreats. In summary, our modelling approach consists of a geographically realistic representation of current flow of the APIS, but with less realistic representations of the changes in this flow arising from changes in the forcing and boundary conditions. Preliminary experiments showed that a procedure targeted at understanding likely maximum responses delivered useful information, in the sense that total deglaciation of the AP is essentially impossible over two centuries, but they also showed that total ice loss is potentially a significant proportion of total ice volume.
3.2 Approach to initialization
Ice models operate in two manners. Given a geometry, they operate diagnostically, and compute the instantaneous velocity field. They can also operate prognostically, using their calculation of velocity fields, together with surface mass balance, to calculate changes in the geometry. For their input, the models require ice surface elevation, bed elevation, surface mass-balance rates, as well as a description of the way the ice deforms (ice rheological parameters) and the way it slides over the bed (sliding parameters), which we lump together as the deformation parameters. While laboratory experiments can constrain the ice rheology to some extent, it is necessary to invert for the sliding parameters in order to initialize an ice-sheet model in such a way that it can be run prognostically.
There are two approaches to initialization: velocity initialization techniques (VIT) focus on matching observed velocities (e.g. Reference MacAyealMacAyeal, 1992; Reference Vieli and PayneVieli and Payne, 2003; Reference Joughin, MacAyeal and TulaczykJoughin and others, 2004; Reference Morlighem, Rignot, Seroussi, Larour, Ben Dhia and AubryMorlighem and others, 2010), while altimetric initialization techniques (AIT) focus on matching rates of change of elevation of the ice surface (Reference HindmarshHindmarsh, 1997; Reference Arthern and HindmarshArthern and Hindmarsh, 2003; Reference Morlighem, Rignot, Seroussi, Larour, Ben Dhia and AubryMorlighem and others, 2011). The computation of balance velocities can be viewed as an altimetric initialization technique. In a more formal sense we seek to minimise a cost function J that we may write as
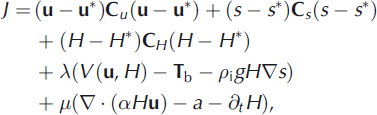
where u and u* are the modelled and observed surface velocities, H and H* are the modelled and observed ice thicknesses, s and s* are the modelled and observed surface elevations, C u , C H and C s are weighting matrices reflecting the error in the observations, ρ i is the density of ice, g the acceleration due to gravity, T b the basal drag, V(u, H) represents the internal viscous forces, α is the ratio of mean velocity to surface velocity and a is the surface mass-balance rate. The quantity of the constant α is not known, and depends on the internal viscous flow engendered by the driving stress and the geometry. This equation represents an attempt to simultaneously seek a best fit to the observed momentum balance (V (u, H) – T b – ρ i gH∇s) and mass conservation (∇ · (αH u) – a – ∂tH) equations. These are constrained respectively by the Lagrange multipliers A and p.
In a full mechanical description, V(u, H) symbolizes the operation of the resistive forces in the Stokes equations. In practice, one would use an approximate mechanical model, symbolized by M(u, H) = V(u, H) + Eλ , where Eλ is an error term. One can also fold in the errors in the unknown H into Eλ: By using this model, one also introduces errors into α, to represent which we write the continuity equation as ∇ · (αMH u) – a + Eμ , where αM denotes the α obtained through using the mechanical model M, and Eμ. is the error arising from αM: Taking into account the model errors, the cost function is written
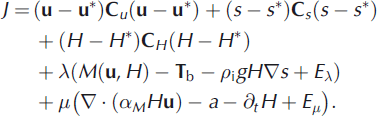
It is clear that the usefulness of the procedure to obtain good estimates for u, s and H with this formalism depends on whether the error terms Eλ and Eμ. are small.
The above formalism, while comprehensive, has never been applied to an ice sheet. The most widely used version is a VIT originally due to Reference MacAyealMacAyeal (1992), and extensively applied by Reference Joughin, MacAyeal and TulaczykJoughin and others (2004). In ice streams, the ice thickness is relatively uniform, meaning that interpolation onto computational grids is an accurate procedure and the surface slopes are small, allowing satellite altimeters to measure surface elevations accurately. The membrane stress approximation appears to be a good mechanical model in ice streams, allowing us to set αM = 1 (Reference MacAyealMacAyeal, 1992). The mass conservation constraint is not used by Reference Joughin, MacAyeal and TulaczykJoughin and others (2004), meaning that in principle their optimal solution for the velocity might give erroneous ∂t H, although in practice this seems not to be the case.
The conditions that allow successful inversions for the sliding parameters on ice streams do not seem to apply to the complex topography of the AP, and in consequence we propose a combined altimetric and velocity initialization. The basic motivation is that the ice thickness is very poorly known, and while it is clear that the rugged basal topography implies the necessity of using sophisticated full-Stokes models (see, e.g., Reference Hindmarsh, Leysinger Vieli, Raymond and GudmundssonHindmarsh and others, 2006) the absence of accurate thickness data renders it pointless to use them, even if it were computationally practicable. In consequence, we eliminate the mechanical model from the initialization, focusing on mass conservation. This has the consequence that there is no requirement to include the surface topography s in the cost function. The absence of a reliable mechanical description also implies that we cannot estimate αM reliably, meaning that we cannot expect to be able to use mass conservation to interpolate ice thickness. Further difficulties in this approach are discussed by Reference SeroussiSeroussi and others (2011). In view of this, we arrive at the trivial cost function
where Heff = αH is the effective thickness. It is possible to solve uniquely for the effective thickness, meaning that one can use topologically admissible velocity fields directly, to write the equation
to solve for the effective thickness. Topologically admissible ice-sheet velocity fields exclude sinks and helical (rotatory) flows unless there is highly localized ablation. In our forecasting approach, we do not require the effective thickness, but only the flux q = H eff u*.
We adopt this approach, since recently a substantial proportion of the Antarctic ice velocity fields have been mapped (Reference Rignot, Mouginot and ScheuchlRignot and others, 2011). These are used to define u* where available. In regions where they are not available, balance fluxes are used to estimate the fluxes. The caveat of topologically admissible fields has some practical importance, as at a small number of locations (fewer than 100) such fields were found during initialization. We were faced with the choice of developing an inverse method which removed them, or adjusting the data. In either case, an approximation to the data is used in the model. We chose the latter, because the sinks are, by definition, areas where both velocity components change sign, and therefore occur where velocities are low. Many of these locations occurred in the domes of the small peninsulas that comprise much of the coastline of the northern AP. Where necessary, the adjustment procedure consisted of changing the signs of the velocity in the immediate areas of the sink, so as to eliminate the sink (topologically, we cause the sink and a nearby saddle to annihilate). Helical flows corresponded to zones of overall convergence a few kilometres in span that did not include sinks, and were eliminated by similar means.
A further problem with the data was the misalignment of the directions of maximum slope and velocity. This is of course feasible in principle owing to complex mechanical effects, but can lead the simplified model to violate the second law of thermodynamics. This problem occurred mainly in slow-flowing areas; in the outlet glaciers slope and velocity vectors were nearly parallel. The maximum glaciodynamical response occurs when the two vectors are aligned. Thus, in keeping with our interest in seeking the maximum response, we computed base-case zeroth-order absolute slopes (see Section 3.3 for how these are used) and then aligned the slope components with the observed velocity vectors.
To forecast we use a method that builds from the AIT proposed by Reference HindmarshHindmarsh (1997). In its original form, it computed balance velocities and balance fluxes, and computed a linearized operator to investigate small ice thickness changes, small being defined as a proportion of the ice thickness or surface slope. This approach has the signal advantage of not requiring an explicit estimate of the deformation parameters, as their influence is automatically included, as explained below. In most parts of the AP, changes in ice thickness due to changes in surface mass balance over 200 years are expected to be small in this sense. This is not the case for changes caused by grounding-line retreat. As will be seen, the major contribution to sea level is the extent to which grounding-line retreat causes upstream thinning, timescales for which are determined by velocities. Our altimetric and velocity-based initialization ensures that this aspect is estimated well.
3.3. Mathematical basis
3.3.1. Zeroth-order flux computation consistent with finite-difference grids
Given that the perturbation procedure (imposed retreat of the grounding line) will be carried out on a finite-difference grid, it is highly desirable that the zeroth-order fluxes satisfy the conservation equation exactly. The procedure is simply to compute the flux arriving at a gridpoint from x- and y-direction connections, compute the flux out using continuity and divide it between all the outlet connections in linear proportion to their velocity. Then, q = H u: A finite-difference approximation is
for each of the outlet points, where H i , j is an unknown. We can solve for the outlet discharges and H eff, i, j with the additional equation
In practice, we compute for the grid-centred fluxes by solving a set of linear equations, in ∼320 000 unknowns (corresponding to a close approximation of the total number of points considered), which results in a sparse matrix of this size. Topologically inadmissible fields give rise to a singular matrix; the locations of these may be obtained by computing the null space of the matrix using the method of Reference Higham and TisseurHigham and Tisseur (2000), and eliminated using the procedure described above.
3.3.2. The ice-sheet equation and its linearizations
When considering the mechanics of ice sheets, we use a reduced model (Reference HutterHutter, 1983; Reference MorlandMorland, 1984; Reference FowlerFowler, 1992) obtained from a scaling of the Stokes equations. The scaling yields simple functional forms for the vertical variation of the stress field and a considerable computational saving. Further manipulation of the reduced model results in the ice-sheet equation
where H, s and a (defined following Eqn (1)) are functions of x, y and t, and where C, m and v are explained below. Boundary conditions for this model are
where y = Y(x) is the prescribed margin.
The evolution equation (7) describes the evolution of ice-sheet thickness where the flow mechanism is either internal deformation according to some nonlinearly viscous flow law or sliding according to some Weertman-type law. The analyses we shall carry out are not in principle limited to these situations. For internal deformation, the quantity C is directly related to a weighted vertical average rate factor ![]() (defined below in Eqn (13)) of the rate factor Ad
used in the viscous relationship
(defined below in Eqn (13)) of the rate factor Ad
used in the viscous relationship
where E is a second invariant of the deformation rate and τ is a second invariant of the deviator stress (Reference GlenGlen, 1955). For basal sliding, C comes from a sliding relation of the form
(Reference WeertmanWeertman, 1957). We construct the following quantities for use in the general evolution equation:
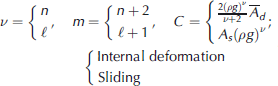
The derivation of the evolution equation (7) using the shallow-ice approximation (SIA) is standard (Reference HutterHutter, 1983; Reference MorlandMorland, 1984). A standard derivation yields a formula for the ice flux q,
where
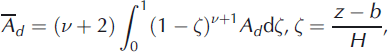
where z is elevation, b is bed elevation and C is normalized elevation. If instead we are dealing with sliding, then
and use of the continuity equation
results in the nonlinear diffusion-type equation (7). Linearizations are computed by expanding H and a in series
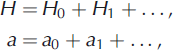
and truncating at first order. The zeroth-order and first-order equations are
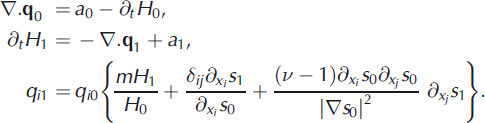
We estimate q 0 using the procedure described above. A very significant and convenient feature of the perturbation equation is the absence of the rate factor in the first-order equation, meaning that we do not have to estimate it. This form shows how correct estimation of current fluxes is crucial to forecasting. Additionally, the use of a linearized model means that the evolution equations do not need to specify whether or not basal sliding is occurring. All rates are determined by the ice flux, which we derive directly from the data.
The first-order flux equation (16) can be discretized and solved numerically using an unconditionally stable implicit method. These are linear equations, so the matrix expression of the discretized equation only has to be computed and factorized once. The stable marching scheme for this linear equations set means that there are no time-step limits on the evolution, and they are constrained by the yearly averaging of the forecast accumulation, expressed in the surface mass-balance anomaly a 1. The thickness anomaly is expressed by the quantity H 1.
3.4. Time-dependent modelling and outline of experiments
By construction, initialization puts the perturbed model into steady state. It is then forced by either introducing a surface mass-balance anomaly or moving the grounding line. Our procedure of investigating the inland consequences of instantaneous grounding-line retreat is readily incorporated by forcing the thickness anomalies H 1 in the zones downstream of the prescribed new grounding line such that the original ice surface plus anomaly are at sea level. We did not know the bathymetry well enough to make it meaningful to correct the thickness anomaly to account for the ice freeboard. Since volume contributions from the loss of the outlet glaciers themselves are small, this correction is not of quantitative significance to our quoted sea-level contributions. By using the procedures listed here, volume change above sea level and the evolution of H 1 upstream of the new grounding line are computed.
The approach of applying plausible retreat scenarios of imposed instantaneous grounding-line retreat and computing their upstream effects is necessary due to the absence of accurate bed topographic data. As we use surface velocities to direct ice flux, and then calculate the flux from balance requirements, we do not need to have a very accurate estimate of ice thickness. The linearized evolution equation does include ice thickness, but only as a divisor in one term. Compared to a more conventional ice model (where ice thickness appears in the flux formula raised to the power five), it is apparent that our approach is far less sensitive to poor ice thickness data. The perturbed flux in the linearized flux equation depends on the observed surface elevation and ice thickness, but it is generally more sensitive to the surface elevation. In consequence, the whole response is less sensitive to our choice of bed topography. Since we consider linear equations, solutions are superposable, and we undertake the simulations separately for each chosen basin. This also allows us to compute the response of the APIS to instantaneous grounding-line retreat at individual drainage basins independently of specifying the timing of the retreat, on a basin-by-basin basis.
Time-dependent experiments consisted of forcing with surface mass-balance rate anomalies, grounding-line retreat, and ice-shelf collapse of 20 selected outlet glacier basins (Fig. 1). These 20 basins were selected as they are likely to have the greatest consequences for sea-level change over centennial timescales. The surface mass-balance scenarios consisted of four experiments: two using RACMO2 forced by ECHAM5, and two by HadCM3, using the E1 and A1B scenarios, starting with a zero surface anomaly and holding the position of the grounding line fixed. RACMO2 calculated surface mass balance on a 55 km grid using a multilayer surface and subsurface scheme, two-way coupled to an atmospheric scheme, and utilizing net surface energy fluxes to calculate melt, percolation, refreezing and meltwater runoff (Reference Ettema, Van den Broeke, Van Meijgaard, Van de Berg, Box and SteffenEttema and others, 2010). Surface mass-balance fields were linearly interpolated from the regional model grid to the ice-sheet model grid. RACMO2 has been shown to reproduce the spatial pattern, magnitude and timing of snowmelt in the AP (Reference BarrandBarrand and others, 2013), and to provide good agreement between modelled and in situ observations of surface mass balance throughout Antarctica (Reference Lenaerts, Van den Broeke, Van de Berg, Van Meijgaard and Kuipers MunnekeLenaerts and others, 2012). Surface mass-balance estimates in the northern part of Graham Land are, however, expected to be less well resolved due to poorer representation of coastal climate in the 55 km model grid. The grounding-line scenarios consisted of causing the grounding lines of the 20 selected glaciers to retreat by 10 km and by 20 km in two separate sets of experiments. Ice-shelf breakup scenarios consisted of ensemble calculations of the volumetric response of the 20 basins by 2100 and 2200 to shelf break-up over 50, 100 and 200 years.
4. Results and Discussion
4.1. Surface mass-balance scenarios
The responses of the APIS to surface mass-balance scenarios to the year 2200 are shown in Figure 4. The spread of model results from both global climate model projection and emissions scenario forcings is wide, with the caveat that intercomparison is not possible after 2100 due to the extrapolation of ECHAM5 surface mass-balance fields. The net sea-level contributions resulting from the volume response to surface mass-balance anomalies on the AP are predominantly negative as mass balance is expected to be dominated by increased accumulation throughout the next two centuries. The sea-level contribution from the APIS using HadCM3 surface mass-balance projections was more negative than that using ECHAM5 by 2100. This indicates that HadCM3 computed more positive surface mass balance than ECHAM5, resulting in greater growth of the ice sheet. HadCM3 mass balance was more positive than ECHAM5 to the extent that the aggressive mitigation scenario (E1) of HadCM3 resulted in similar volume gain (net sea-level fall) to the middle-of-the-road scenario of ECHAM5 by 2100.

Fig. 4. Response of AP ice sheet to 2200 to A1B and E1 surface mass-balance scenarios provided by RACMO2, forced with either HadCM3 or ECHAM5. (a) Contribution to sea level for all four scenarios. Solid line is computed sea-level contribution for the 20 largest drainage basins; dotted line is the sea-level contribution that would have occurred without ice-dynamical response. (b, d) Change in surface elevation (m) after 200 years for HadCM3 A1B and ECHAM5 E1 scenarios. (c, e) Net mass-balance anomalies (m of ice) for HadCM3 A1B and ECHAM5 E1 scenarios, to 2200.
Figure 4a shows a pair of curves for each simulation, representing the surface mass balance alone and the total mass balance including discharge at the grounding-line (dynamics). In each instance, projected volume gains of the ice sheet (negative net sea-level contribution) were larger when discharge was not considered. The dynamic response of the APIS therefore offsets the direct effect of increased accumulation, as discharge is increased. Increased discharge returns ∼15% of the mass gained at the surface to the sea by 2100, and ∼30% by 2200. The offsets between estimates with and without discharge at the grounding line increase according to the magnitude of the total sea-level contribution (i.e. HadCM3 A1B offset is larger than E1 offset). This shows that the relative importance of the ice-dynamical response for projections of sea-level change is dependent on the magnitude of projected surface mass-balance anomalies.
The curves illustrating the response of the APIS to mass-balance anomalies from ECHAM5 are broadly similar in both A1 B and E1 scenarios to ∼75 years (very slightly positive contribution to sea level). The curves then diverge between 75 and 100 years, with the A1B and E1 scenarios resulting in a negative sea-level contribution (−1 and ∼−0.5 mm, respectively). This result is expected as E1 is based on forecasts of aggressive emissions mitigation and thus is likely to project reduced accumulation compared to the A1 B scenario. Post-2100, ECHAM5-forced surface mass-balance fields are not considered true projections, however, due to extrapolation of model output (see Section 2).
HadCM3 forced projections, which are based on surface mass-balance anomalies computed for the full period between 2000 and 2200, are similar between A1B and E1 scenarios to around 2050. After 2050, however, surface mass-balance anomalies in the middle-of-the-road scenario become strongly positive due to increased accumulation, giving a negative net sea-level contribution from the APIS. While the rate of change of the contribution to sea level in the HadCM3 E1 scenario also increases post-2100, there is some variability in the slope of the curve, and the final net sea-level contribution at 2200 is −4 mm including ice-dynamic response, considerably less than the −12 mm from A1B. Projected surface mass balance of the AP is strongly dependent on the strength of westerlies predicted by each global climate model run, hence the large sensitivity between scenarios.
The spatial plots in Figure 4b–e illustrate the range of projected surface mass-balance anomalies and simulated elevation changes between 2000 and 2199 from the model runs giving the smallest projection of total sea-level contribution (ECHAM5, E1) and the largest projection (HadCM3, A1B). In Palmer Land, HadCM3 A1 B predicts a strong east– west contrast in surface mass-balance rate anomaly (Fig. 4c) which results in substantial thickening on the west side of Palmer Land (Fig. 4b). This anomaly and subsequent thickening is not seen in ECHAM5. ECHAM5 E1 predicts a negative mass-balance anomaly in the southwestern part of Palmer Land, and close to balance or slightly positive mass balance elsewhere on the AP (Fig. 4e). While there are areas of strongly negative mass balance in the northern part of Graham Land in the ECHAM5 simulations (associated with increases of both snowmelt and liquid precipitation), the smaller area means that this probably does not significantly impact on region-wide mass balance.
It is clear that our estimates of the likely sea-level contribution of the AP from changes in surface mass balance are strongly conditioned by the scenario and the model predicting the global circulation. None of the scenarios predicts a net positive sea-level contribution from the APIS. In fact in one case, the A1B scenario of HadCM3, a negative sea-level contribution of around −4 mm by 2100 and nearly −12 mm by 2200 is predicted. Increased glacier flow due to ice thickening returns ∼15% of the increased snowfall to the sea by 2100 and ∼30% by 2200. We believe these proportions are robust as they stem from our flux estimates, which are based on observed velocities.
4.2. Grounding-line retreat and ice-shelf break-up scenarios
In addition to changes in surface mass balance, APIS model simulations were performed with prescribed instantaneous grounding-line retreat of 10 and 20 km at each of the 20 largest drainage basins. The likely sea-level contribution resulting from the dynamic response of the APIS to a 10 km grounding-line retreat ranged between 0 and 1.5 mm per basin (Fig. 5a). The instantaneous response to such a perturbation was typically small, 0–0.25 mm of sea-level rise. The final volume change appeared to be somewhat controlled by the instantaneous response, with those basins experiencing the largest initial volume response also providing the largest contributions to sea-level rise by the end of the forecast period. There was high variability between individual basins, with several showing little or no change after 200 years (e.g. basins 8–10) and others providing up to 1.5 mm of sea-level equivalent (SLE) ice volume loss (basins 16 and 17).

Fig. 5. Response of AP ice sheet to 2200 to grounding-line retreat scenarios. (a) Response of AP basins to grounding-line retreat of 10 km (green crosses; lower cross is the instantaneous response, and upper cross is the volume response after 200 years). Red circles represent grounding-line retreats of 20 km; lower and upper circles represent instantaneous and 200 year sea-level contributions. (b) Rate of response of five selected drainage basins to grounding-line retreat over 200 years. Responses of basins 4, 8 and 20 are to a 10 km retreat; those of basins 12 and 16 are to a 20 km retreat. (c–e) Examples of surface elevation change response by 2200 of basins 11 (c), 7 (d) and 3 (e) to a 20 km grounding-line retreat.
When the grounding-line retreat was set to 20 km, initial volume losses of the ice sheet were typically larger than in the 10 km retreat scenario (on the order of 0.25–0.5 mm of sea-level change per basin), as were losses by 2200 (Fig. 5a). The largest changes forecast suggest that 2–4.5 mm of sea-level rise may result from 20 km grounding line retreat at some basins. The likely change in volume in response to this perturbation scenario is therefore 0.5–3 mm of SLE water per basin. Figure 5c–e show three examples of the inland propagation of thinning by 2200 in response to a 20 km grounding-line retreat. In each instance, the response of each drainage basin to the perturbation is substantial thinning (>150 m) at the former grounding-line position, with inland propagation of thinning extending tens of km upstream.
This sample is a geographically realistic representation of change in the APIS forced by less realistic perturbations at the larger drainage basins of the southern AP. We have assumed very rapid (instantaneous) retreat of the grounding line, followed by stasis, and calculated the ensuing changes in volume upstream. These volume changes are much larger (up to 4.5 mm) than those arising from the initial retreat (up to a few tenths of a milllimetre). Our problem in turning this into a forecast is that we are not able to estimate the timing of shelf retreat, or, without further information, the magnitude of the initial retreat. Our results show that for smaller retreat, steady-state response is achieved within a few decades, while for larger retreat the adjustment is still continuing at 2200 (Fig. 5b). The use of 10 km and 20 km as retreats is only indicative. There may be areas bordering the George VI Ice Shelf where grounding-line retreat may exceed 20 km (Fig. 3b), especially following loss of the confined ice shelf. Likewise, if bed topography of the larger outlet glaciers on the AP is deeper than existing sparse observations suggest, grounding-line retreat scenarios may exceed our indicative estimates.
Using an ensemble of 10 000 calculations for forecast periods to 2100 and 2200, we also investigated the sensitivity of response of the APIS to three ice-shelf break-up scenarios applied to the 20 selected drainage basins (Fig. 6). The ensemble calculations exploited the superposability property of linear equations to sum the contributions of the basins. Superposability exists in both time and space, so each of the perturbed outlet glaciers had its shelf ice removed at a randomly chosen time over the given period. The volume contribution then depended on the projection time (2100 or 2200) and the time at which the outlet glacier retreated. We considered contributions to 2100 and 2200, with scenarios of (1) outlet glaciers all retreating in 2020 (an extreme case); (2) all outlet glaciers having retreated by 2050; and (3) outlet glaciers having retreated by the end of the projection period (2100 or 2200). These gave rise to a probability distribution of sea-level contributions, with spread increasing with the time period over which the outlet glaciers were permitted to retreat. Ensembles of 10 000 members were used; this was not computationally taxing owing to our exploitation of the superposability property, and the results from smaller ensembles were not markedly different.

Fig. 6. Results of ensemble calculations, expressed as bin populations, of ice-shelf break-up combined with a 20 km grounding-line retreat in the 20 selected basins. (a, c) Forecasts to 2100; (b, d) forecasts to 2200. (a, b) Break-up over the forecast period; (c, d) break-up over 50 years. Histograms computed from samples of 10000.
Given that all but one of the 20 drainage basins chosen for analysis terminate into floating shelf ice (see Fig. 1), this experiment was applied to these 19 basins, and the volume response of the entire APIS calculated. We assumed breakup of all ice shelves into which our 20 selected glaciers flow, within 50, 100 and 200 years of the year 2000. Considering a medium break-up scenario (all shelves to break up by 2100) and a coincident 10 (20) km retreat of the grounding line, the average sea-level rise contribution per drainage basin was 5 (20) mm by 2100 (Fig. 6a). For a faster break-up (all shelves to break up by 2050), the basin-averaged sea-level rise contribution by 2100 was 7 (25) mm (Fig. 6c). Running our forecast simulations to the end of 2200, the fast break-up scenario (50 years) and slow break-up scenario (200 years) resulted in basin-averaged sea-level rise contributions of, respectively, 8 (31) mm and 7 (24) mm (Fig. 6d and b). Simulations run with all shelves breaking up by 2020 resulted in a total contribution to sea level from the APIS of 7 (25) mm by 2100, and 8 (32) mm by 2200. Inclusion of the smaller drainage basins of the AP into this calculation would increase the total sea-level rise contribution, but is unlikely to result in sea-level contribution greater than 40 mm by 2100, or 50 mm by 2200, even with the 20 km grounding-line retreat scenario. It is difficult to assign the most probable values of future sea-level rise from grounding-line retreat and ice-shelf break-up scenarios given the difficulty of predicting the timing of these conjectural events. However, values between 10 and 20 mm of SLE water from grounding-line retreat alone seem plausible.
While surface mass-balance scenarios predicted a negative net contribution to sea level from the APIS during the next two centuries, it is important to note that at present the ice of the peripheral islands of the AP (Reference Hock, De Woul, Radić and DyurgerovHock and others, 2009), glaciers draining into the Larsen A and B embayments (Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011; Reference Shuman, Berthier and ScambosShuman and others, 2011) and both the APIS and islands combined (Reference Ivins, Watkins, Yuan, Dietrich, Casassa and RülkeIvins and others, 2011) are contributing to sea-level rise. Continental-scale estimates suggest that the AP contributes ∼25% of the total mass loss from Antarctica (Reference RignotRignot and others, 2008). While accumulation is known to be increasing in some areas (e.g. Reference Thomas, Marshall and McConnellThomas and others, 2008), this is likely counteracted by increased ablation at lower elevations (Reference Hock, De Woul, Radić and DyurgerovHock and others, 2009) along with drawdown of glaciers draining into the Larsen B embayment (Reference Rott, Müller, Nagler and FloricioiuRott and others, 2011; Reference Shuman, Berthier and ScambosShuman and others, 2011; Reference Berthier, Scambos and ShumanBerthier and others, 2012) and non-positive mass budget of glaciers flowing into the George VI Ice Shelf (Reference RignotRignot and others, 2008). Continued monitoring, improved ice thickness measurements, and more detailed information on ice–ocean interactions at the glacier front are essential in order to characterize future dynamic mass losses as accumulation continues to increase. While the role of the ocean is implicit in our prescribed grounding-line retreat and ice-shelf collapse scenarios, future work considering regional variability in ocean temperatures and ice–ocean interactions may improve our predictive modelling efforts.
5. Conclusions
We have computed future contributions to sea level from the APIS with an ice flow model directly initialized using a newly developed technique which calculates ice fluxes based on observed surface elevation and velocity and computes volume response using a linearized technique. Volume change estimates resulting from surface mass-balance anomalies depend strongly on the scenario used and the model forcing that scenario. No scenario predicted a positive contribution to sea level from the AP ice sheet. The range of calculated volume responses to surface mass-balance anomalies predicted negative sea-level contribution between 0 and −4 mm by 2100 and between −0.5 and −12 mm by 2200. Improvement of these results depends mainly on improved meteorological modelling, as the glacial response is strongly conditioned by the present flux through the ice sheet. Estimates of the mass-balance response to grounding-line retreat are highly uncertain given our poor knowledge of bedrock topography, uncertainty of retreat scenarios, and uncertainty about the timing of ice-shelf break-up. We suggest upper limits to the sea-level contribution from the APIS from grounding-line retreat and ice-shelf break-up of 40 mm by 2100 and 50 mm by 2200, with more probable values around half this. Therefore, unless a major confined ice shelf such as George VI is lost, increased snowfall on the AP has the potential to offset ice-dynamical contributions to sea-level rise in the coming two centuries, but values are uncertain and subject to revision.
Acknowledgements
This work was supported by funding from the ice2sea programme from the European Union 7th Framework Programme grant No. 226375, the British Antarctic Survey Polar Science for Planet Earth programme, and the Netherlands Polar Program of the Netherlands Organization for Scientific Research (NWO/ALW). This is ice2sea contribution No. 126. We thank an anonymous reviewer and Graham Cogley for comments which improved the manuscript.











