1. INTRODUCTION
Nye (Reference Nye2015) constructed an approximate plane flow velocity distribution near the glacier terminus consistent with Glen (Reference Glen1961)'s measured profile and surface velocity distributions on Austerdalsbreen in 1958 and 1959. He adopts the conventional viscous power law for the ice, assumed to be close to melting so the temperature-dependent rate factor is constant (unity). It is then assumed that the driving shear stress is that given by the reduced model, an expression valid for small surface and bed undulation slopes relative to a mean bed plane which is close to horizontal. The next key simplification is that the longitudinal strain-rate is constant, independent of depth, defined by the observed, approximately constant, surface velocity gradient. This is incorporated in the viscous relation to construct, independent of any further prescribed surface and bed conditions, a non-laminar flow field from which a realistic compressive longitudinal stress magnitude is obtained.
An immediate question is whether it is necessary to make this longitudinal strain-rate simplification, or any alternative simplification. It is not. A plane flow local reduced model solution is now constructed for the terminus vicinity – an observation region – assuming a known surface profile and known surface tangential velocity at the observation time t = 0; a snapshot of the flow. The local reduced model is a set of leading order relations in a small parameter ε, which neglects terms of order ε compared with unity. ε is a co-ordinate and velocity scaling factor which is determined by the small dimensionless viscosity ν incorporating the observation region thickness magnitude d 0.The validity of the local reduced model requires that the slopes of the bed undulations relative to the mean bed plane are not greater than ε in magnitude. There is no reference to conditions upstream of the observation region. Distinct balances arise for mean bed planes close to horizontal, slopes of order ε as in the above application and for steep glaciers with bed plane slope of order unity, but only the former relevant to Nye (Reference Nye2015)'s application is presented. The solution is achieved by Taylor series expansions in an upstream dimensionless distance ξ from the (moving) terminus, which covers a few thickness magnitudes. The Taylor series expansions in ξ are truncated when the next term does not exceed ε in magnitude. A bed tangential condition, such as a sliding law, is not required in this solution, but the solution incorporates the tangential traction and velocity at the bed and so imposes restrictions on any such relation. Further, the asymptotic expansion of the unsteady profile equation then determines the terminus velocity and instantaneous rate of change of the profile in terms of the net ablation/accumulation at the terminus and provides the criterion for the retreat/advance change-over. Analogous analyses can be performed for other two-dimensional flows, for example those describing a terminus spreading with radial or elliptic symmetry.
This observation region flow analysis is therefore of wider generality than Nye (Reference Nye2015)'s flow deduction for Austerdalsbreen, but comparison with the latter is used for illustration. In particular, the validity of the simplification and its consequences are noted.
2. TERMINUS VICINITY FLOW
Morland and Johnson (Reference Morland and Johnson1980) developed the reduced model for steady plane flow of an ice sheet over a flat bed, then Morland and Johnson (Reference Morland and Johnson1982) incorporated bed topography for near horizontal and steep mean bed planes. Subsequently, Morland (Reference Morland1984) presented the corresponding analysis for general three-dimensional unsteady flow over an inclined mean bed plane with arbitrary slope relative to the horizontal. The trivial solution of a horizontal ice surface – an ice reservoir – can be rejected by co-ordinate and velocity component scalings involving a small parameter ε related to a small dimensionless ice viscosity factor ν. Hutter (Reference Hutter1981, Reference Hutter1983) introduced this co-ordinate and velocity stretching directly to reflect the large aspect ratio of an ice sheet, described as the shallow ice approximation (SIA). Here it is only a terminus vicinity flow which is being constructed independent of the likely complex upstream flow over varying bed slopes, but this can be described by a local reduced model derived by the same analysis with a length scale defined by the thickness magnitude of the observation region. The dimensionless reduced model relations derived by Morland (Reference Morland1984) will be adopted as a starting point. A plane flow approximation is adopted, as in Nye (Reference Nye2015), but analogous analyses follow for a terminus spreading with radial or elliptic symmetry, or any one-dimensional spreading.
The plane flow is described in rectangular Cartesian co-ordinates (x,z) with the x-axis pointing down a mean bed plane inclined at an angle χ to the horizontal, as shown in Figure 1. The associated velocity components are (u, w) with the velocity normal to the x, z plane v = 0. The origin represents the start of the glacier terminus vicinity – the observation region – over which the ice thickness reaches a magnitude d 0; the Austerdalsbreen data d 0 = 60 m is adopted for calculation. The moving terminus at time t is defined by x = x M(t), with x M(0) the observed location. The fixed bed is z = f(x), not necessarily plane, but with only undulations ofa small slope, and the unsteady glacier surface is z = h(x, t), also with small slope imposed by the reduced model equations. The slopes are exaggerated in the figure. Nye (Reference Nye2015) adopts an approximation tan χ = 0.095 based on his later bed profile measurements, and a constant surface slope γ = 0.182 relative to the bed at the observation time t = 0, shown in Figure 1. This corresponds to a constant surface slope with tangent 0.282 relative to the horizontal. Note that the surface slope 0.182 relative to the bed plane is not very small, so a reduced model which neglects terms of this magnitude compared with unity is only a rough approximation. Here a plane bed with small slope 0.095 is again adopted for illustration, but the ice surface is not assumed to be plane. The asymptotic analysis is performed retaining terms with magnitudes greater than or equal to ε so as not to compound the reduced model errors.
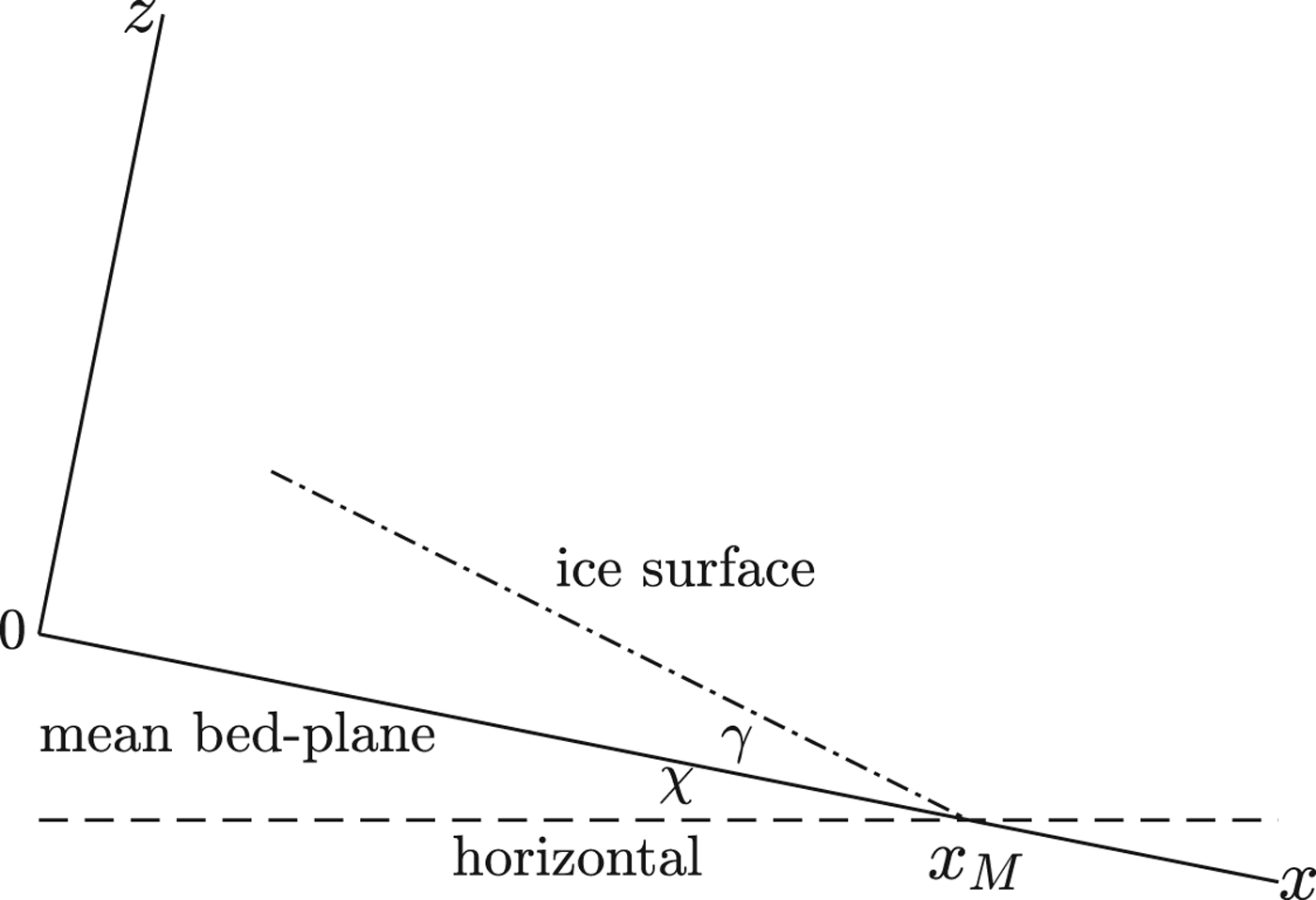
Fig. 1. Plane co-ordinate system (x, z) with x-axis down mean bed plane, showing ice surface and the horizontal from terminus location x M at time t = 0. Slopes are exaggerated.
The ice is assumed to be incompressible with density ρ = 918 kgm−3, so the pressure p is a workless constraint not given by a constitutive law, but determined by momentum balance and boundary conditions. The deviatoric response is defined by a non-linearly viscous fluid relation between the strain-rate tensor D and the deviatoric stress tensor ![]() $ {\hat {\bi \sigma} } = {\bi \sigma } + p {\bi I} $, where σ is the Cauchy stress and I is the unit tensor. It is assumed that the ice in the terminus vicinity is temperate so the temperature dependent rate factor is unity. The conventional simplifications that D is co-axial with
$ {\hat {\bi \sigma} } = {\bi \sigma } + p {\bi I} $, where σ is the Cauchy stress and I is the unit tensor. It is assumed that the ice in the terminus vicinity is temperate so the temperature dependent rate factor is unity. The conventional simplifications that D is co-axial with ![]() $ {\hat {\bi \sigma }}$, and the viscosity coefficient depends only on the second principal invariant J of
$ {\hat {\bi \sigma }}$, and the viscosity coefficient depends only on the second principal invariant J of ![]() $ {\hat {\bi \sigma }}$, are adopted. The viscous law in dimensionless form is
$ {\hat {\bi \sigma }}$, are adopted. The viscous law in dimensionless form is
 $$ \displaystyle{{\bi D} \over {D_{0}}} = \psi({J}) {\displaystyle{ {\hat{ \bi \sigma}} \over {\sigma_{0}}}}, \quad {J} = {\displaystyle {{1} \over {2}}}{tr} \left(\displaystyle{ {\hat{\bi \sigma}} \over {\sigma_{0}}}\right)^{2}, $$
$$ \displaystyle{{\bi D} \over {D_{0}}} = \psi({J}) {\displaystyle{ {\hat{ \bi \sigma}} \over {\sigma_{0}}}}, \quad {J} = {\displaystyle {{1} \over {2}}}{tr} \left(\displaystyle{ {\hat{\bi \sigma}} \over {\sigma_{0}}}\right)^{2}, $$where the units σ 0 and D 0 are chosen so that the constitutive function ψ(J) is of order unity for deviatoric stresses and strain-rates arising in typical ice sheet flows; namely
From Morland and Johnson (Reference Morland and Johnson1980), the customary Glen's power law, (Glen, Reference Glen1955, Reference Glen1958), based on his laboratory experiments on ice close to melting, adopted by Nye (Reference Nye2015), is given by
which has an infinite viscosity at zero stress giving rise to singularities at the free surface. An alternative expression with smaller least squares error to the same data over a shear stress range 0–5 × 105 Nm−2, 0 ≤ J ≤ 25, is the polynomial (Smith and Morland, Reference Smith and Morland1981) :
which has the mathematical advantage of a finite viscosity at zero stress. Solutions for both laws will be derived.
3. REDUCED MODEL
First introduce normalised dimensionless stress, strain-rate and time variables, denoted by an overbar:
where g = 9.81 ms−2 and q 0 = 1 ma−1 is an accumulation/melt magnitude. Note that atmospheric pressure p a = 1.013 × 105 Nm−2, assumed constant over the terminus vicinity, is not negligible compared with ice overburden pressure for these depths of ice, unlike the situation for large thick ice sheets; pointed out to me by Nye (personal communication). The viscous relation (1) now becomes
 $$ \eqalign{& {\bar{\bi D}} = \nu^{-1} \,\psi(J) {\hat{\bar{\bi \sigma}}}, \quad \nu = \displaystyle{ {{{\sigma}_0} q_0} \over {\rho g {d_{0}}^2 D_0}} = 0.003, \cr & J = \displaystyle{{1} \over {2}} \left( \displaystyle{{\rho g d_{0}} \over {\sigma}_{0}}\right)^{2} {tr}( {\hat{\bar{ \bi \sigma}}})^{2},} $$
$$ \eqalign{& {\bar{\bi D}} = \nu^{-1} \,\psi(J) {\hat{\bar{\bi \sigma}}}, \quad \nu = \displaystyle{ {{{\sigma}_0} q_0} \over {\rho g {d_{0}}^2 D_0}} = 0.003, \cr & J = \displaystyle{{1} \over {2}} \left( \displaystyle{{\rho g d_{0}} \over {\sigma}_{0}}\right)^{2} {tr}( {\hat{\bar{ \bi \sigma}}})^{2},} $$where ν is a small dimensionless viscosity. Formal series expansions in ν results in an ice reservoir with horizontal surface – no descent to a terminus, and it follows that a non-horizontal surface requires co-ordinate and velocity scalings
where the capital variables and gradients are order unity. The viscous law (6) then becomes
 $$ \eqalign{&{\bar{\bi D}} = \nu^{-1}\,\psi( {\vartheta} {\check J}) {\hat{\bar{\bi \sigma}}}, \quad {\check J} = \displaystyle{{1} \over {2}}{\rm tr} \left(\displaystyle{ {\hat{\bar{\bi \sigma}}} \over { {\epsilon}}}\right)^{2}, \cr & {\vartheta} = \left( \displaystyle{\rho g d_{0}} \over {\sigma_{0}}\right)^{2}\, {\epsilon}^{2} = 29.2\, {\epsilon}^{2}.} $$
$$ \eqalign{&{\bar{\bi D}} = \nu^{-1}\,\psi( {\vartheta} {\check J}) {\hat{\bar{\bi \sigma}}}, \quad {\check J} = \displaystyle{{1} \over {2}}{\rm tr} \left(\displaystyle{ {\hat{\bar{\bi \sigma}}} \over { {\epsilon}}}\right)^{2}, \cr & {\vartheta} = \left( \displaystyle{\rho g d_{0}} \over {\sigma_{0}}\right)^{2}\, {\epsilon}^{2} = 29.2\, {\epsilon}^{2}.} $$where for the power law given by (3) and the polynomial law given by (4),
 $$ \eqalign{&(3): {\epsilon} = \nu^{{n}/({n+1})} = 0.012, \quad {\vartheta} = 0.004; \cr & (4): {\epsilon} = \nu^{1/2} = 0.055, \quad {\vartheta} = 0.088.} $$
$$ \eqalign{&(3): {\epsilon} = \nu^{{n}/({n+1})} = 0.012, \quad {\vartheta} = 0.004; \cr & (4): {\epsilon} = \nu^{1/2} = 0.055, \quad {\vartheta} = 0.088.} $$but any small-scale factor ε of similar magnitude provides the magnitude balance. It will be convenient to investigate both laws with a common scale factor ε = 0.04.
Now ![]() $ {\bar D}_{xx} = - {\bar D}_{zz} = O(1)$ so
$ {\bar D}_{xx} = - {\bar D}_{zz} = O(1)$ so ![]() $ {\bar \sigma }_{xx} = - {\bar \sigma }_{zz} = O( {\epsilon }^{2})$, and assuming small mean bed inclination χ, of order ε or less, the lead order two-dimensional mass and momentum balances are
$ {\bar \sigma }_{xx} = - {\bar \sigma }_{zz} = O( {\epsilon }^{2})$, and assuming small mean bed inclination χ, of order ε or less, the lead order two-dimensional mass and momentum balances are
 $$ \eqalign{& {\displaystyle{\partial {U} \over {\partial {X}}}} + {\displaystyle{\partial {W}} \over {\partial {Z}}} = 0, \quad {\displaystyle{\partial { \bar \sigma}_{xz} \over {\partial {Z}}}} - {\epsilon}{\displaystyle{{\partial {\bar p}} \over {\partial {X}}}} + {\sin}\,\chi = 0, \cr & {\displaystyle{\partial { {\bar p}} \over {\partial {Z}}}} + {\cos}\,\chi = 0.} $$
$$ \eqalign{& {\displaystyle{\partial {U} \over {\partial {X}}}} + {\displaystyle{\partial {W}} \over {\partial {Z}}} = 0, \quad {\displaystyle{\partial { \bar \sigma}_{xz} \over {\partial {Z}}}} - {\epsilon}{\displaystyle{{\partial {\bar p}} \over {\partial {X}}}} + {\sin}\,\chi = 0, \cr & {\displaystyle{\partial { {\bar p}} \over {\partial {Z}}}} + {\cos}\,\chi = 0.} $$These are subject to surface and bed conditions, treating the surface slope relative to the inclined bed plane, θ, as order ε,
 $$ \eqalign{& Z = H(X, {\bar t}): {\bar p} = {\bar p}_a = 0.187, \quad {\bar \sigma}_{xz} = 0, \cr & \displaystyle{{\partial {H}} \over {\partial {\bar t}}} + U\displaystyle{{\partial {H}} \over {\partial {X}}} - W = Q_n,} $$
$$ \eqalign{& Z = H(X, {\bar t}): {\bar p} = {\bar p}_a = 0.187, \quad {\bar \sigma}_{xz} = 0, \cr & \displaystyle{{\partial {H}} \over {\partial {\bar t}}} + U\displaystyle{{\partial {H}} \over {\partial {X}}} - W = Q_n,} $$where Q n and B n are dimensionless fluxes, and ![]() $U_{b}(X,\, {\bar t})$ is the dimensionless velocity along the bed, all with unit q 0.
$U_{b}(X,\, {\bar t})$ is the dimensionless velocity along the bed, all with unit q 0. ![]() $ {\bar p}_b$ is the dimensionless total pressure on the bed where
$ {\bar p}_b$ is the dimensionless total pressure on the bed where ![]() $ {\bar p}_{b} - {\bar p}_{a}$ is that due to the ice overburden. The actual relation, function F, will not be required, but the solution imposes restrictions on F. The lead order viscous relation becomes
$ {\bar p}_{b} - {\bar p}_{a}$ is that due to the ice overburden. The actual relation, function F, will not be required, but the solution imposes restrictions on F. The lead order viscous relation becomes
With the restriction χ = O(ε), ε −1sin χ is order unity, while cos χ = 1, neglecting ε 2, but is retained. Then integrating (10)2 and (10)3 in turn through the depth and applying the surface traction conditions (11) and the bed flux condition (12)1 gives the lead order stress expressions
Different expressions are obtained for a steep glacier bed χ = O(1). From (14) and (15) the tractions on the bed Z = 0 are
and hence ![]() $H(X,\, {\bar t})$ determines the pressure on the bed, and
$H(X,\, {\bar t})$ determines the pressure on the bed, and ![]() $H(X,\, {\bar t})$ and
$H(X,\, {\bar t})$ and ![]() $ \Gamma (X,\, {\bar t})$ determine the shear traction on the bed, independent of any prescribed sliding law.
$ \Gamma (X,\, {\bar t})$ determine the shear traction on the bed, independent of any prescribed sliding law.
Define
then ![]() $ {\check J} = \tau ^2$and the viscous relation (13) is
$ {\check J} = \tau ^2$and the viscous relation (13) is
Integrating (18) with respect to Z from the bed Z = 0:
 $$ \eqalign{& U(X,Z, {\bar t}) = U_b(X, {\bar t}) + g_{1}(X,Z, {\bar t}), \cr & g_{1}(X,Z, {\bar t}) = \int_{0}^{Z} g(X,Z^{\prime}, {\bar t}) {d}Z^{\prime}.} $$
$$ \eqalign{& U(X,Z, {\bar t}) = U_b(X, {\bar t}) + g_{1}(X,Z, {\bar t}), \cr & g_{1}(X,Z, {\bar t}) = \int_{0}^{Z} g(X,Z^{\prime}, {\bar t}) {d}Z^{\prime}.} $$Incompressibility (10) is satisfied by introducing a stream function ![]() $ \omega (X,\,Z,\, {\bar t})$ such that
$ \omega (X,\,Z,\, {\bar t})$ such that
then integrating again with respect to Z:
 $$ \eqalign{&\omega(X,Z, {\bar t}) = \omega_{\rm b}(X, {\bar t}) + Z\,U_{\rm b}(X, {\bar t}) + g_{2}(X,Z, {\bar t}), \cr & \quad g_{2}(X,Z, {\bar t}) = \int_{0}^{Z} g_{1}(X,Z^{\prime}, {\bar t}) {d}Z^{\prime},} $$
$$ \eqalign{&\omega(X,Z, {\bar t}) = \omega_{\rm b}(X, {\bar t}) + Z\,U_{\rm b}(X, {\bar t}) + g_{2}(X,Z, {\bar t}), \cr & \quad g_{2}(X,Z, {\bar t}) = \int_{0}^{Z} g_{1}(X,Z^{\prime}, {\bar t}) {d}Z^{\prime},} $$where ![]() $ \omega _{\rm b}(X,\, {\bar t}) $ is the stream function value on the bed. Now the surface and bed kinematic conditions (11)3 and (12)1 are expressed by
$ \omega _{\rm b}(X,\, {\bar t}) $ is the stream function value on the bed. Now the surface and bed kinematic conditions (11)3 and (12)1 are expressed by
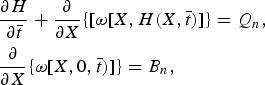 $$ \eqalign{& {\displaystyle{\partial {H}} \over {\partial { {\bar t}}}} + {\displaystyle{\partial} \over {\partial X}}\{[ \omega[X,H(X, {\bar t})]\} = Q_n, \cr & {\displaystyle{\partial} \over {\partial X}}\{ \omega[X,0, {\bar t})]\} = B_n,} $$
$$ \eqalign{& {\displaystyle{\partial {H}} \over {\partial { {\bar t}}}} + {\displaystyle{\partial} \over {\partial X}}\{[ \omega[X,H(X, {\bar t})]\} = Q_n, \cr & {\displaystyle{\partial} \over {\partial X}}\{ \omega[X,0, {\bar t})]\} = B_n,} $$then differencing and eliminating ω by (21)1 gives the profile equation
 $$ \eqalign{& {\displaystyle{\partial {H}} \over {\partial { {\bar t}}}} + {\displaystyle{{\partial} \over {\partial X}}}\{H(X, {\bar t})U_{\rm b}(X, {\bar t}) + g_{2}[X,H(X, {\bar t}), {\bar t}]\} \cr & = Q_n- B_n = -\bar{B}(X, {\bar t}),} $$
$$ \eqalign{& {\displaystyle{\partial {H}} \over {\partial { {\bar t}}}} + {\displaystyle{{\partial} \over {\partial X}}}\{H(X, {\bar t})U_{\rm b}(X, {\bar t}) + g_{2}[X,H(X, {\bar t}), {\bar t}]\} \cr & = Q_n- B_n = -\bar{B}(X, {\bar t}),} $$where ![]() $\bar {B}(X,\, {\bar t})$ is the net dimensionless melt flux.
$\bar {B}(X,\, {\bar t})$ is the net dimensionless melt flux.
4. TERMINUS ASYMPTOTICS
As near a divide and near a free surface, near the terminus the reduced model approximation is not valid – an inner boundary layer asymptotic expansion is required to be matched with the outer reduced model solution. However, in all these cases, the inner boundary layer expansion is passive. That is, the reduced model relations continue to satisfy all the boundary conditions through the inner boundary layer, so the outer reduced model solution is not influenced by matching with the boundary layer expansion. The inner region approximation of the full equations is, of course ,different from the reduced model solution, but here only in some small vicinity of the terminus not likely containing data points. Following is the reduced model analysis which will apply except in some small vicinity of the terminus.
First express variables as functions of the dimensionless time ![]() $ {\bar t}$ and a dimensionless distance ξ from the moving terminus
$ {\bar t}$ and a dimensionless distance ξ from the moving terminus ![]() $X = {X_{m}( {\bar t})}$, denoted by an over-check, and set X m(0) = 0; thus
$X = {X_{m}( {\bar t})}$, denoted by an over-check, and set X m(0) = 0; thus
 $$ \eqalign{& \xi = X_{m}( {\bar t}) - X, \quad H(X, {\bar t}) = {\check{H}}(\xi, {\bar t}), \cr & \Gamma(X, {\bar t}) = -{\displaystyle{\partial { {\check{H}}}} \over {\partial {\xi}}} =- {\check{\Gamma}}(\xi, {\bar t}),} $$
$$ \eqalign{& \xi = X_{m}( {\bar t}) - X, \quad H(X, {\bar t}) = {\check{H}}(\xi, {\bar t}), \cr & \Gamma(X, {\bar t}) = -{\displaystyle{\partial { {\check{H}}}} \over {\partial {\xi}}} =- {\check{\Gamma}}(\xi, {\bar t}),} $$ $$ \eqalign{&\displaystyle{{\partial {H}} \over {\partial { {\bar t}}}} = \displaystyle{{\partial { {\check H}}} \over {\partial { {\bar t}}}}+ {X_{m}^{\prime}( {\bar t})} {\check{\Gamma}}(\xi, {\bar t}), \cr & U(X,Z, {\bar t}) = {\check U}(\xi,Z, {\bar t}), \quad W(X,Z, {\bar t}) = {\check W}(\xi,Z, {\bar t}).} $$
$$ \eqalign{&\displaystyle{{\partial {H}} \over {\partial { {\bar t}}}} = \displaystyle{{\partial { {\check H}}} \over {\partial { {\bar t}}}}+ {X_{m}^{\prime}( {\bar t})} {\check{\Gamma}}(\xi, {\bar t}), \cr & U(X,Z, {\bar t}) = {\check U}(\xi,Z, {\bar t}), \quad W(X,Z, {\bar t}) = {\check W}(\xi,Z, {\bar t}).} $$Glen (Reference Glen1961)'s Austerdalsbreen measurements cover a distance 4 d 0 from the terminus at time ![]() $ {\bar t} = 0$, equivalent to ξ = 4ε ≈ 0.16 with a mean ε = 0.04 from (9). So consider a Taylor series expansion in small ξ for the profile :
$ {\bar t} = 0$, equivalent to ξ = 4ε ≈ 0.16 with a mean ε = 0.04 from (9). So consider a Taylor series expansion in small ξ for the profile :
 $$ \eqalign{& {\check H}(\xi, {\bar t}) = H_{1}( {\bar t})\xi + H_{2}( {\bar t})\xi ^{2} + H_{3}( {\bar t})\xi ^{3} + O(\xi^{4}), \cr & {\check{\Gamma}}(\xi, {\bar t}) = H_{1}( {\bar t}) + 2H_{2}( {\bar t})\xi + 3H_{3}( {\bar t})\xi ^{2} + O(\xi^{3}),} $$
$$ \eqalign{& {\check H}(\xi, {\bar t}) = H_{1}( {\bar t})\xi + H_{2}( {\bar t})\xi ^{2} + H_{3}( {\bar t})\xi ^{3} + O(\xi^{4}), \cr & {\check{\Gamma}}(\xi, {\bar t}) = H_{1}( {\bar t}) + 2H_{2}( {\bar t})\xi + 3H_{3}( {\bar t})\xi ^{2} + O(\xi^{3}),} $$where the coefficients at ![]() $ {\bar t} = 0$, H 1(0), H 2(0) and H 3(0), are determined by correlation with measured profile data; Glen (Reference Glen1961)'s profile data are used in the later illustration for comparison with Nye (Reference Nye2015)'s solution. A profile expansion to order ξ 3, slope to order ξ 2 and down-surface velocity expansion to order ξ 2, results in a balance to order ξ 2 of the profile equation (23). That is, an error of order ξ 3 compared with unity, with maximum value 0.004.
$ {\bar t} = 0$, H 1(0), H 2(0) and H 3(0), are determined by correlation with measured profile data; Glen (Reference Glen1961)'s profile data are used in the later illustration for comparison with Nye (Reference Nye2015)'s solution. A profile expansion to order ξ 3, slope to order ξ 2 and down-surface velocity expansion to order ξ 2, results in a balance to order ξ 2 of the profile equation (23). That is, an error of order ξ 3 compared with unity, with maximum value 0.004.
 $$ \eqalign{& \tau(X, {\bar t}) = {\check \tau} (\xi,Z, {\bar t})= {\check \tau}_{{\rm s}}(\xi, {\bar t}) [ {\check H}(\xi, {\bar t}) - Z], \cr & {\check \tau}_{{\rm s}}(\xi, {\bar t}) = \tau_{{\rm s}}(X, {\bar t}), \quad {\check{g}}(\xi,Z, {\bar t}) = {\check \tau}\psi( {\vartheta} {\check \tau}^{2}),} $$
$$ \eqalign{& \tau(X, {\bar t}) = {\check \tau} (\xi,Z, {\bar t})= {\check \tau}_{{\rm s}}(\xi, {\bar t}) [ {\check H}(\xi, {\bar t}) - Z], \cr & {\check \tau}_{{\rm s}}(\xi, {\bar t}) = \tau_{{\rm s}}(X, {\bar t}), \quad {\check{g}}(\xi,Z, {\bar t}) = {\check \tau}\psi( {\vartheta} {\check \tau}^{2}),} $$and by (15) τ s is order unity, so by (26) and (27), ![]() $ {\check \tau }$ is order ξ. For the power law,
$ {\check \tau }$ is order ξ. For the power law,
 $$ \eqalign{&{\bar g}( X,Z, {\bar t}) = {\check g}(\chi,Z, {\bar t}) = a_{0} {\check \tau}^{n} \lt O(\xi^{3}), \cr & a_0 = 3k(3 {\vartheta})^{({n-1})/{2}} = 0.947,} $$
$$ \eqalign{&{\bar g}( X,Z, {\bar t}) = {\check g}(\chi,Z, {\bar t}) = a_{0} {\check \tau}^{n} \lt O(\xi^{3}), \cr & a_0 = 3k(3 {\vartheta})^{({n-1})/{2}} = 0.947,} $$so ![]() $ {\check g}_{1}$ = O(ξ n+1) and
$ {\check g}_{1}$ = O(ξ n+1) and ![]() $ {\check g}_{2}$ = O(ξ n+2), which are neglected magnitudes. For the polynomial law,
$ {\check g}_{2}$ = O(ξ n+2), which are neglected magnitudes. For the polynomial law,
from which
 $$ \eqalign{ {\check g}_{1}( \xi,Z, {\bar t}) & = {{\displaystyle{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) \{[ {\check H}(\xi, {\bar t})]^2 \cr & - [ {\check H}(\xi, {\bar t}) - Z]^2\} + O(\xi^3),} $$
$$ \eqalign{ {\check g}_{1}( \xi,Z, {\bar t}) & = {{\displaystyle{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) \{[ {\check H}(\xi, {\bar t})]^2 \cr & - [ {\check H}(\xi, {\bar t}) - Z]^2\} + O(\xi^3),} $$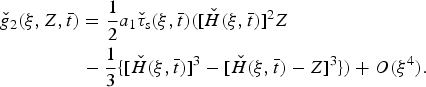 $$ \eqalign{{\check g}_{2}( \xi,Z, {\bar t}) & = \displaystyle{{{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) ([ {\check H}(\xi, {\bar t})]^{2}Z \cr & - \displaystyle{{1} \over {3}} \{[ {\check H}(\xi, {\bar t})]^{3}- [ {\check H} (\xi, {\bar t})-Z]^3\}) +O(\xi^4).} $$
$$ \eqalign{{\check g}_{2}( \xi,Z, {\bar t}) & = \displaystyle{{{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) ([ {\check H}(\xi, {\bar t})]^{2}Z \cr & - \displaystyle{{1} \over {3}} \{[ {\check H}(\xi, {\bar t})]^{3}- [ {\check H} (\xi, {\bar t})-Z]^3\}) +O(\xi^4).} $$ Hence, by (19), for the power law ![]() $ {\check U}(\xi ,\,Z,\, {\bar t}) = {\check U}_{{\rm b}}(\xi ,\, {\bar t})$ neglecting terms of order ξ n+1, which is independent of Z. This was deduced by Nye (Reference Nye2015) for the flow very close to the terminus, but the theoretical prediction shown in his Figure 4, reinforced by his comment in the text, implies a significant Z dependence further away, though still within the small ξ range corresponding to Glen (Reference Glen1961)'s measurements. That is, the actual flow solution is different from Nye (Reference Nye2015)'s approximate solution, independent of the measured data. For the polynomial law there is a Z dependence arising from
$ {\check U}(\xi ,\,Z,\, {\bar t}) = {\check U}_{{\rm b}}(\xi ,\, {\bar t})$ neglecting terms of order ξ n+1, which is independent of Z. This was deduced by Nye (Reference Nye2015) for the flow very close to the terminus, but the theoretical prediction shown in his Figure 4, reinforced by his comment in the text, implies a significant Z dependence further away, though still within the small ξ range corresponding to Glen (Reference Glen1961)'s measurements. That is, the actual flow solution is different from Nye (Reference Nye2015)'s approximate solution, independent of the measured data. For the polynomial law there is a Z dependence arising from ![]() $ {\check g}_{1}( \xi ,\,Z,\, {\bar t})$, but this is small, of order ξ 2. Thus, the longitudinal velocity for both laws, neglecting order ξ 3, is expressed by
$ {\check g}_{1}( \xi ,\,Z,\, {\bar t})$, but this is small, of order ξ 2. Thus, the longitudinal velocity for both laws, neglecting order ξ 3, is expressed by
 $$ \eqalign{&{\check U}(\xi,Z, {\bar t}) = {\check U}_{{\rm b}}(\xi, {\bar t}) + K(\xi, {\bar t}), \cr & K(\xi, {\bar t}) = {\displaystyle{{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) \left\{[ {\check H}(\xi, {\bar t})]^2 - [ {\check H}(\xi, {\bar t})- Z]^2\right\},} $$
$$ \eqalign{&{\check U}(\xi,Z, {\bar t}) = {\check U}_{{\rm b}}(\xi, {\bar t}) + K(\xi, {\bar t}), \cr & K(\xi, {\bar t}) = {\displaystyle{{1} \over {2}}} a_{1} {\check \tau}_{{\rm s}}(\xi, {\bar t}) \left\{[ {\check H}(\xi, {\bar t})]^2 - [ {\check H}(\xi, {\bar t})- Z]^2\right\},} $$where a 1 is zero for the power law, and is given by (29) for the polynomial law.
The later illustration will use Glen (Reference Glen1961)'s data which includes the down-surface velocity (the variation of the velocity at the surface, parallel to the surface), v s(x G) at time ![]() $ {\bar t} = 0$, where x G is the distance along the curved surface. This interpretation, instead of the horizontal distance stated in a Figure caption, was advised by both Nye and Glen (personal communications). In dimensionless form
$ {\bar t} = 0$, where x G is the distance along the curved surface. This interpretation, instead of the horizontal distance stated in a Figure caption, was advised by both Nye and Glen (personal communications). In dimensionless form
where ![]() $ {\check {V}}_{\rm s}(\xi )$ can be approximated by an expansion
$ {\check {V}}_{\rm s}(\xi )$ can be approximated by an expansion
with the coefficients V 0, V 1 and V 2 determined by correlation with surface velocity data. The analysis applies for any such surface velocity data ![]() $ {\check {V}}_{\rm s}(\xi )$.
$ {\check {V}}_{\rm s}(\xi )$.
From (32), neglecting terms of order ε 3,
with a 1 set to zero for the power law. Then by (34) and (35) the basal velocity at time ![]() $ {\bar t} = 0$ is
$ {\bar t} = 0$ is
and in turn the longitudinal velocity at time ![]() $ {\bar t} = 0$ becomes
$ {\bar t} = 0$ becomes
both determined completely by the profile and down-surface velocity data, independent of any basal sliding law. The corresponding longitudinal strain-rate is
 $$ \eqalign{{\check D}_{x x}(\xi,Z,0) & = -V_{1} - 2V_{2}\xi + a_{1} {\check \tau}_{\rm s}(\xi,0)[ {\check H}(\xi,0) - Z] {\check{\Gamma}}(\xi) \cr & + {{\displaystyle{1} \over {2}}} a_{1} {\check \tau}_{\rm s}^{\prime}(\xi,0)[ {\check H}(\xi,0) - Z]^2,} $$
$$ \eqalign{{\check D}_{x x}(\xi,Z,0) & = -V_{1} - 2V_{2}\xi + a_{1} {\check \tau}_{\rm s}(\xi,0)[ {\check H}(\xi,0) - Z] {\check{\Gamma}}(\xi) \cr & + {{\displaystyle{1} \over {2}}} a_{1} {\check \tau}_{\rm s}^{\prime}(\xi,0)[ {\check H}(\xi,0) - Z]^2,} $$with the longitudinal deviatoric stress ![]() $ {\check \sigma }_{x x}(\xi ,\,Z,\,0)$ given by the unique inverse of the monotonic relation (6)1. Note that the longitudinal strain-rate is independent of Z for the power law, for which a 1 = 0.
$ {\check \sigma }_{x x}(\xi ,\,Z,\,0)$ given by the unique inverse of the monotonic relation (6)1. Note that the longitudinal strain-rate is independent of Z for the power law, for which a 1 = 0.
Now consider a net melting flux at ![]() $ {\bar t} = 0$ which varies with distance from the terminus, with expansion for small ξ
$ {\bar t} = 0$ which varies with distance from the terminus, with expansion for small ξ
where B 0 > 0 implies melting at the terminus, and apply the expansions to the profile Eqn (23), equating the coefficients of ξ 0, ξ, ξ 2 to obtain the three identities
 $$ \eqalign{& H_{2}^{\prime}(0) + 3H_{3}(0)X_{M}^{\prime}(0) - 3[V_{0}H_{3}(0) + V_{1}H_{2}(0) + V_{2}H_{1}(0) \cr & \quad - {{\displaystyle{1} \over {2}}} a_{1} \kappa\,{cos}\,\chi H_{1}^{3}(0)] = -B_{2}.} $$
$$ \eqalign{& H_{2}^{\prime}(0) + 3H_{3}(0)X_{M}^{\prime}(0) - 3[V_{0}H_{3}(0) + V_{1}H_{2}(0) + V_{2}H_{1}(0) \cr & \quad - {{\displaystyle{1} \over {2}}} a_{1} \kappa\,{cos}\,\chi H_{1}^{3}(0)] = -B_{2}.} $$Immediately, by (40),
which relates the terminus velocity ![]() $ X_{M}^{\prime }(0)$ linearly to the melt flux B 0 at the terminus, and in particular the terminus is retreating if B 0 > V 0H 1(0), which is a positive limit. The terminus can therefore be advancing for some range of positive melt flux. Then (41) and (42) in turn determine
$ X_{M}^{\prime }(0)$ linearly to the melt flux B 0 at the terminus, and in particular the terminus is retreating if B 0 > V 0H 1(0), which is a positive limit. The terminus can therefore be advancing for some range of positive melt flux. Then (41) and (42) in turn determine ![]() $ H_{1}^{\prime }(0)$ in terms of B 1 and
$ H_{1}^{\prime }(0)$ in terms of B 1 and ![]() $H_{2}^{\prime }(0) $ in terms of B 2.
$H_{2}^{\prime }(0) $ in terms of B 2.
In summary, a known profile and down-surface velocity in the terminus vicinity determine the current pressure, the longitudinal velocity, different from Nye (Reference Nye2015)'s approximation and hence the longitudinal deviatoric stress. Given the net melt (or accumulation) in the terminus vicinity, the current terminus velocity and instantaneous rate of change of the profile are determined. In total, a snapshot of the current flow and its rate of change in the terminus vicinity. Note that a solution independent of upstream conditions is possible only because the ice is assumed to be a viscous fluid relating only instantaneous variables, with no memory of its past.
5. AUSTERDALSBREEN ILLUSTRATIONS
The required data for correlation with (26)1 and (34) to determine H 1, H 2, H 3, V 0, V 1, V 2 is given in Glen (Reference Glen1975)'s Table 1. Column 1 labels the stakes where measurements were made, column 2 the distance s G from stake 1 along the ice surface, with s = s G + 5 m an estimate of the distance from the terminus, column 3 is the height (vertical) h G of the surface above stake 1, which, with Nye (Reference Nye2015)'s terminus slope 0.282, implies a height above the horizontal from the terminus of h v = h G + 1.4, and column 4 is the down-surface velocity v s. Neglecting O(ε 3), ![]() $s = (x_M - x)(1 + (1/2)\, {\epsilon }^{2} \gamma _{M}^{2})$ where − γ M is the terminus slope. Adopting Nye (Reference Nye2015)'s approximate surface slope 0.182 relative to the bed gives the approximation s = 1.016(x M − x), so the distance along the x-axis from the terminus is x M − x = 0.984 s. Finally the z surface co-ordinate is h = h v sec χ(x M − x) tan χ = 1.0045 h v − 0.0953 (x M − x). These relations determine the dimensionless co-ordinates
$s = (x_M - x)(1 + (1/2)\, {\epsilon }^{2} \gamma _{M}^{2})$ where − γ M is the terminus slope. Adopting Nye (Reference Nye2015)'s approximate surface slope 0.182 relative to the bed gives the approximation s = 1.016(x M − x), so the distance along the x-axis from the terminus is x M − x = 0.984 s. Finally the z surface co-ordinate is h = h v sec χ(x M − x) tan χ = 1.0045 h v − 0.0953 (x M − x). These relations determine the dimensionless co-ordinates ![]() $\bar {s}$,
$\bar {s}$, ![]() $ {\bar {x}}_M - {\bar {x}}$ and
$ {\bar {x}}_M - {\bar {x}}$ and ![]() $ {\bar {h}}_{v}$, and the dimensionless down-surface velocity
$ {\bar {h}}_{v}$, and the dimensionless down-surface velocity ![]() $ {\bar {v}}_{\rm s}$, then the scaled variables
$ {\bar {v}}_{\rm s}$, then the scaled variables
A common scale factor ε, normalising ξ and ![]() $ {\bar v}_{\rm s}$ for both viscous laws, has been chosen. Table 1 below shows the data expressed in terms of these new variables.
$ {\bar v}_{\rm s}$ for both viscous laws, has been chosen. Table 1 below shows the data expressed in terms of these new variables.
Table 1. Surface profile and velocity data
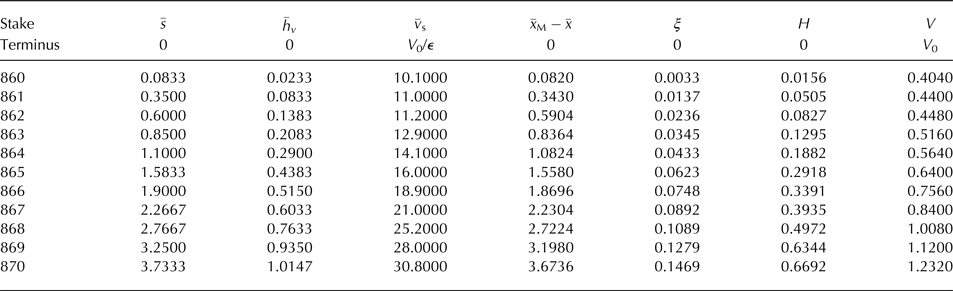
Least squares correlations with the 12 surface data points for linear H(ξ), the constant surface slope approximation adopted by Nye (Reference Nye2015), and for a more accurate cubic H(ξ) adopted in the present analysis, give respectively
with corresponding mean errors 0.0189 and 0.0140. The data points and correlations are shown in Figure 2 in unscaled (dimensionless) variables, with slopes exaggerated by the axes scaling. The linear correlation giving a constant slope ε H 1 = 0.184 is nearly identical to Nye (Reference Nye2015)'s 0.182 approximation. While both correlations have similar error magnitudes, the corresponding surface slopes shown in Figure 3 reveal that the non-constant surface slope for the cubic correlation varies significantly from the constant slope of the linear correlation since the cubic correlation is able to correlate with data points both under and above the constant slope correlation.
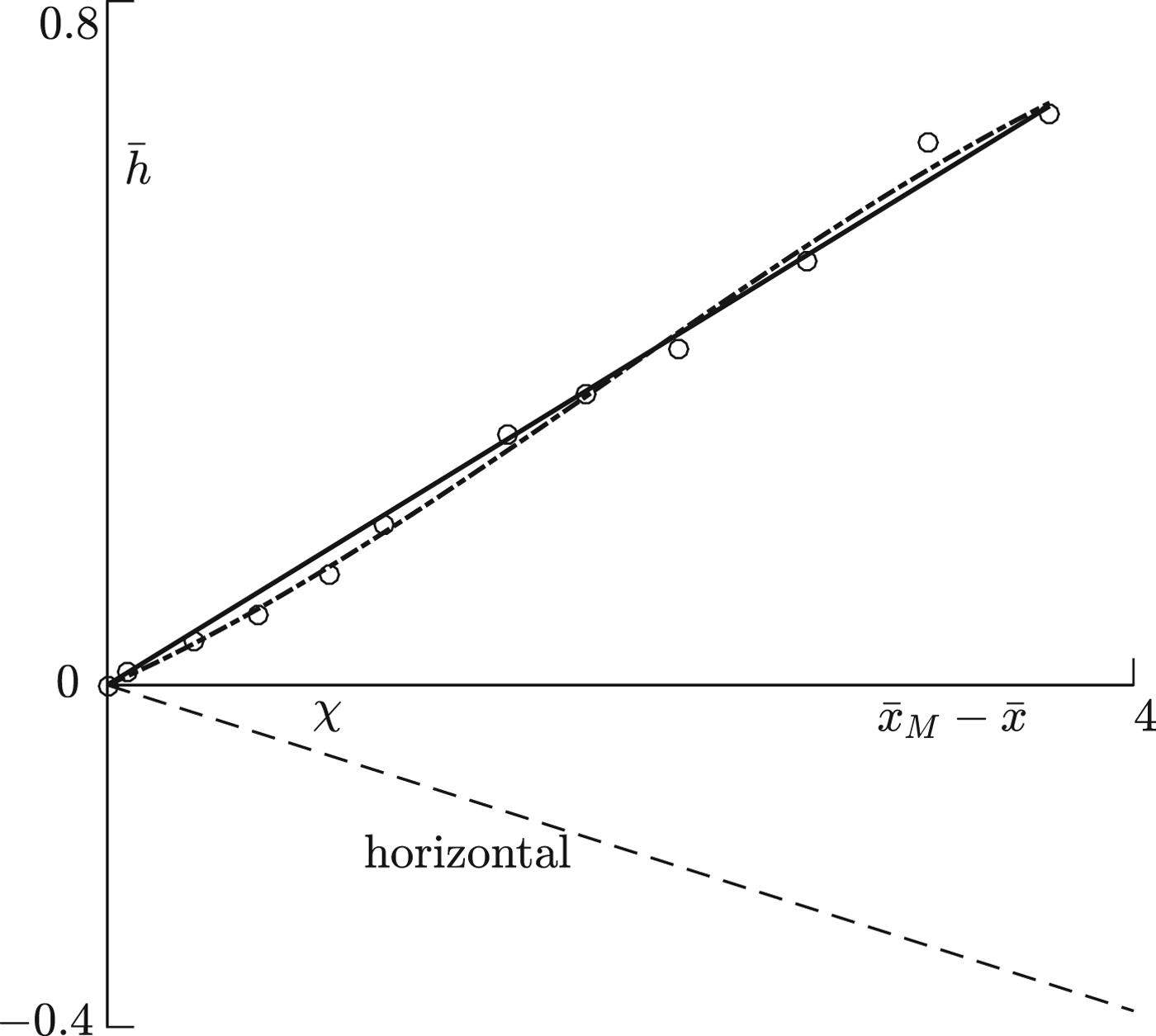
Fig. 2. Profile (circles) data at ![]() $ {\bar t} = 0$ with linear (solid line) and cubic (dash-dot line) correlations. Horizontal inward from terminus shown as dashed line. Slopes exaggerated by axes scaling.
$ {\bar t} = 0$ with linear (solid line) and cubic (dash-dot line) correlations. Horizontal inward from terminus shown as dashed line. Slopes exaggerated by axes scaling.
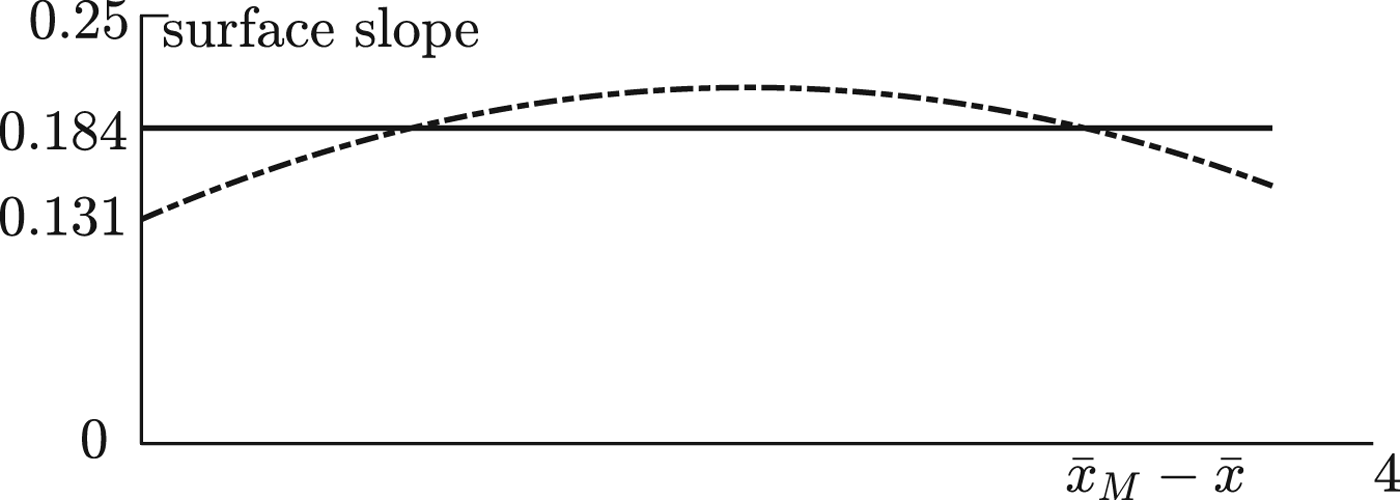
Fig. 3. Linear (solid line) and cubic (dash-dot line) correlation slopes.

Fig. 4. Down-surface velocity data (circles) at ![]() $ {\bar t} = 0$ with linear (solid line) and quadratic (dash-dot line) correlations.
$ {\bar t} = 0$ with linear (solid line) and quadratic (dash-dot line) correlations.
However, these correlations are for data assumed accurate, but realistically there are significant data errors. In particular, Nye (Reference Nye2015) notes that the bed here assumed of constant slope, increases in the upper half of the measurement region, and he has suggested that depth measurements become less accurate moving away from the terminus. The presented illustration assumes accurate data points.
The linear and quadratic correlations for the 11 down-surface velocity points give respectively
with corresponding mean errors 0.0330 and 0.0205. Figure 4 shows the down-surface velocity ![]() $ {\bar v}_{\rm s}$ data points and correlations in unscaled dimensionless variables, and while both correlations have similar error magnitudes, the quadratic correlation matches closely the points both under and over the linear correlation. The velocity at the terminus is approximately 8.1 m a−1. Figure 5 shows the corresponding longitudinal strain-rates
$ {\bar v}_{\rm s}$ data points and correlations in unscaled dimensionless variables, and while both correlations have similar error magnitudes, the quadratic correlation matches closely the points both under and over the linear correlation. The velocity at the terminus is approximately 8.1 m a−1. Figure 5 shows the corresponding longitudinal strain-rates ![]() $-\partial \,v_{\rm s}/\partial \, {\bar {x}}$. The constant strain-rate −∂v s/∂x = 6.043/60 = 1.067 a−1 with the linear correlation corresponds to Nye (Reference Nye2015)'s constant r 0 approximation, though he estimates this to be 0.064 a−1. In fact his estimate is very close to the terminus value of the quadratic approximation 3.94/60 = 0.066 a−1. Again, the more accurate quadratic correlation shows a significant variation from the constant strain-rate correlation. From (40),
$-\partial \,v_{\rm s}/\partial \, {\bar {x}}$. The constant strain-rate −∂v s/∂x = 6.043/60 = 1.067 a−1 with the linear correlation corresponds to Nye (Reference Nye2015)'s constant r 0 approximation, though he estimates this to be 0.064 a−1. In fact his estimate is very close to the terminus value of the quadratic approximation 3.94/60 = 0.066 a−1. Again, the more accurate quadratic correlation shows a significant variation from the constant strain-rate correlation. From (40),
for the constant slope and quadratic slope correlations respectively, giving retreat/advance flux limits B 0 = 1.4622 and B 0 = 1.2158 m a−1.
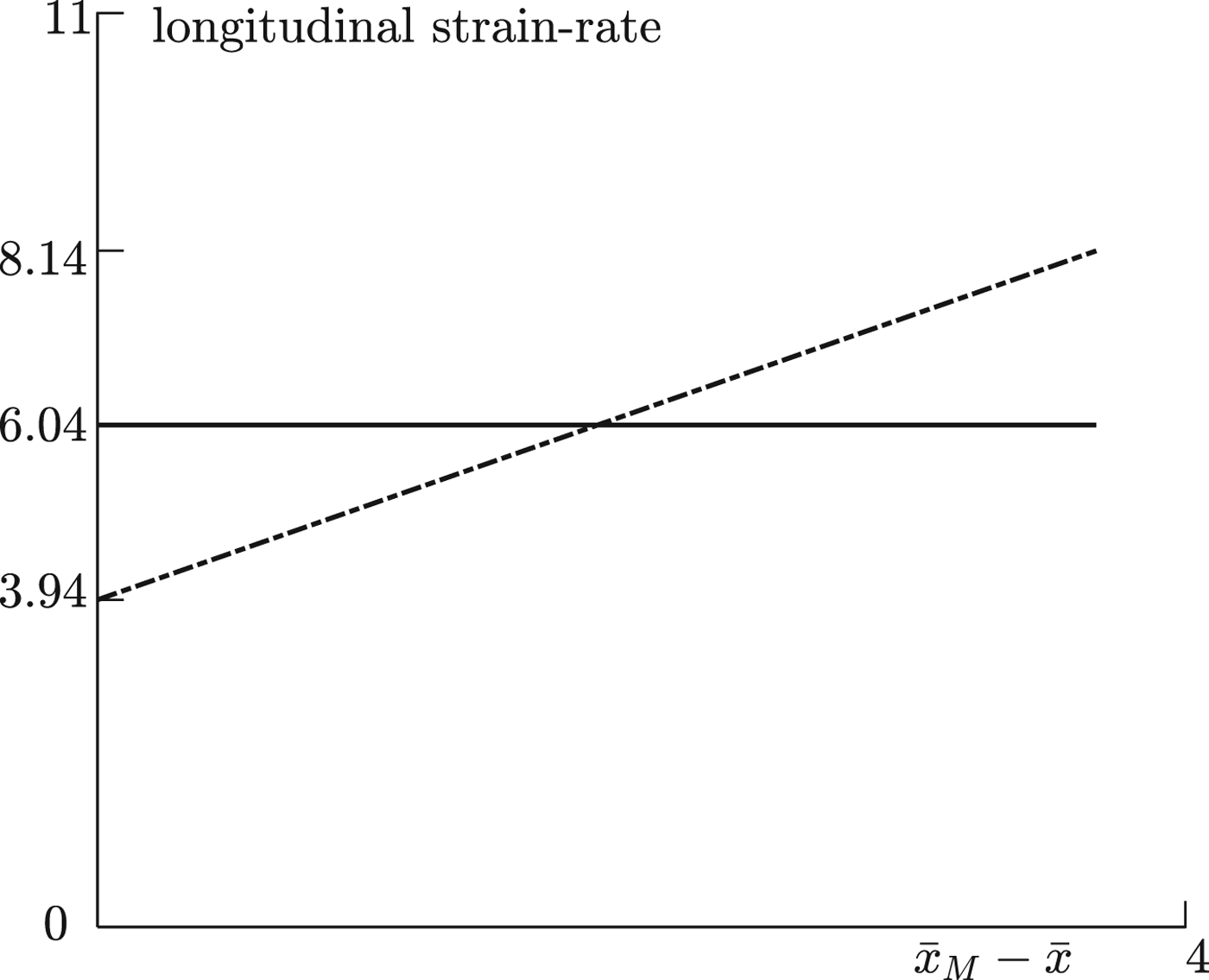
Fig. 5. Linear( solid line) and quadratic (dash-dot line) correlation longitudinal velocity gradients ![]() $\partial \,\bar {v}_{\rm s}/\partial \,\bar {x}$.
$\partial \,\bar {v}_{\rm s}/\partial \,\bar {x}$.
6. CONCLUSIONS
An asymptotic analysis of the unsteady flow in a glacier terminus vicinity based on the reduced model for small surface and bed slopes has shown that surface profile and down-surface velocity data at an observation time determine the longitudinal velocity independent of basal sliding and melt or accumulation boundary conditions. The resulting longitudinal strain-rate and deviatoric stress determined at that time impose a restriction on any basal sliding law, independent of the melt condition. In addition, the terminus velocity and the current rate of change of the surface profile are determined in terms of the melt/accumulation flux. However, since different profile and velocity correlations with errors of similar magnitude show significant differences in slope and velocity gradient, it must follow that errors in data points, which would change the correlations, could also yield significant differences. The present analysis determines accurate solutions for the given data.
One conclusion, independent of the data, is that the longitudinal velocity given by (37) shows negligible depth variation for the viscous power law, in contrast to Nye (Reference Nye2015)'s prediction of significant depth variation, and only small depth variation for the viscous polynomial law.
Illustrations are presented with the linear and cubic correlations of surface profile data, and linear and quadratic correlations of the velocity data, for Austerdalsbreen (Glen, Reference Glen1961).
ACKNOWLEDGEMENTS
This investigation was prompted by Professor Nye who sent me a pre-publication copy of his paper utilising Dr Glen's Austerdalsbreen measurements, and I appreciate his continued interaction as I pursued this asymptotic analysis. Dr Glen kindly found me a copy of the basic paper, and has regularly responded to my queries.










