1 Introduction
Imagine a voting system with yes/no options, for example, direct democracy, indirect democracy, or dictatorship. How much information of the votes do we need until we can conclude the outcome of the election? For dictatorship, we only need the information of the dictator as he or she has all the power, but for a democratic majority we need at least half the votes. Depending on the order in which we find out what the votes are we might need all of them before we can conclude the result. More generally, this question is about complexity of Boolean functions which is application area of this paper.
Boolean functions are widespread in mathematics and computer science and can describe yes-no voter systems, hardware circuits, and predicates (Knuth, Reference Knuth2012; O’Donnell, Reference O’Donnell2014). A Boolean function is a function from
![]() ${\mathit{n}}$
bits to one bit, for example, majority (
${\mathit{n}}$
bits to one bit, for example, majority (
![]() ${\mathit{maj}_{\mathit{n}}}$
), which returns the value that has majority among the
${\mathit{maj}_{\mathit{n}}}$
), which returns the value that has majority among the
![]() ${\mathit{n}}$
inputs. In the context of voting systems, the next subsection gives an example of a Boolean function called iterated majority.
${\mathit{n}}$
inputs. In the context of voting systems, the next subsection gives an example of a Boolean function called iterated majority.
1.1 Vote counting example: iterated majority
In US elections, a presidential candidate can lose even if they win the popular vote. One reason for this is that the outcome is not directly determined by the majority, but rather majority iterated two times.Footnote 1 Our running example is a very much simplified case: consider 3 states with 3 voters in each.

We first compute the majority
![]() $m_i$
in each “state”, and then the majority of
$m_i$
in each “state”, and then the majority of
![]() $m_0$
,
$m_0$
,
![]() $m_1$
, and
$m_1$
, and
![]() $m_2$
. For example we see below
$m_2$
. For example we see below
![]() ${\mathbf{0}}$
,
${\mathbf{0}}$
,
![]() ${\mathbf{1}}$
,
${\mathbf{1}}$
,
![]() ${\mathbf{0}}$
which gives
${\mathbf{0}}$
which gives
![]() $m_0 = {\mathbf{0}}$
, then
$m_0 = {\mathbf{0}}$
, then
![]() ${\mathbf{1}}, {\mathbf{0}}, {\mathbf{1}}$
which gives
${\mathbf{1}}, {\mathbf{0}}, {\mathbf{1}}$
which gives
![]() $m_1 = {\mathbf{1}}$
, and
$m_1 = {\mathbf{1}}$
, and
![]() ${\mathbf{0}}, {\mathbf{1}}, {\mathbf{0}}$
again which gives
${\mathbf{0}}, {\mathbf{1}}, {\mathbf{0}}$
again which gives
![]() $m_2 = {\mathbf{0}}$
. The final majority is
$m_2 = {\mathbf{0}}$
. The final majority is
![]() ${\mathbf{0}}$
:
${\mathbf{0}}$
:

But if we switch the first and 8th bit (perhaps through gerrymandering) we get another result (with the changed bits underlined and marked in red):

This changes
![]() $m_0$
from
$m_0$
from
![]() ${\mathbf{0}}{}$
to
${\mathbf{0}}{}$
to
![]() ${\mathbf{1}}{}$
without affecting
${\mathbf{1}}{}$
without affecting
![]() $m_1$
, or
$m_1$
, or
![]() $m_2$
. But now the two-level majority is changed to
$m_2$
. But now the two-level majority is changed to
![]() ${\mathbf{1}}$
, just from the switch of two bits. Both examples have four
${\mathbf{1}}$
, just from the switch of two bits. Both examples have four
![]() ${\mathbf{1}}{}$
’s and five
${\mathbf{1}}{}$
’s and five
![]() ${\mathbf{0}}{}$
’s but the result is different based on the positioning of the bits. In our case the two-level majority is
${\mathbf{0}}{}$
’s but the result is different based on the positioning of the bits. In our case the two-level majority is
![]() ${\mathbf{1}}{}$
even though there are fewer
${\mathbf{1}}{}$
even though there are fewer
![]() ${\mathbf{1}}{}$
’s than
${\mathbf{1}}{}$
’s than
![]() ${\mathbf{0}}$
’s. This means that the
${\mathbf{0}}$
’s. This means that the
![]() ${\mathbf{0}}{}$
’s “lose” even though they won the “popular vote”.
${\mathbf{0}}{}$
’s “lose” even though they won the “popular vote”.
1.2 Cost and complexity
The field of computational complexity is about “how much” computation is necessary and sufficient to perform certain computational tasks. For example, given a computational problem it tries to establish tight upper and lower bounds on the length of the computation (or on other resources, like space). Unfortunately, for many practically relevant computational problems no tight bounds are known. In our case we study one of the simplest models of computation: the decision tree. We are interested in the cost of evaluating Boolean functions, and we use binary decision trees to describe the evaluation order of Boolean functions. The depth of the decision tree corresponds to the number of votes needed to know the outcome for certain. This is called deterministic complexity. Another well-known notion is randomized complexity, and the randomized complexity bounds of iterated majority have been studied in Landau et al. (Reference Landau, Nachmias, Peres and Vanniasegaram2006), Leonardos (Reference Leonardos2013), and Magniez et al. (Reference Magniez, Nayak, Santha, Sherman, Tardos and Xiao2016). Iterated majority on two levels corresponds to the Boolean function for US elections as described above. We are particularly interested in this function due to its symmetry and simplicity, but still the complexity is non-trivial.
Diving into the literature for complexity of Boolean functions we find many different measures. Relevant concepts are certificate complexity, degree of a Boolean function, and communication complexity (Buhrman & De Wolf, Reference Buhrman and De Wolf2002). Complexity measures related specifically to circuits are circuit complexity, additive, and multiplicative complexity (Wegener, Reference Wegener1987). Considering Boolean computation in practice we have combinational complexity which is the length of the shortest Boolean chain computing it (Knuth, Reference Knuth2012). Thus, there are many competing complexity measures, but we focus on level-
![]() ${\mathit{p}}$
-complexity — a function of the probability p that a bit is
${\mathit{p}}$
-complexity — a function of the probability p that a bit is
![]() ${\mathbf{1}}$
(Garban & Steif, Reference Garban and Steif2014). We assume that the bits are independent and identically Bernoulli-distributed with parameter
${\mathbf{1}}$
(Garban & Steif, Reference Garban and Steif2014). We assume that the bits are independent and identically Bernoulli-distributed with parameter
![]() $p \in [0,1]$
. Then, for each Boolean function
$p \in [0,1]$
. Then, for each Boolean function
![]() ${\mathit{f}}$
and probability
${\mathit{f}}$
and probability
![]() ${\mathit{p}}$
, we get the level-
${\mathit{p}}$
, we get the level-
![]() ${\mathit{p}}$
-complexity by minimizing the expected cost over all decision trees. The level-
${\mathit{p}}$
-complexity by minimizing the expected cost over all decision trees. The level-
![]() ${\mathit{p}}$
-complexity is a piecewise polynomial function of
${\mathit{p}}$
-complexity is a piecewise polynomial function of
![]() ${\mathit{p}}$
and has many interesting properties (Jansson, Reference Jansson2022).
${\mathit{p}}$
and has many interesting properties (Jansson, Reference Jansson2022).
1.3 Contributions
This paper presents a purely functional library for computing level-
![]() ${\mathit{p}}$
-complexity of Boolean functions in general and for
${\mathit{p}}$
-complexity of Boolean functions in general and for
![]() ${\mathit{maj}_{3}^2}$
in particular. The level-
${\mathit{maj}_{3}^2}$
in particular. The level-
![]() ${\mathit{p}}$
-complexity of
${\mathit{p}}$
-complexity of
![]() ${\mathit{maj}_{3}^2}$
was conjectured in Jansson (Reference Jansson2022), but could not be proven because it was hard to generate all possible decision trees. This paper fills that gap by showing that the conjecture is false and by computing the true level-
${\mathit{maj}_{3}^2}$
was conjectured in Jansson (Reference Jansson2022), but could not be proven because it was hard to generate all possible decision trees. This paper fills that gap by showing that the conjecture is false and by computing the true level-
![]() ${\mathit{p}}$
-complexity of
${\mathit{p}}$
-complexity of
![]() ${\mathit{maj}_{3}^2}$
.
${\mathit{maj}_{3}^2}$
.
The strength of our implementation is that it can calculate the level-p-complexity for Boolean functions quickly and correctly, compared to tedious calculations by hand. Our specification uses exhaustive search and considers all possible candidates (decision trees). Some partial candidates dominate (many) others, which may be discarded. Thinning (Bird & Gibbons, Reference Bird and Gibbons2020) is an algorithmic design technique which maintains a small set of partial candidates which provably dominate all other candidates. We hope that one contribution of this paper is an interesting example of how a combination of algorithmic techniques can be used to make the intractable tractable. The code in this paper is available on GitHubFootnote 2 and uses packages from Jansson et al. (Reference Jansson, Ionescu and Bernardy2022). The implementation is in Haskell but should work also in other languages, and parts of it has been reproduced in Agda to check some of the stronger invariants. The choice of Haskell for the implementation is due to its strong compiler and the availability of libraries for BDDs, memoization, and polynomials.
1.4 Motivation
To give the flavor of the end result, we start with two examples which will be explained in detail later: the level-
![]() ${\mathit{p}}$
-complexity of 2-level iterated majority
${\mathit{p}}$
-complexity of 2-level iterated majority
![]() ${\mathit{maj}_{3}^2}$
and of a 5-bit function we call
${\mathit{maj}_{3}^2}$
and of a 5-bit function we call
![]() ${\mathit{sim}_{5}}$
, defined in Figure 1. The level-p-complexity is a piecewise polynomial function of the probability
${\mathit{sim}_{5}}$
, defined in Figure 1. The level-p-complexity is a piecewise polynomial function of the probability
![]() ${\mathit{p}}$
and
${\mathit{p}}$
and
![]() ${\mathit{sim}_{5}}$
is the smallest arity Boolean function we have found which has more than one polynomial piece contributing to the complexity. Polynomials are represented by their coefficients: for example,
${\mathit{sim}_{5}}$
is the smallest arity Boolean function we have found which has more than one polynomial piece contributing to the complexity. Polynomials are represented by their coefficients: for example,
![]() ${\mathit{P}\;[\mskip1.5mu \mathrm{5},\mathbin{-}\mathrm{8},\mathrm{8}\mskip1.5mu]}$
represents
${\mathit{P}\;[\mskip1.5mu \mathrm{5},\mathbin{-}\mathrm{8},\mathrm{8}\mskip1.5mu]}$
represents
![]() $5-8x+8x^2$
. The function
$5-8x+8x^2$
. The function
![]() ${\mathit{genAlgThinMemo}}$
uses thinning and memoization to generate a set of minimal cost polynomials.
${\mathit{genAlgThinMemo}}$
uses thinning and memoization to generate a set of minimal cost polynomials.


Fig. 1. The four polynomials computed by
![]() ${\mathit{genAlgThinMemo}\;\mathrm{5}\;\mathit{sim}_{5}}$
.
${\mathit{genAlgThinMemo}\;\mathrm{5}\;\mathit{sim}_{5}}$
.
The graph, in Figure 1, shows that different polynomials dominate in different intervals. The polynomial
![]() ${\mathit{P}_{1}}$
is best near the end points, but
${\mathit{P}_{1}}$
is best near the end points, but
![]() ${\mathit{P}_{4}}$
is best near
${\mathit{P}_{4}}$
is best near
![]() ${\mathit{p}\mathrel{=}{1}/{2}}$
(despite being really bad near the end points). The level-
${\mathit{p}\mathrel{=}{1}/{2}}$
(despite being really bad near the end points). The level-
![]() ${\mathit{p}}$
-complexity is the piecewise polynomial minimum, a combination of
${\mathit{p}}$
-complexity is the piecewise polynomial minimum, a combination of
![]() ${\mathit{P}_{1}}$
and
${\mathit{P}_{1}}$
and
![]() ${\mathit{P}_{4}}$
. This computation can be done by exhaustive search over the
${\mathit{P}_{4}}$
. This computation can be done by exhaustive search over the
![]() ${\mathrm{54192}}$
different decision trees and
${\mathrm{54192}}$
different decision trees and
![]() ${\mathrm{39}}$
resulting polynomials, but for more complex Boolean functions the doubly exponential growth makes that impractical.
${\mathrm{39}}$
resulting polynomials, but for more complex Boolean functions the doubly exponential growth makes that impractical.
For our running example,
![]() ${\mathit{maj}_{3}^2}$
, a crude estimate indicates we would have
${\mathit{maj}_{3}^2}$
, a crude estimate indicates we would have
![]() $10^{111}$
decision trees to search and very many polynomials. Thus, the computation would be intractable if it were not for the combination of thinning, memoization, and symbolic comparison of polynomials. Thanks to symmetries in the problem there turns out to be just one dominating polynomial, called
$10^{111}$
decision trees to search and very many polynomials. Thus, the computation would be intractable if it were not for the combination of thinning, memoization, and symbolic comparison of polynomials. Thanks to symmetries in the problem there turns out to be just one dominating polynomial, called
![]() $P_*$
in Figure 2, computed by:
$P_*$
in Figure 2, computed by:

Fig. 2. Expected costs of the two different decision trees. Because they are very close we also show their difference in Figure 3.
The graph in Figure 2, shows that only 4 bits are needed in the limiting cases of
![]() ${\mathit{p}\mathrel{=}\mathrm{0}}$
or
${\mathit{p}\mathrel{=}\mathrm{0}}$
or
![]() $ {\mathrm{1}}$
and that just over 6 bits are needed in the maximum at
$ {\mathrm{1}}$
and that just over 6 bits are needed in the maximum at
![]() ${\mathit{p}\mathrel{=}{1}/{2}}$
. Figure 2 also shows the conjectured complexity polynomial
${\mathit{p}\mathrel{=}{1}/{2}}$
. Figure 2 also shows the conjectured complexity polynomial
![]() $P_t$
from Jansson (Reference Jansson2022), and Figure 3 shows the (small) difference between the two polynomials.
$P_t$
from Jansson (Reference Jansson2022), and Figure 3 shows the (small) difference between the two polynomials.

Fig. 3. Difference between the conjectured (
![]() $P_t$
) and the true (
$P_t$
) and the true (
![]() $P_*$
) complexity of
$P_*$
) complexity of
![]() $\mathit{maj}_3^2$
.
$\mathit{maj}_3^2$
.
2 Background
To explain what level-
![]() ${\mathit{p}}$
-complexity of Boolean functions means, we introduce some background about Boolean functions, decision trees, cost, and complexity. The Boolean input type
${\mathit{p}}$
-complexity of Boolean functions means, we introduce some background about Boolean functions, decision trees, cost, and complexity. The Boolean input type
![]() ${\mathbb{B}}$
could be
${\mathbb{B}}$
could be
![]() ${\{\mskip1.5mu \mathit{False},\mathit{True}\mskip1.5mu\},\{\mskip1.5mu \mathit{F},\mathit{T}\mskip1.5mu\}}$
or
${\{\mskip1.5mu \mathit{False},\mathit{True}\mskip1.5mu\},\{\mskip1.5mu \mathit{F},\mathit{T}\mskip1.5mu\}}$
or
![]() ${\{\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu\}}$
and from now on we use
${\{\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu\}}$
and from now on we use
![]() ${\mathbf{0}}{}$
for false and
${\mathbf{0}}{}$
for false and
![]() ${\mathbf{1}}{}$
for true in our notation. In the running text, we write
${\mathbf{1}}{}$
for true in our notation. In the running text, we write
![]() ${\mathit{e}\mathop{:}\mathit{t}}$
for “
${\mathit{e}\mathop{:}\mathit{t}}$
for “
![]() ${\mathit{e}}$
has type
${\mathit{e}}$
has type
![]() ${\mathit{t}}$
” which in the quoted Haskell code is written
${\mathit{t}}$
” which in the quoted Haskell code is written
![]() ${\mathit{e}\mathbin{::}\mathit{t}}$
.
${\mathit{e}\mathbin{::}\mathit{t}}$
.
2.1 Boolean functions
A Boolean function
![]() ${\mathit{f}\mathop{:}\mathbb{B}^{\mathit{n}}\,\to\,\mathbb{B}}$
is a function from
${\mathit{f}\mathop{:}\mathbb{B}^{\mathit{n}}\,\to\,\mathbb{B}}$
is a function from
![]() ${\mathit{n}}$
Boolean inputs to one Boolean output. We sometimes write
${\mathit{n}}$
Boolean inputs to one Boolean output. We sometimes write
![]() ${\mathit{BoolFun}\;\mathit{n}}$
for the type
${\mathit{BoolFun}\;\mathit{n}}$
for the type
![]() ${\mathbb{B}^{\mathit{n}}\,\to\,\mathbb{B}}$
. The easiest examples of Boolean functions are the functions
${\mathbb{B}^{\mathit{n}}\,\to\,\mathbb{B}}$
. The easiest examples of Boolean functions are the functions
![]() ${{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
which ignore the
${{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
which ignore the
![]() ${\mathit{n}}$
input bits and return
${\mathit{n}}$
input bits and return
![]() ${\mathit{b}}$
. The usual logical gates like
${\mathit{b}}$
. The usual logical gates like
![]() ${\mathit{and}_{\mathit{n}}}$
and
${\mathit{and}_{\mathit{n}}}$
and
![]() ${\mathit{or}_{\mathit{n}}}$
are very common Boolean functions. Another example is the dictator function (also known as first projection), which is defined as
${\mathit{or}_{\mathit{n}}}$
are very common Boolean functions. Another example is the dictator function (also known as first projection), which is defined as
![]() ${{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;[\mskip1.5mu \mathit{x}_{0},\mathbin{...},\mathit{x}_n\mskip1.5mu]\mathrel{=}\mathit{x}_{0}}$
when the dictator is bit
${{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;[\mskip1.5mu \mathit{x}_{0},\mathbin{...},\mathit{x}_n\mskip1.5mu]\mathrel{=}\mathit{x}_{0}}$
when the dictator is bit
![]() ${\mathrm{0}}$
.
${\mathrm{0}}$
.
A naive representation of a Boolean function could be a pair of an arity and a function
![]() ${\mathit{f}}$
:
${\mathit{f}}$
:
![]() ${[\mskip1.5mu \mathbb{B}\mskip1.5mu]\,\to\,\mathbb{B}}$
, but that turns out to be inefficient when we want to compare and tabulate them (see Section 3.3). Instead we use binary decision diagrams,
${[\mskip1.5mu \mathbb{B}\mskip1.5mu]\,\to\,\mathbb{B}}$
, but that turns out to be inefficient when we want to compare and tabulate them (see Section 3.3). Instead we use binary decision diagrams,
![]() ${\mathit{BDD}}$
s (Bryant, Reference Bryant1986) as implemented in Masahiro Sakai’s excellent Hackage package
Footnote 3
. The package reimplements all the usual Boolean operations on what is semantically expressions in
${\mathit{BDD}}$
s (Bryant, Reference Bryant1986) as implemented in Masahiro Sakai’s excellent Hackage package
Footnote 3
. The package reimplements all the usual Boolean operations on what is semantically expressions in
![]() ${\mathit{n}}$
Boolean variables. BDDs are an efficient way of representing Boolean functions, and they can be used for testing, verification, and complexity analysis. For readability, we will present Boolean functions in the naive representation, but the actual code uses the type
${\mathit{n}}$
Boolean variables. BDDs are an efficient way of representing Boolean functions, and they can be used for testing, verification, and complexity analysis. For readability, we will present Boolean functions in the naive representation, but the actual code uses the type
![]() ${\mathit{BDD}\;\mathit{a}}$
from the
${\mathit{BDD}\;\mathit{a}}$
from the
![]() ${\mathit{BDD}}$
package (where
${\mathit{BDD}}$
package (where
![]() ${\mathit{a}}$
keeps track of variable ordering). Note that we only use BDDs to represent our Boolean functions, not our decision trees.
${\mathit{a}}$
keeps track of variable ordering). Note that we only use BDDs to represent our Boolean functions, not our decision trees.
In the complexity computation, we only need two operations on Boolean functions which we capture in the following type class interface:

The use of a type class here means we keep the interface to the BDD implementation minimal, which makes proofs easier and gives better feedback from the type system. The first method,
![]() ${\mathit{isConst}\;\mathit{f}}$
, returns
${\mathit{isConst}\;\mathit{f}}$
, returns
![]() ${\mathit{Just}\;\mathit{b}}$
iff the function
${\mathit{Just}\;\mathit{b}}$
iff the function
![]() ${\mathit{f}}$
is constant and always returns
${\mathit{f}}$
is constant and always returns
![]() ${\mathit{b}\mathop{:}\mathbb{B}}$
. The second method,
${\mathit{b}\mathop{:}\mathbb{B}}$
. The second method,
![]() ${\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f}}$
, restricts a Boolean function (on
${\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f}}$
, restricts a Boolean function (on
![]() ${\mathit{n}\mathbin{+}\mathrm{1}}$
bits) by setting its
${\mathit{n}\mathbin{+}\mathrm{1}}$
bits) by setting its
![]() ${\mathit{i}}$
th bit to
${\mathit{i}}$
th bit to
![]() ${\mathit{b}}$
. The result is a “subfunction” on the remaining
${\mathit{b}}$
. The result is a “subfunction” on the remaining
![]() ${\mathit{n}}$
bits, abbreviated
${\mathit{n}}$
bits, abbreviated
![]() $f^{i}_{b}$
, and illustrated in Figure 4.
$f^{i}_{b}$
, and illustrated in Figure 4.

Fig. 4. The tree of subfunctions of a Boolean function
![]() ${\mathit{f}}$
. This tree structure is also the call graph for our generation of decision trees. Note that this tree structure is related to, but not the same as, the decision trees.
${\mathit{f}}$
. This tree structure is also the call graph for our generation of decision trees. Note that this tree structure is related to, but not the same as, the decision trees.
As an example, for the function
![]() ${\mathit{and}_{2}}$
we have that
${\mathit{and}_{2}}$
we have that
![]() ${\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{and}_{2}\mathrel{=}{\mathit{const}_{\mathrm{1}}}\;{\mathbf{0}}{}}$
and
${\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{and}_{2}\mathrel{=}{\mathit{const}_{\mathrm{1}}}\;{\mathbf{0}}{}}$
and
![]() ${\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{and}_{2}\mathrel{=}\mathit{id}}$
. For
${\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{and}_{2}\mathrel{=}\mathit{id}}$
. For
![]() ${\mathit{and}_{2}}$
we get the same result for
${\mathit{and}_{2}}$
we get the same result for
![]() ${\mathit{i}\mathrel{=}\mathrm{0}}$
, or
${\mathit{i}\mathrel{=}\mathrm{0}}$
, or
![]() ${\mathrm{1}}$
but for the dictator function it depends if we pick the dictator index (
${\mathrm{1}}$
but for the dictator function it depends if we pick the dictator index (
![]() ${\mathrm{0}}$
) or not. We get
${\mathrm{0}}$
) or not. We get
![]() ${\mathit{setBit}\;\mathrm{0}\;\mathit{b}\;{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\mathrel{=}{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
, because the result is dictated by bit
${\mathit{setBit}\;\mathrm{0}\;\mathit{b}\;{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\mathrel{=}{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
, because the result is dictated by bit
![]() ${\mathrm{0}}$
. Otherwise, we get
${\mathrm{0}}$
. Otherwise, we get
![]() ${\mathit{setBit}\;(\mathit{i}\mathbin{+}\mathrm{1})\;\mathit{b}\;{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\mathrel{=}{\mathit{dict}_{\mathit{n}}}}$
irrespective of the value of
${\mathit{setBit}\;(\mathit{i}\mathbin{+}\mathrm{1})\;\mathit{b}\;{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}\mathrel{=}{\mathit{dict}_{\mathit{n}}}}$
irrespective of the value of
![]() ${\mathit{b}}$
since only the value of the dictator bit matters. This behavior is shown in Figure 5.
${\mathit{b}}$
since only the value of the dictator bit matters. This behavior is shown in Figure 5.

Fig. 5. The tree of subfunctions of the
![]() ${{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}}$
function.
${{\mathit{dict}_{\mathit{n}\mathbin{+}\mathrm{1}}}}$
function.
2.2 Decision trees
Consider a decision tree that picks the
![]() ${\mathit{n}}$
bits of a Boolean function
${\mathit{n}}$
bits of a Boolean function
![]() ${\mathit{f}}$
in a deterministic way depending on the values of the bits picked further up the tree. Decision trees are referred to as algorithms in Landau et al. (Reference Landau, Nachmias, Peres and Vanniasegaram2006); Garban & Steif (Reference Garban and Steif2014); Jansson (Reference Jansson2022). Given a Boolean function
${\mathit{f}}$
in a deterministic way depending on the values of the bits picked further up the tree. Decision trees are referred to as algorithms in Landau et al. (Reference Landau, Nachmias, Peres and Vanniasegaram2006); Garban & Steif (Reference Garban and Steif2014); Jansson (Reference Jansson2022). Given a Boolean function
![]() ${\mathit{f}}$
, a decision tree
${\mathit{f}}$
, a decision tree
![]() ${\mathit{t}}$
describes one way to evaluate the function
${\mathit{t}}$
describes one way to evaluate the function
![]() ${\mathit{f}}$
. The Haskell datatype is as follows:
${\mathit{f}}$
. The Haskell datatype is as follows:
Parts of the “rules of the game” in the mathematical literature are that you must return a
![]() ${\mathit{Res}}$
ult if the function is constant and you may only
${\mathit{Res}}$
ult if the function is constant and you may only
![]() ${\mathit{Pick}}$
an index once. We can capture most of these rules with a type family version of the
${\mathit{Pick}}$
an index once. We can capture most of these rules with a type family version of the
![]() ${\mathit{DecTree}}$
datatype (here expressed in
${\mathit{DecTree}}$
datatype (here expressed in
![]() ${\mathit{Agda}}$
syntax). Here we use two type indices:
${\mathit{Agda}}$
syntax). Here we use two type indices:
![]() ${\mathit{t}\mathop{:}\mathit{DecTree}\;\mathit{n}\;\mathit{f}}$
is a decision tree for the Boolean function
${\mathit{t}\mathop{:}\mathit{DecTree}\;\mathit{n}\;\mathit{f}}$
is a decision tree for the Boolean function
![]() ${\mathit{f}}$
, of arity
${\mathit{f}}$
, of arity
![]() ${\mathit{n}}$
. The
${\mathit{n}}$
. The
![]() ${\mathit{Res}}$
constructor may only be used for constant functions (but for any arity), while
${\mathit{Res}}$
constructor may only be used for constant functions (but for any arity), while
![]() ${\mathit{Pick}\;\mathit{i}}$
takes two subtrees for Boolean functions of arity
${\mathit{Pick}\;\mathit{i}}$
takes two subtrees for Boolean functions of arity
![]() ${\mathit{n}}$
to a tree of arity
${\mathit{n}}$
to a tree of arity
![]() ${\mathit{suc}\;\mathit{n}\mathrel{=}\mathit{n}\mathbin{+}\mathrm{1}}$
.
${\mathit{suc}\;\mathit{n}\mathrel{=}\mathit{n}\mathbin{+}\mathrm{1}}$
.

Note that the dependently typed version of
![]() ${\mathit{setBit}}$
clearly indicates that the resulting function
${\mathit{setBit}}$
clearly indicates that the resulting function
![]() ${\mathit{g}\mathrel{=}(\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f})\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
has arity one less that of
${\mathit{g}\mathrel{=}(\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f})\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
has arity one less that of
![]() ${\mathit{f}\mathop{:}\mathit{BoolFun}\;(\mathit{suc}\;\mathit{n})}$
. This helps maintaining the invariant that each input bit may only be picked once.
Footnote 4 We use the Haskell versions, but the Agda versions capture the invariants better.
${\mathit{f}\mathop{:}\mathit{BoolFun}\;(\mathit{suc}\;\mathit{n})}$
. This helps maintaining the invariant that each input bit may only be picked once.
Footnote 4 We use the Haskell versions, but the Agda versions capture the invariants better.
We can use these rules backward to generate all possible decision trees for a certain function. If the function is constant, returning
![]() ${\mathit{b}\mathop{:}\mathbb{B}}$
, we immediately know that the only decision tree allowed is
${\mathit{b}\mathop{:}\mathbb{B}}$
, we immediately know that the only decision tree allowed is
![]() ${\mathit{Res}\;\mathit{b}}$
. If it is not constant, we pick any index
${\mathit{Res}\;\mathit{b}}$
. If it is not constant, we pick any index
![]() ${\mathit{i}}$
, any decision tree
${\mathit{i}}$
, any decision tree
![]() ${\mathit{t}_{0}}$
for the subfunction
${\mathit{t}_{0}}$
for the subfunction
![]() ${\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{f}}$
and
${\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{f}}$
and
![]() ${\mathit{t}_{1}}$
for the subfunction
${\mathit{t}_{1}}$
for the subfunction
![]() ${\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{f}}$
recursively. We get back to this in Section 3.1 after some preparation.
${\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{f}}$
recursively. We get back to this in Section 3.1 after some preparation.
Note that we do not use binary decision diagrams (BDDs) to represent our decision trees. An example of a decision tree for the majority function
![]() ${\mathit{maj}_{3}}$
on three bits is defined by the expression
${\mathit{maj}_{3}}$
on three bits is defined by the expression
![]() ${\mathit{ex1}}$
visualised in Figure 6.
${\mathit{ex1}}$
visualised in Figure 6.

Fig. 6. An example of a decision tree for
![]() ${\mathit{maj}_{3}}$
. The root node branches on the value of bit 0. If it is
${\mathit{maj}_{3}}$
. The root node branches on the value of bit 0. If it is
![]() ${\mathbf{0}}$
, it picks bit 2, while if it is
${\mathbf{0}}$
, it picks bit 2, while if it is
![]() ${\mathbf{1}}$
, it picks bit 1. It then picks the last remaining bit if necessary.
${\mathbf{1}}$
, it picks bit 1. It then picks the last remaining bit if necessary.
We will define several functions as folds over
![]() ${\mathit{DecTree}}$
and to do that we introduce a type class
${\mathit{DecTree}}$
and to do that we introduce a type class
![]() ${\mathit{TreeAlg}}$
(for “Tree Algebra”) which collects the two methods
${\mathit{TreeAlg}}$
(for “Tree Algebra”) which collects the two methods
![]() ${\mathit{res}}$
and
${\mathit{res}}$
and
![]() ${\mathit{pic}}$
which are then used in the fold to replace the constructors
${\mathit{pic}}$
which are then used in the fold to replace the constructors
![]() ${\mathit{Res}}$
and
${\mathit{Res}}$
and
![]() ${\mathit{Pick}}$
.
${\mathit{Pick}}$
.

The
![]() ${\mathit{TreeAlg}}$
class is used to define our decision trees but also for several other purposes. (In the implementation, we additionally require some total order on
${\mathit{TreeAlg}}$
class is used to define our decision trees but also for several other purposes. (In the implementation, we additionally require some total order on
![]() ${\mathit{a}}$
to enable efficient set computations.) We see that our decision tree type is the initial algebra of
${\mathit{a}}$
to enable efficient set computations.) We see that our decision tree type is the initial algebra of
![]() ${\mathit{TreeAlg}}$
and that we can reimplement a generic version of
${\mathit{TreeAlg}}$
and that we can reimplement a generic version of
![]() ${\mathit{ex1}}$
which can be instantiated to any
${\mathit{ex1}}$
which can be instantiated to any
![]() ${\mathit{TreeAlg}}$
instance:
${\mathit{TreeAlg}}$
instance:

2.3 Expected cost
For a function
![]() ${\mathit{f}}$
and a specific input
${\mathit{f}}$
and a specific input
![]() ${\mathit{xs}\mathop{:}\mathbb{B}^{\mathit{n}}}$
, the cost of evaluating
${\mathit{xs}\mathop{:}\mathbb{B}^{\mathit{n}}}$
, the cost of evaluating
![]() ${\mathit{f}}$
according to a decision tree
${\mathit{f}}$
according to a decision tree
![]() ${\mathit{t}}$
is the length of the path from root to leaf dictated by the bits in
${\mathit{t}}$
is the length of the path from root to leaf dictated by the bits in
![]() ${\mathit{xs}}$
. We then let the bits be independent and identically distributed with probability
${\mathit{xs}}$
. We then let the bits be independent and identically distributed with probability
![]() $p \in [0,1]$
for
$p \in [0,1]$
for
![]() ${{\mathbf{1}}{}}$
and compute the expected cost (averaging over all
${{\mathbf{1}}{}}$
and compute the expected cost (averaging over all
![]() $2^n$
inputs). Expected cost can be implemented as an instance of
$2^n$
inputs). Expected cost can be implemented as an instance of
![]() ${\mathit{TreeAlg}}$
.
${\mathit{TreeAlg}}$
.

Note that the expected cost of any decision tree for a Boolean function of
![]() ${\mathit{n}}$
bits will always be a polynomial. We represent polynomials as lists of coefficients:
${\mathit{n}}$
bits will always be a polynomial. We represent polynomials as lists of coefficients:
![]() ${\mathit{P}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]}$
represents
${\mathit{P}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]}$
represents
![]() ${\lambda \mathit{p}\,\to\,\mathrm{1}\mathbin{+}\mathrm{2}\times\mathit{p}\mathbin{+}\mathrm{3}\times{\mathit{p}^{\mathrm{2}}}}$
and use
${\lambda \mathit{p}\,\to\,\mathrm{1}\mathbin{+}\mathrm{2}\times\mathit{p}\mathbin{+}\mathrm{3}\times{\mathit{p}^{\mathrm{2}}}}$
and use
![]() ${\mathit{evalP}\mathop{:}\mathit{Ring}\;\mathit{a}\Rightarrow \mathit{Poly}\;\mathit{a}\,\to\,(\mathit{a}\,\to\,\mathit{a})}$
to evaluate polynomials. The polynomial implementation borrowed from Jansson et al. (Reference Jansson, Ionescu and Bernardy2022) includes the polynomial ring operations (
${\mathit{evalP}\mathop{:}\mathit{Ring}\;\mathit{a}\Rightarrow \mathit{Poly}\;\mathit{a}\,\to\,(\mathit{a}\,\to\,\mathit{a})}$
to evaluate polynomials. The polynomial implementation borrowed from Jansson et al. (Reference Jansson, Ionescu and Bernardy2022) includes the polynomial ring operations (
![]() ${(\mathbin{+})}$
,
${(\mathbin{+})}$
,
![]() ${(\mathbin{-})}$
,
${(\mathbin{-})}$
,
![]() ${(\times)}$
),
${(\times)}$
),
![]() ${\mathit{gcd}}$
,
${\mathit{gcd}}$
,
![]() ${\mathit{divMod}}$
, symbolic derivative, and ordering. The
${\mathit{divMod}}$
, symbolic derivative, and ordering. The
![]() ${\mathit{res}}$
and
${\mathit{res}}$
and
![]() ${\mathit{pic}}$
functions are as follows:
${\mathit{pic}}$
functions are as follows:

Here
![]() ${\mathit{zero}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mskip1.5mu]} and {\mathit{one}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mathrm{1}\mskip1.5mu]} represent {\mathit{const}\;\mathrm{0}}$
and
${\mathit{zero}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mskip1.5mu]} and {\mathit{one}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mathrm{1}\mskip1.5mu]} represent {\mathit{const}\;\mathrm{0}}$
and
![]() ${\mathit{const}\;\mathrm{1}}$
, respectively, while
${\mathit{const}\;\mathrm{1}}$
, respectively, while
![]() ${\mathit{xP}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu]}$
is “the polynomial
${\mathit{xP}\mathrel{=}\mathit{P}\;[\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu]}$
is “the polynomial
![]() ${\mathit{x}}$
”. For
${\mathit{x}}$
”. For
![]() ${\mathit{pickPoly}\;- \;\mathit{q}_{0}\;\mathit{q}_{1}}$
, we first have to pick one bit and then if this bit is
${\mathit{pickPoly}\;- \;\mathit{q}_{0}\;\mathit{q}_{1}}$
, we first have to pick one bit and then if this bit is
![]() ${\mathbf{0}}$
(with probability
${\mathbf{0}}$
(with probability
![]() $\mathbb{P}(x_{i} = {\mathbf{0}}$
) = (1-p)) we get
$\mathbb{P}(x_{i} = {\mathbf{0}}$
) = (1-p)) we get
![]() $q_0$
which is the polynomial for this case. If the bit is instead
$q_0$
which is the polynomial for this case. If the bit is instead
![]() ${\mathbf{1}}$
(with probability
${\mathbf{1}}$
(with probability
![]() $\mathbb{P}(x_{i} = {\mathbf{1}}) = p$
) we get
$\mathbb{P}(x_{i} = {\mathbf{1}}) = p$
) we get
![]() $q_1$
. The expected cost of the decision tree
$q_1$
. The expected cost of the decision tree
![]() ${\mathit{ex1}}$
is
${\mathit{ex1}}$
is
![]() $2 + 2p - 2p^2$
. From now on we will use Haskell’s overloading to write
$2 + 2p - 2p^2$
. From now on we will use Haskell’s overloading to write
![]() ${\mathrm{0}}$
and
${\mathrm{0}}$
and
![]() ${\mathrm{1}}$
for
${\mathrm{1}}$
for
![]() ${\mathit{zero}}$
and
${\mathit{zero}}$
and
![]() ${\mathit{one}}$
even when working with polynomials.
${\mathit{one}}$
even when working with polynomials.
2.4 Complexity
Now that we have introduced expected cost, we can introduce the level-
![]() ${\mathit{p}}$
-complexity
${\mathit{p}}$
-complexity
![]() ${{D_p(\mathit{f})}}$
as the pointwise minimum of the expected cost over all of
${{D_p(\mathit{f})}}$
as the pointwise minimum of the expected cost over all of
![]() ${\mathit{f}}$
’s decision trees:
${\mathit{f}}$
’s decision trees:
where the generation of decision trees is explained in Section 3.1. When minimizing we do not necessarily get a polynomial, but a piecewise polynomial function. For simplicity, we represent a piecewise polynomial function as a set of polynomials:

This representation will be inefficient if the set is big, but as a specification it works fine and we will later use thinning to keep the set small (see Sections 3.2 and 3.4). We say that one polynomial
![]() ${\mathit{q}}$
is “uniformly worse” than another polynomial
${\mathit{q}}$
is “uniformly worse” than another polynomial
![]() ${\mathit{p}}$
when
${\mathit{p}}$
when
![]() ${\mathit{p}\;\mathit{x}{\leqslant} \mathit{q}\;\mathit{x}}$
for all
${\mathit{p}\;\mathit{x}{\leqslant} \mathit{q}\;\mathit{x}}$
for all
![]() ${\mathrm{0}{\leqslant} \mathit{x}{\leqslant} \mathrm{1}}$
and
${\mathrm{0}{\leqslant} \mathit{x}{\leqslant} \mathrm{1}}$
and
![]() ${\mathit{p}\;\mathit{x}\mathbin{<}\mathit{q}\;\mathit{x}}$
for some
${\mathit{p}\;\mathit{x}\mathbin{<}\mathit{q}\;\mathit{x}}$
for some
![]() ${\mathrm{0}\mathbin{<}\mathit{x}\mathbin{<}\mathrm{1}}$
. For some polynomials, we cannot determine which is worse, see Figure 1 where four polynomials all intersect. In this case, they are incomparable.
${\mathrm{0}\mathbin{<}\mathit{x}\mathbin{<}\mathrm{1}}$
. For some polynomials, we cannot determine which is worse, see Figure 1 where four polynomials all intersect. In this case, they are incomparable.
When computing the level-
![]() ${\mathit{p}}$
-complexity, it would be possible to take both
${\mathit{p}}$
-complexity, it would be possible to take both
![]() ${\mathit{f}}$
and the probability
${\mathit{f}}$
and the probability
![]() ${\mathit{p}}$
as arguments and return the smallest expected cost for that probability, but we prefer to just take
${\mathit{p}}$
as arguments and return the smallest expected cost for that probability, but we prefer to just take
![]() ${\mathit{f}}$
as an argument and compute a piecewise polynomial function representation. In this way, we can analyze the result symbolically to find minima, maxima, number of polynomial pieces, etc.
${\mathit{f}}$
as an argument and compute a piecewise polynomial function representation. In this way, we can analyze the result symbolically to find minima, maxima, number of polynomial pieces, etc.
2.5 Examples of Boolean functions and their costs
Now that we have introduced expected cost and level-
![]() ${\mathit{p}}$
-complexity, we give a few examples of Boolean functions and their costs to give a feeling of how the computations work. The impatient reader can skip forward to Section 3. As mentioned earlier (in Section 2.1), we present the Boolean functions as Haskell functions for readability, but every example has a BDD counterpart.
${\mathit{p}}$
-complexity, we give a few examples of Boolean functions and their costs to give a feeling of how the computations work. The impatient reader can skip forward to Section 3. As mentioned earlier (in Section 2.1), we present the Boolean functions as Haskell functions for readability, but every example has a BDD counterpart.
For the constant functions (
![]() ${{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
), there is just one legal decision tree
${{\mathit{const}_{\mathit{n}}}\;\mathit{b}}$
), there is just one legal decision tree
![]() ${\mathit{t}\mathrel{=}\mathit{Res}\;\mathit{b}}$
and thus
${\mathit{t}\mathrel{=}\mathit{Res}\;\mathit{b}}$
and thus
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathrm{0}}$
which gives
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathrm{0}}$
which gives
![]() $D_p({{\mathit{const}_{\mathit{n}}}\;\mathit{b}}) = 0$
. For the dictator function, there are many decision trees, but as we can see in Figure 5, picking bit 0 first is optimal and gets us to the constant case just covered. Thus, the optimal tree is
$D_p({{\mathit{const}_{\mathit{n}}}\;\mathit{b}}) = 0$
. For the dictator function, there are many decision trees, but as we can see in Figure 5, picking bit 0 first is optimal and gets us to the constant case just covered. Thus, the optimal tree is
![]() ${\mathit{optTree}\mathrel{=}\mathit{Pick}\;\mathrm{0}\;(\mathit{Res}\;{\mathbf{0}}{})\;(\mathit{Res}\;{\mathbf{1}}{})}$
, and we can compute the expected cost as follows.
${\mathit{optTree}\mathrel{=}\mathit{Pick}\;\mathrm{0}\;(\mathit{Res}\;{\mathbf{0}}{})\;(\mathit{Res}\;{\mathbf{1}}{})}$
, and we can compute the expected cost as follows.

In this case, all bits have to be picked to determine the parity, regardless of input. We prove that for all decision trees
![]() ${\mathit{t}}$
of
${\mathit{t}}$
of
![]() ${\mathit{par}_{\!\mathit{n}}}$
or
${\mathit{par}_{\!\mathit{n}}}$
or
![]() ${\neg \;\mathit{par}_{\!\mathit{n}}}$
, we have that
${\neg \;\mathit{par}_{\!\mathit{n}}}$
, we have that
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
using induction over
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
using induction over
![]() ${\mathit{n}}$
. For the base case,
${\mathit{n}}$
. For the base case,
![]() ${\mathit{n}\mathrel{=}\mathrm{0}}$
we have that
${\mathit{n}\mathrel{=}\mathrm{0}}$
we have that
![]() ${\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{0}}{}}$
and
${\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{0}}{}}$
and
![]() ${\neg \;\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{1}}{}}$
so that
${\neg \;\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{1}}{}}$
so that
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathrm{0}}$
for all decision trees
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathrm{0}}$
for all decision trees
![]() ${\mathit{t}}$
as shown above. For the induction step we assume that for all decision trees
${\mathit{t}}$
as shown above. For the induction step we assume that for all decision trees
![]() ${\mathit{t}}$
of
${\mathit{t}}$
of
![]() ${\mathit{par}_{\!\mathit{n}}}$
or
${\mathit{par}_{\!\mathit{n}}}$
or
![]() ${\neg \;\mathit{par}_{\!\mathit{n}}}$
we have that
${\neg \;\mathit{par}_{\!\mathit{n}}}$
we have that
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
and show that for all decision trees
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
and show that for all decision trees
![]() ${\mathit{t}}$
of
${\mathit{t}}$
of
![]() ${\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
or
${\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
or
![]() ${\neg \;\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
we have that
${\neg \;\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
we have that
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}\mathbin{+}\mathrm{1}}$
. Any decision tree for
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}\mathbin{+}\mathrm{1}}$
. Any decision tree for
![]() ${\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
or
${\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
or
![]() ${\neg \;\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
is of the form
${\neg \;\mathit{par}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}$
is of the form
![]() ${\mathit{Pick}\;\mathit{i}\;\mathit{t}_{0}\;\mathit{t}_{1}}$
where
${\mathit{Pick}\;\mathit{i}\;\mathit{t}_{0}\;\mathit{t}_{1}}$
where
![]() ${\mathit{t}_{0}}$
and
${\mathit{t}_{0}}$
and
![]() ${\mathit{t}_{1}}$
are decision trees for
${\mathit{t}_{1}}$
are decision trees for
![]() ${\mathit{par}_{\!\mathit{n}}}$
or
${\mathit{par}_{\!\mathit{n}}}$
or
![]() ${\neg \;\mathit{par}_{\!\mathit{n}}}$
as seen in Figure 7.
${\neg \;\mathit{par}_{\!\mathit{n}}}$
as seen in Figure 7.

Fig. 7. The recursive structure of the parity function (
![]() ${\mathit{par}_{\!\mathit{n}}}$
). The pattern repeats all the way down to
${\mathit{par}_{\!\mathit{n}}}$
). The pattern repeats all the way down to
![]() ${\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{0}}{}}$
.
${\mathit{par}_{\!\mathrm{0}}\mathrel{=}{\mathit{const}_{\mathrm{0}}}\;{\mathbf{0}}{}}$
.
To calculate the expected cost, we get
Thus, the induction proof is complete and as
![]() ${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
for all decision trees then also the minimum is n, thus
${\mathit{expCost}\;\mathit{t}\mathrel{=}\mathit{n}}$
for all decision trees then also the minimum is n, thus
![]() $D_p({\mathit{par}_{\!\mathit{n}}}) = n$
. Comparing Figure 5 with Figure 7, we see that the minimum depth of the dictator tree is 1, while the minimum depth of the parity tree is n. The parity function and the constant function are interesting extreme cases of Boolean functions as they have highest and lowest possible level-
$D_p({\mathit{par}_{\!\mathit{n}}}) = n$
. Comparing Figure 5 with Figure 7, we see that the minimum depth of the dictator tree is 1, while the minimum depth of the parity tree is n. The parity function and the constant function are interesting extreme cases of Boolean functions as they have highest and lowest possible level-
![]() ${\mathit{p}}$
-complexity
${\mathit{p}}$
-complexity
![]() ${\mathit{n}}$
and 0. Either all bits have to be picked to determine the parity or none of them need to be picked to determine the constant function.
${\mathit{n}}$
and 0. Either all bits have to be picked to determine the parity or none of them need to be picked to determine the constant function.
We now introduce the Boolean function
![]() ${\mathit{same}}$
which checks if all bits are equal:
${\mathit{same}}$
which checks if all bits are equal:
Using
![]() ${\mathit{same}}$
we construct the example
${\mathit{same}}$
we construct the example
![]() ${\mathit{sim}_{5}}$
from the introduction. We first split the bits into two groups, one with the first three bits and the second with the last two bits. On the first group, called
${\mathit{sim}_{5}}$
from the introduction. We first split the bits into two groups, one with the first three bits and the second with the last two bits. On the first group, called
![]() ${\mathit{as}}$
, we check if the bits are not the same, and on the second group, called
${\mathit{as}}$
, we check if the bits are not the same, and on the second group, called
![]() ${\mathit{cs}}$
we check if the bits are the same.
${\mathit{cs}}$
we check if the bits are the same.

The point of this function is to illustrate a special case where the best decision tree depends on
![]() ${\mathit{p}}$
so that the level-
${\mathit{p}}$
so that the level-
![]() ${\mathit{p}}$
-complexity consists of more than one polynomial piece. This computation is shown in Section 4.1.
${\mathit{p}}$
-complexity consists of more than one polynomial piece. This computation is shown in Section 4.1.
One of the major goals of this paper was to calculate the level-
![]() ${\mathit{p}}$
-complexity of 9 bit iterated majority called
${\mathit{p}}$
-complexity of 9 bit iterated majority called
![]() ${\mathit{maj}_{3}^2}$
. When extending the majority function to
${\mathit{maj}_{3}^2}$
. When extending the majority function to
![]() ${\mathit{maj}_{3}^2}$
, we use
${\mathit{maj}_{3}^2}$
, we use
![]() ${\mathit{maj}_{3}}$
inside
${\mathit{maj}_{3}}$
inside
![]() ${\mathit{maj}_{3}}$
.
${\mathit{maj}_{3}}$
.

It is hard to calculate
![]() $D_p({\mathit{maj}_{3}^2})$
by hand because there are very many different decision trees, and this motivated our Haskell implementation.
$D_p({\mathit{maj}_{3}^2})$
by hand because there are very many different decision trees, and this motivated our Haskell implementation.
3 Computing the level-p-complexity
In this section, we explain how to compute the level-
![]() ${\mathit{p}}$
-complexity of a Boolean function
${\mathit{p}}$
-complexity of a Boolean function
![]() ${\mathit{f}}$
by recursively “generating all candidates” followed by “picking the best one(s)”. The naive approach would be to generate all decision trees of
${\mathit{f}}$
by recursively “generating all candidates” followed by “picking the best one(s)”. The naive approach would be to generate all decision trees of
![]() ${\mathit{f}}$
and then minimizing, but already for the 9-bit function
${\mathit{f}}$
and then minimizing, but already for the 9-bit function
![]() ${\mathit{maj}_{3}^2}$
that is intractable. To reduce the number of polynomials, we use the algorithm design technique thinning. We compare polynomials by using Yun’s algorithm and Descartes rule of signs. Further, since the same subfunctions often appear in many different nodes, we can save a significant amount of computation time using memoization.
${\mathit{maj}_{3}^2}$
that is intractable. To reduce the number of polynomials, we use the algorithm design technique thinning. We compare polynomials by using Yun’s algorithm and Descartes rule of signs. Further, since the same subfunctions often appear in many different nodes, we can save a significant amount of computation time using memoization.
The top level complexity computation (from Section 2.4) can be simplified a bit:

and we start by explaining
![]() ${{\mathit{genAlg}_{\mathit{n}}}}$
. The decision trees of a function
${{\mathit{genAlg}_{\mathit{n}}}}$
. The decision trees of a function
![]() ${\mathit{f}}$
can be described in terms of the decision trees for the immediate subfunctions (
${\mathit{f}}$
can be described in terms of the decision trees for the immediate subfunctions (
![]() $f^{i}_{b} = {\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f}}$
) for different
$f^{i}_{b} = {\mathit{setBit}\;\mathit{i}\;\mathit{b}\;\mathit{f}}$
) for different
![]() ${\mathit{i}\mathop{:}\mathit{Index}}$
and
${\mathit{i}\mathop{:}\mathit{Index}}$
and
![]() ${\mathit{b}\mathop{:}\mathbb{B}}$
. In fact, we can immediately generate elements of any tree algebra, not only decision trees, by using
${\mathit{b}\mathop{:}\mathbb{B}}$
. In fact, we can immediately generate elements of any tree algebra, not only decision trees, by using
![]() ${\mathit{res}}$
and
${\mathit{res}}$
and
![]() ${\mathit{pic}}$
instead of
${\mathit{pic}}$
instead of
![]() ${\mathit{Res}}$
and
${\mathit{Res}}$
and
![]() ${\mathit{Pick}}$
. (That is used in the “fuse” step of the calculation above.) When we explain the algorithm we write “decision tree” to make it feel more concrete, but we will in the end mostly use it to directly compute expected cost polynomials.
${\mathit{Pick}}$
. (That is used in the “fuse” step of the calculation above.) When we explain the algorithm we write “decision tree” to make it feel more concrete, but we will in the end mostly use it to directly compute expected cost polynomials.
3.1 Generating decision trees and other tree algebras
The complexity computation starts from a Boolean function
![]() ${\mathit{f}\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
and generates all decision trees for it. There are two top level cases: either the function
${\mathit{f}\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
and generates all decision trees for it. There are two top level cases: either the function
![]() ${\mathit{f}}$
is constant (and returns
${\mathit{f}}$
is constant (and returns
![]() ${\mathit{b}\mathop{:}\mathbb{B}}$
), in which case there is only one decision tree:
${\mathit{b}\mathop{:}\mathbb{B}}$
), in which case there is only one decision tree:
![]() ${\mathit{res}\;\mathit{b}}$
; or the function
${\mathit{res}\;\mathit{b}}$
; or the function
![]() ${\mathit{f}}$
still depends on some of the input bits (and thus the arity is at least 1). In the latter case, for each index
${\mathit{f}}$
still depends on some of the input bits (and thus the arity is at least 1). In the latter case, for each index
![]() ${\mathit{i}\mathop{:}\mathit{Index}}$
, we can generate two subfunctions
${\mathit{i}\mathop{:}\mathit{Index}}$
, we can generate two subfunctions
![]() $f^{i}_{{\mathbf{0}}} = {\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{f}}$
and
$f^{i}_{{\mathbf{0}}} = {\mathit{setBit}\;\mathit{i}\;{\mathbf{0}}{}\;\mathit{f}}$
and
![]() $f^{i}_{{\mathbf{1}}} = {\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{f}}$
. We then recursively generate a decision tree
$f^{i}_{{\mathbf{1}}} = {\mathit{setBit}\;\mathit{i}\;{\mathbf{1}}{}\;\mathit{f}}$
. We then recursively generate a decision tree
![]() ${\mathit{t}_{0}}$
for
${\mathit{t}_{0}}$
for
![]() $f^{i}_{{\mathbf{0}}}$
and
$f^{i}_{{\mathbf{0}}}$
and
![]() ${\mathit{t}_{1}}$
for
${\mathit{t}_{1}}$
for
![]() $f^{i}_{{\mathbf{1}}}$
and combine them to a bigger decision tree using
$f^{i}_{{\mathbf{1}}}$
and combine them to a bigger decision tree using
![]() ${\mathit{pic}\;\mathit{i}\;\mathit{t}_{0}\;\mathit{t}_{1}}$
. This is done for all combinations of
${\mathit{pic}\;\mathit{i}\;\mathit{t}_{0}\;\mathit{t}_{1}}$
. This is done for all combinations of
![]() ${\mathit{i}}$
,
${\mathit{i}}$
,
![]() ${\mathit{t}_{0}}$
, and
${\mathit{t}_{0}}$
, and
![]() ${\mathit{t}_{1}}$
in a set comprehension. To make it easier to later extend the definition (for thinning and memoization), we make the recursive step explicit.
${\mathit{t}_{1}}$
in a set comprehension. To make it easier to later extend the definition (for thinning and memoization), we make the recursive step explicit.

We would like to enumerate the cost polynomials of all the decision trees of a particular Boolean function (
![]() ${\mathit{n}\mathrel{=}\mathrm{9}}$
,
${\mathit{n}\mathrel{=}\mathrm{9}}$
,
![]() ${\mathit{f}\mathrel{=}\mathit{maj}_{3}^2}$
is our main goal). Without taking symmetries into account, there are
${\mathit{f}\mathrel{=}\mathit{maj}_{3}^2}$
is our main goal). Without taking symmetries into account, there are
![]() ${\mathrm{2}\times\mathit{n}}$
immediate subfunctions
${\mathrm{2}\times\mathit{n}}$
immediate subfunctions
![]() $f^{i}_{b}$
and if
$f^{i}_{b}$
and if
![]() $T_g$
is the cardinality of the enumeration for subfunction g we have that
$T_g$
is the cardinality of the enumeration for subfunction g we have that
 $T_{{\mathit{f}}} = \sum_{i=0}^{n-1} T_{f^{i}_{{\mathbf{0}}}}\times T_{f^{i}_{{\mathbf{1}}}}$
$T_{{\mathit{f}}} = \sum_{i=0}^{n-1} T_{f^{i}_{{\mathbf{0}}}}\times T_{f^{i}_{{\mathbf{1}}}}$
These numbers can be really big if we count all decision trees, but if we only care about their cost polynomials, many decision trees will collapse to the same polynomial, making the counts more manageable (but still possibly really big). Even the total number of subfunctions encountered (the number of recursive calls) can be quite big. If all the
![]() ${\mathrm{2}\times\mathit{n}}$
immediate subfunctions are different, and if all of them would generate
${\mathrm{2}\times\mathit{n}}$
immediate subfunctions are different, and if all of them would generate
![]() ${\mathrm{2}\times(\mathit{n}\mathbin{-}\mathrm{1})}$
different subfunctions in turn, the number of subfunctions would be
${\mathrm{2}\times(\mathit{n}\mathbin{-}\mathrm{1})}$
different subfunctions in turn, the number of subfunctions would be
![]() $2^n \times n!$
. But in practice many subfunctions will be the same. When computing the polynomials for the 9-bit function
$2^n \times n!$
. But in practice many subfunctions will be the same. When computing the polynomials for the 9-bit function
![]() ${\mathit{maj}_{3}^2}$
, for example, only
${\mathit{maj}_{3}^2}$
, for example, only
![]() ${\mathrm{215}}$
distinct subfunctions are encountered.
${\mathrm{215}}$
distinct subfunctions are encountered.
As a smaller example, for the 3-bit majority function
![]() ${\mathit{maj}_{3}}$
, choosing
${\mathit{maj}_{3}}$
, choosing
![]() ${\mathit{i}\mathrel{=}\mathrm{0},\mathrm{1},} or {\mathrm{2}}$
gives exactly the same subfunctions. Figure 8 illustrates a simplified call graph of
${\mathit{i}\mathrel{=}\mathrm{0},\mathrm{1},} or {\mathrm{2}}$
gives exactly the same subfunctions. Figure 8 illustrates a simplified call graph of
![]() ${{\mathit{genAlg}_{\mathrm{3}}}\;\mathit{maj}_{3}}$
and the results (the expected cost polynomials) for the different subfunctions. In this case, all the sets are singletons, but that is very unusual for more realistic Boolean functions. It would take too long to compute all polynomials for the 9-bit function
${{\mathit{genAlg}_{\mathrm{3}}}\;\mathit{maj}_{3}}$
and the results (the expected cost polynomials) for the different subfunctions. In this case, all the sets are singletons, but that is very unusual for more realistic Boolean functions. It would take too long to compute all polynomials for the 9-bit function
![]() ${\mathit{maj}_{3}^2}$
, but there are 21 distinct 7-bit subfunctions, and the first one of them already has
${\mathit{maj}_{3}^2}$
, but there are 21 distinct 7-bit subfunctions, and the first one of them already has
![]() ${\mathrm{18021}}$
polynomials. Thus, we can expect billions of polynomials for
${\mathrm{18021}}$
polynomials. Thus, we can expect billions of polynomials for
![]() ${\mathit{maj}_{3}^2}$
, and this means we need to look at ways to keep only the most promising candidates at each level. This leads us to the algorithmic design technique of thinning.
${\mathit{maj}_{3}^2}$
, and this means we need to look at ways to keep only the most promising candidates at each level. This leads us to the algorithmic design technique of thinning.

Fig. 8. A simplified computation tree of
![]() ${genAlg}_{\mathrm{3}}\;{maj}_{3}$
. In each node,
${genAlg}_{\mathrm{3}}\;{maj}_{3}$
. In each node,
![]() ${f}\mapsto {ps}$
shows the input f and output
${f}\mapsto {ps}$
shows the input f and output
![]() ${ps}={genAlg}_{n}\;{f}$
of each local call. As all the functions involved are “symmetric” in the index (
${ps}={genAlg}_{n}\;{f}$
of each local call. As all the functions involved are “symmetric” in the index (
![]() ${setBit}\;{i}\;{b}\;{f} == {setBit}\;{j}\;{b}\;{f}$
for all i and j), we only show edges for 0 and 1 from each level.
${setBit}\;{i}\;{b}\;{f} == {setBit}\;{j}\;{b}\;{f}$
for all i and j), we only show edges for 0 and 1 from each level.
3.2 Thinning
The general shape of the specification has two phases: “generate all candidates” followed by “pick the best one(s).” The first phase is recursive, and we would like to push as much as possible of “pick the best” into the recursive computation. In the extreme case of a greedy algorithm, we can thin the intermediate sets all the way down to singletons, but even if the sets are a bit bigger than that we can still reduce the computation cost significantly. A good (but abstract) reference for thinning is the Algebra of Programming book (Bird & de Moor, Reference Bird and de Moor1997, Chapter 8) and more concrete references are the corresponding developments in Agda (Mu et al., Reference Mu, Ko and Jansson2009) and Haskell (Bird & Gibbons, Reference Bird and Gibbons2020). In this subsection, the main focus is on specification and correctness, with Agda-like syntax for the logic part.
The “pick the best” phase is
![]() ${\mathit{best}\;\mathit{p}\mathrel{=}\mathit{minimum}\mathbin{\circ}\mathit{map}\;(\lambda \mathit{q}\,\to\,\mathit{evalP}\;\mathit{q}\;\mathit{p})} of type {\mathit{Set}\;(\mathit{Poly}\;\mathit{r})\,\to\,\mathit{r}}$
for some ring of scalars
${\mathit{best}\;\mathit{p}\mathrel{=}\mathit{minimum}\mathbin{\circ}\mathit{map}\;(\lambda \mathit{q}\,\to\,\mathit{evalP}\;\mathit{q}\;\mathit{p})} of type {\mathit{Set}\;(\mathit{Poly}\;\mathit{r})\,\to\,\mathit{r}}$
for some ring of scalars
![]() ${\mathit{r}}$
(usually rational numbers). In this context, it is clear that in the generation phase, we can throw away any polynomial which is “uniformly worse” than some other polynomial and this is what we want to use thinning for. We are looking for some “smallest” polynomials, but we only have a preorder, not a total order, which means that we may need to keep a set of incomparable candidates (elements
${\mathit{r}}$
(usually rational numbers). In this context, it is clear that in the generation phase, we can throw away any polynomial which is “uniformly worse” than some other polynomial and this is what we want to use thinning for. We are looking for some “smallest” polynomials, but we only have a preorder, not a total order, which means that we may need to keep a set of incomparable candidates (elements
![]() ${\mathit{x}\not = \mathit{y}}$
for which neither
${\mathit{x}\not = \mathit{y}}$
for which neither
![]() ${\mathit{x}\prec\mathit{y}}$
nor
${\mathit{x}\prec\mathit{y}}$
nor
![]() ${\mathit{y}\prec\mathit{x}}$
). We first describe the general setting and move to the specifics of our polynomials later.
${\mathit{y}\prec\mathit{x}}$
). We first describe the general setting and move to the specifics of our polynomials later.
We start from a strict preorder
![]() ${(\prec)\mathop{:}\mathit{a}\,\to\,\mathit{a}\,\to\,\mathit{Prop}}$
(an irreflexive and transitive relation). You can think of
${(\prec)\mathop{:}\mathit{a}\,\to\,\mathit{a}\,\to\,\mathit{Prop}}$
(an irreflexive and transitive relation). You can think of
![]() ${\mathit{Prop}}$
as
${\mathit{Prop}}$
as
![]() ${\mathbb{B}}$
because we only work with decidable relations and finite sets in this application. As we are looking for minima, we say that
${\mathbb{B}}$
because we only work with decidable relations and finite sets in this application. As we are looking for minima, we say that
![]() ${\mathit{y}}$
dominates
${\mathit{y}}$
dominates
![]() ${\mathit{x}}$
if
${\mathit{x}}$
if
![]() ${\mathit{y}\prec\mathit{x}}$
.
${\mathit{y}\prec\mathit{x}}$
.
We lift the order relation to sets in two steps. First,
![]() ${\mathit{ys}\mathrel{\dot{\prec}}\mathit{x}}$
means that
${\mathit{ys}\mathrel{\dot{\prec}}\mathit{x}}$
means that
![]() ${\mathit{ys}}$
dominates
${\mathit{ys}}$
dominates
![]() ${\mathit{x}}$
, meaning that some element in
${\mathit{x}}$
, meaning that some element in
![]() ${\mathit{ys}}$
is smaller than
${\mathit{ys}}$
is smaller than
![]() ${\mathit{x}}$
. If this holds, there is no need to add
${\mathit{x}}$
. If this holds, there is no need to add
![]() ${\mathit{x}}$
to
${\mathit{x}}$
to
![]() ${\mathit{ys}}$
because we already have at least one better element in
${\mathit{ys}}$
because we already have at least one better element in
![]() ${\mathit{ys}}$
. Then
${\mathit{ys}}$
. Then
![]() ${\mathit{ys}\mathrel{\ddot{\prec}}\mathit{xs}}$
means that
${\mathit{ys}\mathrel{\ddot{\prec}}\mathit{xs}}$
means that
![]() ${\mathit{ys}}$
dominates all of
${\mathit{ys}}$
dominates all of
![]() ${\mathit{xs}}$
.
${\mathit{xs}}$
.

Finally, we combine subset and domination into the thinning relation:
We will use this relation in the specification of our efficient computation to ensure that the small set of polynomials computed, still “dominates” the big set of all the polynomials generated by
![]() ${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
.
${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
.
But first we introduce the helper function
![]() ${\mathit{thin}\mathop{:}\mathit{Set}\;\mathit{a}\,\to\,\mathit{Set}\;\mathit{a}}$
which aims at removing some elements, while still keeping the minima in the set. Later, we will use the function
${\mathit{thin}\mathop{:}\mathit{Set}\;\mathit{a}\,\to\,\mathit{Set}\;\mathit{a}}$
which aims at removing some elements, while still keeping the minima in the set. Later, we will use the function
![]() ${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
specified similarly to
${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
specified similarly to
![]() ${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
but using the helper function
${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
but using the helper function
![]() ${\mathit{thin}}$
. It has to refine the relation
${\mathit{thin}}$
. It has to refine the relation
![]() ${\mathit{Thin}}$
which means that if
${\mathit{Thin}}$
which means that if
![]() ${\mathit{ys}\mathrel{=}\mathit{thin}\;\mathit{xs}}$
then
${\mathit{ys}\mathrel{=}\mathit{thin}\;\mathit{xs}}$
then
![]() ${\mathit{ys}}$
must be a subset of
${\mathit{ys}}$
must be a subset of
![]() ${\mathit{xs}}$
(
${\mathit{xs}}$
(
![]() ${\mathit{ys}\subseteq\mathit{xs}}$
) and
${\mathit{ys}\subseteq\mathit{xs}}$
) and
![]() ${\mathit{ys}}$
must dominate the rest of
${\mathit{ys}}$
must dominate the rest of
![]() ${\mathit{xs}}$
(
${\mathit{xs}}$
(
![]() ${\mathit{ys}\mathrel{\ddot{\prec}}(\mathit{xs} \backslash \backslash \mathit{ys})}$
). A trivial (but useless) implementation would be
${\mathit{ys}\mathrel{\ddot{\prec}}(\mathit{xs} \backslash \backslash \mathit{ys})}$
). A trivial (but useless) implementation would be
![]() ${\mathit{thin}\mathrel{=}\mathit{id}}$
, and any implementation which removes some “dominated” elements could be helpful. The best we can hope for is that
${\mathit{thin}\mathrel{=}\mathit{id}}$
, and any implementation which removes some “dominated” elements could be helpful. The best we can hope for is that
![]() ${\mathit{thin}}$
gives us a set of only incomparable elements. If
${\mathit{thin}}$
gives us a set of only incomparable elements. If
![]() ${\mathit{thin}}$
compares all pairs of elements, it can compute a smallest thinning. In general that may not be needed (and a linear time greedy approximation is good enough), but in some settings almost any algorithmic cost which can reduce the intermediate sets will pay off. We collect the thinning functions in the type class
${\mathit{thin}}$
compares all pairs of elements, it can compute a smallest thinning. In general that may not be needed (and a linear time greedy approximation is good enough), but in some settings almost any algorithmic cost which can reduce the intermediate sets will pay off. We collect the thinning functions in the type class
![]() ${\mathit{Thinnable}}$
:
${\mathit{Thinnable}}$
:

The greedy
![]() ${\mathit{thin}}$
starts from an empty set and considers one element
${\mathit{thin}}$
starts from an empty set and considers one element
![]() ${\mathit{x}}$
at a time. If the set
${\mathit{x}}$
at a time. If the set
![]() ${\mathit{ys}}$
collected thus far already dominates
${\mathit{ys}}$
collected thus far already dominates
![]() ${\mathit{x}}$
, it is returned unchanged, otherwise
${\mathit{x}}$
, it is returned unchanged, otherwise
![]() ${\mathit{x}}$
is inserted. The optimal version also removes from
${\mathit{x}}$
is inserted. The optimal version also removes from
![]() ${\mathit{ys}}$
all elements dominated by
${\mathit{ys}}$
all elements dominated by
![]() ${\mathit{x}}$
. It is easy to prove that
${\mathit{x}}$
. It is easy to prove that
![]() ${\mathit{thin}}$
implements the specification
${\mathit{thin}}$
implements the specification
![]() ${\mathit{Thin}}$
.
${\mathit{Thin}}$
.
The method
![]() ${\mathit{cmp}}$
is a more informative version of
${\mathit{cmp}}$
is a more informative version of
![]() ${(\prec)}: it returns {\mathit{Just}\;\mathit{LT}}$
,
${(\prec)}: it returns {\mathit{Just}\;\mathit{LT}}$
,
![]() ${\mathit{Just}\;\mathit{EQ}}$
, or
${\mathit{Just}\;\mathit{EQ}}$
, or
![]() ${\mathit{Just}\;\mathit{GT}}$
if the first element is smaller, equal, or greater than the second, respectively, or
${\mathit{Just}\;\mathit{GT}}$
if the first element is smaller, equal, or greater than the second, respectively, or
![]() ${\mathit{Nothing}}$
if they are incomparable.
${\mathit{Nothing}}$
if they are incomparable.
Our use of thinning. Now we have what we need to specify when an efficient
![]() ${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
computation is correct. Our specification (
${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
computation is correct. Our specification (
![]() ${\mathit{spec}\;\mathit{n}\;\mathit{f}}$
) states a relation between a (very big) set
${\mathit{spec}\;\mathit{n}\;\mathit{f}}$
) states a relation between a (very big) set
![]() ${\mathit{xs}\mathrel{=}{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and a smaller set
${\mathit{xs}\mathrel{=}{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and a smaller set
![]() ${\mathit{ys}\mathrel{=}{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
, we get by applying thinning at each recursive step. We want to prove that
${\mathit{ys}\mathrel{=}{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
, we get by applying thinning at each recursive step. We want to prove that
![]() ${\mathit{ys}\subseteq\mathit{xs}}$
and
${\mathit{ys}\subseteq\mathit{xs}}$
and
![]() ${\mathit{ys}\mathrel{\ddot{\prec}}(\mathit{xs} \backslash \backslash \mathit{ys})}$
because then we know we have kept all the candidates for minimality.
${\mathit{ys}\mathrel{\ddot{\prec}}(\mathit{xs} \backslash \backslash \mathit{ys})}$
because then we know we have kept all the candidates for minimality.

We can first take care of the simplest case (for any
![]() ${\mathit{n}}$
). If the function
${\mathit{n}}$
). If the function
![]() ${\mathit{f}}$
is constant (returning some
${\mathit{f}}$
is constant (returning some
![]() ${\mathit{b}\mathop{:}\mathbb{B}}$
), both
${\mathit{b}\mathop{:}\mathbb{B}}$
), both
![]() ${\mathit{xs}}$
and
${\mathit{xs}}$
and
![]() ${\mathit{ys}}$
will be the singleton set containing
${\mathit{ys}}$
will be the singleton set containing
![]() ${\mathit{res}\;\mathit{b}}$
. Thus, both properties trivially hold.
${\mathit{res}\;\mathit{b}}$
. Thus, both properties trivially hold.
We then proceed by induction on
![]() ${\mathit{n}}$
to prove
${\mathit{n}}$
to prove
![]() ${\mathit{S}_{\mathit{n}}\mathrel{=}\forall\,\mathit{f}\mathop{:}\mathit{BoolFun}\;\mathit{n}.\,\,\mathit{spec}\;\mathit{n}\;\mathit{f}}$
. In the base case
${\mathit{S}_{\mathit{n}}\mathrel{=}\forall\,\mathit{f}\mathop{:}\mathit{BoolFun}\;\mathit{n}.\,\,\mathit{spec}\;\mathit{n}\;\mathit{f}}$
. In the base case
![]() ${\mathit{n}\mathrel{=}\mathrm{0}}$
the function is necessarily constant, and we have already covered that above. In the inductive step case, assume the induction hypothesis
${\mathit{n}\mathrel{=}\mathrm{0}}$
the function is necessarily constant, and we have already covered that above. In the inductive step case, assume the induction hypothesis
![]() ${\mathit{IH}\mathrel{=}\mathit{S}_{\mathit{n}}}$
and prove
${\mathit{IH}\mathrel{=}\mathit{S}_{\mathit{n}}}$
and prove
![]() ${\mathit{S}_{\mathit{n}\mathbin{+}\mathrm{1}}}$
for a function
${\mathit{S}_{\mathit{n}\mathbin{+}\mathrm{1}}}$
for a function
![]() ${\mathit{f}\mathop{:}\mathit{BoolFun}\;(\mathit{n}\mathbin{+}\mathrm{1})}$
. We have already covered the constant function case, so we focus on the main recursive clause of the definitions of
${\mathit{f}\mathop{:}\mathit{BoolFun}\;(\mathit{n}\mathbin{+}\mathrm{1})}$
. We have already covered the constant function case, so we focus on the main recursive clause of the definitions of
![]() ${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and
${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and
![]() ${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
when the fixpoint definitions have been expanded:
${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
when the fixpoint definitions have been expanded:
All subfunctions
![]() ${\mathit{f}^{\mathit{i}}_{\mathit{b}}\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
used in the recursive calls satisfy the induction hypothesis:
${\mathit{f}^{\mathit{i}}_{\mathit{b}}\mathop{:}\mathit{BoolFun}\;\mathit{n}}$
used in the recursive calls satisfy the induction hypothesis:
![]() ${\mathit{spec}\;\mathit{n}\;\mathit{f}^{\mathit{i}}_{\mathit{b}}}$
. If we name the sets involved in these hypotheses
${\mathit{spec}\;\mathit{n}\;\mathit{f}^{\mathit{i}}_{\mathit{b}}}$
. If we name the sets involved in these hypotheses
![]() ${\mathit{xs}^{\mathit{i}}_{\mathit{b}}}$
and
${\mathit{xs}^{\mathit{i}}_{\mathit{b}}}$
and
![]() ${\mathit{ys}^{\mathit{i}}_{\mathit{b}}}$
, we can thus assume
${\mathit{ys}^{\mathit{i}}_{\mathit{b}}}$
, we can thus assume
![]() ${\mathit{ys}^{\mathit{i}}_{\mathit{b}}\subseteq\mathit{xs}^{\mathit{i}}_{\mathit{b}}}$
and
${\mathit{ys}^{\mathit{i}}_{\mathit{b}}\subseteq\mathit{xs}^{\mathit{i}}_{\mathit{b}}}$
and
![]() ${\mathit{ys}^{\mathit{i}}_{\mathit{b}}\mathrel{\ddot{\prec}}(\mathit{xs}^{\mathit{i}}_{\mathit{b}} \backslash \backslash \mathit{ys}^{\mathit{i}}_{\mathit{b}})}$
.
${\mathit{ys}^{\mathit{i}}_{\mathit{b}}\mathrel{\ddot{\prec}}(\mathit{xs}^{\mathit{i}}_{\mathit{b}} \backslash \backslash \mathit{ys}^{\mathit{i}}_{\mathit{b}})}$
.
First, the subset property: we want to prove that
![]() ${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}\subseteq{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
, or equivalently,
${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}\subseteq{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
, or equivalently,
![]() ${\forall\,\mathit{y}.\,\,(\mathit{y}\in {\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f})\Rightarrow (\mathit{y}\in {\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f})}$
. Let
${\forall\,\mathit{y}.\,\,(\mathit{y}\in {\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f})\Rightarrow (\mathit{y}\in {\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f})}$
. Let
![]() ${\mathit{y}\in {\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
. We know from the specification of
${\mathit{y}\in {\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
. We know from the specification of
![]() ${\mathit{thin}}$
and the definition of
${\mathit{thin}}$
and the definition of
![]() ${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
![]() ${\mathit{y}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{y}_{0}\;\mathit{y}_{1}}$
for some
${\mathit{y}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{y}_{0}\;\mathit{y}_{1}}$
for some
![]() ${\mathit{y}_{0}\in \mathit{ys}^{\mathit{i}}_{\mathrm{0}}}$
and
${\mathit{y}_{0}\in \mathit{ys}^{\mathit{i}}_{\mathrm{0}}}$
and
![]() ${\mathit{y}_{1}\in \mathit{ys}^{\mathit{i}}_{\mathrm{1}}}$
. The subset part of the induction hypothesis gives us that
${\mathit{y}_{1}\in \mathit{ys}^{\mathit{i}}_{\mathrm{1}}}$
. The subset part of the induction hypothesis gives us that
![]() ${\mathit{y}_{0}\in \mathit{xs}^{\mathit{i}}_{\mathrm{0}}}$
and
${\mathit{y}_{0}\in \mathit{xs}^{\mathit{i}}_{\mathrm{0}}}$
and
![]() ${\mathit{y}_{1}\in \mathit{xs}^{\mathit{i}}_{\mathrm{1}}}$
. Thus, we can see from the definition of
${\mathit{y}_{1}\in \mathit{xs}^{\mathit{i}}_{\mathrm{1}}}$
. Thus, we can see from the definition of
![]() ${{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
${{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
![]() ${\mathit{y}\in {\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
.
${\mathit{y}\in {\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
.
Now for the “domination” property we need to show that
![]() ${\forall\,\mathit{x}\in \mathit{xs} \backslash \backslash \mathit{ys}.\,\,\mathit{ys}\mathrel{\dot{\prec}}\mathit{x}}$
where
${\forall\,\mathit{x}\in \mathit{xs} \backslash \backslash \mathit{ys}.\,\,\mathit{ys}\mathrel{\dot{\prec}}\mathit{x}}$
where
![]() ${\mathit{xs}\mathrel{=}{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
and
${\mathit{xs}\mathrel{=}{\mathit{genAlg}_{\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
and
![]() ${\mathit{ys}\mathrel{=}{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
. Let
${\mathit{ys}\mathrel{=}{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
. Let
![]() ${\mathit{x}\in \mathit{xs} \backslash \backslash \mathit{ys}}$
. Given the definition of
${\mathit{x}\in \mathit{xs} \backslash \backslash \mathit{ys}}$
. Given the definition of
![]() ${\mathit{xs}}$
it must be of the form
${\mathit{xs}}$
it must be of the form
![]() ${\mathit{x}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{x}_{0}\;\mathit{x}_{1}}$
where
${\mathit{x}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{x}_{0}\;\mathit{x}_{1}}$
where
![]() ${\mathit{x}_{0}\in \mathit{xs}^{\mathit{i}}_{{\mathbf{0}}{}}}$
and
${\mathit{x}_{0}\in \mathit{xs}^{\mathit{i}}_{{\mathbf{0}}{}}}$
and
![]() ${\mathit{x}_{1}\in \mathit{xs}^{\mathit{i}}_{{\mathbf{1}}{}}}$
. The (second part of the) induction hypothesis provides the existence of
${\mathit{x}_{1}\in \mathit{xs}^{\mathit{i}}_{{\mathbf{1}}{}}}$
. The (second part of the) induction hypothesis provides the existence of
![]() ${\mathit{y}_{\mathit{b}}\in \mathit{ys}^{\mathit{i}}_{\mathit{b}}}$
such that
${\mathit{y}_{\mathit{b}}\in \mathit{ys}^{\mathit{i}}_{\mathit{b}}}$
such that
![]() ${\mathit{y}_{\mathit{b}}\prec\mathit{x}_{\mathit{b}}}$
. From these
${\mathit{y}_{\mathit{b}}\prec\mathit{x}_{\mathit{b}}}$
. From these
![]() ${\mathit{y}_{\mathit{b}}}$
we can build
${\mathit{y}_{\mathit{b}}}$
we can build
![]() ${\mathit{y'}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{y}_{0}\;\mathit{y}_{1}}$
as a candidate element to “dominate”
${\mathit{y'}\mathrel{=}\mathit{pic}\;\mathit{i}\;\mathit{y}_{0}\;\mathit{y}_{1}}$
as a candidate element to “dominate”
![]() ${\mathit{xs}}$
.
${\mathit{xs}}$
.
We can now show that
![]() ${\mathit{y'}\prec\mathit{x}}$
by polynomial algebra:
${\mathit{y'}\prec\mathit{x}}$
by polynomial algebra:

We are not quite done, because
![]() ${\mathit{y'}}$
may not be in
${\mathit{y'}}$
may not be in
![]() ${\mathit{ys}}$
. It is clear from the definition of
${\mathit{ys}}$
. It is clear from the definition of
![]() ${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
${{\mathit{genAlgT}_{\!\mathit{n}\mathbin{+}\mathrm{1}}}\;\mathit{f}}$
that
![]() ${\mathit{y'}}$
is in the set
${\mathit{y'}}$
is in the set
![]() ${\mathit{ys'}}$
sent to
${\mathit{ys'}}$
sent to
![]() ${\mathit{thin}}$
, but it may be “thinned away.” But, either
${\mathit{thin}}$
, but it may be “thinned away.” But, either
![]() ${\mathit{y'}\in \mathit{ys}\mathrel{=}\mathit{thin}\;\mathit{ys'}}$
in which case we take the final
${\mathit{y'}\in \mathit{ys}\mathrel{=}\mathit{thin}\;\mathit{ys'}}$
in which case we take the final
![]() ${\mathit{y}\mathrel{=}\mathit{y'}}$
or there exists another
${\mathit{y}\mathrel{=}\mathit{y'}}$
or there exists another
![]() ${\mathit{y}\in \mathit{ys}}$
such that
${\mathit{y}\in \mathit{ys}}$
such that
![]() ${\mathit{y}\prec\mathit{y'}}$
and then we get get
${\mathit{y}\prec\mathit{y'}}$
and then we get get
![]() ${\mathit{y}\prec\mathit{x}}$
by transitivity.
${\mathit{y}\prec\mathit{x}}$
by transitivity.
To sum up, we have now proved that we can push a powerful
![]() ${\mathit{thin}}$
step into the recursive enumeration of all cost polynomials in such a way that any minimum is guaranteed to reside in the much smaller set of polynomials thus computed.
${\mathit{thin}}$
step into the recursive enumeration of all cost polynomials in such a way that any minimum is guaranteed to reside in the much smaller set of polynomials thus computed.
The specific properties we need from
![]() ${(\prec)}$
(in addition to the general requirements for thinning) are that
${(\prec)}$
(in addition to the general requirements for thinning) are that
![]() ${(\mathit{pos}\mathbin{+})}$
and
${(\mathit{pos}\mathbin{+})}$
and
![]() ${(\mathit{pos}\times)}$
are monotonic (for polynomials
${(\mathit{pos}\times)}$
are monotonic (for polynomials
![]() ${\mathrm{0}\prec\mathit{pos}}$
) and that
${\mathrm{0}\prec\mathit{pos}}$
) and that
![]() ${\mathit{q}_{0}\prec\mathit{q}_{1}}$
implies
${\mathit{q}_{0}\prec\mathit{q}_{1}}$
implies
![]() ${\mathit{evalP}\;\mathit{q}_{0}\;\mathit{p}{\leqslant} \mathit{evalP}\;\mathit{q}_{1}\;\mathit{p}}$
for all
${\mathit{evalP}\;\mathit{q}_{0}\;\mathit{p}{\leqslant} \mathit{evalP}\;\mathit{q}_{1}\;\mathit{p}}$
for all
![]() ${\mathrm{0}{\leqslant} \mathit{p}{\leqslant} \mathrm{1}}$
.
${\mathrm{0}{\leqslant} \mathit{p}{\leqslant} \mathrm{1}}$
.
3.3 Memoization
The call graph of
![]() ${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
is the same as the call graph of
${{\mathit{genAlgT}_{\!\mathit{n}}}\;\mathit{f}}$
is the same as the call graph of
![]() ${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and, as mentioned above, it can be exponentially big. Thus, even though thinning helps in making the intermediate sets exponentially smaller, we still have one source of exponential computational complexity to tackle. Fortunately, the same subfunctions often appear in many different nodes and this means we can save a significant amount of computation time using memoization.
${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
and, as mentioned above, it can be exponentially big. Thus, even though thinning helps in making the intermediate sets exponentially smaller, we still have one source of exponential computational complexity to tackle. Fortunately, the same subfunctions often appear in many different nodes and this means we can save a significant amount of computation time using memoization.
The classical example of memoization is the Fibonacci function. Naively computing
![]() ${\mathit{fib}\;(\mathit{n}\mathbin{+}\mathrm{2})\mathrel{=}\mathit{fib}\;(\mathit{n}\mathbin{+}\mathrm{1})\mathbin{+}\mathit{fib}\;\mathit{n}}$
leads to exponential growth in the number of function calls. But if we fill in a table indexed by
${\mathit{fib}\;(\mathit{n}\mathbin{+}\mathrm{2})\mathrel{=}\mathit{fib}\;(\mathit{n}\mathbin{+}\mathrm{1})\mathbin{+}\mathit{fib}\;\mathit{n}}$
leads to exponential growth in the number of function calls. But if we fill in a table indexed by
![]() ${\mathit{n}}$
with already computed results we can compute
${\mathit{n}}$
with already computed results we can compute
![]() ${\mathit{fib}\;\mathit{n}}$
in linear time.
${\mathit{fib}\;\mathit{n}}$
in linear time.
Similarly, here we “just” need to tabulate the result of the calls to
![]() ${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
so as to avoid recomputation. The challenge is that the input we need to tabulate is now a Boolean function, which is not as nicely structured as a natural number index. Fortunately, thanks to Hinze (Reference Hinze2000), Elliott, and others we have generic Trie-based memo functions only a hackage library away
Footnote 5
. The
${{\mathit{genAlg}_{\mathit{n}}}\;\mathit{f}}$
so as to avoid recomputation. The challenge is that the input we need to tabulate is now a Boolean function, which is not as nicely structured as a natural number index. Fortunately, thanks to Hinze (Reference Hinze2000), Elliott, and others we have generic Trie-based memo functions only a hackage library away
Footnote 5
. The
![]() ${\mathit{MemoTrie}}$
library provides the
${\mathit{MemoTrie}}$
library provides the
![]() ${\mathit{Memoizable}}$
class and suitable instances and helper functions for most types. We only need to provide a
${\mathit{Memoizable}}$
class and suitable instances and helper functions for most types. We only need to provide a
![]() ${\mathit{Memoizable}}$
instance for
${\mathit{Memoizable}}$
instance for
![]() ${\mathit{BDD}}$
s, and we do this using
${\mathit{BDD}}$
s, and we do this using
![]() ${\mathit{inSig}}$
and
${\mathit{inSig}}$
and
![]() ${\mathit{outSig}}$
from the
${\mathit{outSig}}$
from the
![]() ${\mathit{BDD}}$
package (decision-diagrams). They expose the top-level structure of a
${\mathit{BDD}}$
package (decision-diagrams). They expose the top-level structure of a
![]() ${\mathit{BDD}}: {\mathit{Sig}\;\mathit{bf}}$
is isomorphic to
${\mathit{BDD}}: {\mathit{Sig}\;\mathit{bf}}$
is isomorphic to
![]() ${\mathit{Either}\;\mathbb{B}\;(\mathit{Index},\mathit{bf},\mathit{bf})}$
where
${\mathit{Either}\;\mathbb{B}\;(\mathit{Index},\mathit{bf},\mathit{bf})}$
where
![]() ${\mathit{bf}\mathrel{=}\mathit{BDDFun}}$
. We define our top-level function
${\mathit{bf}\mathrel{=}\mathit{BDDFun}}$
. We define our top-level function
![]() ${\mathit{genAlgThinMemo}}$
by applying memoization to
${\mathit{genAlgThinMemo}}$
by applying memoization to
![]() ${{\mathit{genAlgT}_{\!\mathit{n}}}}$
(or, more specifically, to
${{\mathit{genAlgT}_{\!\mathit{n}}}}$
(or, more specifically, to
![]() ${\mathit{genAlgStepThin}}$
).
${\mathit{genAlgStepThin}}$
).
3.4 Comparing polynomials
As argued in Section 3.2, the key to an efficient computation of the best cost polynomials is to compare polynomials as soon as possible and throw away those which are “uniformly worse.” The specification of
![]() ${\mathit{p}\prec\mathit{q}}$
is
${\mathit{p}\prec\mathit{q}}$
is
![]() ${\mathit{p}\;\mathit{x}{\leqslant} \mathit{q}\;\mathit{x}}$
for all
${\mathit{p}\;\mathit{x}{\leqslant} \mathit{q}\;\mathit{x}}$
for all
![]() ${\mathrm{0}{\leqslant} \mathit{x}{\leqslant} \mathrm{1}}$
and
${\mathrm{0}{\leqslant} \mathit{x}{\leqslant} \mathrm{1}}$
and
![]() ${\mathit{p}\;\mathit{x}\mathbin{<}\mathit{q}\;\mathit{x}}$
for some
${\mathit{p}\;\mathit{x}\mathbin{<}\mathit{q}\;\mathit{x}}$
for some
![]() ${\mathrm{0}\mathbin{<}\mathit{x}\mathbin{<}\mathrm{1}}$
. Note that
${\mathrm{0}\mathbin{<}\mathit{x}\mathbin{<}\mathrm{1}}$
. Note that
![]() ${(\prec)}$
is a strict preorder — if the polynomials cross, neither is “uniformly worse” and we keep both. A simple example of two incomparable polynomials is
${(\prec)}$
is a strict preorder — if the polynomials cross, neither is “uniformly worse” and we keep both. A simple example of two incomparable polynomials is
![]() ${\mathit{xP}}$
and
${\mathit{xP}}$
and
![]() ${\mathrm{1}\mathbin{-}\mathit{xP}}$
which cross at
${\mathrm{1}\mathbin{-}\mathit{xP}}$
which cross at
![]() ${\mathit{p}\mathrel{=}{1}/{2}}$
.
${\mathit{p}\mathrel{=}{1}/{2}}$
.
If we have two polynomials
![]() ${\mathit{p}}$
and
${\mathit{p}}$
and
![]() ${\mathit{q}}$
, we want to know if
${\mathit{q}}$
, we want to know if
![]() ${\mathit{p}{\leqslant} \mathit{q}}$
for all inputs in the interval
${\mathit{p}{\leqslant} \mathit{q}}$
for all inputs in the interval
![]() ${[\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu]}$
. Equivalently, we need to check if
${[\mskip1.5mu \mathrm{0},\mathrm{1}\mskip1.5mu]}$
. Equivalently, we need to check if
![]() ${\mathrm{0}{\leqslant} \mathit{q}\mathbin{-}\mathit{p}}$
in that interval.
${\mathrm{0}{\leqslant} \mathit{q}\mathbin{-}\mathit{p}}$
in that interval.
As the difference is also a polynomial, we can focus our attention to locating polynomial roots in the unit interval.
If there are no roots (Figure 9a) in the unit interval, the polynomial stays on “one side of zero,” and we just need to check the sign of the polynomial at any point. If there is at least one single root (Figure 9b), the original polynomials cross and we return
![]() ${\mathit{Nothing}}$
. Similarly for triple roots or roots of any odd order. Finally, if the polynomial only has roots of even order (some double roots, or quadruple roots, etc. as in Figure 9c) the polynomial stays on one side of zero, and we can check a few points to see what side that is. (If the number of distinct roots is
${\mathit{Nothing}}$
. Similarly for triple roots or roots of any odd order. Finally, if the polynomial only has roots of even order (some double roots, or quadruple roots, etc. as in Figure 9c) the polynomial stays on one side of zero, and we can check a few points to see what side that is. (If the number of distinct roots is
![]() ${\mathit{r}}$
we check up to
${\mathit{r}}$
we check up to
![]() ${\mathit{r}\mathbin{+}\mathrm{1}}$
points to make sure at least one will be nonzero and thus tell us on which side of zero the polynomial lies.)
${\mathit{r}\mathbin{+}\mathrm{1}}$
points to make sure at least one will be nonzero and thus tell us on which side of zero the polynomial lies.)

Fig. 9. To compare two polynomials
![]() ${\mathit{p}}$
and
${\mathit{p}}$
and
![]() ${\mathit{q}}$
we use root counting for
${\mathit{q}}$
we use root counting for
![]() ${\mathit{q}\mathbin{-}\mathit{p}}$
and these are the three main cases to consider.
${\mathit{q}\mathbin{-}\mathit{p}}$
and these are the three main cases to consider.
To compare polynomials, we thus need to implement the root-counting functions
![]() ${\mathit{numRoots}}$
and
${\mathit{numRoots}}$
and
![]() ${\mathit{numRoots'}}$
:
${\mathit{numRoots'}}$
:

We will not provide all the code here, because that would take us too far from the main topic of the paper, but we will illustrate the main algorithms and concepts for root counting in Section 3.5. The second function computes real root multiplicities:
![]() ${\mathit{numRoots'}\;\mathit{p}\mathrel{=}[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]} means {\mathit{p}}$
has one single and one triple root in the open interval
${\mathit{numRoots'}\;\mathit{p}\mathrel{=}[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]} means {\mathit{p}}$
has one single and one triple root in the open interval
![]() ${(\mathrm{0},\mathrm{1})}$
. From this we get that
${(\mathrm{0},\mathrm{1})}$
. From this we get that
![]() ${\mathit{p}}$
has
${\mathit{p}}$
has
![]() ${\mathrm{2}\mathrel{=}\mathit{length}\;[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]}$
distinct real roots and
${\mathrm{2}\mathrel{=}\mathit{length}\;[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]}$
distinct real roots and
![]() ${\mathrm{4}\mathrel{=}\mathit{sum}\;[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]}$
real roots if we count multiplicities.
${\mathrm{4}\mathrel{=}\mathit{sum}\;[\mskip1.5mu \mathrm{1},\mathrm{3}\mskip1.5mu]}$
real roots if we count multiplicities.
Using the root-counting functions, the top level of the polynomial partial order implementation is as follows:

3.5 Isolating real roots and Descartes rule of signs
This section explains how to do root counting by combining Yun’s algorithm and Descartes rule of signs. As explained in Section 3.4, the root counting is the key to implementing comparison, which is needed for thinning. First out is Yun’s algorithm (Yun, Reference Yun1976) for square-free factorization: given a polynomial
![]() ${\mathit{p}}$
it computes a list of polynomial factors
${\mathit{p}}$
it computes a list of polynomial factors
![]() $p_i$
, each of which only has single roots, and such that
$p_i$
, each of which only has single roots, and such that
![]() $p = C \prod_{i} {p_i}^i$
. Note the exponent
$p = C \prod_{i} {p_i}^i$
. Note the exponent
![]() ${\mathit{i}}$
: the factor
${\mathit{i}}$
: the factor
![]() ${\mathit{p}_{2}}$
, for example, appears squared in
${\mathit{p}_{2}}$
, for example, appears squared in
![]() ${\mathit{p}}$
. If
${\mathit{p}}$
. If
![]() ${\mathit{p}}$
only has single roots, the list from Yun’s algorithm has just one element,
${\mathit{p}}$
only has single roots, the list from Yun’s algorithm has just one element,
![]() ${\mathit{p}_{1}}$
, but in any case we get a finite list of polynomials, each of which is “square-free.”Footnote 6
${\mathit{p}_{1}}$
, but in any case we get a finite list of polynomials, each of which is “square-free.”Footnote 6
Second in line is Descartes rule of signs that can be used to determine the number of real zeros of a polynomial function. It tells us that the number of positive real zeros in a polynomial function
![]() ${\mathit{f}}$
is the same, or less than by an even number, as the number of changes in the sign of the coefficients. Together with some polynomial transformations, this is used to count the zeros in the interval [0,1).
${\mathit{f}}$
is the same, or less than by an even number, as the number of changes in the sign of the coefficients. Together with some polynomial transformations, this is used to count the zeros in the interval [0,1).
If the rule gives zero or one, we are done: we have isolated an interval [0,1) with either no root or exactly one root. For our use case, we do not need to know the actual root, just if it exists in the interval or not.
If the rule gives more than one, we do not quite know the exact number of roots yet (only an upper bound). In that case, we subdivide the interval into the lower
![]() $[0,1/2)$
and upper
$[0,1/2)$
and upper
![]() $[1/2, 1)$
halves. Fortunately, the polynomial coefficients can be transformed to make the domain the unit interval again so that we can call ourselves recursively. After a finite number of steps, this bisection terminates, and we get a list of disjoint isolating intervals where we know there is exactly one root in each. (The number of steps is on the order of the two-logarithm of the minimum distance between two distinct roots.)
$[1/2, 1)$
halves. Fortunately, the polynomial coefficients can be transformed to make the domain the unit interval again so that we can call ourselves recursively. After a finite number of steps, this bisection terminates, and we get a list of disjoint isolating intervals where we know there is exactly one root in each. (The number of steps is on the order of the two-logarithm of the minimum distance between two distinct roots.)
Combining Yun and Descartes, we implement our “root counter,” and thus our partial order on polynomials.
4 Results
Using the method from the previous section, we can now calculate the level-p-complexity of Boolean functions with our function
![]() ${\mathit{genAlgThinMemo}}$
. First, we return to our example from the beginning (
${\mathit{genAlgThinMemo}}$
. First, we return to our example from the beginning (
![]() ${\mathit{sim}_{5}}$
), where we get several polynomials which are optimal in different intervals. Then, we calculate the level-p-complexity for
${\mathit{sim}_{5}}$
), where we get several polynomials which are optimal in different intervals. Then, we calculate the level-p-complexity for
![]() ${\mathit{maj}_{3}^2}$
which is lower than the proposed result in Jansson (Reference Jansson2022), which means that our current method is better.
${\mathit{maj}_{3}^2}$
which is lower than the proposed result in Jansson (Reference Jansson2022), which means that our current method is better.
4.1 Level-p-complexity for
 ${\mathit{sim}_{5}}$
${\mathit{sim}_{5}}$
When we run
![]() ${\mathit{genAlgThinMemo}\;\mathrm{5}\;\mathit{sim}_{5}}$
it returns a set of four polynomials:
${\mathit{genAlgThinMemo}\;\mathrm{5}\;\mathit{sim}_{5}}$
it returns a set of four polynomials:
We do not compute their intersection points, but we know that they do intersect in the unit interval. The four polynomials were shown already in Figure 1. The level-p-complexity for
![]() ${\mathit{sim}_{5}}$
is the piecewise polynomial, pointwise minimum, of these four, with two different polynomials in different intervals:
${\mathit{sim}_{5}}$
is the piecewise polynomial, pointwise minimum, of these four, with two different polynomials in different intervals:
![]() $D_p({\mathit{sim}_{5}}) = P_4(p)$
for
$D_p({\mathit{sim}_{5}}) = P_4(p)$
for
![]() $p \in [\approx0.356,\approx0.644]$
and
$p \in [\approx0.356,\approx0.644]$
and
![]() $D_p({\mathit{sim}_{5}}) = P_1(p)$
in the rest of the unit interval. As seen in Figure 10, the level-p-complexity has two maxima.
$D_p({\mathit{sim}_{5}}) = P_1(p)$
in the rest of the unit interval. As seen in Figure 10, the level-p-complexity has two maxima.

Fig. 10. Fig. 10. Level-
![]() ${\mathit{p}}$
-complexity of
${\mathit{p}}$
-complexity of
![]() ${\mathit{sim}_{5}}$
, where the dots show the intersections of the costs of the decision trees.
${\mathit{sim}_{5}}$
, where the dots show the intersections of the costs of the decision trees.
4.2 Level-p-complexity for
 ${\mathit{maj}_{3}^2}$
${\mathit{maj}_{3}^2}$
When running
![]() ${\mathit{genAlgThinMemo}\;\mathrm{9}\;\mathit{maj}_{3}^2} we get {\{\mskip1.5mu \mathit{P}\;[\mskip1.5mu \mathrm{4},\mathrm{4},\mathrm{6},\mathrm{9},\mathbin{-}\mathrm{61},\mathrm{23},\mathrm{67},\mathbin{-}\mathrm{64},\mathrm{16}\mskip1.5mu]\mskip1.5mu\}}$
, which means that the expected cost (
${\mathit{genAlgThinMemo}\;\mathrm{9}\;\mathit{maj}_{3}^2} we get {\{\mskip1.5mu \mathit{P}\;[\mskip1.5mu \mathrm{4},\mathrm{4},\mathrm{6},\mathrm{9},\mathbin{-}\mathrm{61},\mathrm{23},\mathrm{67},\mathbin{-}\mathrm{64},\mathrm{16}\mskip1.5mu]\mskip1.5mu\}}$
, which means that the expected cost (
![]() $P_*$
) of the best decision tree (
$P_*$
) of the best decision tree (
![]() ${{\mathit{T}_{*}}}$
) is
${{\mathit{T}_{*}}}$
) is
This can be compared to the decision tree (that we call
![]() ${{\mathit{T}_{\mathit{t}}}}$
) conjectured in Jansson (Reference Jansson2022) to be the best. Its expected cost is slightly higher (thus worse):
${{\mathit{T}_{\mathit{t}}}}$
) conjectured in Jansson (Reference Jansson2022) to be the best. Its expected cost is slightly higher (thus worse):
The expected costs for decision trees
![]() ${{\mathit{T}_{*}}}$
and
${{\mathit{T}_{*}}}$
and
![]() ${{\mathit{T}_{\mathit{t}}}}$
was shown already in Figure 2. Comparing the two polynomials using
${{\mathit{T}_{\mathit{t}}}}$
was shown already in Figure 2. Comparing the two polynomials using
![]() ${\mathit{cmpPoly}\;{\mathit{P}_{*}}\;{\mathit{P}_{\mathit{t}}}}$
shows that the new one has strictly lower expected cost than the one from the thesis. The difference, illustrated in Figure 3, factors to exactly and we note that it is non-negative in the whole interval.
${\mathit{cmpPoly}\;{\mathit{P}_{*}}\;{\mathit{P}_{\mathit{t}}}}$
shows that the new one has strictly lower expected cost than the one from the thesis. The difference, illustrated in Figure 3, factors to exactly and we note that it is non-negative in the whole interval.
The value of the polynomials at the endpoints is 4, and the maximum of
![]() ${{\mathit{P}_{*}}}$
is
${{\mathit{P}_{*}}}$
is
![]() $\approx6.14$
compared to the maximum of
$\approx6.14$
compared to the maximum of
![]() ${{\mathit{P}_{\mathit{t}}}}$
which is
${{\mathit{P}_{\mathit{t}}}}$
which is
![]() $\approx6.19$
. The conjecture in Jansson (Reference Jansson2022), is thus false and the correct formula for the level-p-complexity of
$\approx6.19$
. The conjecture in Jansson (Reference Jansson2022), is thus false and the correct formula for the level-p-complexity of
![]() ${\mathit{maj}_{3}^2} is {{\mathit{P}_{*}}}$
. At the time of publication of Jansson (Reference Jansson2022) it was believed that sifting through all the possible decision trees would be intractable. Fortunately, using a combination of thinning, memoization, and exact comparison of polynomials, it is now possible to compute the correct complexity in less than a second on the author’s laptop.
${\mathit{maj}_{3}^2} is {{\mathit{P}_{*}}}$
. At the time of publication of Jansson (Reference Jansson2022) it was believed that sifting through all the possible decision trees would be intractable. Fortunately, using a combination of thinning, memoization, and exact comparison of polynomials, it is now possible to compute the correct complexity in less than a second on the author’s laptop.
5 Conclusions
This paper describes a Haskell library for computing level-p-complexity of Boolean functions and applies it to two-level iterated majority
![]() $({\mathit{maj}_{3}^2})$
. The problem specification is straightforward: generate all possible decision trees, compute their expected cost polynomials, and select the best ones. The implementation is more of a challenge because of two sources of exponential computational cost: an exponential growth in the set of decision trees and an exponential growth in the size of the recursive call graph (the collection of subfunctions). The library uses thinning to tackle the first and memoization to handle the second source of inefficiency. In combination with efficient data structures (binary decision diagrams for the Boolean function input, sets of polynomials for the output), this enables computing the level-
$({\mathit{maj}_{3}^2})$
. The problem specification is straightforward: generate all possible decision trees, compute their expected cost polynomials, and select the best ones. The implementation is more of a challenge because of two sources of exponential computational cost: an exponential growth in the set of decision trees and an exponential growth in the size of the recursive call graph (the collection of subfunctions). The library uses thinning to tackle the first and memoization to handle the second source of inefficiency. In combination with efficient data structures (binary decision diagrams for the Boolean function input, sets of polynomials for the output), this enables computing the level-
![]() ${\mathit{p}}$
-complexity for our target example
${\mathit{p}}$
-complexity for our target example
![]() ${\mathit{maj}_{3}^2}$
in less than a second.
${\mathit{maj}_{3}^2}$
in less than a second.
From the mathematics point of view, the strength of the methods used in this paper to compute the level-
![]() ${\mathit{p}}$
-complexity is that we can get a correct result to something which is very hard to calculate by hand. From a computer science point of view, the paper is an instructive example of how a combination of algorithmic and symbolic tools can tame a doubly exponential computational cost.
${\mathit{p}}$
-complexity is that we can get a correct result to something which is very hard to calculate by hand. From a computer science point of view, the paper is an instructive example of how a combination of algorithmic and symbolic tools can tame a doubly exponential computational cost.
The library uses type classes for separation of concerns: the actual implementation type for Boolean functions (the input) is abstracted over by the
![]() ${\mathit{BoFun}}$
class; and the corresponding type for the output is modeled by the
${\mathit{BoFun}}$
class; and the corresponding type for the output is modeled by the
![]() ${\mathit{TreeAlg}}$
class. We also use our own class
${\mathit{TreeAlg}}$
class. We also use our own class
![]() ${\mathit{Thinnable}}$
for thinning (and preorders) and the
${\mathit{Thinnable}}$
for thinning (and preorders) and the
![]() ${\mathit{Memoizable}}$
class from hackage. This means that our main function has the following type:
${\mathit{Memoizable}}$
class from hackage. This means that our main function has the following type:
All the Haskell code is available on GitHub Footnote 7 , and parts of it has been reproduced in Agda to check some of the stronger invariants. One direction of future work is to complete the Agda formalization so that we can provide a formally verified library, perhaps helped by Swierstra (Reference Swierstra2022); van der Rest & Swierstra (Reference van der Rest and Swierstra2022).
The set of polynomials we compute are all incomparable in the preorder and, together with the thinning relation this means that we actually compute what is called a Pareto front from economics: a set of solutions where no objective can be improved without sacrificing at least one other objective. It would be interesting to explore this in more detail and to see what the overlap is between thinning as an algorithm design method and different concepts of optimality from economics.
The computed level-p-complexity for
![]() ${\mathit{maj}_{3}^2}$
is better than the result conjectured in Jansson (Reference Jansson2022), and the library allows easy exploration of other Boolean functions. With the current library, the level-
${\mathit{maj}_{3}^2}$
is better than the result conjectured in Jansson (Reference Jansson2022), and the library allows easy exploration of other Boolean functions. With the current library, the level-
![]() ${\mathit{p}}$
-complexity of iterated majority on 3 levels (27 bits) is out of reach, but with Christian Sattler and Liam Hughes we are exploring a version specialized to “iterated threshold functions” which can handle this case (see code in the GitHub repository).
${\mathit{p}}$
-complexity of iterated majority on 3 levels (27 bits) is out of reach, but with Christian Sattler and Liam Hughes we are exploring a version specialized to “iterated threshold functions” which can handle this case (see code in the GitHub repository).
Acknowledgments
The authors would like to extend their gratitude to Jeffrey Steif for the idea of exploring level-
![]() ${\mathit{p}}$
-complexity and for supervising the preceding work, reported in Jansson (Reference Jansson2022). Further, we would like to thank Tim Richter and Jeremy Gibbons for taking their time to give valuable feedback on the first draft of this paper. The authors thank the JFP editors and reviewers, whose helpful and constructive comments have lead to significant improvements of the original manuscript. The work presented in this paper heavily relies on free software, among others on GHC, Agda, Haskell, git, Emacs, LaTeX and on the Ubuntu operating system, Mathematica, and Visual Studio Code. It is our pleasure to thank all developers of these excellent products.
${\mathit{p}}$
-complexity and for supervising the preceding work, reported in Jansson (Reference Jansson2022). Further, we would like to thank Tim Richter and Jeremy Gibbons for taking their time to give valuable feedback on the first draft of this paper. The authors thank the JFP editors and reviewers, whose helpful and constructive comments have lead to significant improvements of the original manuscript. The work presented in this paper heavily relies on free software, among others on GHC, Agda, Haskell, git, Emacs, LaTeX and on the Ubuntu operating system, Mathematica, and Visual Studio Code. It is our pleasure to thank all developers of these excellent products.
Conflicts of Interest
None.




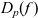
































Discussions
No Discussions have been published for this article.