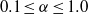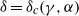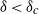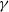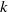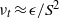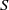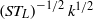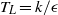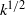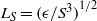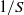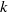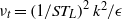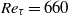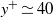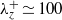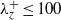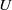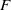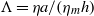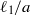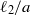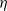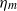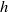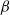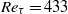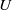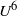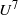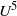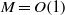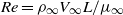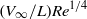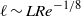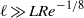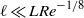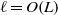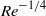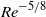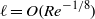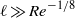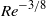Papers
Experimental study of parametric subharmonic instability for internal plane waves
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 1-20
-
- Article
- Export citation
Low-Reynolds-number flow through two-dimensional shunts
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 21-39
-
- Article
- Export citation
Quasi-geostrophic shallow-water doubly-connected vortex equilibria and their stability
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 40-68
-
- Article
- Export citation
Coarsening and solidification via solvent-annealing in thin liquid films
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 69-90
-
- Article
- Export citation
An explicit algebraic Reynolds-stress and scalar-flux model for stably stratified flows
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 91-125
-
- Article
- Export citation
Some insights for the prediction of near-wall turbulence
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 126-139
-
- Article
- Export citation
Lagrangian approach to laminar–turbulent interfaces in transitional pipe flow
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 140-162
-
- Article
- Export citation
A spherical squirming swimmer in unsteady Stokes flow
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 163-189
-
- Article
- Export citation
Solution of the quasi-one-dimensional linearized Euler equations using flow invariants and the Magnus expansion
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 190-231
-
- Article
- Export citation
Worst-case amplification of disturbances in inertialess Couette flow of viscoelastic fluids
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 232-263
-
- Article
- Export citation
Near-wall turbulent fluctuations in the absence of wide outer motions
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 264-288
-
- Article
- Export citation
Multilayer shallow water equations with complete Coriolis force. Part 3. Hyperbolicity and stability under shear
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 289-317
-
- Article
- Export citation
Turbulent boundary-layer noise: direct radiation at Mach number 0.5
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 318-351
-
- Article
- Export citation
Diffusion in hydrogel-supported phospholipid bilayer membranes
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 352-373
-
- Article
- Export citation
The quasi-geostrophic theory of the thermal shallow water equations
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 374-403
-
- Article
- Export citation
Large-eddy simulation of passive scalar dispersion in an urban-like canopy
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 404-428
-
- Article
- Export citation
Wall turbulence without walls
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 429-455
-
- Article
- Export citation
Aerodynamic noise from a poroelastic edge with implications for the silent flight of owls
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 456-479
-
- Article
- Export citation
Receptivity of the boundary layer to vibrations of the wing surface
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 480-528
-
- Article
- Export citation
On the problem of large-scale magnetic field generation in rotating compressible convection
-
- Published online by Cambridge University Press:
- 16 April 2013, pp. 529-555
-
- Article
- Export citation