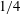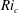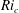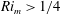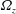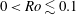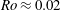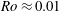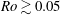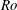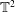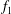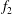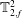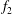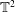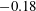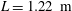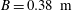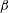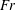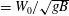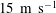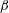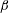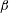JFM Perspectives
The reciprocal theorem in fluid dynamics and transport phenomena
-
- Published online by Cambridge University Press:
- 30 September 2019, P1
-
- Article
- Export citation
JFM Rapids
Kelvin–Helmholtz billows above Richardson number
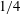 $1/4$
$1/4$
-
- Published online by Cambridge University Press:
- 23 September 2019, R1
-
- Article
- Export citation
JFM Papers
Koopman mode expansions between simple invariant solutions
-
- Published online by Cambridge University Press:
- 19 September 2019, pp. 1-27
-
- Article
- Export citation
Fast equilibration dynamics of viscous particle-laden flow in an inclined channel
-
- Published online by Cambridge University Press:
- 19 September 2019, pp. 28-53
-
- Article
- Export citation
D’Yakov–Kontorovich instability in planar reactive shocks
-
- Published online by Cambridge University Press:
- 19 September 2019, pp. 54-84
-
- Article
- Export citation
Propagation speed of inertial waves in cylindrical swirling flows
-
- Published online by Cambridge University Press:
- 19 September 2019, pp. 85-120
-
- Article
- Export citation
The hydrodynamic lift of a slender, neutrally buoyant fibre in a wall-bounded shear flow at small Reynolds number
-
- Published online by Cambridge University Press:
- 19 September 2019, pp. 121-146
-
- Article
- Export citation
On the origin of the drag force on dimpled spheres
-
- Published online by Cambridge University Press:
- 20 September 2019, pp. 147-167
-
- Article
- Export citation
Experimental study of particle trajectories below deep-water surface gravity wave groups
-
- Published online by Cambridge University Press:
- 20 September 2019, pp. 168-186
-
- Article
- Export citation
Behaviour of small-scale turbulence in the turbulent/non-turbulent interface region of developing turbulent jets
-
- Published online by Cambridge University Press:
- 20 September 2019, pp. 187-216
-
- Article
- Export citation
Data-driven prediction of unsteady flow over a circular cylinder using deep learning
-
- Published online by Cambridge University Press:
- 23 September 2019, pp. 217-254
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale interactions in turbulent rotating planar Couette flow: insight through the Reynolds stress transport
-
- Published online by Cambridge University Press:
- 26 September 2019, pp. 255-295
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental study of the nonlinear saturation of the elliptical instability: inertial wave turbulence versus geostrophic turbulence
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 296-326
-
- Article
- Export citation
Thermodynamically consistent modelling of two-phase flows with moving contact line and soluble surfactants
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 327-359
-
- Article
- Export citation
Comprehensive shear stress analysis of turbulent boundary layer profiles
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 360-389
-
- Article
-
- You have access
- HTML
- Export citation
Forced synchronization of quasiperiodic oscillations in a thermoacoustic system
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 390-421
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faraday instability of a liquid layer on a lubrication film
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 422-447
-
- Article
- Export citation
Richtmyer–Meshkov instability of an unperturbed interface subjected to a diffracted convergent shock
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 448-467
-
- Article
- Export citation
The controlled vertical impact of an inclined flat plate on a quiescent water surface
-
- Published online by Cambridge University Press:
- 27 September 2019, pp. 468-511
-
- Article
- Export citation
Langmuir turbulence and filament frontogenesis in the oceanic surface boundary layer
-
- Published online by Cambridge University Press:
- 01 October 2019, pp. 512-553
-
- Article
- Export citation