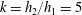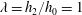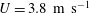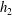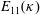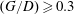Focus on Fluids
Footprints of a flapping wing
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
From red cells to soft lubrication, an experimental study of lift generation inside a compressible porous layer
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 5-25
-
- Article
- Export citation
Rough-wall turbulent boundary layers with constant skin friction
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 26-45
-
- Article
- Export citation
Convection from a line-source into a two-layer stratified ambient fluid
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 46-67
-
- Article
- Export citation
Dynamics of a small gap gas lubricated bearing with Navier slip boundary conditions
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 68-99
-
- Article
- Export citation
Dynamics of an elastic sphere containing a thin creeping region and immersed in an acoustic region for similar viscous-elastic and acoustic time and length scales
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 100-115
-
- Article
- Export citation
Size and shape of shock waves and slipline for Mach reflection in steady flow
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 116-140
-
- Article
- Export citation
The topology of gas jets injected beneath a surface and subject to liquid cross-flow
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 141-183
-
- Article
- Export citation
Normalized dissipation rate in a moderate Taylor Reynolds number flow
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 184-204
-
- Article
- Export citation
Spin-down in a rapidly rotating cylinder container with mixed rigid and stress-free boundary conditions
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 205-240
-
- Article
- Export citation
Complex solutions of the Dean equations and non-uniqueness at all Reynolds numbers
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 241-259
-
- Article
- Export citation
Three-dimensional wake transition for a circular cylinder near a moving wall
-
- Published online by Cambridge University Press:
- 05 April 2017, pp. 260-287
-
- Article
- Export citation
On the non-parallel instability of the rotating-sphere boundary layer
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 288-318
-
- Article
- Export citation
Short-wavelength local instabilities of a circular Couette flow with radial temperature gradient
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 319-343
-
- Article
- Export citation
Euler and Navier–Stokes equations in a new time-dependent helically symmetric system: derivation of the fundamental system and new conservation laws
-
- Published online by Cambridge University Press:
- 31 March 2017, pp. 344-365
-
- Article
- Export citation
Local flow characterization using bioinspired sensory information
-
- Published online by Cambridge University Press:
- 31 March 2017, pp. 366-381
-
- Article
- Export citation
Unsteadily manipulating internal flow barriers
-
- Published online by Cambridge University Press:
- 04 April 2017, pp. 382-406
-
- Article
- Export citation
Hydrodynamic force on a sphere normal to an obstacle due to a non-uniform flow
-
- Published online by Cambridge University Press:
- 04 April 2017, pp. 407-434
-
- Article
- Export citation
Performance and mechanism of sinusoidal leading edge serrations for the reduction of turbulence–aerofoil interaction noise
-
- Published online by Cambridge University Press:
- 04 April 2017, pp. 435-464
-
- Article
- Export citation
Direct numerical simulation of triboelectric charging in particle-laden turbulent channel flows
-
- Published online by Cambridge University Press:
- 05 April 2017, pp. 465-491
-
- Article
- Export citation