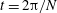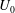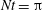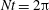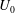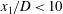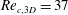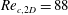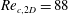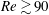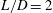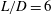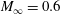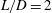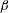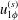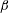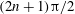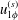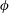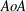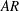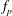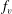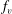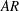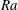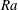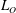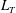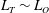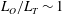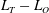Focus on Fluids
Ultrasound rays in droplets: the role of viscosity and caustics in acoustic streaming
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Direct numerical simulation of stratified flow past a sphere at a subcritical Reynolds number of 3700 and moderate Froude number
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 5-31
-
- Article
- Export citation
Two- and three-dimensional wake transitions of an impulsively started uniformly rolling circular cylinder
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 32-59
-
- Article
- Export citation
The excitation of Görtler vortices by free stream coherent structures
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 60-96
-
- Article
- Export citation
Non-wetting impact of a sphere onto a bath and its application to bouncing droplets
-
- Published online by Cambridge University Press:
- 02 August 2017, pp. 97-127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability of two-layer Couette flows
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 128-157
-
- Article
- Export citation
Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 158-204
-
- Article
- Export citation
On the noise prediction for serrated leading edges
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 205-234
-
- Article
- Export citation
Initial development of a free-surface wall jet at moderate Reynolds number
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 235-269
-
- Article
- Export citation
Biglobal instabilities of compressible open-cavity flows
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 270-301
-
- Article
- Export citation
Topology of three-dimensional steady cellular flow in a two-sided anti-parallel lid-driven cavity
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 302-334
-
- Article
- Export citation
Oscillatory and streaming flow between two spheres due to combined oscillations
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 335-362
-
- Article
- Export citation
Passive pitching of splitters in the trailing edge of elliptic cylinders
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 363-375
-
- Article
- Export citation
Stability of plane Poiseuille–Couette flow in a fluid layer overlying a porous layer
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 376-395
-
- Article
- Export citation
Asymptotically based self-similarity solution of the Navier–Stokes equations for a porous tube with a non-circular cross-section
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. 396-420
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simulation of turbulent boundary layer wall pressure fluctuations via Poisson equation and synthetic turbulence
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 421-454
-
- Article
- Export citation
Self-similar rupture of thin films of power-law fluids on a substrate
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 455-483
-
- Article
- Export citation
Onset of convection induced by centrifugal buoyancy in a rotating cavity
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 484-502
-
- Article
- Export citation
Harmonics generation and the mechanics of saturation in flow over an open cavity: a second-order self-consistent description
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 503-521
-
- Article
- Export citation
Role of overturns in optimal mixing in stratified mixing layers
-
- Published online by Cambridge University Press:
- 08 August 2017, pp. 522-552
-
- Article
- Export citation