Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-27T07:33:51.069Z Has data issue: false hasContentIssue false
  • English
  • Français

A weakly nonlinear mechanism for mode selection in swirling jets

Published online by Cambridge University Press:  16 April 2012

Philippe Meliga ,
François Gallaire  and
Jean-Marc Chomaz
Philippe Meliga*
Affiliation:
M2P2, CNRS-Universités d’Aix-Marseille, 13451 Marseilles, France
François Gallaire
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH1015 Lausanne, Switzerland
Jean-Marc Chomaz
Affiliation:
LadHyX, CNRS-École Polytechnique, 91128 Palaiseau, France
*
†Email address for correspondence: philippe.meliga@l3m.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

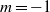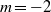Global linear and nonlinear bifurcation analysis is used to revisit the spiral vortex breakdown of nominally axisymmetric swirling jets. For the parameters considered herein, stability analyses single out two unstable linear modes of azimuthal wavenumber and , bifurcating from the axisymmetric breakdown solution. These modes are interpreted in terms of spiral perturbations wrapped around and behind the axisymmetric bubble, rotating in time in the same direction as the swirling flow but winding in space in the opposite direction. Issues are addressed regarding the role of these modes with respect to the existence, mode selection and internal structure of vortex breakdown, as assessed from the three-dimensional direct numerical simulations of Ruith et al. (J. Fluid Mech., vol. 486, 2003, pp. 331–378). The normal form describing the leading-order nonlinear interaction between modes is computed and analysed. It admits two stable solutions corresponding to pure single and double helices. At large swirl, the axisymmetric solution bifurcates to the double helix which remains the only stable solution. At low and moderate swirl, it bifurcates first to the single helix, and subsequently to the double helix through a series of subcritical bifurcations yielding hysteresis over a finite range of Reynolds numbers, the estimated bifurcation threshold being in good agreement with that observed in the direct numerical simulations. Evidence is provided that this selection is not to be ascribed to classical mean flow corrections induced by the existence of the unstable modes, but to a non-trivial competition between harmonics. Because the frequencies of the leading modes approach a strong 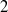: 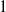resonance, an alternative normal form allowing interactions between the 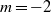mode and the first harmonics of the 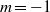mode is computed and analysed. It admits two stable solutions, the double helix already identified in the non-resonant case, and a single helix differing from that observed in the non-resonant case only by the presence of a slaved, phase-locked harmonic deformation. On behalf of the finite departure from the 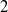: resonance, the amplitude of the slaved harmonic is however low, and the effect of the resonance on the bifurcation structure is merely limited to a reduction of the hysteresis range.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Pattern formation Vortex Flows: Vortex breakdown
Type
Papers
Information
Journal of Fluid Mechanics , Volume 699 , 25 May 2012 , pp. 216 - 262
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abshagen, J., Lopez, J. M., Marques, F. & Pfister, G. 2005 Mode competition of rotating waves in reflection-symmetric Taylor–Couette flow. J. Fluid Mech. 540, 269–299.Google Scholar
2. Avila, M., Meseguer, A. & Marques, F. 2006 Double hopf bifurcation in corotating spiral Poiseuille flow. Phys. Fluids 18 (064101), 1–13.CrossRefGoogle Scholar
3. Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.CrossRefGoogle Scholar
4. Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
5. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
6. Davis, T. A. 2004 A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw. 30 (2), 165–195 available online from http://www.cise.ufl.edu/research/sparse/umfpack/.CrossRefGoogle Scholar
7. Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute/convective instabilities in the batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
8. Doedel, E. J., Champneys, A. R., Fairgrieve, T. F., Kuznetsov, Y. A., Sandstede, B. & Wang, X. 1997Auto 97: continuation and bifurcation software for ordinary differential equations (with HomCont), Users Guide, available online from http://indy.cs.concordia.ca/auto/.Google Scholar
9. Escudier, M. 1988 Vortex breakdown: observations and explanations. Prog. Aerosp. Sci. 25, 189–229.Google Scholar
10. Escudier, M., Bornstein, J. & Maxworthy, T. 1982 The dynamics of confined vortices. Proc. R. Soc. Lond. A 382, 335–360.Google Scholar
11. Escudier, M. & Zehnder, N. 1982 Vortex-flow regimes. J. Fluid Mech. 115, 105–121.Google Scholar
12. Faler, J. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20, 1385–1400.CrossRefGoogle Scholar
13. Friedrichs, K. O. 1973 Spectral Theory of Operators in Hilbert Space. Springer.Google Scholar
14. Gallaire, F. & Chomaz, J.-M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.Google Scholar
15. Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
16. Grabowski, W. & Berger, S. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75, 535–544.CrossRefGoogle Scholar
17. Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer.CrossRefGoogle Scholar
18. Hall, M. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.Google Scholar
19. Hecht, F., Pironneau, O., Morice, J., Le Hyaric, A. & Ohtsuka, K. 2011 Freefem++ Manual, 3rd edn. available online from http://www.freefem.org/ff++/.Google Scholar
20. Herrada, M. A. & Fernandez-Feria, R. 2006 On the development of three-dimensional vortex breakdown in cylindrical regions. Phys. Fluids 18 (084105), 1–15.Google Scholar
21. Huerre, P. 2000 Open shear flow instabilities. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G. ). pp. 159–229. Cambridge University Press.Google Scholar
22. Knobloch, E. & Proctor, M. R. E. 1988 The double Hopf bifurcation with 2:1 resonance. Proc. R. Soc. Lond. A 415, 61–90.Google Scholar
23. Kuznetsov, Y. A. 1998 Elements of Applied Bifurcation Theory, 2nd edn. Springer.Google Scholar
24. Lambourne, N. C. & Bryer, D. W. 1961 The bursting of leading-edge vortices: some observations and discussion of the phenomenon. Aero. Res. Counc. R&M 3282.Google Scholar
25. LeBlanc, V. G. & Langford, W. F. 1996 Classification and unfoldings of 1:2 resonant hopf bifurcation. Arch. Rat. Mech. Anal. 136, 305–357.Google Scholar
26. Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM, available online from http://www.caam.rice.edu/software/ARPACK/.Google Scholar
27. Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.CrossRefGoogle Scholar
28. Lim, D. & Redekopp, L. 1998 Absolute instability conditions for variable density, swirling jet flows. Eur. J. Mech. (B/Fluids) 17, 165–185.Google Scholar
29. Loiseleux, T., Chomaz, J.-M. & Huerre, P. 1998 The effect of swirl on jets and wakes: linear instability of the Rankine vortex with axial flow. Phys. Fluids 10, 1120–1134.Google Scholar
30. Lopez, J. M. 2006 Rotating and modulated rotating waves in transitions of an enclosed swirling flow. J. Fluid Mech. 553, 323–346.Google Scholar
31. Marques, F., Gelfgat, A. Yu. & Lopez, J. M. 2003 Tangent double hopf bifurcation in a differentially rotating cylinder flow. Phys. Rev. E 68 (016310), 1–13.CrossRefGoogle Scholar
32. Marques, F., Lopez, J. M. & Shen, J. 2002 Mode interactions in an enclosed swirling flow: a double hopf bifurcation between azimuthal wavenumbers 0 and 2. J. Fluid Mech. 455, 263–281.Google Scholar
33. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of the cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
34. Meliga, P., Chomaz, J.-M. & Sipp, D. 2009 Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.Google Scholar
35. Meliga, P. & Gallaire, F. 2011 Control of axisymmetric vortex breakdown in a constricted pipe: nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 23 (084102), 1–23.Google Scholar
36. Nore, C., Moisy, F. & Quartier, L. 2005 Experimental observation of near-heteroclinic cycles in the von Kármán swirling flow. Phys. Fluids 17 (064103), 1–10.CrossRefGoogle Scholar
37. Nore, C., Tuckerman, L. S., Daube, O. & Xin, S. 2003 The 1:2 mode interaction in exactly counter-rotating von Kármán swirling flow. J. Fluid Mech. 477, 51–88.CrossRefGoogle Scholar
38. Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.CrossRefGoogle Scholar
39. Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
40. Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
41. Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.CrossRefGoogle Scholar
42. Spall, R. E. & Gatski, T. B. 1991 A computational study of the topology of vortex breadkown. Proc. R. Soc. Lond. A 435, 321–337.Google Scholar
43. Tuckerman, L. S. 2001 Thermosolutal and binary fluid convection as a matrix problem. Physica D 156, 325–363.Google Scholar

Meliga et al. supplementary material

Movie 1: animated stable simple helix at Re = 120, S = 1.3. Numerically computed dye lines transported from t=0 up to t = 70 by the second-order analytic solution reconstructed from the asymptotic expansion. The movie has been obtained by initially releasing particles

Download Meliga et al. supplementary material(Video)
Video 3.4 MB

Meliga et al. supplementary material

Movie 1: animated stable simple helix at Re = 120, S = 1.3. Numerically computed dye lines transported from t=0 up to t = 70 by the second-order analytic solution reconstructed from the asymptotic expansion. The movie has been obtained by initially releasing particles

Download Meliga et al. supplementary material(Video)
Video 7.7 MB

Meliga et al. supplementary material

Movie 2: same as movie 1 for the stable double helix at Re=150, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 3.4 MB

Meliga et al. supplementary material

Movie 2: same as movie 1 for the stable double helix at Re=150, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 7.6 MB

Meliga et al. supplementary material

Movie 3: same as movie 1 for the unstable T2-torus at Re=120, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 3.4 MB

Meliga et al. supplementary material

Movie 3: same as movie 1 for the unstable T2-torus at Re=120, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 7.6 MB

Meliga et al. supplementary material

Movie 4: same as movie 1 for the stable mixed-modes solution at Re=120, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 3.8 MB

Meliga et al. supplementary material

Movie 4: same as movie 1 for the stable mixed-modes solution at Re=120, S=1.3.

Download Meliga et al. supplementary material(Video)
Video 9.8 MB