Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T22:53:24.025Z Has data issue: false hasContentIssue false
  • English
  • Français

A unified criterion for the centrifugal instabilities of vortices and swirling jets

Published online by Cambridge University Press:  01 October 2013

Paul Billant  and
François Gallaire
Paul Billant*
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
François Gallaire
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, School of Engineering, EPFL, 1015 Lausanne, Switzerland
*
†Email address for correspondence: billant@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Swirling jets and vortices can both be unstable to the centrifugal instability but with a different wavenumber selection: the most unstable perturbations for swirling jets in inviscid fluids have an infinite azimuthal wavenumber, whereas, for vortices, they are axisymmetric but with an infinite axial wavenumber. Accordingly, sufficient condition for instability in inviscid fluids have been derived asymptotically in the limits of large azimuthal wavenumber 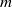$m$ for swirling jets (Leibovich and Stewartson, J. Fluid Mech., vol. 126, 1983, pp. 335–356) and large dimensionless axial wavenumber 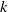$k$ for vortices (Billant and Gallaire, J. Fluid Mech., vol. 542, 2005, pp. 365–379). In this paper, we derive a unified criterion valid whatever the magnitude of the axial flow by performing an asymptotic analysis for large total wavenumber 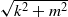$ \sqrt{{k}^{2} + {m}^{2} } $. The new criterion recovers the criterion of Billant and Gallaire when the axial flow is small and the Leibovich and Stewartson criterion when the axial flow is finite and its profile sufficiently different from the angular velocity profile. When the latter condition is not satisfied, it is shown that the accuracy of the Leibovich and Stewartson asymptotics is strongly reduced. The unified criterion is validated by comparisons with numerical stability analyses of various classes of swirling jet profiles. In the case of the Batchelor vortex, it provides accurate predictions over a wider range of axial wavenumbers than the Leibovich–Stewartson criterion. The criterion shows also that a whole range of azimuthal wavenumbers are destabilized as soon as a small axial velocity component is present in a centrifugally unstable vortex.

JFM classification

Instability: Instability Wakes/Jets: Jets Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 734 , 10 November 2013 , pp. 5 - 35
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, L1–L4.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Carton, X. & McWilliams, J. C. 1989 Barotropic and baroclinic instabilities of axisymmetric vortices in a quasi-geostrophic model. In Mesoscale/Synoptic Coherent Structures in Geophysical Turbulence (ed. Nihoul, J. & Jamart, B.), pp. 225–244. Elsevier.Google Scholar
Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute/convective instabilities in the Batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
Delbende, I. & Rossi, M. 2005 Nonlinear evolution of a swirling jet instability. Phys. Fluids 17, 044103.Google Scholar
Di Pierro, B. & Abid, M. 2010 Instabilities of variable-density swirling flows. Phys. Rev. E 82, 046312.CrossRefGoogle ScholarPubMed
Di Pierro, B. & Abid, M. 2012 Rayleigh–Taylor instability in variable density swirling flows. Eur. Phys. J. B 85, 1–8.Google Scholar
Duck, P. W. & Foster, M. R. 1980 The inviscid stability of a trailing line vortex. Z. Angew. Math. Phys. 31, 524–532.CrossRefGoogle Scholar
Eckhoff, K. S. 1984 A note on the instability of columnar vortices. J. Fluid Mech. 145, 417–421.CrossRefGoogle Scholar
Eckhoff, K. S. & Storesletten, L. 1978 A note on the stability of steady inviscid helical gas flows. J. Fluid Mech. 89, 401–411.Google Scholar
Emanuel, K. A. 1984 A note on the stability of columnar vortices. J. Fluid Mech. 145, 235–238.Google Scholar
Fabre, D. & Jacquin, L. 2004 Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.Google Scholar
Fabre, D. & Le Dizès, S. 2008 Viscous and inviscid centre modes in the linear stability of vortices: the vicinity of the neutral curves. J. Fluid Mech. 603, 1–38.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.CrossRefGoogle Scholar
Heading, J. 1962 An introduction to phase-integral methods. John Wiley & Sons.Google Scholar
Heaton, C. J. 2007a Centre modes in inviscid swirling flows and their application to the stability of the Batchelor vortex. J. Fluid Mech. 576, 325–348.Google Scholar
Heaton, C. J. 2007b Optimal growth of the Batchelor vortex viscous modes. J. Fluid Mech. 592, 495–505.Google Scholar
Heaton, C. J. & Peake, N. 2006 Algebraic and exponential instability of inviscid swirling flow. J. Fluid Mech. 565, 279–318.Google Scholar
Heaton, C. J. & Peake, N. 2007 Transient growth in vortices with axial flow. J. Fluid Mech. 587, 271–301.CrossRefGoogle Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14, 463–476.Google Scholar
Khorrami, M. R. 1991 On the viscous modes of instability of a trailing line vortex. J. Fluid Mech. 225, 197–212.Google Scholar
Le Dizès, S. & Fabre, D. 2007 Large-Reynolds-number asymptotic analysis of viscous centre modes in vortices. J. Fluid Mech. 585, 153–180.Google Scholar
Le Dizès, S. & Fabre, D. 2010 Viscous ring modes in vortices with axial jet. Theor. Comput. Fluid Dyn. 24, 349–361.Google Scholar
Leblanc, S. & Le Duc, A. 2005 The unstable spectrum of swirling gas flows. J. Fluid Mech. 537, 433–442.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Lessen, M. & Paillet, F. 1974 Stability of a trailing line vortex. Part 2. Viscous theory. J. Fluid Mech. 65, 769–779.CrossRefGoogle Scholar
Lessen, M., Singh, P. J. & Paillet, F. 1974 Stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.Google Scholar
Ludwieg, H. 1960 Stabilität der strömung in einem zylindrischen ringraum. Z. Flugwiss. 8, 135–140.Google Scholar
Mayer, E. W. & Powell, K. G. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.Google Scholar
Müller, S. 2007 Numerical investigations of compressible turbulent swirling jet flows. PhD thesis, Swiss Federal Institute of Technology Zürich.Google Scholar
Müller, S. B. & Kleiser, L. 2008 Viscous and inviscid spatial stability analysis of compressible swirling mixing layers. Phys. Fluids 20, 114103.Google Scholar
Olendraru, C. & Sellier, A. 2002 Viscous effects in the absolute-convective instability of the Batchelor vortex. J. Fluid Mech. 459, 371–396.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Schiff, L. I. 1968 Quantum Mechanics, 3rd edn. McGraw-Hill.Google Scholar
Sipp, D., Fabre, D., Michelin, S. & Jacquin, L. 2005 Stability of a vortex with a heavy core. J. Fluid Mech. 526, 67–76.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11, 305–322.Google Scholar
Stewartson, K. & Brown, S. N. 1985 Near-neutral centre-modes as inviscid perturbations to a trailing line vortex. J. Fluid Mech. 156, 387–399.Google Scholar
Stewartson, K. & Capell, K. 1985 On the stability of ring modes in a trailing line vortex – the upper neutral points. J. Fluid Mech. 156, 369–386.Google Scholar
Stewartson, K & Leibovich, S. 1987 On the stability of a columnar vortex to disturbances with large azimuthal wavenumber – the lower neutral points. J. Fluid Mech. 178, 549–566.Google Scholar
Sun, D.-J., Hu, G.-H., Gao, Z. & Yin, X.-Y. 2002 Stability and temporal evolution of a swirling jet with centrifugally unstable azimuthal velocity. Phys. Fluids 14, 4081–4084.Google Scholar
Synge, J. L. 1933 The stability of heterogeneous liquids. Trans. R. Soc. Can. 27, 1–18.Google Scholar