Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-10T23:03:09.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Stokes flow of vesicles in a circular tube

Published online by Cambridge University Press:  30 July 2018

Joseph M. Barakat Open the ORCID record for Joseph M. Barakat [Opens in a new window]  and
Eric S. G. Shaqfeh
Joseph M. Barakat
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA
Eric S. G. Shaqfeh*
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA Institute for Computational and Mathematical Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: esgs@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The inertialess motion of lipid-bilayer vesicles flowing through a circular tube is investigated via direct numerical simulation and lubrication theory. A fully three-dimensional boundary integral equation method, previously used to study unbounded and wall-bounded Stokes flows around freely suspended vesicles, is extended to study the hindered mobility of vesicles through conduits of arbitrary cross-section. This study focuses on the motion of a periodic train of vesicles positioned concentrically inside a circular tube, with particular attention given to the effects of tube confinement, vesicle deformation and membrane bending elasticity. When the tube diameter is comparable to the transverse dimension of the vesicle, axisymmetric lubrication theory provides an approximate solution to the full Stokes-flow problem. By combining the present numerical results with a previously reported asymptotic theory (Barakat & Shaqfeh, J. Fluid Mech., vol. 835, 2018, pp. 721–761), useful correlations are developed for the vesicle velocity 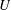$U$ and extra pressure drop 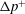$\unicode[STIX]{x0394}p^{+}$. When bending elasticity is relatively weak, these correlations are solely functions of the geometry of the system (independent of the imposed flow rate). The prediction of Barakat & Shaqfeh (2018) supplies the correct limiting behaviour of 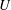$U$ and 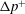$\unicode[STIX]{x0394}p^{+}$ near maximal confinement, whereas the present study extends this result to all regimes of confinement. Vesicle–vesicle interactions, shape transitions induced by symmetry breaking, and unsteadiness introduce quantitative changes to 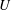$U$ and 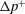$\unicode[STIX]{x0394}p^{+}$. By contrast, membrane bending elasticity can qualitatively affect the hydrodynamics at sufficiently low flow rates. The dependence of 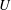$U$ and 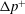$\unicode[STIX]{x0394}p^{+}$ on the membrane bending stiffness (relative to a characteristic viscous stress scale) is found to be rather complex. In particular, the competition between viscous forces and bending forces can hinder or enhance the vesicle’s mobility, depending on the geometry and flow conditions.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Biological Fluid Dynamics: Capsule/cell dynamics Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 606 - 635
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aouane, O., Farutin, A., Thiébaud, M., Benyoussef, A., Wagner, C. & Misbah, C. 2017 Hydrodynamic pairing of soft particles in a confined flow. Phys. Rev. Fluids 2 (6), 063102.Google Scholar
Aouane, O., Thiebaud, M., Benyoussef, A., Wagner, C. & Misbah, C. 2014 Vesicle dynamics in a confined Poiseuille flow: from steady-state to chaos. Phys. Rev. E 90 (3), 033011.Google Scholar
Bagchi, P. & Kalluri, R. M. 2010 Rheology of a dilute suspension of liquid-filled elastic capsules. Phys. Rev. E 81 (5), 056320.Google Scholar
Bagchi, P. & Kalluri, R. M. 2011 Dynamic rheology of a dilute suspension of elastic capsules: effect of capsule tank-treading, swinging and tumbling. J. Fluid Mech. 669, 498–526.Google Scholar
Barakat, J. M. & Shaqfeh, E. S. G. 2018 The steady motion of a closely fitting vesicle in a tube. J. Fluid Mech. 835, 721–761.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Brenner, H. 1970 Pressure drop due to the motion of neutrally buoyant particles in duct flows. J. Fluid Mech 43 (4), 641–660.Google Scholar
Brenner, H. & Happel, J. 1958 Slow viscous flow past a sphere in a cylindrical tube. J. Fluid Mech. 4 (2), 195–213.Google Scholar
Chen, T. C. & Skalak, R. 1970 Stokes flow in a cylindrical tube containing a line of spheroidal particles. Appl. Sci. Res. 22 (1), 403–441.Google Scholar
Coupier, G., Farutin, A., Minetti, C., Podgorski, T. & Misbah, C. 2012 Shape diagram of vesicles in Poiseuille flow. Phys. Rev. Lett. 108 (1), 178106.Google Scholar
Danker, G., Biben, T., Podgorski, T., Verdier, C. & Misbah, C. 2007 Dynamics and rheology of a dilute suspension of vesicles: higher-order theory. Phys. Rev. E 76 (4), 041905.Google Scholar
Danker, G., Vlahovska, P. M. & Misbah, C. 2009 Vesicles in Poiseuille flow. Phys. Rev. Lett. 102 (14), 148102.Google Scholar
Deschamps, J., Kantsler, V. & Steinberg, V. 2009 Phase diagram of single vesicle dynamical states in shear flow. Phys. Rev. Lett. 102 (11), 118105.Google Scholar
Duffy, M. G. 1982 Quadrature over a pyramid or cube of integrands with a singularity at a vertex. SIAM J. Numer. Anal. 19 (6), 1260–1262.Google Scholar
Farutin, A. & Misbah, C. 2011 Symmetry breaking of vesicle shapes in Poiseuille flow. Phys. Rev. E 84 (1), 011902.Google Scholar
Farutin, A. & Misbah, C. 2012 Squaring, parity breaking, and S tumbling of vesicles under shear flow. Phys. Rev. Lett. 109 (24), 248106.Google Scholar
Farutin, A. & Misbah, C. 2014 Symmetry breaking and cross-streamline migration of three-dimensional vesicles in an axial Poiseuille flow. Phys. Rev. E 89 (4), 042709.Google Scholar
Frost, P. A. & Harper, E. Y. 1976 An extended Padé procedure for constructing global approximations from asymptotic expansions: an explication with examples. SIAM Rev. 18 (1), 62–91.Google Scholar
Guckenberger, A., Schraml, M. P., Chen, P. G., Leonetti, M. & Gekle, S. 2016 On the bending algorithms for soft objects in flows. Comput. Phys. Commun. 207, 1–23.Google Scholar
Halpern, D. & Secomb, T. W. 1989 The squeezing of red blood cells through capillaries with near-minimal diameters. J. Fluid Mech. 203, 381–400.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (2), 317–328.Google Scholar
Helfrich, W. 1973 Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28c (11), 693–703.Google Scholar
Hochmuth, R. M. & Sutera, S. P. 1970 Spherical caps in low Reynolds-number tube flow. Chem. Engng Sci. 25 (4), 593–604.Google Scholar
Janssen, P. J. A., Baron, M. D., Anderson, P. D., Blawzdziewicz, J., Loewenberg, M. & Wajnryb, E. 2012 Collective dynamics of confined rigid spheres and deformable drops. Soft Matt. 8 (28), 7495–7506.Google Scholar
Jenkins, J. T. 1977 Static equilibrium configurations of a model red blood cell. J. Math. Biol. 4 (2), 149–169.Google Scholar
Kantsler, V., Segre, E. & Steinberg, V. 2008a Critical dynamics of vesicle stretching transition in elongational flow. Phys. Rev. Lett. 101 (4), 048101.Google Scholar
Kantsler, V., Segre, E. & Steinberg, V. 2008b Dynamics of interacting vesicles and rheology of vesicle suspension in shear flow. Europhys. Lett. 82 (5), 58005.Google Scholar
Kantsler, V. & Steinberg, V. 2006 Transition to tumbling and two regimes of tumbling motion of a vesicle in shear flow. Phys. Rev. Lett. 96 (3), 036001.Google Scholar
Kaoui, B., Tahiri, N., Biben, T., Ez-Zahraouy, H., Benyoussef, A., Biros, G. & Misbah, C. 2011 Complexity of vesicle microcirculation. Phys. Rev. E 84 (4), 041906.Google Scholar
Knoll, D. A. & Keys, D. E. 2004 Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193 (2), 357–397.Google Scholar
Kreyszig, E. 1959 Differential Geometry. Dover.Google Scholar
Liron, N. & Mochon, S. 1976 Stokes flow for a Stokeslet between two parallel flat plates. J. Engng Maths 10, 287–303.Google Scholar
Liron, N. & Shahar, R. 1978 Stokes flow due to a Stokeslet in a pipe. J. Fluid Mech. 86, 727–744.Google Scholar
Loewenberg, M. & Hinch, E. J. 1996 Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 321, 395–419.Google Scholar
Loop, C. T.1987 smooth subdivision surfaces based on triangles. PhD thesis, University of Utah.Google Scholar
Misbah, C. 2006 Vacillating breathing and tumbling of vesicles under shear flow. Phys. Rev. Lett. 96 (2), 028104.Google Scholar
Morrison, D. D., Riley, J. D. & Zancanaro, J. F. 1962 Multiple shooting method for two-point boundary value problems. Commun. ACM 5 (12), 613–614.Google Scholar
Narsimhan, V., Spann, A. P. & Shaqfeh, E. S. G. 2014 The mechanism of shape instability for a vesicle in extensional flow. J. Fluid Mech. 750, 144–190.Google Scholar
Narsimhan, V., Spann, A. P. & Shaqfeh, E. S. G. 2015 Pearling, wrinkling, and buckling of vesicles in elongational flows. J. Fluid Mech. 777, 1–26.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Ratulowski, J. & Chang, H. C. 1989 Transport of gas bubbles in capillaries. Phys. Fluids A 1 (1), 1642–1655.Google Scholar
Saintillan, D., Darve, E. & Shaqfeh, E. S. G. 2005 A smooth particle-mesh Ewald algorithm for Stokes suspension simulations: the sedimentation of fibers. Phys. Fluids 17 (3), 3301.Google Scholar
Secomb, T. W. 1988 Interaction between bending and tension forces in bilayer membranes. Biophys. J. 54 (4), 743–746.Google Scholar
Secomb, T. W., Skalak, R., Oozkaya, N. & Gross, J. F. 1986 Flow of axisymmetric red blood cells in narrow capillaries. J. Fluid Mech. 163, 405–423.Google Scholar
Seifert, U., Berndl, K. & Lipowsky, R. 1991 Shape transformations of vesicles: phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A 44 (2), 1182–1202.Google Scholar
Sonshine, R. M. & Brenner, H. 1966 The stokes translation of two or more particles along the axis of an infinitely long circular cylinder. Appl. Sci. Res. 16 (1), 425–454.Google Scholar
Spann, A. P., Zhao, H. & Shaqfeh, E. S. G. 2014 Loop subdivision surface boundary integral method simulations of vesicles at low reduced volume ratio in shear and extensional flow. Phys. Fluids 26 (3), 031902.Google Scholar
Stoer, J. & Bulirsch, R. 2002 Introduction to Numerical Analysis, 3rd edn, vol. 12. Springer.Google Scholar
Thiebaud, M. & Misbah, C. 2013 Rheology of a vesicle suspension with finite concentration: a numerical study. Phys. Rev. E 88 (6), 062707.Google Scholar
Tözeren, H. 1984 Boundary integral equation method for some Stokes problems. Intl J. Numer. Meth. Fluids 4 (2), 159–170.Google Scholar
Trozzo, R., Boedec, G., Leonetti, M. & Jaeger, M. 2015 Axisymmetric boundary element method for vesicles in a capillary. J. Comput. Phys. 289, 62–82.Google Scholar
Vitkova, V., Mader, M. & Podgorski, T. 2004 Deformation of vesicles flowing through capillaries. Europhys. Lett. 68 (3), 398–404.Google Scholar
Vitkova, V., Mader, M. A., Polack, B., Misbah, C. & Podgorski, T. 2008 Micro-macro link in rheology of erythrocyte and vesicle suspensions. Biophys. J. 95 (6), L33–L35.Google Scholar
Vlahovska, P. M. & Gracia, R. S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75 (1), 016313.Google Scholar
Wakiya, S. 1957 Viscous flows past a spheroid. J. Phys. Soc. Japan 12 (10), 1130–1141.Google Scholar
Wang, H. & Skalak, R. 1969 Viscous flow in a cylindrical tube containing a line of spherical particles. J. Fluid Mech. 38, 75–96.Google Scholar
Youngren, G. K. & Acrivos, A. 1975 Stokes flow past a particle of arbitrary shape: a numerical method of solution. J. Fluid Mech. 69 (2), 377–403.Google Scholar
Zhao, H., Isfahani, A. H. G., Olson, L. N. & Freund, J. B. 2010 A spectral boundary integral method for flowing blood cells. J. Comput. Phys. 229 (1), 3726–3744.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2011 The dynamics of a vesicle in simple shear flow. J. Fluid Mech. 674, 578–604.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2013a The dynamics of a non-dilute vesicle suspension in a simple shear flow. J. Fluid Mech. 725, 709–731.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2013b The shape stability of a lipid vesicle in a uniaxial extensional flow. J. Fluid Mech. 719, 345–361.Google Scholar
Zhao, H., Shaqfeh, E. S. G. & Narsimhan, V. 2012 Shear-induced particle migration and margination in a cellular suspension. Phys. Fluids 24 (1), 011902.Google Scholar
Zhao, H., Spann, A. P. & Shaqfeh, E. S. G. 2011 The dynamics of a vesicle in a wall-bound shear flow. Phys. Fluids 23 (12), 121901.Google Scholar
Zhong-can, O.-Y. & Helfrich, W. 1989 Bending energy of vesicle membranes: general expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Phys. Rev. A 39 (10), 5280–5288.Google Scholar