Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-30T17:44:49.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady Rayleigh–Bénard convection between stress-free boundaries

Published online by Cambridge University Press:  04 November 2020

Baole Wen Open the ORCID record for Baole Wen [Opens in a new window] ,
David Goluskin Open the ORCID record for David Goluskin [Opens in a new window] ,
Matthew LeDuc ,
Gregory P. Chini Open the ORCID record for Gregory P. Chini [Opens in a new window]  and
Charles R. Doering Open the ORCID record for Charles R. Doering [Opens in a new window]
Baole Wen*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI48109-1043, USA
David Goluskin
Affiliation:
Department of Mathematics & Statistics, University of Victoria, Victoria, BCV8P 5C2, Canada
Matthew LeDuc
Affiliation:
Department of Physics, University of Michigan, Ann Arbor, MI48109-1040, USA
Gregory P. Chini
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH03824, USA Department of Mechanical Engineering, University of New Hampshire, Durham, NH03824, USA
Charles R. Doering
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI48109-1043, USA Department of Physics, University of Michigan, Ann Arbor, MI48109-1040, USA Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI48109-1042, USA
*
†Email address for correspondence: baolew@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

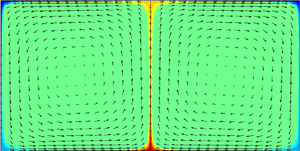
Steady two-dimensional Rayleigh–Bénard convection between stress-free isothermal boundaries is studied via numerical computations. We explore properties of steady convective rolls with aspect ratios ${\rm \pi} /5\leqslant \varGamma \leqslant 4{\rm \pi}$, where $\varGamma$ is the width-to-height ratio for a pair of counter-rotating rolls, over eight orders of magnitude in the Rayleigh number, $10^3\leqslant Ra\leqslant 10^{11}$, and four orders of magnitude in the Prandtl number, $10^{-2}\leqslant Pr\leqslant 10^2$. At large $Ra$ where steady rolls are dynamically unstable, the computed rolls display $Ra \rightarrow \infty$ asymptotic scaling. In this regime, the Nusselt number $Nu$ that measures heat transport scales as $Ra^{1/3}$ uniformly in $Pr$. The prefactor of this scaling depends on $\varGamma$ and is largest at $\varGamma \approx 1.9$. The Reynolds number $Re$ for large-$Ra$ rolls scales as $Pr^{-1} Ra^{2/3}$ with a prefactor that is largest at $\varGamma \approx 4.5$. All of these large-$Ra$ features agree quantitatively with the semi-analytical asymptotic solutions constructed by Chini & Cox (Phys. Fluids, vol. 21, 2009, 083603). Convergence of $Nu$ and $Re$ to their asymptotic scalings occurs more slowly when $Pr$ is larger and when $\varGamma$ is smaller.

Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 905 , 25 December 2020 , R4
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.CrossRefGoogle ScholarPubMed
Chini, G. P. & Cox, S. M. 2009 Large Rayleigh number thermal convection: heat flux predictions and strongly nonlinear solutions. Phys. Fluids 21, 083603.CrossRefGoogle Scholar
Doering, C. R. 2020 Turning up the heat in turbulent thermal convection. Proc. Natl Acad. Sci. 117, 9671–9673.CrossRefGoogle ScholarPubMed
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53, 5957–5981.CrossRefGoogle ScholarPubMed
Goluskin, D. 2015 Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Goluskin, D., Johnston, H., Flierl, G. R. & Spiegel, E. A. 2014 Convectively driven shear and decreased heat flux. J. Fluid Mech. 759, 360–385.CrossRefGoogle Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54, 34–39.CrossRefGoogle Scholar
Lorenz, E. N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141.2.0.CO;2>CrossRefGoogle Scholar
Malkus, W. V. R. & Veronis, G. 1958 Finite amplitude cellular convection. J. Fluid Mech. 4, 225–260.CrossRefGoogle Scholar
Newell, A. C. & Whitehead, J. A. 1969 Finite bandwidth, finite amplitude convection. J. Fluid Mech. 38, 279–303.CrossRefGoogle Scholar
Pandey, A., Verma, M. K. & Mishra, P. K. 2014 Scaling of heat flux and energy spectrum for very large Prandtl number convection. Phys. Rev. E 89, 023006.CrossRefGoogle ScholarPubMed
Pandey, A. & Verma, M. K. 2016 Scaling of large-scale quantities in Rayleigh–Bénard convection. Phys. Fluids 28, 095105.CrossRefGoogle Scholar
Pandey, A., Verma, M. K., Chatterjee, A. G. & Dutta, B. 2016 Similarities between 2D and 3D convection for large Prandtl number. Pramana-J. Phys. 87, 13.CrossRefGoogle Scholar
Paul, S., Verma, M. K., Wahi, P., Reddy, S. K. & Kumar, K. 2012 Bifurcation analysis of the flow patterns in two-dimensional Rayleigh–Bénard convection. Intl J. Bifurcation Chaos 22, 1230018.CrossRefGoogle Scholar
Petschel, K., Stellmach, S., Wilczek, M., Lülff, J. & Hansen, U. 2013 Dissipation layers in Rayleigh–Bénard convection: a unifying view. Phys. Rev. Lett. 110, 114502.CrossRefGoogle ScholarPubMed
van der Poel, E. P., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2014 Effect of velocity boundary conditions on the heat transfer and flow topology in two-dimensional Rayleigh–Bénard convection. Phys. Rev. E 90, 013017.CrossRefGoogle ScholarPubMed
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.CrossRefGoogle Scholar
Robinson, J. L. 1967 Finite amplitude convection cells. J. Fluid Mech. 30, 577–600.CrossRefGoogle Scholar
Sondak, D., Smith, L. M. & Waleffe, F. 2015 Optimal heat transport solutions for Rayleigh–Bénard convection. J. Fluid Mech. 784, 565–595.CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Trefethen, L. N. & Bau III, D. 1997 Numerical Linear Algebra. SIAM.CrossRefGoogle Scholar
Waleffe, F., Boonkasame, A. & Smith, L. M. 2015 Heat transport by coherent Rayleigh–Bénard convection. Phys. Fluids 27, 051702.CrossRefGoogle Scholar
Wang, Q., Chong, K.-L., Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2020 From zonal flow to convection rolls in Rayleigh–Bénard convection with free-slip plates. arXiv:2005.02084.CrossRefGoogle Scholar
Wen, B. & Chini, G. P. 2018 Inclined porous medium convection at large Rayleigh number. J. Fluid Mech. 837, 670–702.CrossRefGoogle Scholar
Wen, B., Chini, G. P., Kerswell, R. R. & Doering, C. R. 2015 a Time-stepping approach for solving upper-bound problems: application to two-dimensional Rayleigh–Bénard convection. Phys. Rev. E 92, 043012.CrossRefGoogle ScholarPubMed
Wen, B., Corson, L. T. & Chini, G. P. 2015 b Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid. Mech. 772, 197–224.CrossRefGoogle Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106, 244501.CrossRefGoogle ScholarPubMed
Supplementary material: File

Wen et al. supplementary material

Wen et al. supplementary material

Download Wen et al. supplementary material(File)
File 73.2 KB