No CrossRef data available.
Article contents
Standing waves, localised near the shoreline of a water basin, and asymptotic quasimodes
Published online by Cambridge University Press: 31 May 2024
Abstract
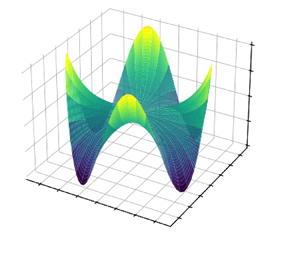
In this work, formal asymptotic solutions of a problem for linear water waves in a bounded basin are constructed. The solutions have the form of asymptotic quasimodes and are used for the description of standing water waves localised near the shoreline. Such short-wavelength quasimodes exist only for a discrete set of frequencies, which are determined by means of a quantisation-type condition. Some numerical results are also addressed.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Anikin, A., Dobrohotov, S., Nazaykinsky, V. & Tsvetkova, A. 2019 Asymptotics of the eigenfunctions of the operator 
$\boldsymbol {\nabla } D(x)\boldsymbol {\nabla }$ in 2D domains degenerating on their boundaries and billiards with semi-rigid walls. Differ. Equ. 55 (5), 660–672.Google Scholar
$\boldsymbol {\nabla } D(x)\boldsymbol {\nabla }$ in 2D domains degenerating on their boundaries and billiards with semi-rigid walls. Differ. Equ. 55 (5), 660–672.Google ScholarBabich, V. & Buldyrev, V. 1991 Short-Wavelength Diffraction Theory. Springer Series on Wave Phenomena. Springer.Google Scholar
Dobrohotov, S. 1986 Asymptotic behaviour of water surface waves trapped by shores and irregularities of the bottom relief. Sov. Phys. Dokl. 31 (7), 537–539.Google Scholar
Dobrohotov, S., Zhevandrov, P. & Simonov, K. 1985 Stokes edge waves in closed aqua-basins. In Theoretical and Experimental Studies of Long-Wave Processes, pp. 13–19. FESC, USSR Academy of Sciences (in Russian).Google Scholar
Dobrokhotov, S., Minenkov, D. & Votiakova, M. 2024 Asymptotics of long nonlinear coastal waves in basins with gentle shores. Russ. J. Math. Phys. 31 (1), 79–93.Google Scholar
Evans, D.V. 1989 Edge waves over a sloping beach. Q. J. Mech. Appl. Maths 42, 131–142.CrossRefGoogle Scholar
Huntley, D., Guza, R. & Thornton, E. 1981 Field observations of surf beat. 1. Progressive edge waves. J. Geophys. Res. 86 (C7), 6451–6466.Google Scholar
Kuznetsov, N., Maz'ya, V. & Vainberg, B. 2002 Linear Water Waves. Cambridge University Press.CrossRefGoogle Scholar
Lazutkin, V.F. 1993 KAM Theory and Semiclassical Approximations to Eigenfunctions. Springer.Google Scholar
Liu, X. & Wang, X. 2023 Polygonal patterns of Faraday water waves analogous to collective excitations in Bose–Einstein condensates. Nat. Phys. 20, 287–293.Google Scholar
Lyalinov, M.A. 2021 A comment on eigenfunctions and eigenvalues of the Laplace operator in an angle with robin boundary conditions. J. Math. Sci. 252, 646–653.Google Scholar
Lyalinov, M.A. 2023 Localized waves propagating along an angular junction of two thin semi-infinite elastic membranes terminating an acoustic medium. Russ. J. Math. Phys. 30 (3), 345–359.CrossRefGoogle Scholar
Rockliff, N. 1978 Finite amplitude effects in free and forced edge waves. Proc. Camb. Phil. Soc. 83, 463–479.CrossRefGoogle Scholar
Roseau, M. 1958 Short waves parallel to the shore over a sloping beach. Commun. Pure Appl. Maths 11, 433–493.CrossRefGoogle Scholar
Stokes, G.G. 1846 Report on recent researches in hydrodynamics. In Report of the 16th Meeting of the British Association for the Advancement of Science, Southampton, pp. 1–20. John Murray.Google Scholar
Ursell, F. 1952 Edge waves on a sloping beach. Proc. R. Soc. Lond. A 214 (1116), 79–97.Google Scholar
Yeh, Y. 1986 Experimental study of standing edge waves. J. Fluid Mech. 169, 291–304.CrossRefGoogle Scholar